圆的认识课件

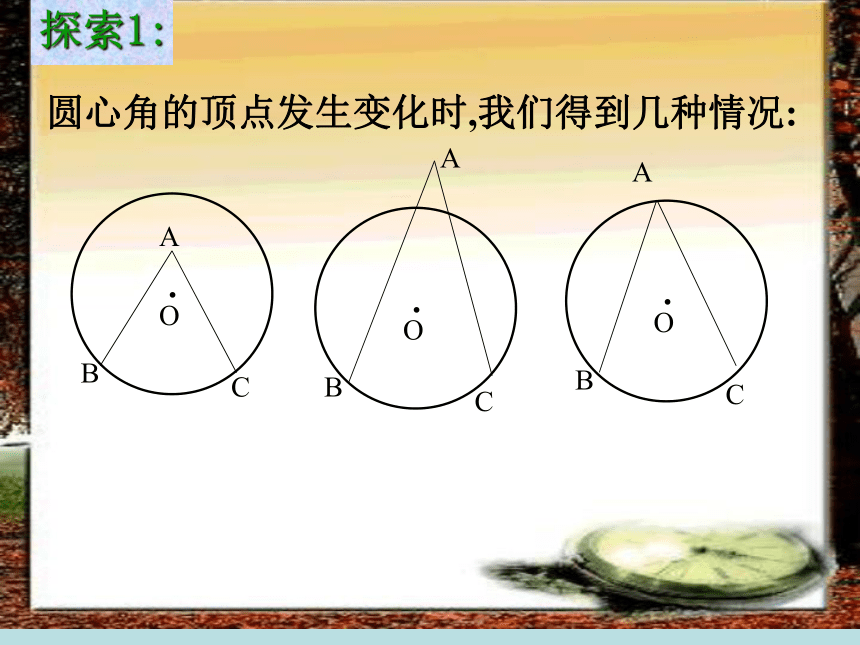
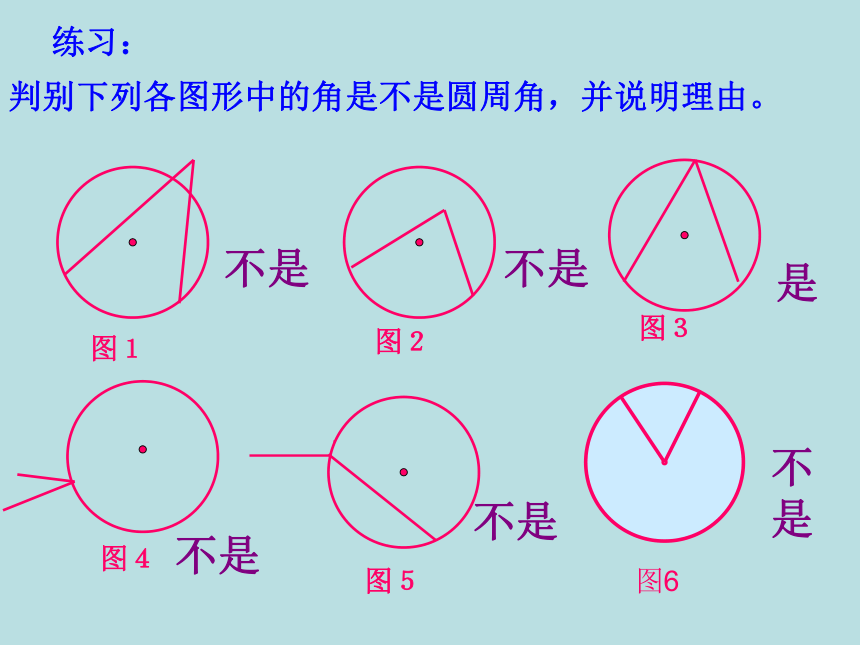
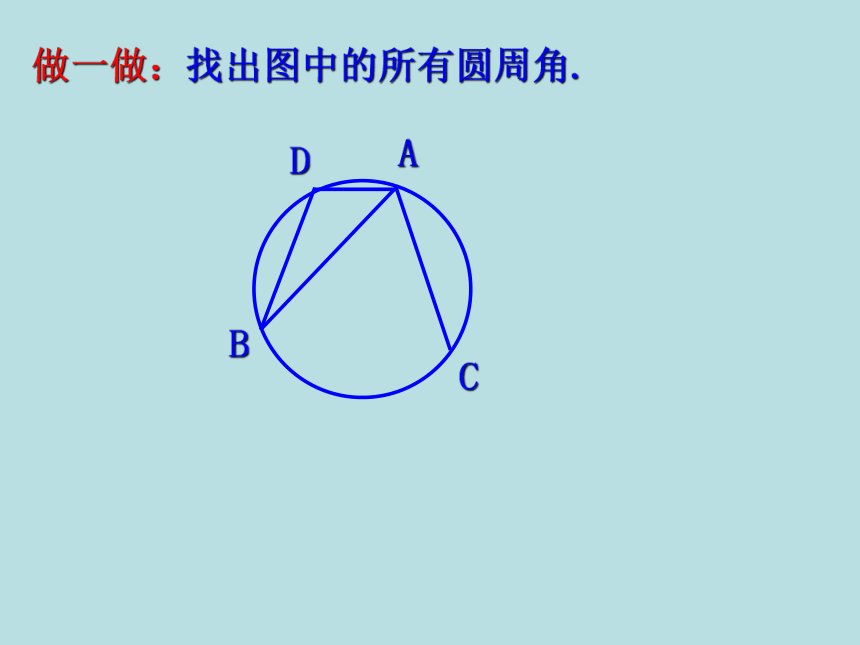
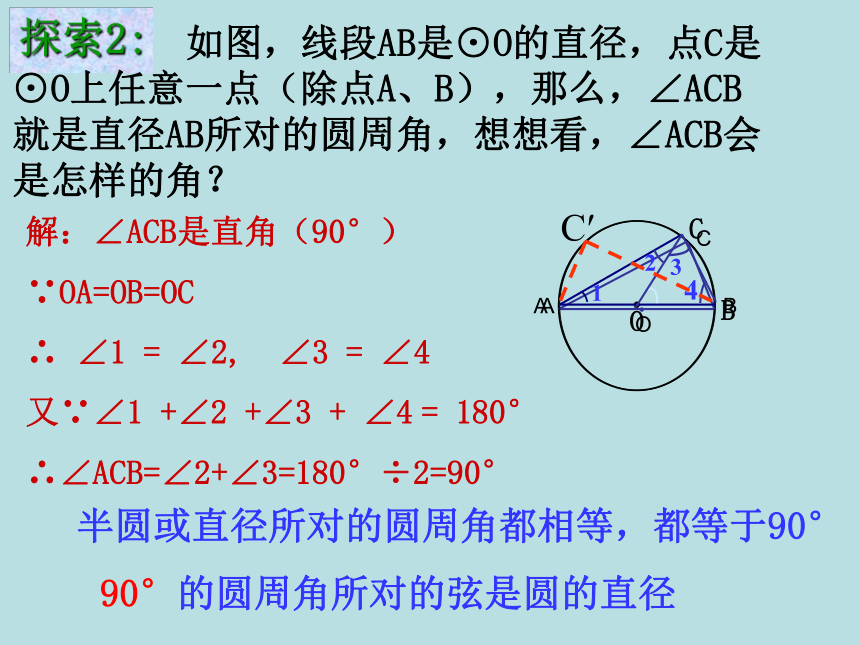
课件20张PPT。OABC圆周角和圆心角的关系中英文学校1.圆心角的定义顶点在圆心的角叫圆心角.忆一忆圆心角的顶点发生变化时,我们得到几种情况:.探索1:观察图中的∠ABC ,你能仿照圆心角的定义给它下个定义吗?⑵角的两边分别和圆相交●特征：⑴顶点在圆上●●顶点在圆上,并且两边都和圆相交的角叫圆周角.练习：判别下列各图形中的角是不是圆周角，并说明理由。不是不是是不是不是图１图２图３图４图５图6不是做一做：找出图中的所有圆周角.探索2: 如图，线段AB是⊙O的直径，点C是⊙O上任意一点（除点A、B），那么，∠ACB就是直径AB所对的圆周角，想想看，∠ACB会是怎样的角？解：∠ACB是直角（90°）
∵OA=OB=OC
∴ ∠1 = ∠2, ∠3 = ∠4
又∵∠1 +∠2 +∠3 + ∠4 = 180°
∴∠ACB=∠2+∠3=180°÷2=90°半圆或直径所对的圆周角都相等，都等于90°90°的圆周角所对的弦是圆的直径C′应用举例解 例　如图，AB是⊙O的直径，∠A=80°．
求∠ABC的度数． ∵AB是⊙O的直径
∴ ∠ACB＝90°(直径所对的圆周角是直角) ∴ ∠ABC＝180°－∠A－∠ACB
　　　＝180°－80°－90°
＝10° ∵ ∠A=80°探索3: 思考：半圆所对的圆周角与它所对的圆心角有关系吗？讨论：对于一般的弧所对的圆周角，是否也有这样的规律呢？同一条弧所对的圆周角会等于圆心角的一半∵ ∠ACB＝90°∠AOB＝180°已知,在⊙O中, BC所对的圆周角是∠BAC,所对的圆心角是∠BOC证明:∵ OA=OC
∴ ∠C=∠BAC
∵∠BOC=∠BAC+∠C∴ ∠AOC =2 ∠ABO一条弧所对的圆周角等于它所对的圆心角的一半.（2）若圆心在∠BAC的内部.证明:作直径AD.利用(1)的结论可知结论 在同圆(或等圆)中，同弧或等弧所对的圆周角等于该弧所对的圆心角的一半；结论：在同圆(或等圆)中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧相等。
练习:130°例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABC例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABCD1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.2.半圆或直径所对的圆周角都相等，都等于90°
90°的圆周角所对的弦是圆的直径小结:3.在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。小结:再见谢谢指导