有理数的乘法
图片预览






文档简介
课件18张PPT。1.4.1 有理数的乘法温故而知新:1.把下列各式写成省略加号的和的形式:
( +12) – ( - 18) + ( - 7) – ( +15)
(2) (- 1.6) + ( - ) – (+3.14) – (-1.732)12 + 18 - 7 –15
- 1.6 - – 3.14 +1.732
2.|+2|= |+3|= |-2|=
|-3|= |9|= |- |=232393.若蜗牛向右爬行2 cm记为+2 cm,那么
它向左爬行2 cm记为 .-2 cm 若3分钟后记为+3分,那么3分钟
前记为_____. -3分4.如果蜗牛一直以每分2cm的速度向前爬行,3分钟它走了多远?
解:2×3 = 6 (cm)预习了吗?评价一下!(- 1)×5 = (-3)×(-8) =
(-9)×0 = (+6)×0 = 提出问题:若蜗牛向右爬行2 cm记为+2 cm,那么它向左爬行2 cm记为-2cm.若3分钟后记为+3分,那么3分钟前记为-3分.1.如果蜗牛一直以每分2cm的速度向右爬行,3分后它在什么位置?0246(1) (+2)(蜗牛现在的位置在O点)×(+3)= + 62.如果蜗牛一直以每分2cm的速度向左爬行,
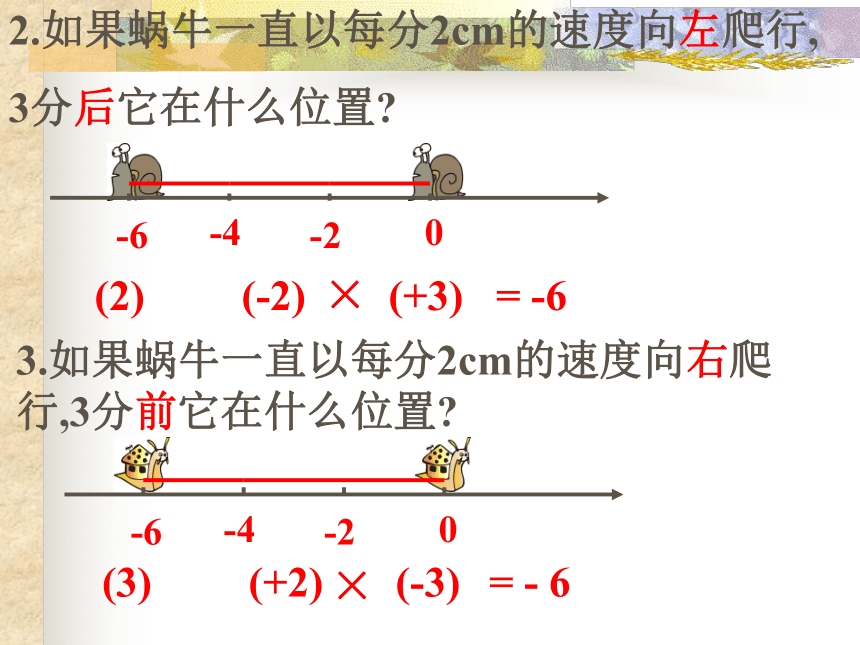
3分后它在什么位置?
0-2-4-6(2) (-2)3.如果蜗牛一直以每分2cm的速度向右爬行,3分前它在什么位置?
0-2-4-6(3) (+2)×(+3)= -6×(-3)= - 64.如果蜗牛一直以每分2cm的速度向左爬行,3分前它在什么位置?
6420(4) (-2)
×(- 3)= +6探索规律:(1) (+2)×(+3) = +6
(2) (-2)×(+3) = - 6
(3) (+2)×(-3) = - 6
(4) (-2)×(-3) = + 6(同学们讨论)正数乘以正数积为 数, 负数乘以正数积为 数,
正数乘以负数积为 数, 负数乘以负数积为 数,
乘积的绝对值等于各乘数绝对值的 。正正负负积你可以规纳了吗? 两数相乘,同号得正,异号得负,并把绝对值相乘。
任何一个数同0相乘,都得0。与有理数加法法则一样,先确定符号,再确定绝对值。例如:(-5)×(-3)解:原式=+同号两数相乘得正=15把绝对值相乘(-7)×4解:原式=-异号两数相乘得负= -28把绝对值相乘有理数乘法法则:(5×3)(7×4)再如: (- )×(-2)解:原式= ×2
= 1有理数中仍有:乘积是1的两个数互为倒数.如: -的倒数是-2, -2的倒数是-同学们说说下列各数的倒数:1, -1 , 5, -5 ,0有倒数吗?
倒数是它本身的数有 个,分别是 .
数a(a≠0)的倒数是 .0没有倒数.21和-1预习了吗?评价一下!(- 1)×5 = (-3)×(-8) =
(-9)×0 = (+6)×0 = -52400你可以计算了吗?1.计算:(口答) (-3)×9 (2) 6×(-9) (3) (-4)×6
(4) (-6)×(-1) (5) (-6)×0 (6) ×(- )
2.用正负数表示气温的变化量,上升为正,下降为负,登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?解: (-6)×3 = - 18℃
答:气温下降18℃.=-27=-54=-24=6=03.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?解: (-5)×60 = - 300(元)
答:销售额下降了300元.4.计算下列各题:
(1) (-8)×(-7) (2) 2.9×(-0.4)
(3) 100×(-0.001) (4) ×开拓视野:一、选择题:
1、一个有理数与它的相反数的积是( )
A、一定小于0 B、一定大于0
C、一定不小于0 D、一定不大于0
2、有两个有理数a、b, ab>0,a + b<0.则( )
A、a>0, b>0 B、a<0, b<0
C、a>0, b<0 D、a<0, b>0
3、如果ab=0,那么一定有( )
A、a=b=0 B、a=0
C、a,b至少有一个为0 D、 a,b最多有一个为0
DBC二、从七张标有5、3、1、0、-2、-4、-6的卡片中取出3张卡片,使这3张卡片上的数字乘积是最大,应抽哪3张?使积最小呢?解:积最大的3张是:5、-4、-6
5×(-4)×(-6) = 120积最小的3张是:5、3、-6
5×3×(-6) = -90小结:1.两数相乘,同号得正,异号得负,并把 绝对值相乘。
任何一个数同0相乘,都得0。2.有理数中仍有:乘积是1的两个数互为倒数. 0没有倒数。3.数a(a≠0)的倒数是作业:1、复习本节内容第34页至37页。
2、课外作业:课本第47页
第1题(2)、(4)、(6)
第2题全部
第3题(2)、(4)、(6)
3、预习第37、38页。谢谢各位老师的指导
再 见
( +12) – ( - 18) + ( - 7) – ( +15)
(2) (- 1.6) + ( - ) – (+3.14) – (-1.732)12 + 18 - 7 –15
- 1.6 - – 3.14 +1.732
2.|+2|= |+3|= |-2|=
|-3|= |9|= |- |=232393.若蜗牛向右爬行2 cm记为+2 cm,那么
它向左爬行2 cm记为 .-2 cm 若3分钟后记为+3分,那么3分钟
前记为_____. -3分4.如果蜗牛一直以每分2cm的速度向前爬行,3分钟它走了多远?
解:2×3 = 6 (cm)预习了吗?评价一下!(- 1)×5 = (-3)×(-8) =
(-9)×0 = (+6)×0 = 提出问题:若蜗牛向右爬行2 cm记为+2 cm,那么它向左爬行2 cm记为-2cm.若3分钟后记为+3分,那么3分钟前记为-3分.1.如果蜗牛一直以每分2cm的速度向右爬行,3分后它在什么位置?0246(1) (+2)(蜗牛现在的位置在O点)×(+3)= + 62.如果蜗牛一直以每分2cm的速度向左爬行,
3分后它在什么位置?
0-2-4-6(2) (-2)3.如果蜗牛一直以每分2cm的速度向右爬行,3分前它在什么位置?
0-2-4-6(3) (+2)×(+3)= -6×(-3)= - 64.如果蜗牛一直以每分2cm的速度向左爬行,3分前它在什么位置?
6420(4) (-2)
×(- 3)= +6探索规律:(1) (+2)×(+3) = +6
(2) (-2)×(+3) = - 6
(3) (+2)×(-3) = - 6
(4) (-2)×(-3) = + 6(同学们讨论)正数乘以正数积为 数, 负数乘以正数积为 数,
正数乘以负数积为 数, 负数乘以负数积为 数,
乘积的绝对值等于各乘数绝对值的 。正正负负积你可以规纳了吗? 两数相乘,同号得正,异号得负,并把绝对值相乘。
任何一个数同0相乘,都得0。与有理数加法法则一样,先确定符号,再确定绝对值。例如:(-5)×(-3)解:原式=+同号两数相乘得正=15把绝对值相乘(-7)×4解:原式=-异号两数相乘得负= -28把绝对值相乘有理数乘法法则:(5×3)(7×4)再如: (- )×(-2)解:原式= ×2
= 1有理数中仍有:乘积是1的两个数互为倒数.如: -的倒数是-2, -2的倒数是-同学们说说下列各数的倒数:1, -1 , 5, -5 ,0有倒数吗?
倒数是它本身的数有 个,分别是 .
数a(a≠0)的倒数是 .0没有倒数.21和-1预习了吗?评价一下!(- 1)×5 = (-3)×(-8) =
(-9)×0 = (+6)×0 = -52400你可以计算了吗?1.计算:(口答) (-3)×9 (2) 6×(-9) (3) (-4)×6
(4) (-6)×(-1) (5) (-6)×0 (6) ×(- )
2.用正负数表示气温的变化量,上升为正,下降为负,登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?解: (-6)×3 = - 18℃
答:气温下降18℃.=-27=-54=-24=6=03.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?解: (-5)×60 = - 300(元)
答:销售额下降了300元.4.计算下列各题:
(1) (-8)×(-7) (2) 2.9×(-0.4)
(3) 100×(-0.001) (4) ×开拓视野:一、选择题:
1、一个有理数与它的相反数的积是( )
A、一定小于0 B、一定大于0
C、一定不小于0 D、一定不大于0
2、有两个有理数a、b, ab>0,a + b<0.则( )
A、a>0, b>0 B、a<0, b<0
C、a>0, b<0 D、a<0, b>0
3、如果ab=0,那么一定有( )
A、a=b=0 B、a=0
C、a,b至少有一个为0 D、 a,b最多有一个为0
DBC二、从七张标有5、3、1、0、-2、-4、-6的卡片中取出3张卡片,使这3张卡片上的数字乘积是最大,应抽哪3张?使积最小呢?解:积最大的3张是:5、-4、-6
5×(-4)×(-6) = 120积最小的3张是:5、3、-6
5×3×(-6) = -90小结:1.两数相乘,同号得正,异号得负,并把 绝对值相乘。
任何一个数同0相乘,都得0。2.有理数中仍有:乘积是1的两个数互为倒数. 0没有倒数。3.数a(a≠0)的倒数是作业:1、复习本节内容第34页至37页。
2、课外作业:课本第47页
第1题(2)、(4)、(6)
第2题全部
第3题(2)、(4)、(6)
3、预习第37、38页。谢谢各位老师的指导
再 见
