18.2.2菱形的性质
图片预览





文档简介
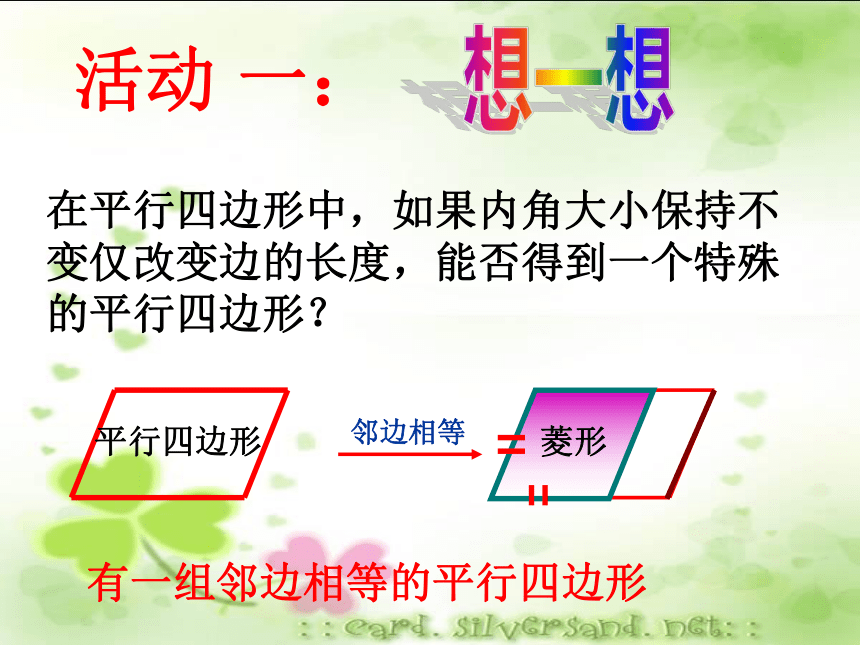
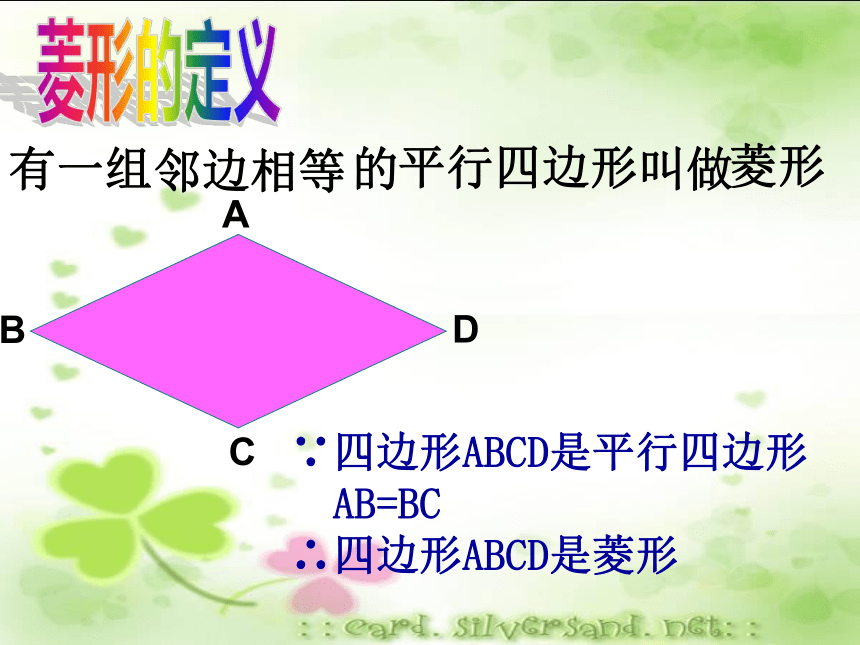
课件25张PPT。18.2特殊的平行四边形18.2.2菱形的性质想一想在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形? 平行四边形 菱形活动 一:菱形的定义有一组 的 叫做邻边相等 平行四边形 ADCB∵四边形ABCD是平行四边形 AB=BC
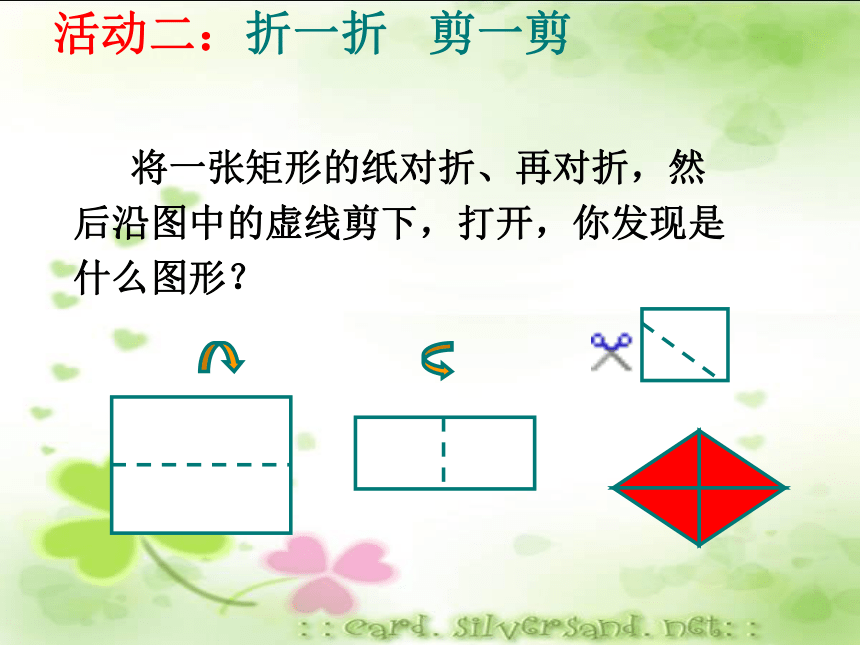
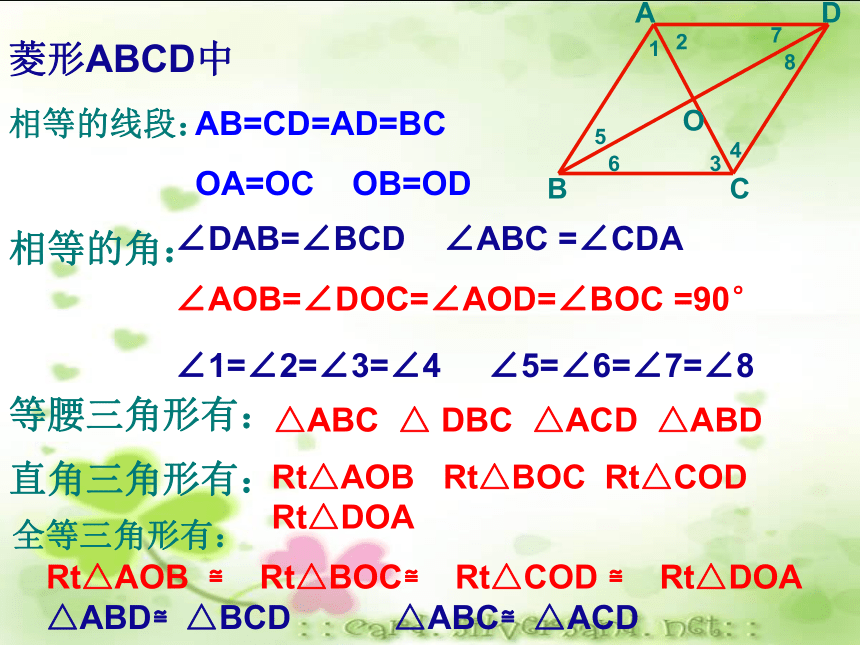
∴四边形ABCD是菱形菱形 感受生活你能举出生活中你看到的菱形吗? 将一张矩形的纸对折、再对折,然后沿图中的虚线剪下,打开,你发现是什么图形?活动二:折一折 剪一剪画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:1、菱形是轴对称图形吗?2、菱形有几条对称轴?3、对称轴之间有什么关系?4、你能看出图中哪些线段和角相等?相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:菱形ABCD中AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678探究菱形的性质菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
菱形的四条边相等菱形是轴对称图形,也是中心对称图形
已知:如图四边形ABCD是菱形求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。证明(1)∵四边形ABCD是菱形∴DA=DC(菱形的定义)∵DA=BC,AB=DC∴AB=BC=DC=DA(2)在△DAC中 ∵AD=CD,AO=CO∴DB⊥AC,
DB平分∠ADC(三线合一)同理: DB平分∠ABC;
AC平分∠DAB和∠DCB(1)AB=BC=CD=DA (2)AC⊥BD AC平分∠DAB和∠DCB BD平分∠ADC和∠ABC求证:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;菱形的性质1、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积。
分析:活动三:做一做菱形的面积公式1、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.1m2 )生活中的数学生活中的数学练一练3cm600C练一练4.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。5.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。2∵四边形ABCD是菱形, ∴AD=AB解:∴AD=AB=BD∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)∴ ∠DAB= 60 °, ∴ ∠ABC=120 °(2)∵AE=2, ∴ AB=4 ∴ BD=AB=4∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得 2AO=∴ AC=4(3)在Rt△DAE中,由勾股定理得 DE==2∴ S菱形ABCD=4×2=8(1)6.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75°B.60°C.45°D.30°B有关菱形问题可转化为直角三角形或等腰三角形的问题来解决7.如图,在边长为6的菱形ABCD中, ∠ DAB=60 o ,E是AB的中点,F是AC上的动点,求EF+BF的最小值 对自己说我有哪些收获? 对老师说你还有哪些困惑? 对同学有哪些温馨提示?畅所欲言小结:知识再现1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线、对称性”学而时习之,不亦说乎?教材:练习题
练习册:相应课时一起放飞理想的翅膀
在知识的天空中自由翱翔
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678探究菱形的性质菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
菱形的四条边相等菱形是轴对称图形,也是中心对称图形
已知:如图四边形ABCD是菱形求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。证明(1)∵四边形ABCD是菱形∴DA=DC(菱形的定义)∵DA=BC,AB=DC∴AB=BC=DC=DA(2)在△DAC中 ∵AD=CD,AO=CO∴DB⊥AC,
DB平分∠ADC(三线合一)同理: DB平分∠ABC;
AC平分∠DAB和∠DCB(1)AB=BC=CD=DA (2)AC⊥BD AC平分∠DAB和∠DCB BD平分∠ADC和∠ABC求证:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;菱形的性质1、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积。
分析:活动三:做一做菱形的面积公式1、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.1m2 )生活中的数学生活中的数学练一练3cm600C练一练4.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。5.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。2∵四边形ABCD是菱形, ∴AD=AB解:∴AD=AB=BD∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)∴ ∠DAB= 60 °, ∴ ∠ABC=120 °(2)∵AE=2, ∴ AB=4 ∴ BD=AB=4∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得 2AO=∴ AC=4(3)在Rt△DAE中,由勾股定理得 DE==2∴ S菱形ABCD=4×2=8(1)6.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75°B.60°C.45°D.30°B有关菱形问题可转化为直角三角形或等腰三角形的问题来解决7.如图,在边长为6的菱形ABCD中, ∠ DAB=60 o ,E是AB的中点,F是AC上的动点,求EF+BF的最小值 对自己说我有哪些收获? 对老师说你还有哪些困惑? 对同学有哪些温馨提示?畅所欲言小结:知识再现1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线、对称性”学而时习之,不亦说乎?教材:练习题
练习册:相应课时一起放飞理想的翅膀
在知识的天空中自由翱翔
