15.3 第2课时 等腰三角形的性质的应用 课件(共21张PPT) 沪科版八年级上册数学
文档属性
| 名称 | 15.3 第2课时 等腰三角形的性质的应用 课件(共21张PPT) 沪科版八年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 15:11:04 | ||
图片预览







文档简介
(共21张PPT)
第15章 轴对称图形与等腰三角形
15.3 等腰三角形
第2课时 等腰三角形的性质的应用
1.能用等腰三角形的性质进行几何图形中的计算.
2.能用等腰三角形的性质解决几何问题中的证明.
3.经历用等腰三角形的性质证明“HL”定理的过程.
◎重点:用等腰三角形的性质进行计算和证明.
◎难点:综合解决几何问题.
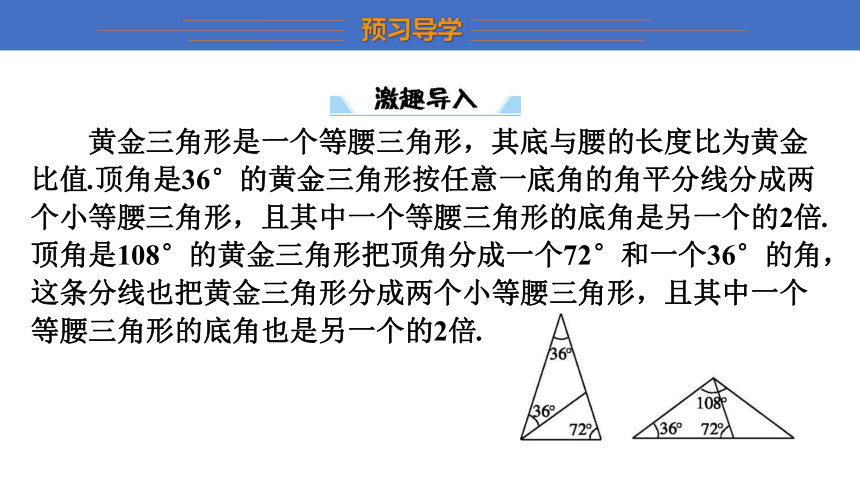
黄金三角形是一个等腰三角形,其底与腰的长度比为黄金比值.顶角是36°的黄金三角形按任意一底角的角平分线分成两个小等腰三角形,且其中一个等腰三角形的底角是另一个的2倍.顶角是108°的黄金三角形把顶角分成一个72°和一个36°的角,这条分线也把黄金三角形分成两个小等腰三角形,且其中一个等腰三角形的底角也是另一个的2倍.
等腰三角形的性质应用
阅读教材本课时所有内容,解决下列问题.
思考:“例2”图中有几个等腰三角形?分别是哪几个?
3个,分别是△ABC,△BDC,△ADB.
1.如图,在Rt△ABC中,∠ACB=90°,以B为圆心,BC的长为半径画弧,交AB于点D,连接CD,∠ACD=20°,则∠A的度数是( A )
A.50°
B.40°
C.30°
D.20°
A
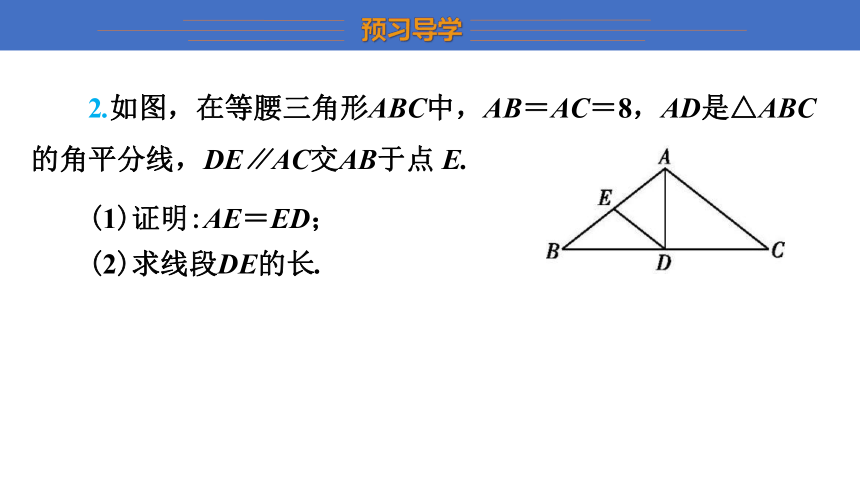
2.如图,在等腰三角形ABC中,AB=AC=8,AD是△ABC的角平分线,DE∥AC交AB于点 E.
(1)证明:AE=ED;
(2)求线段DE的长.
解:(1)∵AD平分∠BAC,
∴∠EAD=∠CAD.
∵DE∥AC,
∴∠ADE=∠CAD,
∴∠EAD=∠ADE,
∴AE=DE.
(2)∵DE∥AC,
∴∠EDB=∠C.
∵AB=AC,
∴∠B=∠C,
∴∠EDB=∠B,
∴BE=DE,
∴DE=BE=AE=AB=×8=4.
利用等腰三角形的性质进行计算
1. 如图,直线l1∥l2,点A在直线l1上,以A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( C )
A.36° B.54° C.72° D.73°
C
2. 如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,求∠OEC的度数.
解:如图,连接OB、OC,
∵∠BAC=54°,AO为∠BAC的平分线,
∴∠BAO=∠BAC=×54°=27°.
又∵AB=AC,∴∠ABC=(180°-∠BAC)
=(180°-54°)=63°,
∵DO是AB的垂直平分线,
∴OA=OB,∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC-∠ABO=63°-27°=36°.
∵DO是AB的垂直平分线,AO为∠BAC的平分线,
∴点O在BC的垂直平分线上(等腰三角形“三线合一”),
∴OB=OC,∴∠OCB=∠OBC=36°.
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°.
3. 如图,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=BE,求∠A的度数.
解:设∠A=x,∵AD=DE=BE,
∴∠A=∠DEA=x,
∴∠EDB=∠DBA=∠DEA=x.
∵BD=BC,∴∠C=∠BDC=∠A+∠DBA=x.
∵AB=AC,∴∠C=∠ABC=x.
∵∠C+∠ABC+∠A=180°,∴x+x+x=180°,
解得x=45°.
【方法归纳交流】解本类题的关键是先设未知数,再用等腰三角形的性质及三角形的内角和构建方程求解.
利用等腰三角形的性质进行证明
4. 如图,在△ABC中,AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C.
证明:如图,延长AB到点F,使AF=AC,连接DF.
∵AC=AB+BD,AF=AC,∴BD=BF,∴∠F=∠BDF.
∵∠ABC=∠F+∠BDF,
∴∠ABC=2∠F.
在△ADF和△ADC中,
∴△ADF≌△ADC(SAS),
∴∠C=∠F,∴∠ABC=2∠C.
【方法归纳交流】构造等腰三角形——截长补短法添加辅助线是应用等腰三角形的性质解决问题的常见题型.“三线合一”中的“线”也是等腰三角形中常添加的辅助线.
1.如图,CD是△ABC的中线,且CD=AB,你知道∠ACB的度数吗?由此你能得到一个什么结论?
解:∠ACB的度数是90°,理由如下:
∵CD是△ABC的中线,且CD=AB,
∴∠A=∠ACD,∠B=∠BCD.
∵∠A+∠ACD+∠B+∠BCD=180°,
∴∠ACB=90°.
结论:一边上的中线等于这边一半的三角形是直角三角形.
2. 如图,在等边三角形ABC中,点D在AB上,点E在BC上,AD=BE,AE、CD相交于点P.求证:∠CPE=60°.
证明:∵△ABC是等边三角形,
∴∠B=∠BAC=60°,AB=CA.
又∵BE=AD,∴△ABE≌△CAD,
∴∠BAE=∠ACD,
又∵∠CPE是△APC的一个外角,
∴∠CPE=∠PAC+∠ACD=∠EAC+∠BAE=∠BAC.
∵∠BAC=60°,∴∠CPE=60°.
第15章 轴对称图形与等腰三角形
15.3 等腰三角形
第2课时 等腰三角形的性质的应用
1.能用等腰三角形的性质进行几何图形中的计算.
2.能用等腰三角形的性质解决几何问题中的证明.
3.经历用等腰三角形的性质证明“HL”定理的过程.
◎重点:用等腰三角形的性质进行计算和证明.
◎难点:综合解决几何问题.
黄金三角形是一个等腰三角形,其底与腰的长度比为黄金比值.顶角是36°的黄金三角形按任意一底角的角平分线分成两个小等腰三角形,且其中一个等腰三角形的底角是另一个的2倍.顶角是108°的黄金三角形把顶角分成一个72°和一个36°的角,这条分线也把黄金三角形分成两个小等腰三角形,且其中一个等腰三角形的底角也是另一个的2倍.
等腰三角形的性质应用
阅读教材本课时所有内容,解决下列问题.
思考:“例2”图中有几个等腰三角形?分别是哪几个?
3个,分别是△ABC,△BDC,△ADB.
1.如图,在Rt△ABC中,∠ACB=90°,以B为圆心,BC的长为半径画弧,交AB于点D,连接CD,∠ACD=20°,则∠A的度数是( A )
A.50°
B.40°
C.30°
D.20°
A
2.如图,在等腰三角形ABC中,AB=AC=8,AD是△ABC的角平分线,DE∥AC交AB于点 E.
(1)证明:AE=ED;
(2)求线段DE的长.
解:(1)∵AD平分∠BAC,
∴∠EAD=∠CAD.
∵DE∥AC,
∴∠ADE=∠CAD,
∴∠EAD=∠ADE,
∴AE=DE.
(2)∵DE∥AC,
∴∠EDB=∠C.
∵AB=AC,
∴∠B=∠C,
∴∠EDB=∠B,
∴BE=DE,
∴DE=BE=AE=AB=×8=4.
利用等腰三角形的性质进行计算
1. 如图,直线l1∥l2,点A在直线l1上,以A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( C )
A.36° B.54° C.72° D.73°
C
2. 如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,求∠OEC的度数.
解:如图,连接OB、OC,
∵∠BAC=54°,AO为∠BAC的平分线,
∴∠BAO=∠BAC=×54°=27°.
又∵AB=AC,∴∠ABC=(180°-∠BAC)
=(180°-54°)=63°,
∵DO是AB的垂直平分线,
∴OA=OB,∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC-∠ABO=63°-27°=36°.
∵DO是AB的垂直平分线,AO为∠BAC的平分线,
∴点O在BC的垂直平分线上(等腰三角形“三线合一”),
∴OB=OC,∴∠OCB=∠OBC=36°.
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°.
3. 如图,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=BE,求∠A的度数.
解:设∠A=x,∵AD=DE=BE,
∴∠A=∠DEA=x,
∴∠EDB=∠DBA=∠DEA=x.
∵BD=BC,∴∠C=∠BDC=∠A+∠DBA=x.
∵AB=AC,∴∠C=∠ABC=x.
∵∠C+∠ABC+∠A=180°,∴x+x+x=180°,
解得x=45°.
【方法归纳交流】解本类题的关键是先设未知数,再用等腰三角形的性质及三角形的内角和构建方程求解.
利用等腰三角形的性质进行证明
4. 如图,在△ABC中,AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C.
证明:如图,延长AB到点F,使AF=AC,连接DF.
∵AC=AB+BD,AF=AC,∴BD=BF,∴∠F=∠BDF.
∵∠ABC=∠F+∠BDF,
∴∠ABC=2∠F.
在△ADF和△ADC中,
∴△ADF≌△ADC(SAS),
∴∠C=∠F,∴∠ABC=2∠C.
【方法归纳交流】构造等腰三角形——截长补短法添加辅助线是应用等腰三角形的性质解决问题的常见题型.“三线合一”中的“线”也是等腰三角形中常添加的辅助线.
1.如图,CD是△ABC的中线,且CD=AB,你知道∠ACB的度数吗?由此你能得到一个什么结论?
解:∠ACB的度数是90°,理由如下:
∵CD是△ABC的中线,且CD=AB,
∴∠A=∠ACD,∠B=∠BCD.
∵∠A+∠ACD+∠B+∠BCD=180°,
∴∠ACB=90°.
结论:一边上的中线等于这边一半的三角形是直角三角形.
2. 如图,在等边三角形ABC中,点D在AB上,点E在BC上,AD=BE,AE、CD相交于点P.求证:∠CPE=60°.
证明:∵△ABC是等边三角形,
∴∠B=∠BAC=60°,AB=CA.
又∵BE=AD,∴△ABE≌△CAD,
∴∠BAE=∠ACD,
又∵∠CPE是△APC的一个外角,
∴∠CPE=∠PAC+∠ACD=∠EAC+∠BAE=∠BAC.
∵∠BAC=60°,∴∠CPE=60°.
