15.4 角的平分线 第1课时 尺规作图 课件(共15张PPT) 沪科版八年级上册数学
文档属性
| 名称 | 15.4 角的平分线 第1课时 尺规作图 课件(共15张PPT) 沪科版八年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 737.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第15章 轴对称图形与等腰三角形
15.4 角的平分线
第1课时 尺规作图
1.知道角是轴对称图形,掌握角平分线的尺规作法并会证明它的正确性.
2.掌握过一点作已知直线垂线的尺规作法.
3.增强动手画图的能力,进一步理解尺规作图的准确性.
◎重点:角平分线及垂线的尺规作法.
◎难点:体会尺规作图的意义.
把一块纸片对折,使一个角的两边叠合在一起,把纸片展开后,用量角器量一量由折痕为边的两个角的度数.
角平分线的作法
阅读教材本课时相关内容,回答下列问题.
角是轴对称图形吗?如果是,指出其对称轴.
是轴对称图形,其对称轴是角平分线所在的直线.
过一点作已知直线的垂线
揭示概念:过一点作已知直线的垂线其实质就是作平角的 角平分线 或作线段的 垂直平分线 .
角平分线
垂直平分线
1.下列尺规作图的语句正确的是( C )
A.作∠AOB的平分线AC
B.以O为圆心作弧
C.以A为圆心,线段a的长为半径作弧
D.作直线AB的垂直平分线CD
C
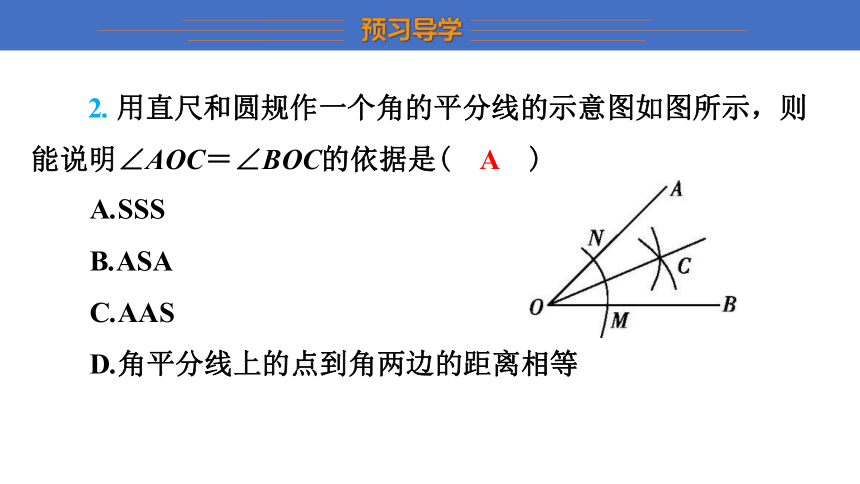
2. 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( A )
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
过一点作已知线的垂线
1.(方法指导:延长线段AB,就是过点P作直线AB的垂线)如图,已知线段AB和一点P,用尺规过点P作AB的垂线PO(保留作图痕迹,不写作法).
解:如图.
作等腰三角形
2. 已知底边及底边上的高作等腰三角形.
已知:线段a、b .
求作:等腰三角形,使底长为a,底边上的高为b.
解:作法:1.作射线AM;
2.在射线AM上截取线段AB,使AB=a;
3.作线段AB的垂直平分线DE,交AB于点D;
4.在射线DE上截取线段DC,使DC=b;
5.连接AC、BC.
△ABC就是所求作的等腰三角形.
【方法归纳交流】在利用几种基本作图作较复杂的图形时,首先可以画出一个草图进行分析,需要使用哪些基本作图,作图的先后顺序如何,用到的基本作图可以用一句话叙述.
作角平分线和垂直平分线
3. 已知△ABC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法),并根据要求填空.
(1)作∠ABC的平分线BD交AC于点D;
(2)作线段BD的垂直平分线交AB于点E,交BC于点F,线段EF与线段BD的关系为 .
解:(1)、(2)题作图如下:由作图可知线段EF与线段BD的关系为互相垂直平分.
已知三角形中的一个角,此角的平分线长,以及这个角的一边长,求作三角形.
已知:∠α,以及线段b、c(b<c).求作:△ABC,使得∠BAC=∠α,AB=c,∠BAC的平分线AD=b.
解:作法:(1)作∠MAN=∠α.
(2)作∠MAN的平分线AE.
(3)在AM上截取AB=c,在AE上截取AD=b.
(4)连接BD,并延长交AN于点C.
△ABC就是所求作的三角形.(如图)
第15章 轴对称图形与等腰三角形
15.4 角的平分线
第1课时 尺规作图
1.知道角是轴对称图形,掌握角平分线的尺规作法并会证明它的正确性.
2.掌握过一点作已知直线垂线的尺规作法.
3.增强动手画图的能力,进一步理解尺规作图的准确性.
◎重点:角平分线及垂线的尺规作法.
◎难点:体会尺规作图的意义.
把一块纸片对折,使一个角的两边叠合在一起,把纸片展开后,用量角器量一量由折痕为边的两个角的度数.
角平分线的作法
阅读教材本课时相关内容,回答下列问题.
角是轴对称图形吗?如果是,指出其对称轴.
是轴对称图形,其对称轴是角平分线所在的直线.
过一点作已知直线的垂线
揭示概念:过一点作已知直线的垂线其实质就是作平角的 角平分线 或作线段的 垂直平分线 .
角平分线
垂直平分线
1.下列尺规作图的语句正确的是( C )
A.作∠AOB的平分线AC
B.以O为圆心作弧
C.以A为圆心,线段a的长为半径作弧
D.作直线AB的垂直平分线CD
C
2. 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( A )
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
过一点作已知线的垂线
1.(方法指导:延长线段AB,就是过点P作直线AB的垂线)如图,已知线段AB和一点P,用尺规过点P作AB的垂线PO(保留作图痕迹,不写作法).
解:如图.
作等腰三角形
2. 已知底边及底边上的高作等腰三角形.
已知:线段a、b .
求作:等腰三角形,使底长为a,底边上的高为b.
解:作法:1.作射线AM;
2.在射线AM上截取线段AB,使AB=a;
3.作线段AB的垂直平分线DE,交AB于点D;
4.在射线DE上截取线段DC,使DC=b;
5.连接AC、BC.
△ABC就是所求作的等腰三角形.
【方法归纳交流】在利用几种基本作图作较复杂的图形时,首先可以画出一个草图进行分析,需要使用哪些基本作图,作图的先后顺序如何,用到的基本作图可以用一句话叙述.
作角平分线和垂直平分线
3. 已知△ABC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法),并根据要求填空.
(1)作∠ABC的平分线BD交AC于点D;
(2)作线段BD的垂直平分线交AB于点E,交BC于点F,线段EF与线段BD的关系为 .
解:(1)、(2)题作图如下:由作图可知线段EF与线段BD的关系为互相垂直平分.
已知三角形中的一个角,此角的平分线长,以及这个角的一边长,求作三角形.
已知:∠α,以及线段b、c(b<c).求作:△ABC,使得∠BAC=∠α,AB=c,∠BAC的平分线AD=b.
解:作法:(1)作∠MAN=∠α.
(2)作∠MAN的平分线AE.
(3)在AM上截取AB=c,在AE上截取AD=b.
(4)连接BD,并延长交AN于点C.
△ABC就是所求作的三角形.(如图)
