21.4 二次函数的应用第1课时 建立二次函数模型解决实际问题课件(共34张PPT) 沪科版九年级上册数学
文档属性
| 名称 | 21.4 二次函数的应用第1课时 建立二次函数模型解决实际问题课件(共34张PPT) 沪科版九年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 15:16:00 | ||
图片预览











文档简介
(共34张PPT)
第21章 二次函数与反比例函数
21.4 二次函数的应用
第1课时 建立二次函数模型解决实际问题
1.建立二次函数模型,解决几何图形面积的最值问题.
2.会用二次函数解决拱桥、隧道等抛物线形物体的相关问题.
3.体会数学建模的思想,感受数学的应用价值.
◎重点:建立二次函数模型.
◎难点:根据实际问题,建立二次函数模型.
二次函数的有关知识在经济生活中的应用更为广阔,我们来看这样一个生活中常见的问题:某广告公司设计一幅周长为8米的矩形广告牌,广告设计费为每平方米1000元,设矩形一边长为x米,面积为S平方米.请你设计一个方案,使获得的设计费最多.类似的问题,我们都可以通过建立二次函数的数学模型来解决.
图形面积问题
阅读课本本课时“例1”,回答下列问题.
1.设水面的一边长为x,则另一边长为 20-x ,面积可表示为S= -x2+20x .
2.说一说:开口向下的二次函数,有最 大 值,即顶点坐标的 纵 坐标.
20-x
-x2+20x
大
纵
归纳总结 解二次函数最值问题的一般步骤:
(1)设未知数,列出二次函数的表达式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值.
抛物线形物体的相关问题
阅读课本本课时“例2”,回答下列问题.
(1)“例2”中,以桥面所在的直线为x轴有什么好处?以抛物线的对称轴为y轴建立平面直角坐标系有什么好处?
这样建立x轴,则某点处的纵坐标就是该点悬索的高度;以对称轴为y轴,则二次函数表达式较简单,为y=ax2+k的形式.
(2)建立坐标系的过程,运用了什么数学思想?
运用了数学建模的思想,将一个实际问题转化为可以用二次函数解决的问题.
归纳总结 用函数的思想方法解决抛物线形拱桥问题:①先建立恰当的 平面直角坐标系 ;②根据已知条件,对应二次函数上的点,求出函数 表达式 ;③根据已知条件找到抛物线上某些特殊位置的 横 坐标,利用二次函数知识解决问题.
平面直角坐标系
表达式
横
1.用总长为60 m的篱笆围成矩形场地,设矩形的长为x m,则该矩形的宽为 (30-x) m.若用S表示该矩形场地的面积,则S关于x的函数表达式为 S=x(30-x)(0<x<30) ,将该函数表达式配方成顶点式,得 S=-(x-15)2+225 .因为抛物线S的开口向下,故当x= 15 时,函数S的最大值为 225 .
(30-x)
S=x(30-x)(0<x<30)
S=-(x-15)2+225
15
225
2.一座石拱桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数关系式为y=-x2,当水面离桥拱顶的高度OC是4 m时,水面的宽度AB为 16 m .
16 m
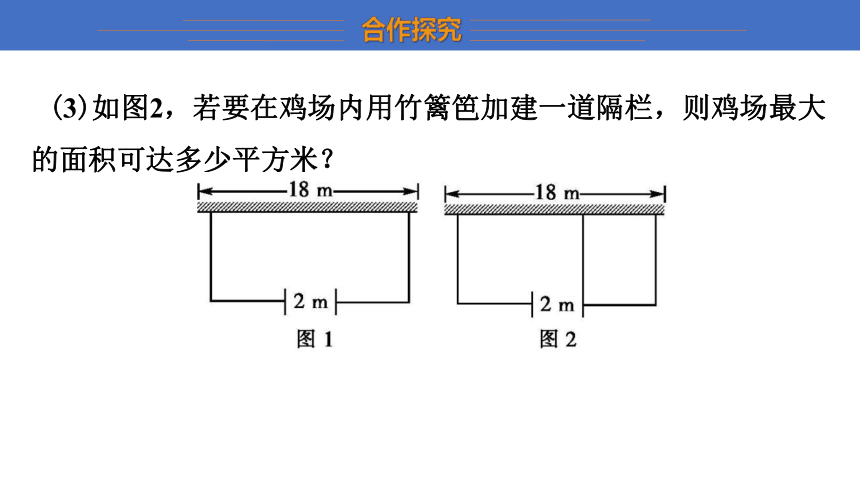
1.如图1,若要建一个长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
问:(1)若鸡场的面积为150平方米,鸡场的长和宽各为多少米?
(2)鸡场面积可能达到200平方米吗?
(3)如图2,若要在鸡场内用竹篱笆加建一道隔栏,则鸡场最大的面积可达多少平方米?
解:(1)设宽为x米,则x(33-2x+2)=150,解得x1=10,x2=(不合题意,舍去),
∴长为15米,宽为10米.
(2)设面积为W平方米,则W=x(33-2x+2).变形为W=-22+,
∴鸡场面积的最大值为153<200,即不可能达到200平方米.
(3)设此时面积为Q平方米,宽为x米.则Q=x(33-3x+2),变形得Q=-32+,∴此时鸡场面积的最大值为.
2.如图,有一个抛物线形的拱形立交桥,这个桥拱的最大高度为16 m,跨度为40 m,现把它放在如图所示的直角坐标系里,若要在离跨度中心点M的5 m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长?
解:由题意,知抛物线的顶点坐标为(20,16),点B(40,0),
∴可设抛物线的表达式为y=a(x-20)2+16.
∵点B(40,0)在抛物线上,∴a(40-20)2+16=0,
∴a=-,∴y=-(x-20)2+16.
∵竖立柱脚的点为(15,0)或(25,0),
∴当x=15时,y=-(15-20)2+16=15(m);
当x=25时,y=-(25-20)2+16=15(m),
∴铁柱应取15 m.
方法归纳交流 解决这类题的基本思路:(1)理解题意;(2)找出问题中的两个变量,用待. 定. 系. 数. 法. 或根. 据. 实. 际. 意 . 义. 求出 函数表达式 ;(3)结合函数 图象 或 性质 求解;(4)注意自变量的 取值范围 ,检验结果的合理性.
函数表达式
图象
性质
取值范围
1.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80 m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x m,矩形区域ABCD的面积为y m2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围.
(2)x为何值时,y有最大值?最大值是多少?
解:(1)方法一:设AE=a,由题意得AE·AD=2BE·BC,AD=BC,∴BE=a,AB=a.由题意得2x+3a+2×a=80,∴a=20-x,y=AB·BC=a·x=x,即y=-x2+30x,其中0<x<40.
方法二:根据题意得CF·x=,CF=,DF·x=,DF=,∴2x+2×+3×=80,整理得y=-x2+30x,其中0<x<40.
(2)y=-x2+30x=-(x-20)2+300,由于-<0,抛物线开口向下,又∵0<x<40,∴当x=20时,y取最大值,最大值是300.
2.某家禽养殖场用总长为110 m的围栏靠墙(墙长为22 m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF的面积都等于矩形BFHG面积的一半,设AD的长为x m,矩形区域ABCD的面积为y m2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围.
(2)当x为何值时,y有最大值?最大值是多少?
解:(1)∵矩形AEHG与矩形CDEF的面积都等于矩形BFHG面积的一半,
∴矩形AEFB面积是矩形CDEF面积的3倍,∴AE=3DE.∵AD=x,∴GH=x.
∵围栏总长为110 m,∴2x+x+2CD=110,
∴CD=55-x,∴y=x=-x2+55x,
∴自变量x的取值范围为24≤x<40.
(2)∵y=-x2+55x=-(x2-40x)=-(x-20)2+550,
∵自变量x的取值范围为24≤x<40,且二次项系数为-<0,
∴当x=24时,y有最大值,最大值为528平方米.
3.某河上一座古拱桥的截面图如图1所示,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是1 m,拱桥的跨度为10 m.桥洞与水面的最大距离是5 m.桥洞两侧壁上各有一盏距离水面4 m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图2.求:
(1)抛物线的表达式;
(2)两盏景观灯P1、P2之间的水平距离.
解:(1)抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1),
设抛物线的表达式是y=a(x-5)2+5.
把(0,1)代入y=a(x-5)2+5,得a=-,
∴y=-(x-5)2+5(0≤x≤10).
(2)由已知得两景观灯的纵坐标都是4,
∴4=-(x-5)2+5,∴(x-5)2=1,
∴x1=,x2=,∴两景观灯间的距离为-=5米.
4.如图,这是一座抛物线形拱桥,在正常水位时,水面AB宽20 m,水位上升3 m就达到了警戒线CD,这时水面宽度为10 m.
(1)建立如图所示的直角坐标系,求抛物线的函数表达式.
(2)若洪水到来时,水位以0.2 m/h的速度上升,从警戒线开始,再持续多少小时能到桥顶?
解:(1)设抛物线的函数表达式为y=ax2,A点的坐标为(-10,n),则C点的坐标为(-5,n+3),
∴解得∴抛物线的表达式为y=-x2.
(2)由(1)可知,点C的坐标为(-5,-1),即再持续=5 h水位将升到桥顶.
1.如图,一边靠墙(墙有足够长),三边用12 m长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是 ( C )
A.16 m2 B.12 m2
C.18 m2 D.以上都不对
C
2.如图,这是抛物线型拱桥,当拱顶离水面2 m时,水面宽4 m,若水面下降2 m,则水面宽度增加 4-4 m.
4-4
3.如图,一座悬索桥的桥面OA与主悬钢索MN之间用垂直钢索连接,主悬钢索是抛物线形状,两端到桥面的距离OM与AN相等,小强骑自行车从桥的一端O沿直线匀速穿过桥面到达另一端A,当他行驶18秒时和28秒时所在地方的主悬钢索的高度相同,那么他通过整个桥面OA共需 46 秒.
46
第21章 二次函数与反比例函数
21.4 二次函数的应用
第1课时 建立二次函数模型解决实际问题
1.建立二次函数模型,解决几何图形面积的最值问题.
2.会用二次函数解决拱桥、隧道等抛物线形物体的相关问题.
3.体会数学建模的思想,感受数学的应用价值.
◎重点:建立二次函数模型.
◎难点:根据实际问题,建立二次函数模型.
二次函数的有关知识在经济生活中的应用更为广阔,我们来看这样一个生活中常见的问题:某广告公司设计一幅周长为8米的矩形广告牌,广告设计费为每平方米1000元,设矩形一边长为x米,面积为S平方米.请你设计一个方案,使获得的设计费最多.类似的问题,我们都可以通过建立二次函数的数学模型来解决.
图形面积问题
阅读课本本课时“例1”,回答下列问题.
1.设水面的一边长为x,则另一边长为 20-x ,面积可表示为S= -x2+20x .
2.说一说:开口向下的二次函数,有最 大 值,即顶点坐标的 纵 坐标.
20-x
-x2+20x
大
纵
归纳总结 解二次函数最值问题的一般步骤:
(1)设未知数,列出二次函数的表达式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值.
抛物线形物体的相关问题
阅读课本本课时“例2”,回答下列问题.
(1)“例2”中,以桥面所在的直线为x轴有什么好处?以抛物线的对称轴为y轴建立平面直角坐标系有什么好处?
这样建立x轴,则某点处的纵坐标就是该点悬索的高度;以对称轴为y轴,则二次函数表达式较简单,为y=ax2+k的形式.
(2)建立坐标系的过程,运用了什么数学思想?
运用了数学建模的思想,将一个实际问题转化为可以用二次函数解决的问题.
归纳总结 用函数的思想方法解决抛物线形拱桥问题:①先建立恰当的 平面直角坐标系 ;②根据已知条件,对应二次函数上的点,求出函数 表达式 ;③根据已知条件找到抛物线上某些特殊位置的 横 坐标,利用二次函数知识解决问题.
平面直角坐标系
表达式
横
1.用总长为60 m的篱笆围成矩形场地,设矩形的长为x m,则该矩形的宽为 (30-x) m.若用S表示该矩形场地的面积,则S关于x的函数表达式为 S=x(30-x)(0<x<30) ,将该函数表达式配方成顶点式,得 S=-(x-15)2+225 .因为抛物线S的开口向下,故当x= 15 时,函数S的最大值为 225 .
(30-x)
S=x(30-x)(0<x<30)
S=-(x-15)2+225
15
225
2.一座石拱桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数关系式为y=-x2,当水面离桥拱顶的高度OC是4 m时,水面的宽度AB为 16 m .
16 m
1.如图1,若要建一个长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
问:(1)若鸡场的面积为150平方米,鸡场的长和宽各为多少米?
(2)鸡场面积可能达到200平方米吗?
(3)如图2,若要在鸡场内用竹篱笆加建一道隔栏,则鸡场最大的面积可达多少平方米?
解:(1)设宽为x米,则x(33-2x+2)=150,解得x1=10,x2=(不合题意,舍去),
∴长为15米,宽为10米.
(2)设面积为W平方米,则W=x(33-2x+2).变形为W=-22+,
∴鸡场面积的最大值为153<200,即不可能达到200平方米.
(3)设此时面积为Q平方米,宽为x米.则Q=x(33-3x+2),变形得Q=-32+,∴此时鸡场面积的最大值为.
2.如图,有一个抛物线形的拱形立交桥,这个桥拱的最大高度为16 m,跨度为40 m,现把它放在如图所示的直角坐标系里,若要在离跨度中心点M的5 m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长?
解:由题意,知抛物线的顶点坐标为(20,16),点B(40,0),
∴可设抛物线的表达式为y=a(x-20)2+16.
∵点B(40,0)在抛物线上,∴a(40-20)2+16=0,
∴a=-,∴y=-(x-20)2+16.
∵竖立柱脚的点为(15,0)或(25,0),
∴当x=15时,y=-(15-20)2+16=15(m);
当x=25时,y=-(25-20)2+16=15(m),
∴铁柱应取15 m.
方法归纳交流 解决这类题的基本思路:(1)理解题意;(2)找出问题中的两个变量,用待. 定. 系. 数. 法. 或根. 据. 实. 际. 意 . 义. 求出 函数表达式 ;(3)结合函数 图象 或 性质 求解;(4)注意自变量的 取值范围 ,检验结果的合理性.
函数表达式
图象
性质
取值范围
1.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80 m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x m,矩形区域ABCD的面积为y m2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围.
(2)x为何值时,y有最大值?最大值是多少?
解:(1)方法一:设AE=a,由题意得AE·AD=2BE·BC,AD=BC,∴BE=a,AB=a.由题意得2x+3a+2×a=80,∴a=20-x,y=AB·BC=a·x=x,即y=-x2+30x,其中0<x<40.
方法二:根据题意得CF·x=,CF=,DF·x=,DF=,∴2x+2×+3×=80,整理得y=-x2+30x,其中0<x<40.
(2)y=-x2+30x=-(x-20)2+300,由于-<0,抛物线开口向下,又∵0<x<40,∴当x=20时,y取最大值,最大值是300.
2.某家禽养殖场用总长为110 m的围栏靠墙(墙长为22 m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF的面积都等于矩形BFHG面积的一半,设AD的长为x m,矩形区域ABCD的面积为y m2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围.
(2)当x为何值时,y有最大值?最大值是多少?
解:(1)∵矩形AEHG与矩形CDEF的面积都等于矩形BFHG面积的一半,
∴矩形AEFB面积是矩形CDEF面积的3倍,∴AE=3DE.∵AD=x,∴GH=x.
∵围栏总长为110 m,∴2x+x+2CD=110,
∴CD=55-x,∴y=x=-x2+55x,
∴自变量x的取值范围为24≤x<40.
(2)∵y=-x2+55x=-(x2-40x)=-(x-20)2+550,
∵自变量x的取值范围为24≤x<40,且二次项系数为-<0,
∴当x=24时,y有最大值,最大值为528平方米.
3.某河上一座古拱桥的截面图如图1所示,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是1 m,拱桥的跨度为10 m.桥洞与水面的最大距离是5 m.桥洞两侧壁上各有一盏距离水面4 m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图2.求:
(1)抛物线的表达式;
(2)两盏景观灯P1、P2之间的水平距离.
解:(1)抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1),
设抛物线的表达式是y=a(x-5)2+5.
把(0,1)代入y=a(x-5)2+5,得a=-,
∴y=-(x-5)2+5(0≤x≤10).
(2)由已知得两景观灯的纵坐标都是4,
∴4=-(x-5)2+5,∴(x-5)2=1,
∴x1=,x2=,∴两景观灯间的距离为-=5米.
4.如图,这是一座抛物线形拱桥,在正常水位时,水面AB宽20 m,水位上升3 m就达到了警戒线CD,这时水面宽度为10 m.
(1)建立如图所示的直角坐标系,求抛物线的函数表达式.
(2)若洪水到来时,水位以0.2 m/h的速度上升,从警戒线开始,再持续多少小时能到桥顶?
解:(1)设抛物线的函数表达式为y=ax2,A点的坐标为(-10,n),则C点的坐标为(-5,n+3),
∴解得∴抛物线的表达式为y=-x2.
(2)由(1)可知,点C的坐标为(-5,-1),即再持续=5 h水位将升到桥顶.
1.如图,一边靠墙(墙有足够长),三边用12 m长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是 ( C )
A.16 m2 B.12 m2
C.18 m2 D.以上都不对
C
2.如图,这是抛物线型拱桥,当拱顶离水面2 m时,水面宽4 m,若水面下降2 m,则水面宽度增加 4-4 m.
4-4
3.如图,一座悬索桥的桥面OA与主悬钢索MN之间用垂直钢索连接,主悬钢索是抛物线形状,两端到桥面的距离OM与AN相等,小强骑自行车从桥的一端O沿直线匀速穿过桥面到达另一端A,当他行驶18秒时和28秒时所在地方的主悬钢索的高度相同,那么他通过整个桥面OA共需 46 秒.
46
