22.3 相似三角形的性质课件(共24张PPT) 沪科版九年级上册数学
文档属性
| 名称 | 22.3 相似三角形的性质课件(共24张PPT) 沪科版九年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 15:16:29 | ||
图片预览








文档简介
(共24张PPT)
第22章 相似形
22.3 相似三角形的性质
1.理解两个相似三角形中的对应特殊线段(高、中线、角平分线)的比等于相似比.
2.理解两个相似三角形周长之比等于相似比.
3.理解两个相似三角形面积之比等于相似比的平方.
◎重点:相似三角形的性质.
◎难点:相似三角形性质的应用.
图中是两个相似的西红柿,之前我们知道相似多边形对应边的比是相似比,那么这两只西红柿图片的面积比也等于相似比吗?
相似三角形中的特殊线段
阅读课本本课时“思考”之前的内容,试完成下列问题.
1.在“图22-23”中,作两个相似三角形的高,可以很容易得到两个直角三角形两个内角对应 相等 ,从而得到另外一组相似三角形.
相等
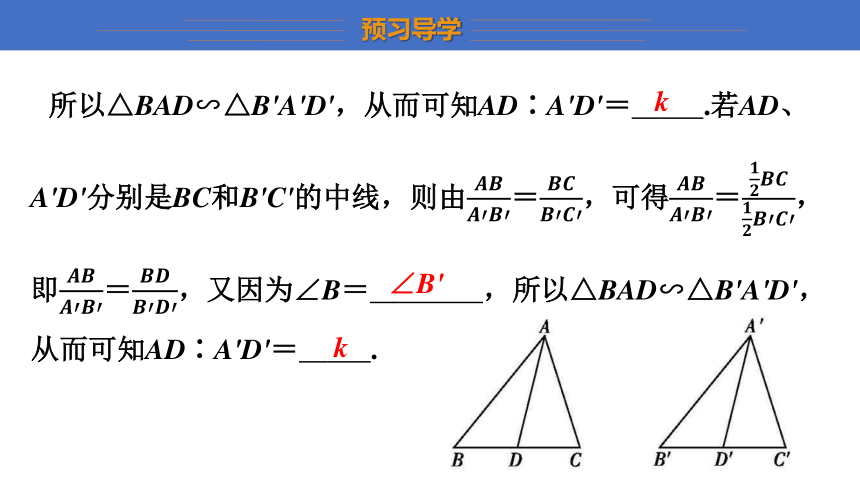
2.如图,△ABC∽△A'B'C',相似比为k,若AD、A'D'分别是∠BAC和∠B'A'C'的平分线,则由∠BAC=∠B'A'C'可得∠BAD= ∠B'A'D' ,又因为∠B= ∠B' ,
∠B'A'D'
∠B'
所以△BAD∽△B'A'D',从而可知AD∶A'D'= k .若AD、A'D'分别是BC和B'C'的中线,则由=,可得=,即=,又因为∠B= ∠B' ,所以△BAD∽△B'A'D',从而可知AD∶A'D'= k .
k
∠B'
k
归纳总结 定理1:相似三角形的对应高的比、对应中线的比和对应角平分线的比都等于 相似比 .
相似比
两个全等的三角形,对应的高、中线、角平分线也相等.两个相似三角形,对应的高、中线、角平分线之比等于相似比.
相似三角形的周长之比与面积之比
阅读课本“思考”至“例1”前的内容,完成下面的问题.
1.如果△ABC∽△A'B'C',且相似比为k,那么=== k ,由等比性质,得= k .
k
k
2.如果△ABC∽△A'B'C',且相似比为k,AD、A'D'是对应高,则由三角形的面积公式及定理1,可得==·= k2 .
归纳总结 定理2:相似三角形周长的比等于 相似比 .
定理3:相似三角形面积的比等于 相似比的平方 .
k2
相似比
相似比的平方
让学生经历以上的证明过程,使其理解定理,形成一种对知识规律的认知,往往效果要比死记硬背好得多.
·导学建议·
1.若△AB C∽△AB'C,且面积比为4∶9,则其对应边上的高的比为 ( C )
A. B. C. D.
2.已知△ABC的三边分别是5,6,7,与它相似△A'B'C'的最短边为10,则△A'B'C'的周长是 36 .
C
36
1.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=5 m,点P到CD的距离是3 m,则P到AB的距离是 ( C )
A. m B. m
C. m D. m
C
2.△ABC与△A1B1C1是相似三角形,且=2,S△ABC=9,则= 36 .
36
3.已知一个三角形的三边长分别是1,2,3,与其相似的三角形的最大边长为3,求较大三角形的周长.
解:∵边长分别是1,2,3的三角形的最大边为3,小于另一
三角形的最大边3,
∴这个三角形的周长等于1+2+3=4+2,
∴它与另一三角形的相似比=3∶3=1∶,
它与另一三角形的周长的比也为1∶,
∴另一三角形的周长=(4+2)×=4+4.
方法归纳交流 利用相似三角形的性质求三角形的周长或面积,一般要知道 相似比 和其中一个三角形的 周长 或 面积 .
相似比
周长
面
积
4.如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求平行四边形ABCD的面积.
解:(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∴∠ABF=∠CEB,
∴△ABF∽△CEB.
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB平行且等于CD,
∴△DEF∽△CEB,△DEF∽△ABF.
∵DE=CD,
∴=2=,=2=.
∵S△DEF=2,
∴S△CEB=18,S△ABF=8.
∵S四边形BCDF=S△BCE-S△DEF=16,
∴S四边形ABCD=S四边形BCDF+S△ABF=16+8=24.
1.如果两个相似三角形的面积之比为9∶4,那么这两个三角形的周长之比为 ( D )
A.81∶16 B.27∶12
C.9∶4 D.3∶2
D
2.如图,李老师用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上,已知直角三角形纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8米,他与“步云阁”的水平距距离CD为104 m,则“步云阁”的高度AB是 ( C )
A.75.5 m B.77.1 m
C.79.8 m D.82.5 m
C
3.已知△ABC∽△DEF,且相似比为2∶3,则下列说法中正确的结论是 ①④ .
①对应中线之比为2∶3;②对应角平分线之比为3∶2;③△ABC与△DEF的周长之比为4∶9;④△ABC与△DEF的面积之比为4∶9.
①④
如图,直角三角形的铁片ABC的两直角边BC、AC的长分别为3 cm和4 cm,分别采用(1)、(2)两种剪法,剪出一块正方形铁片,为使所得的正方形面积最大,问哪一种剪法好?为什么?
解:如图(1),设图中正方形的边长为x cm,则AD=(4-x)cm.
∵DE∥BC,∴=,∴=,
解得x=.
如图(2),设图中正方形的边长为y cm.
∵CH= cm,又△CDE∽△CAB,∴=,
∴=,∴y=.
∵>,∴图(1)中的剪法好.
第22章 相似形
22.3 相似三角形的性质
1.理解两个相似三角形中的对应特殊线段(高、中线、角平分线)的比等于相似比.
2.理解两个相似三角形周长之比等于相似比.
3.理解两个相似三角形面积之比等于相似比的平方.
◎重点:相似三角形的性质.
◎难点:相似三角形性质的应用.
图中是两个相似的西红柿,之前我们知道相似多边形对应边的比是相似比,那么这两只西红柿图片的面积比也等于相似比吗?
相似三角形中的特殊线段
阅读课本本课时“思考”之前的内容,试完成下列问题.
1.在“图22-23”中,作两个相似三角形的高,可以很容易得到两个直角三角形两个内角对应 相等 ,从而得到另外一组相似三角形.
相等
2.如图,△ABC∽△A'B'C',相似比为k,若AD、A'D'分别是∠BAC和∠B'A'C'的平分线,则由∠BAC=∠B'A'C'可得∠BAD= ∠B'A'D' ,又因为∠B= ∠B' ,
∠B'A'D'
∠B'
所以△BAD∽△B'A'D',从而可知AD∶A'D'= k .若AD、A'D'分别是BC和B'C'的中线,则由=,可得=,即=,又因为∠B= ∠B' ,所以△BAD∽△B'A'D',从而可知AD∶A'D'= k .
k
∠B'
k
归纳总结 定理1:相似三角形的对应高的比、对应中线的比和对应角平分线的比都等于 相似比 .
相似比
两个全等的三角形,对应的高、中线、角平分线也相等.两个相似三角形,对应的高、中线、角平分线之比等于相似比.
相似三角形的周长之比与面积之比
阅读课本“思考”至“例1”前的内容,完成下面的问题.
1.如果△ABC∽△A'B'C',且相似比为k,那么=== k ,由等比性质,得= k .
k
k
2.如果△ABC∽△A'B'C',且相似比为k,AD、A'D'是对应高,则由三角形的面积公式及定理1,可得==·= k2 .
归纳总结 定理2:相似三角形周长的比等于 相似比 .
定理3:相似三角形面积的比等于 相似比的平方 .
k2
相似比
相似比的平方
让学生经历以上的证明过程,使其理解定理,形成一种对知识规律的认知,往往效果要比死记硬背好得多.
·导学建议·
1.若△AB C∽△AB'C,且面积比为4∶9,则其对应边上的高的比为 ( C )
A. B. C. D.
2.已知△ABC的三边分别是5,6,7,与它相似△A'B'C'的最短边为10,则△A'B'C'的周长是 36 .
C
36
1.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=5 m,点P到CD的距离是3 m,则P到AB的距离是 ( C )
A. m B. m
C. m D. m
C
2.△ABC与△A1B1C1是相似三角形,且=2,S△ABC=9,则= 36 .
36
3.已知一个三角形的三边长分别是1,2,3,与其相似的三角形的最大边长为3,求较大三角形的周长.
解:∵边长分别是1,2,3的三角形的最大边为3,小于另一
三角形的最大边3,
∴这个三角形的周长等于1+2+3=4+2,
∴它与另一三角形的相似比=3∶3=1∶,
它与另一三角形的周长的比也为1∶,
∴另一三角形的周长=(4+2)×=4+4.
方法归纳交流 利用相似三角形的性质求三角形的周长或面积,一般要知道 相似比 和其中一个三角形的 周长 或 面积 .
相似比
周长
面
积
4.如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求平行四边形ABCD的面积.
解:(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∴∠ABF=∠CEB,
∴△ABF∽△CEB.
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB平行且等于CD,
∴△DEF∽△CEB,△DEF∽△ABF.
∵DE=CD,
∴=2=,=2=.
∵S△DEF=2,
∴S△CEB=18,S△ABF=8.
∵S四边形BCDF=S△BCE-S△DEF=16,
∴S四边形ABCD=S四边形BCDF+S△ABF=16+8=24.
1.如果两个相似三角形的面积之比为9∶4,那么这两个三角形的周长之比为 ( D )
A.81∶16 B.27∶12
C.9∶4 D.3∶2
D
2.如图,李老师用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上,已知直角三角形纸板中DE=16 cm,EF=12 cm,测得眼睛D离地面的高度为1.8米,他与“步云阁”的水平距距离CD为104 m,则“步云阁”的高度AB是 ( C )
A.75.5 m B.77.1 m
C.79.8 m D.82.5 m
C
3.已知△ABC∽△DEF,且相似比为2∶3,则下列说法中正确的结论是 ①④ .
①对应中线之比为2∶3;②对应角平分线之比为3∶2;③△ABC与△DEF的周长之比为4∶9;④△ABC与△DEF的面积之比为4∶9.
①④
如图,直角三角形的铁片ABC的两直角边BC、AC的长分别为3 cm和4 cm,分别采用(1)、(2)两种剪法,剪出一块正方形铁片,为使所得的正方形面积最大,问哪一种剪法好?为什么?
解:如图(1),设图中正方形的边长为x cm,则AD=(4-x)cm.
∵DE∥BC,∴=,∴=,
解得x=.
如图(2),设图中正方形的边长为y cm.
∵CH= cm,又△CDE∽△CAB,∴=,
∴=,∴y=.
∵>,∴图(1)中的剪法好.
