四川省绵阳南山名校2023-2024学年高一上学期12月月考数学试题(含答案)
文档属性
| 名称 | 四川省绵阳南山名校2023-2024学年高一上学期12月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 209.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 19:33:02 | ||
图片预览



文档简介
绵阳南山中学实验学校高2023级高一(上)12月月考
数学试题
注意事项:
1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2 . 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3. 考试结束后,将答题卡交回。
一、单项选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.( )
A.- B. C. D.-
2.设全集,则图中阴影部分对应的集合是( )
A. B.
C. D.
3.下列与函数是同一个函数的是( )
A. B. C. D.
4.已知,,则角的终边位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知p:,q:,若p是q的充分不必要条件,则m的取值范围是( )
A. B. C. D.
6.我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔离分家万事休.”在数学学习和研究中,常用函数的图象来研究函数性质,也常用函数解析式来琢磨函数的图象特征,函数的大致图象是( )
A. B.
C. D.
7.已知函数是偶函数,当时,恒成立,设,,,则的大小关系为( )
A. B. C. D.
8.中国的技术世界领先,其数学原理之一便是著名的香农公式:.它表示:在受噪声干扰的信道中,最大信息传递速率(单位:)取决于信道宽度(单位:) 信道内信号的平均功率(单位:)、信道内部的高斯噪声功率(单位:)的大小,其中叫做信噪比,按照香农公式,若信道宽度变为原来倍,而将信噪比从提升至,则大约增加了( )(附:)
A. B. C. D.
二、多选题(本题共 4 小题,每小题5 分,共 20 分。在每小题给出的四个选项中,有多项是符合题目要求。全部选对的得 5 分,部分选对的得 2 分,有选错的得 0 分)
9.下列命题正确的是( )
A.的角与角终边重合
B.命题“”的否定是“”
C.已知,且满足.则的最小值为16
D.关于的一元二次不等式的解集为,则=3
10.若扇形周长为36,当这个扇形面积最大时,下列结论正确的是( )
扇形的圆心角为2rad B.扇形的弧长为18
C.扇形的半径为9 D.扇形圆心角所对弦长为
11.已知函数(且),若,则使不等式成立的解可能是( )
A.-1 B.1
C. D.3
已知函数,则下列选项正确的是( )
A.在上单调递增 B.在上单调递减
C.存在最大值 D.图像关于对称
三、填空题(本题共 4 小题,每小题5 分,共 20 分)
13.函数 的定义域是 .
14.已知角的顶点在坐标原点,始边与x轴的非负半轴重合,终边过点,则 .
15.已知幂函数在上单调递增,当时,方程有两个不同的实数解,则的取值范围是 .
16.已知函数,若函数有两个零点,且,则的取值范围为 .
四、解答题(本题共 6小题,共70 分。解答题应写出文字说明、证明过程或演算步骤)
17.(10分)计算:
(1)
18.(12分)已知集合,或.
(1)当时,求;
(2)在①,②,③这三个条件中任选一个,补充在(2)问中的横线上,并求解,若__________,求实数的取值范围.
(注:如果选择多个条件分别解答,按第一个解答计分)
19.(12分)已知,求下列各式的值.
(1)若 2,求 的值;
(2)若,求的值.
20.(12分)设,
(1)若的解集为R,求实数的取值范围;
(2)解关于的不等式.
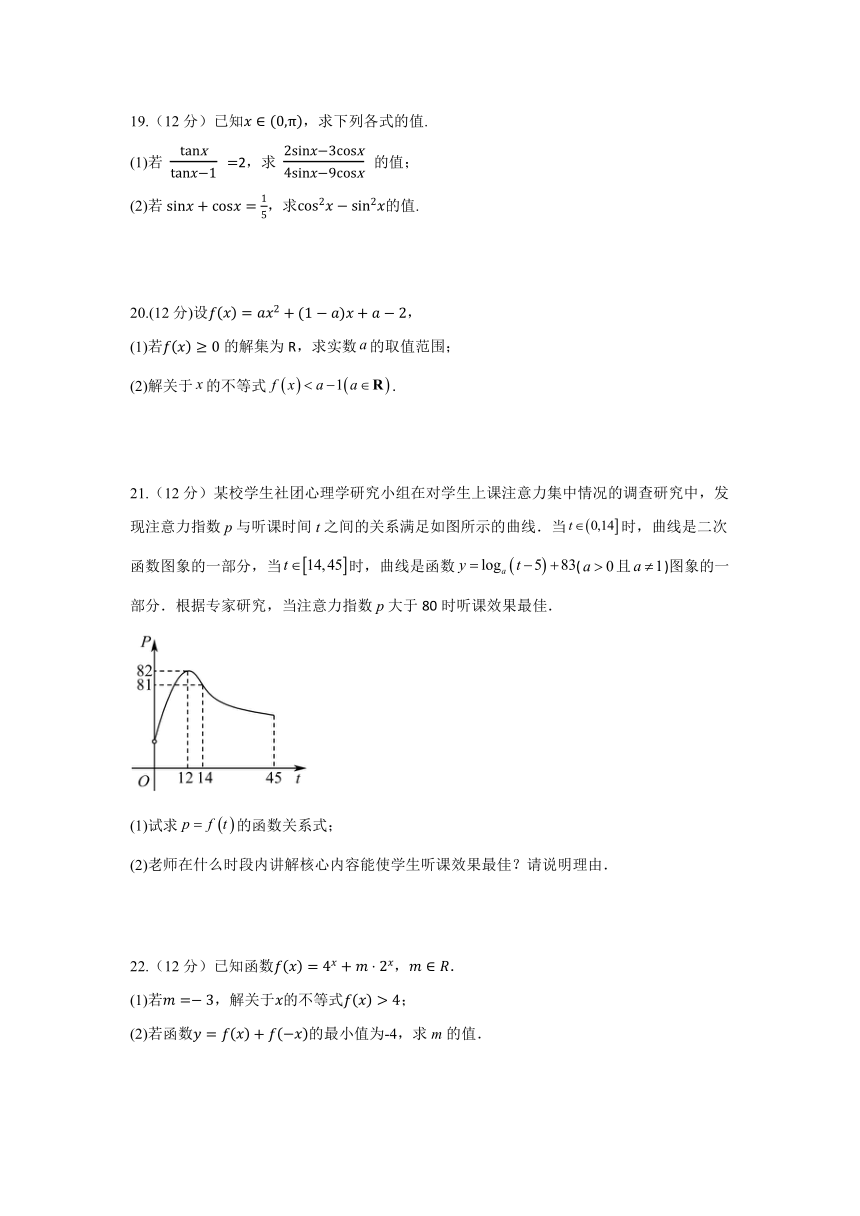
21.(12分)某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现注意力指数p与听课时间t之间的关系满足如图所示的曲线.当时,曲线是二次函数图象的一部分,当时,曲线是函数(且)图象的一部分.根据专家研究,当注意力指数p大于80时听课效果最佳.
(1)试求的函数关系式;
(2)老师在什么时段内讲解核心内容能使学生听课效果最佳?请说明理由.
22.(12分)已知函数,.
(1)若,解关于的不等式;
(2)若函数的最小值为-4,求m的值.
绵阳南山中学实验学校高2023级高一(上)12月月考
数学试题答案
一.单选题:1-8 ACDDCBCD
二.多选题:9.ABD 10. ABC 11. BCD 12. CD
三.填空题:13. 14. 2 15. 16.
16.的零点等价于与交点的横坐标,易知在定义域上单调递减,结合一次函数性质可得如下函数图象,
故,,
所以①,
令,则①=,
由二次函数的性质可知当时取得最小值,没有最大值,
故.故答案为:.
四.解答题:
17.(1)原式=. (5分)
(2)原式=
(10分)
(1)解:当时,,
或,所以,,(3分)
因此,. (5分)
(2)解:若选①,当时,则时,即当时,成立,(7分)
当时,即当时,即当时, (8分)
由可得,解得,此时. (10分)
综上,; (12分)
若选②,当时,则时,即当时,成立,(7分)
当时,即当时,即当时,(8分)
由可得,解得,此时. (10分)
综上,; (12分)
若选③,由可得, (7分)
当时,则时,即当时,成立,(8分)
当时,即当时,即当时,
由可得,解得,此时. (10分)
综上,. (12分)
19.(1)由于,所以, (2分)
所以原式= (4分)
. (6分)
(2)将已知等式,
两边平方得:,
即, (8分)
∴, (9分)
∵,∴,即,
∴, (11分)
∴. (12分)
20.(1),若的解集为R,则不等式在R上恒成立
①当时,不恒成立. (2分)
②当恒成立等价于解得. (5分)
综上:当时,不等式的解集为R; (6分)
(2)不等式,等价于.
当时,不等式可化为,所以不等式的解集为; (7分)
当时,不等式可化为,此时,
所以不等式的解集为; (8分)
当时,不等式可化为,
①当时,,不等式的解集为;(9分)
②当时,,不等式的解集为或;(10分)
③当时,,不等式的解集为或.(11分)
综上:当时,等式的解集为或;
当时,不等式的解集为;
当时,不等式的解集为或;
当时,不等式的解集为;
当时,不等式的解集为. (12分)
21.(1)由题意知,当时,曲线是二次函数图象的一部分,
抛物线顶点坐标为,且曲线过点,
设二次函数为,则,解得,
则可得,. (2分)
又当时,曲线是函数(且)图象的一部分,
且曲线过点,则,即,解得,
则,. (5分)
则. (6分)
(2)由题意知,注意力指数p大于80时听课效果最佳,
当时,令,
解得:. (8分)
当时,令,
解得:. (10分)
综上可得,.
故老师在这一时间段内讲解核心内容,学生听课效果最佳.(12分)
22.(1)时,由得,
,, (2分)
因为,所以,解得,
所以原不等式的解集为. (4分)
因为
,
令,因为,
所以,(当且仅当时取得等号) (6分)
则,, (7分)
①当,即时,在上单调递增,
当,即时,,
所以,解得,符合题意; (9分)
②当,即时,
在上单调递减,在上单调递增,
当,,
所以,解得,不合题意,舍去. (11分)
综上,的值为-3. (12分)
数学试题
注意事项:
1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2 . 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3. 考试结束后,将答题卡交回。
一、单项选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.( )
A.- B. C. D.-
2.设全集,则图中阴影部分对应的集合是( )
A. B.
C. D.
3.下列与函数是同一个函数的是( )
A. B. C. D.
4.已知,,则角的终边位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知p:,q:,若p是q的充分不必要条件,则m的取值范围是( )
A. B. C. D.
6.我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔离分家万事休.”在数学学习和研究中,常用函数的图象来研究函数性质,也常用函数解析式来琢磨函数的图象特征,函数的大致图象是( )
A. B.
C. D.
7.已知函数是偶函数,当时,恒成立,设,,,则的大小关系为( )
A. B. C. D.
8.中国的技术世界领先,其数学原理之一便是著名的香农公式:.它表示:在受噪声干扰的信道中,最大信息传递速率(单位:)取决于信道宽度(单位:) 信道内信号的平均功率(单位:)、信道内部的高斯噪声功率(单位:)的大小,其中叫做信噪比,按照香农公式,若信道宽度变为原来倍,而将信噪比从提升至,则大约增加了( )(附:)
A. B. C. D.
二、多选题(本题共 4 小题,每小题5 分,共 20 分。在每小题给出的四个选项中,有多项是符合题目要求。全部选对的得 5 分,部分选对的得 2 分,有选错的得 0 分)
9.下列命题正确的是( )
A.的角与角终边重合
B.命题“”的否定是“”
C.已知,且满足.则的最小值为16
D.关于的一元二次不等式的解集为,则=3
10.若扇形周长为36,当这个扇形面积最大时,下列结论正确的是( )
扇形的圆心角为2rad B.扇形的弧长为18
C.扇形的半径为9 D.扇形圆心角所对弦长为
11.已知函数(且),若,则使不等式成立的解可能是( )
A.-1 B.1
C. D.3
已知函数,则下列选项正确的是( )
A.在上单调递增 B.在上单调递减
C.存在最大值 D.图像关于对称
三、填空题(本题共 4 小题,每小题5 分,共 20 分)
13.函数 的定义域是 .
14.已知角的顶点在坐标原点,始边与x轴的非负半轴重合,终边过点,则 .
15.已知幂函数在上单调递增,当时,方程有两个不同的实数解,则的取值范围是 .
16.已知函数,若函数有两个零点,且,则的取值范围为 .
四、解答题(本题共 6小题,共70 分。解答题应写出文字说明、证明过程或演算步骤)
17.(10分)计算:
(1)
18.(12分)已知集合,或.
(1)当时,求;
(2)在①,②,③这三个条件中任选一个,补充在(2)问中的横线上,并求解,若__________,求实数的取值范围.
(注:如果选择多个条件分别解答,按第一个解答计分)
19.(12分)已知,求下列各式的值.
(1)若 2,求 的值;
(2)若,求的值.
20.(12分)设,
(1)若的解集为R,求实数的取值范围;
(2)解关于的不等式.
21.(12分)某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现注意力指数p与听课时间t之间的关系满足如图所示的曲线.当时,曲线是二次函数图象的一部分,当时,曲线是函数(且)图象的一部分.根据专家研究,当注意力指数p大于80时听课效果最佳.
(1)试求的函数关系式;
(2)老师在什么时段内讲解核心内容能使学生听课效果最佳?请说明理由.
22.(12分)已知函数,.
(1)若,解关于的不等式;
(2)若函数的最小值为-4,求m的值.
绵阳南山中学实验学校高2023级高一(上)12月月考
数学试题答案
一.单选题:1-8 ACDDCBCD
二.多选题:9.ABD 10. ABC 11. BCD 12. CD
三.填空题:13. 14. 2 15. 16.
16.的零点等价于与交点的横坐标,易知在定义域上单调递减,结合一次函数性质可得如下函数图象,
故,,
所以①,
令,则①=,
由二次函数的性质可知当时取得最小值,没有最大值,
故.故答案为:.
四.解答题:
17.(1)原式=. (5分)
(2)原式=
(10分)
(1)解:当时,,
或,所以,,(3分)
因此,. (5分)
(2)解:若选①,当时,则时,即当时,成立,(7分)
当时,即当时,即当时, (8分)
由可得,解得,此时. (10分)
综上,; (12分)
若选②,当时,则时,即当时,成立,(7分)
当时,即当时,即当时,(8分)
由可得,解得,此时. (10分)
综上,; (12分)
若选③,由可得, (7分)
当时,则时,即当时,成立,(8分)
当时,即当时,即当时,
由可得,解得,此时. (10分)
综上,. (12分)
19.(1)由于,所以, (2分)
所以原式= (4分)
. (6分)
(2)将已知等式,
两边平方得:,
即, (8分)
∴, (9分)
∵,∴,即,
∴, (11分)
∴. (12分)
20.(1),若的解集为R,则不等式在R上恒成立
①当时,不恒成立. (2分)
②当恒成立等价于解得. (5分)
综上:当时,不等式的解集为R; (6分)
(2)不等式,等价于.
当时,不等式可化为,所以不等式的解集为; (7分)
当时,不等式可化为,此时,
所以不等式的解集为; (8分)
当时,不等式可化为,
①当时,,不等式的解集为;(9分)
②当时,,不等式的解集为或;(10分)
③当时,,不等式的解集为或.(11分)
综上:当时,等式的解集为或;
当时,不等式的解集为;
当时,不等式的解集为或;
当时,不等式的解集为;
当时,不等式的解集为. (12分)
21.(1)由题意知,当时,曲线是二次函数图象的一部分,
抛物线顶点坐标为,且曲线过点,
设二次函数为,则,解得,
则可得,. (2分)
又当时,曲线是函数(且)图象的一部分,
且曲线过点,则,即,解得,
则,. (5分)
则. (6分)
(2)由题意知,注意力指数p大于80时听课效果最佳,
当时,令,
解得:. (8分)
当时,令,
解得:. (10分)
综上可得,.
故老师在这一时间段内讲解核心内容,学生听课效果最佳.(12分)
22.(1)时,由得,
,, (2分)
因为,所以,解得,
所以原不等式的解集为. (4分)
因为
,
令,因为,
所以,(当且仅当时取得等号) (6分)
则,, (7分)
①当,即时,在上单调递增,
当,即时,,
所以,解得,符合题意; (9分)
②当,即时,
在上单调递减,在上单调递增,
当,,
所以,解得,不合题意,舍去. (11分)
综上,的值为-3. (12分)
同课章节目录
