4.3.2等比数列的前n项和公式 课件(共33张PPT)
文档属性
| 名称 | 4.3.2等比数列的前n项和公式 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 20:39:48 | ||
图片预览









文档简介
(共33张PPT)
4.3.2 等比数列的前n项和公式
学习目标 核心素养
1.探索等比数列的前n项和公式的推导方法,掌握“错位相减法”的操作步骤。(重点) 2.掌握等比数列的前n项和公式并解决有关计算问题。(重点) 3.运用等比数列的前n项和公式解决一些简单的实际问题。(难点) 1.探究等比数列的前n项和公式的推导过程,培养逻辑推理、数学抽象素养。
2.通过等比数列的前n项和公式的运用,培养数学运算素养。
3.借助等比数列的前n项和公式解决简单的实际问题,培养数学建模素养。
目标与素养
数学小故事
相传,古印度的国王打算重赏国际象棋的发明者——宰相西萨。问他想要什么。于是,这位宰相跪在国王面前说:
新课导入
思考:
问题1: 构成什么数列?
麦粒总数为
问题2:这位聪明的宰相到底要多少麦粒呢?
首项为1,公比为2的等比数列
4.3.2 等比数列的前n项和公式
如何求一个等比数列的前n项和?
合作探究:
①
等比数列前n项和公式:
注意
(1)等比数列求和时,应考虑q=1与q≠1两种情况.
(2)推导等比数列前n项和公式的方法:错位相减法.
探究新知:
(3)
判断对错
n个
5n
反思总结:
用公式前,先弄清楚首项 、公比 、项数
小试牛刀
呼应故事
1000粒麦子的质量约为40g
麦粒的总质量超过了7000亿吨
约是2016-2017年度世界小麦产量的981倍,因此,国王根本不可能实现他的诺言。
冲动是魔鬼!
启示:这个故事告诉我们
数学来源于生活,又高于生活!
学好数学!学会理性思考!
典例分析
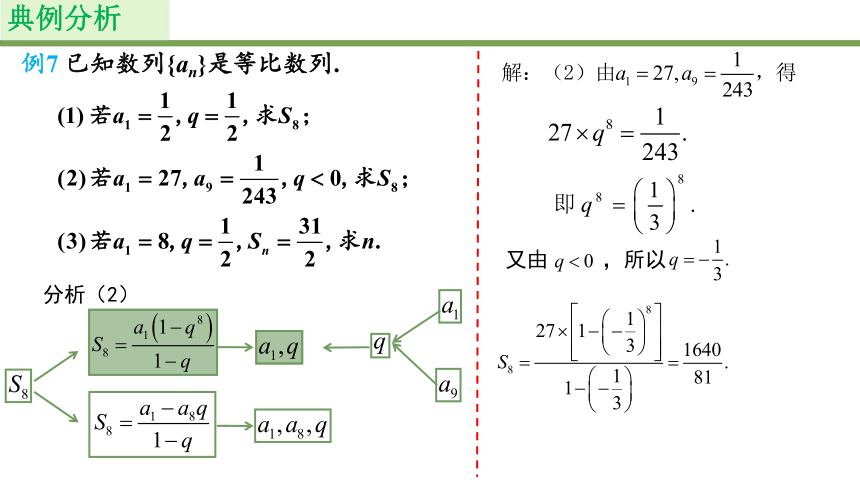
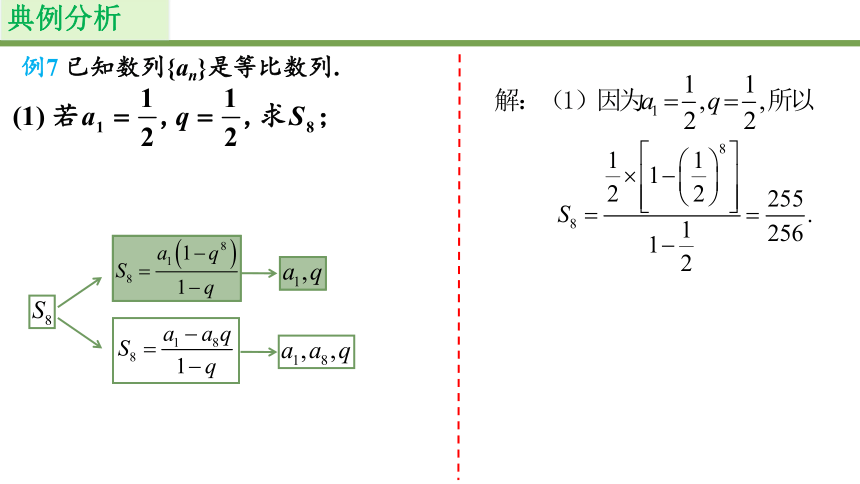
例7 已知数列{an}是等比数列.
分析(2)
又由 ,所以
知识应用
典例分析
例7 已知数列{an}是等比数列.
典例分析
例7 已知数列{an}是等比数列.
分析(3)
整理,得
解得
归纳总结
对于等比数列的相关量 已知几个量就可以确定其他量?
(1)若 求 ;
(2)若 求 ;
(3)若 求 .
基本量法
方程思想
知三求二
典例分析
例8 已知等比数列{an}的首项为-1,前n项和为Sn,若 求公比q.
不要忘记考虑q=1与q≠1两种情况.
当q
总结:若q未知,用公式时要考虑q是否为1
跟踪训练
在等比数列{an}中,设前n项和为Sn,S3=,S6=,求公比q .
典例分析
例9 已知等比数列{an}的公比q ≠ -1,前n项和为Sn,证明 Sn , S2n-Sn , S3n-S2n , 成等比数列,并求这个数列的公比.
例9 已知等比数列{an}的公比q ≠ -1,前n项和为Sn,证明 Sn , S2n-Sn , S3n-S2n , 成等比数列,并这个数列的公比.
前n项和定义法
典例分析
法2:
性质二
解法1:
解法2:
跟踪训练
直击高考
1. 已知数列{an}是等比数列,
系数和常数互为相反数
提示:
3.
直击高考
(4)已知数列{an}的前n项和为Sn=2n-1,求该数列的奇数项的前n项和.
这节课
收获了什么
获取知识的方法
知识内容
思想、素养
课堂小结
课堂小结
数学思想:
转化和化归
数学知识:
错位相减法
数学方法:
方程思想
等比数列的前n项和公式
分类讨论思想
数学素养:
逻辑推理、数学抽象素养、数学运算、数学建模
布置作业
1.必做题:课后达标前10道,
选做题:第11.12题。
2.查阅相关资料,了解中国古代数学家求数列和的方法。
如何求一个等比数列的前n项和?
探究新知:
①
②
①-②得:
①×q 得
讨论公比q是否为1
错位
相减
分类讨论思想
使用公式求和时,若公比q不确定需注意对 q=1 和 q≠1 的情况加以讨论。
跟踪训练
公式探究
追问6 求和的根本目的是什么?
消除项与项之间的差异
消除中间项
答案:
利用公差
小结
前n项和公式
或
错位相减
乘公比
分类讨论
q≠1,q=1
等比数列
知三求二
4. 已知三个数成等比数列,它们的和等于14,积等于64. 求这个等比数列的首项和公比.
课本P37
5. 如果一个等比数列前5项的和等于10,前10项的和等于50,那么这个数列的公比等于多少
课本P37
4.3.2 等比数列的前n项和公式
学习目标 核心素养
1.探索等比数列的前n项和公式的推导方法,掌握“错位相减法”的操作步骤。(重点) 2.掌握等比数列的前n项和公式并解决有关计算问题。(重点) 3.运用等比数列的前n项和公式解决一些简单的实际问题。(难点) 1.探究等比数列的前n项和公式的推导过程,培养逻辑推理、数学抽象素养。
2.通过等比数列的前n项和公式的运用,培养数学运算素养。
3.借助等比数列的前n项和公式解决简单的实际问题,培养数学建模素养。
目标与素养
数学小故事
相传,古印度的国王打算重赏国际象棋的发明者——宰相西萨。问他想要什么。于是,这位宰相跪在国王面前说:
新课导入
思考:
问题1: 构成什么数列?
麦粒总数为
问题2:这位聪明的宰相到底要多少麦粒呢?
首项为1,公比为2的等比数列
4.3.2 等比数列的前n项和公式
如何求一个等比数列的前n项和?
合作探究:
①
等比数列前n项和公式:
注意
(1)等比数列求和时,应考虑q=1与q≠1两种情况.
(2)推导等比数列前n项和公式的方法:错位相减法.
探究新知:
(3)
判断对错
n个
5n
反思总结:
用公式前,先弄清楚首项 、公比 、项数
小试牛刀
呼应故事
1000粒麦子的质量约为40g
麦粒的总质量超过了7000亿吨
约是2016-2017年度世界小麦产量的981倍,因此,国王根本不可能实现他的诺言。
冲动是魔鬼!
启示:这个故事告诉我们
数学来源于生活,又高于生活!
学好数学!学会理性思考!
典例分析
例7 已知数列{an}是等比数列.
分析(2)
又由 ,所以
知识应用
典例分析
例7 已知数列{an}是等比数列.
典例分析
例7 已知数列{an}是等比数列.
分析(3)
整理,得
解得
归纳总结
对于等比数列的相关量 已知几个量就可以确定其他量?
(1)若 求 ;
(2)若 求 ;
(3)若 求 .
基本量法
方程思想
知三求二
典例分析
例8 已知等比数列{an}的首项为-1,前n项和为Sn,若 求公比q.
不要忘记考虑q=1与q≠1两种情况.
当q
总结:若q未知,用公式时要考虑q是否为1
跟踪训练
在等比数列{an}中,设前n项和为Sn,S3=,S6=,求公比q .
典例分析
例9 已知等比数列{an}的公比q ≠ -1,前n项和为Sn,证明 Sn , S2n-Sn , S3n-S2n , 成等比数列,并求这个数列的公比.
例9 已知等比数列{an}的公比q ≠ -1,前n项和为Sn,证明 Sn , S2n-Sn , S3n-S2n , 成等比数列,并这个数列的公比.
前n项和定义法
典例分析
法2:
性质二
解法1:
解法2:
跟踪训练
直击高考
1. 已知数列{an}是等比数列,
系数和常数互为相反数
提示:
3.
直击高考
(4)已知数列{an}的前n项和为Sn=2n-1,求该数列的奇数项的前n项和.
这节课
收获了什么
获取知识的方法
知识内容
思想、素养
课堂小结
课堂小结
数学思想:
转化和化归
数学知识:
错位相减法
数学方法:
方程思想
等比数列的前n项和公式
分类讨论思想
数学素养:
逻辑推理、数学抽象素养、数学运算、数学建模
布置作业
1.必做题:课后达标前10道,
选做题:第11.12题。
2.查阅相关资料,了解中国古代数学家求数列和的方法。
如何求一个等比数列的前n项和?
探究新知:
①
②
①-②得:
①×q 得
讨论公比q是否为1
错位
相减
分类讨论思想
使用公式求和时,若公比q不确定需注意对 q=1 和 q≠1 的情况加以讨论。
跟踪训练
公式探究
追问6 求和的根本目的是什么?
消除项与项之间的差异
消除中间项
答案:
利用公差
小结
前n项和公式
或
错位相减
乘公比
分类讨论
q≠1,q=1
等比数列
知三求二
4. 已知三个数成等比数列,它们的和等于14,积等于64. 求这个等比数列的首项和公比.
课本P37
5. 如果一个等比数列前5项的和等于10,前10项的和等于50,那么这个数列的公比等于多少
课本P37
