2.6.2 解一元一次不等式组(2) 课件(共19张PPT)
文档属性
| 名称 | 2.6.2 解一元一次不等式组(2) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 507.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 09:14:30 | ||
图片预览




文档简介
(共19张PPT)
第2章 一元一次不等式与 一元一次不等式组
2.6 一元一次不等式组
第2课时 解一元一次不等式组(2)
1.能够解稍复杂的一元一次不等式组
2.能够挖掘具体问题中的数量关系,列不等式组并解决问题
1.稍复杂一元一次不等式组的解法
2.用一元一次不等式组解决实际问题
教学目标
重难点
温故知新
在什么条件下,长度为 3 cm,7 cm,x cm 的三条线段可以围成一个三角形?
3 cm
7 cm
温故知新
解:三角形三边关系可得,
3 + x > 7,①
x- 3 < 7. ②
解不等式①,得 x > 4.
解不等式②,得 x < 10.
所以原不等式组的解集为4 < x < 10.
典型例题
解:解不等式①,得
x<-2.
解不等式②,得
x>3.
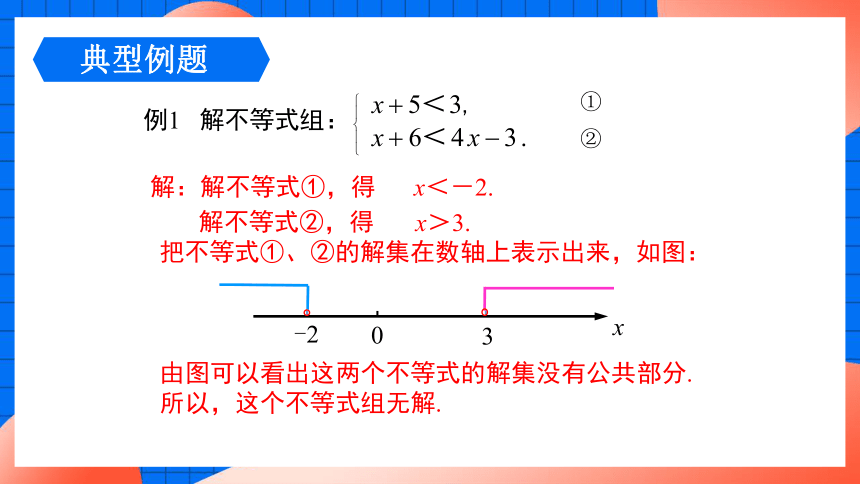
例1 解不等式组:
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
x
典型例题
例2 解不等式组:
3x – 2 < x + 1, ①
x + 5 > 4x + 1. ②
解:解不等式①,得 x < .
解不等式②,得 x < .
在同一条数轴上表示不等式①②的解集,如图
-3
-2
-1
0
1
2
所以原不等式组的解集为 x < .
典型例题
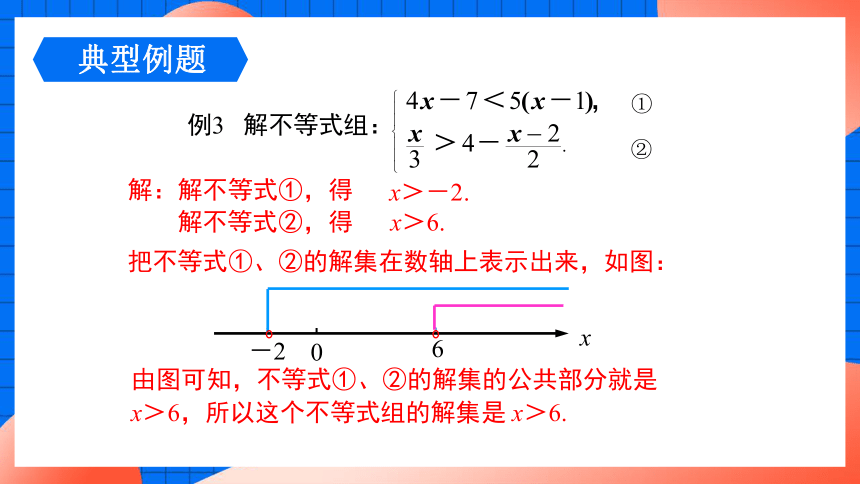
例3 解不等式组:
①
②
解:解不等式①,得
x>-2.
解不等式②,得
x>6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是 x>6.
x
求不等式组的解集一定要先求出不等式组中每个不等式的解集,再求出这些不等式的解集的公共部分,而不能仿照解方程组的方法直接把两个不等式相加(或相减)得出其解集,从而导致错误.
注意事项
小牛试刀
解下列不等式组:
【分析】分别求出①②的解集,再找出不等式组的解集.
解:(1)解不等式①,得x<1.
解不等式②,得x>-4.
所以原不等式组的解集是-4<x<1;
解:(2)解不等式①,得x<2.
解不等式②,得x>3.
所以原不等式组无解.
应用实践
把一堆苹果分给几个小孩,如果每人分3个,则余8个;如果每人分5个,则最后一人得到的苹果数不足3个,求小孩的人数和苹果的个数.
提示:“不足3个”的意思是“大于或等于1个且小于3个”.
应用实践
解:设有x个小孩,则有苹果(3x + 8)个.
根据题意,得 1 ≤ 3x + 8 - 5(x - 1) < 3,
3x + 8 - 5(x - 1) < 3,
1 ≤ 3x + 8 - 5(x - 1) .
即
解得 5 < x ≤ 6.
因为x为正整数,所以 x = 6,3x + 8 = 26.
答:有6个小孩,26个苹果.
总结方法
利用一元一次不等式组解决实际问题,关键是找出题中的两个或两个以上的不等关系,列出不等式组并求解,还需要根据实际情况确定实际问题的最终答案.
巩固提高
因为 x 只能取整数,所以 x=6,即有 6 辆汽车运这批货物.
用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空. 请你算一算:有多少辆汽车运这批货物?
解:设有 x 辆汽车,则这批货物共有 (4x+20 ) t.
依题意得
解得 5<x <7.
随堂练习
1.如图,数轴上表示的解集用不等式表示为( )
A.2<x<4 B.-2<x≤4
C.-2≤x<4 D.-2≤x≤4
B
3
2.不等式 的正整数解为____.
随堂练习
3. 解下列不等式组:
解:(1) 1< x <5.
(2) -4< x ≤1.
随堂练习
4.一个人的头发大约有10万根到20万根,每根头发每天大约生长0.32 mm,小颖的头发现在大约有10 cm长,那么大约经过多长时间,她的头发才能生长到16 cm到28 cm
【分析】这个问题中的不等关系是小颖若干天后的头发在16 cm到28 cm之间,即16 cm≤小颖若干天后的头发长度≤28 cm.
解:设大约经过x天后,小颖头发生长到16 cm到28 cm.
16×10≤100+0.32x≤28×10.
解这个不等式组,得187.5≤x≤562.5.
因此,大约需要188天到562天,小颖的头发才能生长到16 cm到28 cm.
课堂小结
一元一次不等式组
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
→
实际应用(特殊解)
→
课后作业
完成教材第59页习题2.9第1题.
这节课你学到了什么?谈谈你的收获,
小结与反思
第2章 一元一次不等式与 一元一次不等式组
2.6 一元一次不等式组
第2课时 解一元一次不等式组(2)
1.能够解稍复杂的一元一次不等式组
2.能够挖掘具体问题中的数量关系,列不等式组并解决问题
1.稍复杂一元一次不等式组的解法
2.用一元一次不等式组解决实际问题
教学目标
重难点
温故知新
在什么条件下,长度为 3 cm,7 cm,x cm 的三条线段可以围成一个三角形?
3 cm
7 cm
温故知新
解:三角形三边关系可得,
3 + x > 7,①
x- 3 < 7. ②
解不等式①,得 x > 4.
解不等式②,得 x < 10.
所以原不等式组的解集为4 < x < 10.
典型例题
解:解不等式①,得
x<-2.
解不等式②,得
x>3.
例1 解不等式组:
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
x
典型例题
例2 解不等式组:
3x – 2 < x + 1, ①
x + 5 > 4x + 1. ②
解:解不等式①,得 x < .
解不等式②,得 x < .
在同一条数轴上表示不等式①②的解集,如图
-3
-2
-1
0
1
2
所以原不等式组的解集为 x < .
典型例题
例3 解不等式组:
①
②
解:解不等式①,得
x>-2.
解不等式②,得
x>6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是 x>6.
x
求不等式组的解集一定要先求出不等式组中每个不等式的解集,再求出这些不等式的解集的公共部分,而不能仿照解方程组的方法直接把两个不等式相加(或相减)得出其解集,从而导致错误.
注意事项
小牛试刀
解下列不等式组:
【分析】分别求出①②的解集,再找出不等式组的解集.
解:(1)解不等式①,得x<1.
解不等式②,得x>-4.
所以原不等式组的解集是-4<x<1;
解:(2)解不等式①,得x<2.
解不等式②,得x>3.
所以原不等式组无解.
应用实践
把一堆苹果分给几个小孩,如果每人分3个,则余8个;如果每人分5个,则最后一人得到的苹果数不足3个,求小孩的人数和苹果的个数.
提示:“不足3个”的意思是“大于或等于1个且小于3个”.
应用实践
解:设有x个小孩,则有苹果(3x + 8)个.
根据题意,得 1 ≤ 3x + 8 - 5(x - 1) < 3,
3x + 8 - 5(x - 1) < 3,
1 ≤ 3x + 8 - 5(x - 1) .
即
解得 5 < x ≤ 6.
因为x为正整数,所以 x = 6,3x + 8 = 26.
答:有6个小孩,26个苹果.
总结方法
利用一元一次不等式组解决实际问题,关键是找出题中的两个或两个以上的不等关系,列出不等式组并求解,还需要根据实际情况确定实际问题的最终答案.
巩固提高
因为 x 只能取整数,所以 x=6,即有 6 辆汽车运这批货物.
用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空. 请你算一算:有多少辆汽车运这批货物?
解:设有 x 辆汽车,则这批货物共有 (4x+20 ) t.
依题意得
解得 5<x <7.
随堂练习
1.如图,数轴上表示的解集用不等式表示为( )
A.2<x<4 B.-2<x≤4
C.-2≤x<4 D.-2≤x≤4
B
3
2.不等式 的正整数解为____.
随堂练习
3. 解下列不等式组:
解:(1) 1< x <5.
(2) -4< x ≤1.
随堂练习
4.一个人的头发大约有10万根到20万根,每根头发每天大约生长0.32 mm,小颖的头发现在大约有10 cm长,那么大约经过多长时间,她的头发才能生长到16 cm到28 cm
【分析】这个问题中的不等关系是小颖若干天后的头发在16 cm到28 cm之间,即16 cm≤小颖若干天后的头发长度≤28 cm.
解:设大约经过x天后,小颖头发生长到16 cm到28 cm.
16×10≤100+0.32x≤28×10.
解这个不等式组,得187.5≤x≤562.5.
因此,大约需要188天到562天,小颖的头发才能生长到16 cm到28 cm.
课堂小结
一元一次不等式组
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
→
实际应用(特殊解)
→
课后作业
完成教材第59页习题2.9第1题.
这节课你学到了什么?谈谈你的收获,
小结与反思
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
