线段垂直平分线的性质 课件 (共24张PPT)说课
文档属性
| 名称 | 线段垂直平分线的性质 课件 (共24张PPT)说课 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 21:02:28 | ||
图片预览






文档简介
(共24张PPT)
线段垂直平分线的性质说课课件
第一页,共24页。
说课程序
说教材
说教法学法
说教学过程
第二页,共24页。
1、地位和作用
线段的垂直平分线是人教版八年级上册第十三章第一节轴对称第二课时的内容。 它是在认识了轴对称性的基础上进行的,是今后证明线段相等和直线互相垂直的依据,因此本节课具有承上启下的重要作用。
第三页,共24页。
2、教学目标
(1)知识与技能目标:
能证明、理解线段垂直平分线性质及其判定定理,会运用定理解决相关问题。能用尺规做出线段的垂直平分线。
(2)过程与方法目标:
探索线段的垂直平分线定理,发展学生的几何直觉,培养学生的猜想能力。并通过“做数学”,让学生对猜想进行检验,作出正确判断。
(3)情感态度与价值观:
通过对定理的探究,让学生充分体会合作的快乐,感受学习数学的趣味性,建立学生学习数学的自信心,克服他们“怕数学”这一心理障碍。
第四页,共24页。
3、教学重点和难点
重点:掌握线段垂直平分线的性质和判定定理。能运用这两个定理解决简单的实际问题。
难点:1、利用尺规作已知线段的垂直平分线。 2、能运用线段的垂直平分线的性质解决简单的实际问题
第五页,共24页。
新课标的理念明确指出:“学生是主体,教师是主导”,结合八年级学生具有可塑性大﹑主动尝试﹑追求独立等特征,本节课采用“学生主体性学习”的教学模式,让学生真正成为课堂的主人。
学生在学习过程中主要采用小组合作交流、动手实践、自主探究的学习方法。
第六页,共24页。
在公路L的同侧,有二职中和周嘉小学A、B,镇政府计划在公路边上修建一栋图书馆,使得两个学校的师生都没意见,问图书馆的位置应选在何处?
A
B
(一)创设情境,引入新课。
L
第七页,共24页。
A
B
PA=PB
P1
P1A=P1B
……
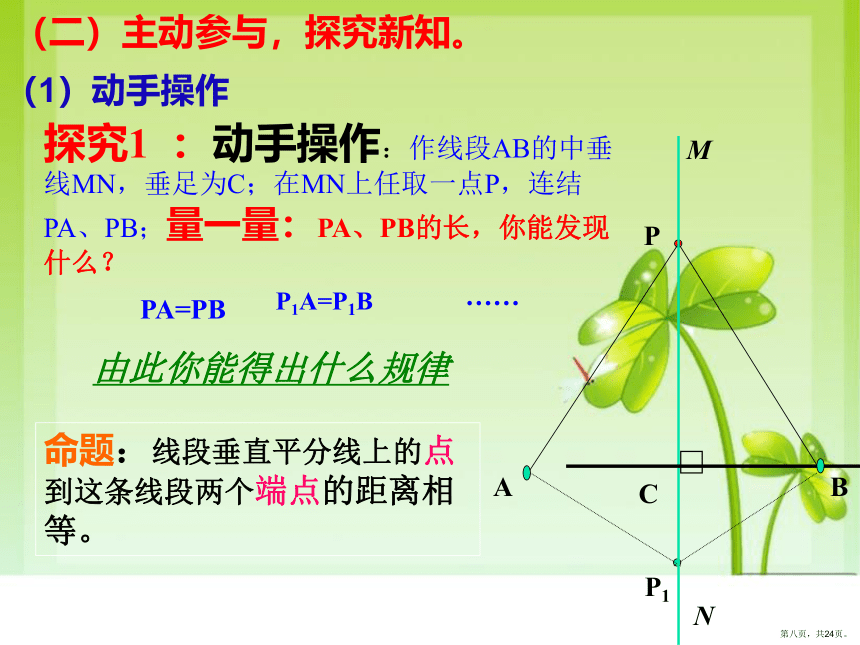
命题:线段垂直平分线上的点到这条线段两个端点的距离相等。
P
M
N
C
探究1 :动手操作:作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得出什么规律
(1)动手操作
(二)主动参与,探究新知。
第八页,共24页。
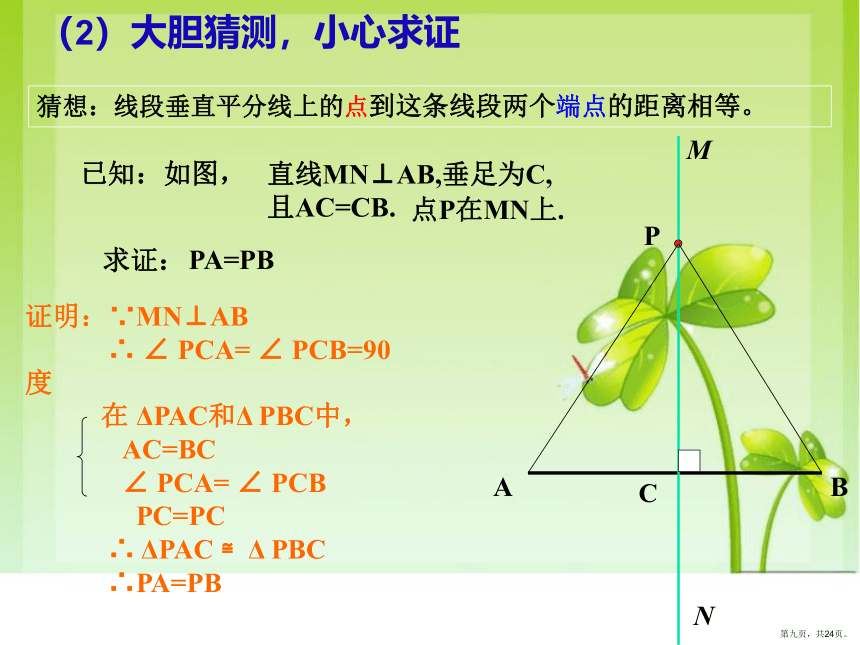
猜想:线段垂直平分线上的点到这条线段两个端点的距离相等。
A
B
P
M
N
C
PA=PB
直线MN⊥AB,垂足为C,
且AC=CB.
已知:如图,
点P在MN上.
求证:
证明:∵MN⊥AB
∴ ∠ PCA= ∠ PCB=90度
在 ΔPAC和Δ PBC中,
AC=BC
∠ PCA= ∠ PCB
PC=PC
∴ ΔPAC ≌Δ PBC
∴PA=PB
(2)大胆猜测,小心求证
第九页,共24页。
A
B
M
N
C
P
动态演示
第十页,共24页。
M
N
C
A
B
Q
第十一页,共24页。
1、如图直线MN垂直平分线段AB,则AE=AF。
第十二页,共24页。
B
A
C
2、求作一点P,使它和已△ABC的三个顶点距离相等.
实际问题
数学化
p
PA=PB=PC
实际问题1
第十三页,共24页。
探究2:性质定理:线段垂直平分线上的点到这条线段两个端点的 距离相等。
A
B
P
M
N
C
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
几何语言叙述:
∵点P在线段AB的垂直平分线上
∴ PA=PB
(2)大胆猜测,小心求证
第十四页,共24页。
A
B
P
C
一、性质定理:线段垂直平分线上的点到这条线段两个端点
的距离相等。
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的
垂直平分线上。
逆命题:
几何语言叙述:
∵PA=PB
∴点P在线段AB的垂直平分线上
(2)大胆猜测,小心求证
第十五页,共24页。
二、逆定理:到线段两个端点距离相等的点,在这条 线段的垂直平分线上。(判定定理)
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
三、 线段的垂直平分线的集合定义: 线段的垂直平分线可以看作是到线段两上端点距离相等的所有点的集合
第十六页,共24页。
例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P在AC的垂直平分线上;
B
A
C
M
N
M’
N’
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
∵PA=PC ∴点P在AC的垂直平分线上
(三)例题示范,形成能力
第十七页,共24页。
例1 已知:如图,在ΔABC中,边AB,BC的垂直平分 线交于P.
求证:点P在AC的垂直平分线上;
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?)
同理 PB=PC.
∴PA=PC.
∴点P在AC的垂直平分线上;
∴AB,BC,AC的垂直平分线相交于点P.
B
A
C
M
N
M’
N’
P
(线段垂直平分线上的点到这条线段两个端点的距离相等).
(到线段两个端点距离相等的点,在这条线段的垂直平分线上)
(三)例题示范,形成能力
第十八页,共24页。
例2、如图,利用尺规作图在直线L上求作一点P,使PA=PB.
L
A
B
实际问题
数学化
实际问题2
p
PA=PB
第十九页,共24页。
1、已知:在ΔABC中,ON是AB的垂直平分线 OA=OC。求证:点O在BC的垂直平分线上。
A
B
C
O
N
(四)巩固达标,学以致用
2、已知:如图,在等腰三角形ABC中,腰AB的垂直平 线MN交AC于点 D,BC=8厘米, ΔBDC的周长20厘米.
求:AB的长.
3、已知:如图,D是BC延长线上的一点,BD=BC+AC.
求证:点C在AD的垂直平分线上.
A
D
M
A
B
C
D
8
第二十页,共24页。
在公路L的同侧,有二职中和周嘉小学A、B,镇政府计划在公路边上修建一栋图书馆,使得两个学校的师生都没意见,问图书馆的位置应选在何处?
A
B
L
第二十一页,共24页。
二、逆定理:到线段两个端点距离相等的点,在这条
线段的垂直平分线上。
一、性质定理:线段垂直平分线上的点到这条线段两个端
点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是到线段两上端点距离相等的所有点的集合
(五)学习小结,知识内化
第二十二页,共24页。
(六)分层作业、能力升华
必做题 学案 1、2、3题
选做题 在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
链接中考(2022 烟台)等腰△ABC中,AB=AC,A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于()A.80° B.70° C.60°D.50°
第二十三页,共24页。
1、线段的垂直平分线的性质:
线段垂直平分线上的点到线段两端点距离相等 即: ∵ MN垂直平分线段AB ∴ AP=BP AQ=BQ AR=BR
2、判定定理:到线段两端距离相等
的点在线段的垂直平分线上。
M
N
(七)版书设计
第二十四页,共24页。
线段垂直平分线的性质说课课件
第一页,共24页。
说课程序
说教材
说教法学法
说教学过程
第二页,共24页。
1、地位和作用
线段的垂直平分线是人教版八年级上册第十三章第一节轴对称第二课时的内容。 它是在认识了轴对称性的基础上进行的,是今后证明线段相等和直线互相垂直的依据,因此本节课具有承上启下的重要作用。
第三页,共24页。
2、教学目标
(1)知识与技能目标:
能证明、理解线段垂直平分线性质及其判定定理,会运用定理解决相关问题。能用尺规做出线段的垂直平分线。
(2)过程与方法目标:
探索线段的垂直平分线定理,发展学生的几何直觉,培养学生的猜想能力。并通过“做数学”,让学生对猜想进行检验,作出正确判断。
(3)情感态度与价值观:
通过对定理的探究,让学生充分体会合作的快乐,感受学习数学的趣味性,建立学生学习数学的自信心,克服他们“怕数学”这一心理障碍。
第四页,共24页。
3、教学重点和难点
重点:掌握线段垂直平分线的性质和判定定理。能运用这两个定理解决简单的实际问题。
难点:1、利用尺规作已知线段的垂直平分线。 2、能运用线段的垂直平分线的性质解决简单的实际问题
第五页,共24页。
新课标的理念明确指出:“学生是主体,教师是主导”,结合八年级学生具有可塑性大﹑主动尝试﹑追求独立等特征,本节课采用“学生主体性学习”的教学模式,让学生真正成为课堂的主人。
学生在学习过程中主要采用小组合作交流、动手实践、自主探究的学习方法。
第六页,共24页。
在公路L的同侧,有二职中和周嘉小学A、B,镇政府计划在公路边上修建一栋图书馆,使得两个学校的师生都没意见,问图书馆的位置应选在何处?
A
B
(一)创设情境,引入新课。
L
第七页,共24页。
A
B
PA=PB
P1
P1A=P1B
……
命题:线段垂直平分线上的点到这条线段两个端点的距离相等。
P
M
N
C
探究1 :动手操作:作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得出什么规律
(1)动手操作
(二)主动参与,探究新知。
第八页,共24页。
猜想:线段垂直平分线上的点到这条线段两个端点的距离相等。
A
B
P
M
N
C
PA=PB
直线MN⊥AB,垂足为C,
且AC=CB.
已知:如图,
点P在MN上.
求证:
证明:∵MN⊥AB
∴ ∠ PCA= ∠ PCB=90度
在 ΔPAC和Δ PBC中,
AC=BC
∠ PCA= ∠ PCB
PC=PC
∴ ΔPAC ≌Δ PBC
∴PA=PB
(2)大胆猜测,小心求证
第九页,共24页。
A
B
M
N
C
P
动态演示
第十页,共24页。
M
N
C
A
B
Q
第十一页,共24页。
1、如图直线MN垂直平分线段AB,则AE=AF。
第十二页,共24页。
B
A
C
2、求作一点P,使它和已△ABC的三个顶点距离相等.
实际问题
数学化
p
PA=PB=PC
实际问题1
第十三页,共24页。
探究2:性质定理:线段垂直平分线上的点到这条线段两个端点的 距离相等。
A
B
P
M
N
C
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
几何语言叙述:
∵点P在线段AB的垂直平分线上
∴ PA=PB
(2)大胆猜测,小心求证
第十四页,共24页。
A
B
P
C
一、性质定理:线段垂直平分线上的点到这条线段两个端点
的距离相等。
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的
垂直平分线上。
逆命题:
几何语言叙述:
∵PA=PB
∴点P在线段AB的垂直平分线上
(2)大胆猜测,小心求证
第十五页,共24页。
二、逆定理:到线段两个端点距离相等的点,在这条 线段的垂直平分线上。(判定定理)
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
三、 线段的垂直平分线的集合定义: 线段的垂直平分线可以看作是到线段两上端点距离相等的所有点的集合
第十六页,共24页。
例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P在AC的垂直平分线上;
B
A
C
M
N
M’
N’
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
∵PA=PC ∴点P在AC的垂直平分线上
(三)例题示范,形成能力
第十七页,共24页。
例1 已知:如图,在ΔABC中,边AB,BC的垂直平分 线交于P.
求证:点P在AC的垂直平分线上;
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?)
同理 PB=PC.
∴PA=PC.
∴点P在AC的垂直平分线上;
∴AB,BC,AC的垂直平分线相交于点P.
B
A
C
M
N
M’
N’
P
(线段垂直平分线上的点到这条线段两个端点的距离相等).
(到线段两个端点距离相等的点,在这条线段的垂直平分线上)
(三)例题示范,形成能力
第十八页,共24页。
例2、如图,利用尺规作图在直线L上求作一点P,使PA=PB.
L
A
B
实际问题
数学化
实际问题2
p
PA=PB
第十九页,共24页。
1、已知:在ΔABC中,ON是AB的垂直平分线 OA=OC。求证:点O在BC的垂直平分线上。
A
B
C
O
N
(四)巩固达标,学以致用
2、已知:如图,在等腰三角形ABC中,腰AB的垂直平 线MN交AC于点 D,BC=8厘米, ΔBDC的周长20厘米.
求:AB的长.
3、已知:如图,D是BC延长线上的一点,BD=BC+AC.
求证:点C在AD的垂直平分线上.
A
D
M
A
B
C
D
8
第二十页,共24页。
在公路L的同侧,有二职中和周嘉小学A、B,镇政府计划在公路边上修建一栋图书馆,使得两个学校的师生都没意见,问图书馆的位置应选在何处?
A
B
L
第二十一页,共24页。
二、逆定理:到线段两个端点距离相等的点,在这条
线段的垂直平分线上。
一、性质定理:线段垂直平分线上的点到这条线段两个端
点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是到线段两上端点距离相等的所有点的集合
(五)学习小结,知识内化
第二十二页,共24页。
(六)分层作业、能力升华
必做题 学案 1、2、3题
选做题 在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
链接中考(2022 烟台)等腰△ABC中,AB=AC,A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于()A.80° B.70° C.60°D.50°
第二十三页,共24页。
1、线段的垂直平分线的性质:
线段垂直平分线上的点到线段两端点距离相等 即: ∵ MN垂直平分线段AB ∴ AP=BP AQ=BQ AR=BR
2、判定定理:到线段两端距离相等
的点在线段的垂直平分线上。
M
N
(七)版书设计
第二十四页,共24页。
