初中数学人教版八年级上册12.3 角的平分线的性质说课课件 28张PPT
文档属性
| 名称 | 初中数学人教版八年级上册12.3 角的平分线的性质说课课件 28张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
说教学过程
说教学方法
说 教 材
学法
教法
发现探究 呈现任务
自主学习 探究新知
交流评价 分享成功
学习致用 课后延伸
评价反思 课后巩固
教学背景
教学目标
教学重难点
知识目标
能力目标
情感目标
第一部分 说教材
2
教学目标
通过让学生动手操作、合作交流、自主探究等过程,培养学生用数学知识解决问题的能力.
培养学生探究问题的兴趣,增强解决问题的信心,激发学生应用数学的热情.
掌握用尺规作已知角的平分线的方法,角平分线的性质并能初步运用.
第一部分 说教材
教 学 背 景
1
2
3
教 学 目 标
教 学 重 难 点
第一部分 说教材
重 点
难 点
3
教学重难点
(1)对角平分线性质定理中点到角两边的距离的正确理解;
(2)对于性质定理的运用(学生习惯利用三角形全等的方法)
掌握角平分线的尺规作图,理解角的平分线的性质并能初步运用
从生活中的所见所闻现象导入
让学生自
己观察讨
论
验证推论
的正确性
主要通过 的方法开展教学
教法
第二部分 说教学方法
任务驱动
发现
问题
思考
问题
解决
问题
自主探究法、合作交流法、成果展示法
学法
第二部分 说教学方法
4
第一环节:发现探究 呈现任务
1
2
3
第二环节:自主学习 探究新知
第三环节:交流评价 分享成功
第四环节:学以致用 课后延伸
第三部分 说教学过程
5
第五环节:评价反思 课后巩固
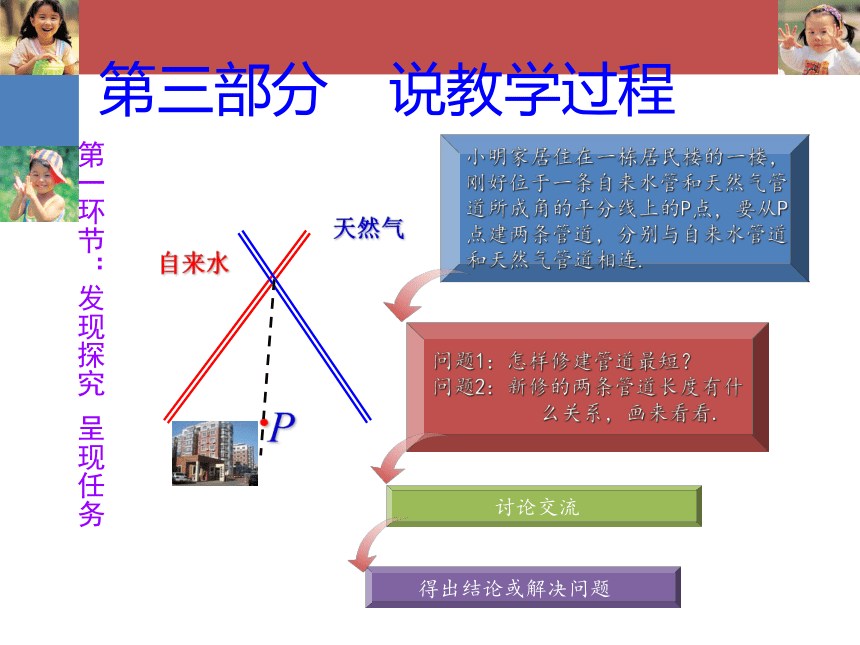
问题1:怎样修建管道最短?
问题2:新修的两条管道长度有什
么关系,画来看看.
小明家居住在一栋居民楼的一楼,刚好位于一条自来水管和天然气管道所成角的平分线上的P点,要从P点建两条管道,分别与自来水管道和天然气管道相连.
讨论交流
得出结论或解决问题
第三部分 说教学过程
第一环节:发现探究 呈现任务
.
P
自来水
天然气
任 务 二
探究角的平分线的性质
任 务 一
探索作已知角的平分线的方法
第三部分 说教学过程
第二环节:自主学习 探究新知
第三部分 说教学过程
任 务 一:探索作已知角的平分线的方法
观察生活中的实例
从生活实例中得出数学原理
A
任务
B
任务
得到角的平分线的作法
C
任务
验证角的平分线的作法
D
任务
第三部分 说教学过程
工人师傅常用如图所示的简易平分角的仪器来画角的平分线:
A
任务
观察生活中的实例
A
任务
·
·
·
·
D
B
A
C
将角的顶点放在A处,AB和AD沿角的两边放下
过AC画一条射线AE,AE即为∠BAD的平分线.
E
第三部分 说教学过程
从生活实例中得出数学原理
B
任务
把简易平分角的仪器放在角的两边
·
·
·
·
A
B
C
D
平分角的仪器两边相等,从几何作图角度怎么画?BC=DC,从几何作图角度怎么画?
第三部分 说教学过程
(2)分别以M,N为圆心.大于MN一半的长为半径作弧.两弧在∠AOB的内部交于C.
(3)作射线OC,则射线OC即为所求
A
O
B
M
N
C
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
得到角的平分线的作法
C
任务
已知:OM=ON,MC=NC.
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌△ONC
(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
A
B
M
N
C
O
验证角的平分线的作法
D
任务
第三部分 说教学过程
求证:OC平分∠AOB.
O
任 务 二
探究角的平分线的性质
小组合作
大胆猜想
探究真理 小心求证
学生分组
自主尝试
采用分层教学法让学生动手操作,让操作比较好的同学指导其他学生,让各个层次的学生都参与。
重点
第三部分 说教学过程
第三部分 说教学过程
用纸剪一个角
问题1:第一次的折痕和角有什么关系?为什么?
把纸片对折,使角
的两边叠合在一起
把对折后的纸片继续折一次,
折出一个直三角形(使第一次
的折痕为斜边)
展开,观察两次折叠形成的三条折痕:
自主尝试
问题2:第二次折叠形成的两条折痕与角的两边有何关 系,它们的长度有何关系?
第三部分 说教学过程
如图:按照折纸的顺序画出角及折纸形成的三条折痕.让学生分组讨论、交流,并用文字语言阐述得到的性质.(角的平分线上的点到角两边的距离相等)
大胆猜想
第三部分 说教学过程
判断正误:
A
O
B
P
E
F
图2
A
图3
O
B
P
E
(3)如图3,在∠AOB的平分线OP上任取一点P,若P到OA的距离为3cm,则P到OB的距离边为3cm.
小心求证
(2)如图2,P是∠AOB的平分线OP上的一点,E、F分别在OA、OB上,则PE=PF.
(1)如图1,P在射线OP上,PE⊥OA,PF⊥OB,则PE=PF.
√
×
×
A
O
B
P
E
F
图1
F
第三部分 说教学过程
第三环节:交流评价 分享成功
让学生运用本节课所学的知识回答课前引例中的问题:
问题:引例中两条管道的长度有什么关系?理由是什么?
.
P
自来水
天然气
1.已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
即点P到边AB、BC、CA的距离相等
A
B
C
P
M
N
D
E
F
第三部分 说教学过程
第四环节:学以致用 课后延伸
[例题讲解]
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,
垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
第三部分 说教学过程
第四环节:学以致用 课后延伸
例1 如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:EB=FC.
A
F
C
D
B
E
[例题讲解]
变形题1:
如图,△ABC中,AD是∠BAC的平分线, ∠C=90°, DE⊥AB于E,F 在AC上,且BD=DF,求证:CF=EB.
变形题2:
如图,△ABC中, AD是∠BAC的平分线, ∠C=90°,DE⊥AB于E,BC=8,BD=5,求DE.
A
F
C
D
B
E
A
C
D
B
E
第四环节:学以致用 课后延伸
第三部分 说教学过程
1)评价反思
a.这节课你有哪些收获,还有什么困惑?
b.通过本节课你了解了哪些思考问题的方法?
c.完成课内反馈练习.
2)课后巩固
必做题:学案第1、2、3题
选做题:学案第6题
第五环节:评价反思 课后巩固
第三部分 说教学过程
2)布置作业作业(必做题)
(1)用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB,为什么?
(2)△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF ⊥ AC,垂足分别为E,F.求证:EB=FC.
(3)如图,CD ⊥ AB,BE ⊥ AC,垂足分别为DE,BE,CD相交于点O,OB=OC.求证:∠1= ∠2
A
F
C
D
B
E
2).布置作业(选做题)
(4)如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF.EF与AD交于G.AD与EF垂直吗?证明你的结论.
A
F
C
D
B
E
G
本节课将信息技术与教学进行有机结合,充分调动学生的自主探究与合作交流,教师注意适时的点拔引导,学生的主人地位和教师的主导作用得以充分体现,切实能够达到发展思维、提升能力的根本目的,能够较好地实现教学目标,也使课标理念能够更好地得到落实.
课后小结
谢谢大家!
说教学过程
说教学方法
说 教 材
学法
教法
发现探究 呈现任务
自主学习 探究新知
交流评价 分享成功
学习致用 课后延伸
评价反思 课后巩固
教学背景
教学目标
教学重难点
知识目标
能力目标
情感目标
第一部分 说教材
2
教学目标
通过让学生动手操作、合作交流、自主探究等过程,培养学生用数学知识解决问题的能力.
培养学生探究问题的兴趣,增强解决问题的信心,激发学生应用数学的热情.
掌握用尺规作已知角的平分线的方法,角平分线的性质并能初步运用.
第一部分 说教材
教 学 背 景
1
2
3
教 学 目 标
教 学 重 难 点
第一部分 说教材
重 点
难 点
3
教学重难点
(1)对角平分线性质定理中点到角两边的距离的正确理解;
(2)对于性质定理的运用(学生习惯利用三角形全等的方法)
掌握角平分线的尺规作图,理解角的平分线的性质并能初步运用
从生活中的所见所闻现象导入
让学生自
己观察讨
论
验证推论
的正确性
主要通过 的方法开展教学
教法
第二部分 说教学方法
任务驱动
发现
问题
思考
问题
解决
问题
自主探究法、合作交流法、成果展示法
学法
第二部分 说教学方法
4
第一环节:发现探究 呈现任务
1
2
3
第二环节:自主学习 探究新知
第三环节:交流评价 分享成功
第四环节:学以致用 课后延伸
第三部分 说教学过程
5
第五环节:评价反思 课后巩固
问题1:怎样修建管道最短?
问题2:新修的两条管道长度有什
么关系,画来看看.
小明家居住在一栋居民楼的一楼,刚好位于一条自来水管和天然气管道所成角的平分线上的P点,要从P点建两条管道,分别与自来水管道和天然气管道相连.
讨论交流
得出结论或解决问题
第三部分 说教学过程
第一环节:发现探究 呈现任务
.
P
自来水
天然气
任 务 二
探究角的平分线的性质
任 务 一
探索作已知角的平分线的方法
第三部分 说教学过程
第二环节:自主学习 探究新知
第三部分 说教学过程
任 务 一:探索作已知角的平分线的方法
观察生活中的实例
从生活实例中得出数学原理
A
任务
B
任务
得到角的平分线的作法
C
任务
验证角的平分线的作法
D
任务
第三部分 说教学过程
工人师傅常用如图所示的简易平分角的仪器来画角的平分线:
A
任务
观察生活中的实例
A
任务
·
·
·
·
D
B
A
C
将角的顶点放在A处,AB和AD沿角的两边放下
过AC画一条射线AE,AE即为∠BAD的平分线.
E
第三部分 说教学过程
从生活实例中得出数学原理
B
任务
把简易平分角的仪器放在角的两边
·
·
·
·
A
B
C
D
平分角的仪器两边相等,从几何作图角度怎么画?BC=DC,从几何作图角度怎么画?
第三部分 说教学过程
(2)分别以M,N为圆心.大于MN一半的长为半径作弧.两弧在∠AOB的内部交于C.
(3)作射线OC,则射线OC即为所求
A
O
B
M
N
C
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
得到角的平分线的作法
C
任务
已知:OM=ON,MC=NC.
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌△ONC
(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
A
B
M
N
C
O
验证角的平分线的作法
D
任务
第三部分 说教学过程
求证:OC平分∠AOB.
O
任 务 二
探究角的平分线的性质
小组合作
大胆猜想
探究真理 小心求证
学生分组
自主尝试
采用分层教学法让学生动手操作,让操作比较好的同学指导其他学生,让各个层次的学生都参与。
重点
第三部分 说教学过程
第三部分 说教学过程
用纸剪一个角
问题1:第一次的折痕和角有什么关系?为什么?
把纸片对折,使角
的两边叠合在一起
把对折后的纸片继续折一次,
折出一个直三角形(使第一次
的折痕为斜边)
展开,观察两次折叠形成的三条折痕:
自主尝试
问题2:第二次折叠形成的两条折痕与角的两边有何关 系,它们的长度有何关系?
第三部分 说教学过程
如图:按照折纸的顺序画出角及折纸形成的三条折痕.让学生分组讨论、交流,并用文字语言阐述得到的性质.(角的平分线上的点到角两边的距离相等)
大胆猜想
第三部分 说教学过程
判断正误:
A
O
B
P
E
F
图2
A
图3
O
B
P
E
(3)如图3,在∠AOB的平分线OP上任取一点P,若P到OA的距离为3cm,则P到OB的距离边为3cm.
小心求证
(2)如图2,P是∠AOB的平分线OP上的一点,E、F分别在OA、OB上,则PE=PF.
(1)如图1,P在射线OP上,PE⊥OA,PF⊥OB,则PE=PF.
√
×
×
A
O
B
P
E
F
图1
F
第三部分 说教学过程
第三环节:交流评价 分享成功
让学生运用本节课所学的知识回答课前引例中的问题:
问题:引例中两条管道的长度有什么关系?理由是什么?
.
P
自来水
天然气
1.已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
即点P到边AB、BC、CA的距离相等
A
B
C
P
M
N
D
E
F
第三部分 说教学过程
第四环节:学以致用 课后延伸
[例题讲解]
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,
垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
第三部分 说教学过程
第四环节:学以致用 课后延伸
例1 如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:EB=FC.
A
F
C
D
B
E
[例题讲解]
变形题1:
如图,△ABC中,AD是∠BAC的平分线, ∠C=90°, DE⊥AB于E,F 在AC上,且BD=DF,求证:CF=EB.
变形题2:
如图,△ABC中, AD是∠BAC的平分线, ∠C=90°,DE⊥AB于E,BC=8,BD=5,求DE.
A
F
C
D
B
E
A
C
D
B
E
第四环节:学以致用 课后延伸
第三部分 说教学过程
1)评价反思
a.这节课你有哪些收获,还有什么困惑?
b.通过本节课你了解了哪些思考问题的方法?
c.完成课内反馈练习.
2)课后巩固
必做题:学案第1、2、3题
选做题:学案第6题
第五环节:评价反思 课后巩固
第三部分 说教学过程
2)布置作业作业(必做题)
(1)用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB,为什么?
(2)△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF ⊥ AC,垂足分别为E,F.求证:EB=FC.
(3)如图,CD ⊥ AB,BE ⊥ AC,垂足分别为DE,BE,CD相交于点O,OB=OC.求证:∠1= ∠2
A
F
C
D
B
E
2).布置作业(选做题)
(4)如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF.EF与AD交于G.AD与EF垂直吗?证明你的结论.
A
F
C
D
B
E
G
本节课将信息技术与教学进行有机结合,充分调动学生的自主探究与合作交流,教师注意适时的点拔引导,学生的主人地位和教师的主导作用得以充分体现,切实能够达到发展思维、提升能力的根本目的,能够较好地实现教学目标,也使课标理念能够更好地得到落实.
课后小结
谢谢大家!
