2023-2024学年江苏省苏州市苏州工业园区星湾学校九年级(上)期中数学试卷(图片版,含解析)
文档属性
| 名称 | 2023-2024学年江苏省苏州市苏州工业园区星湾学校九年级(上)期中数学试卷(图片版,含解析) |  | |
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 23:24:30 | ||
图片预览



文档简介
江苏省苏州市苏州工业园区星湾学校
2023-2024 学年九年级上学期期中数学试题
一、单选题
1.下列方程是一元二次方程的是( )
A. x2
1
2xy 5 B 2. x 2
x
C. x2 y2 6 D. x2 5
2.抛物线 y 2x2 的对称轴是直线( )
A. y 0 B. y 1 C. x 0 D. x 2
3.用配方法解方程 x2 6x 4 0,原方程应变为( )
A. (x 3)2 13 B. (x 3)2 5 C. (x 3)2 13 D. (x 3)2 5
4.如图,点 A,B,C,D在 O上, AOC 142 ,点 B是 AC的中点,则 D的度数
是( )
A.70 B.55 C. 35.5 D.35
5.由二次函数 y=(2 x﹣3)2 1,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线 x=﹣3
C.其最小值为 1 D.当 x<3 时,y随 x的增大而增大
6.如图所示的网格由边长相同的小正方形组成,点 A、B、C、D、E、F 在小正方形的
顶点上,则△ABC 的外心是( )
A.点 D B.点 E C.点 F D.点 G
试卷第 1页,共 29页
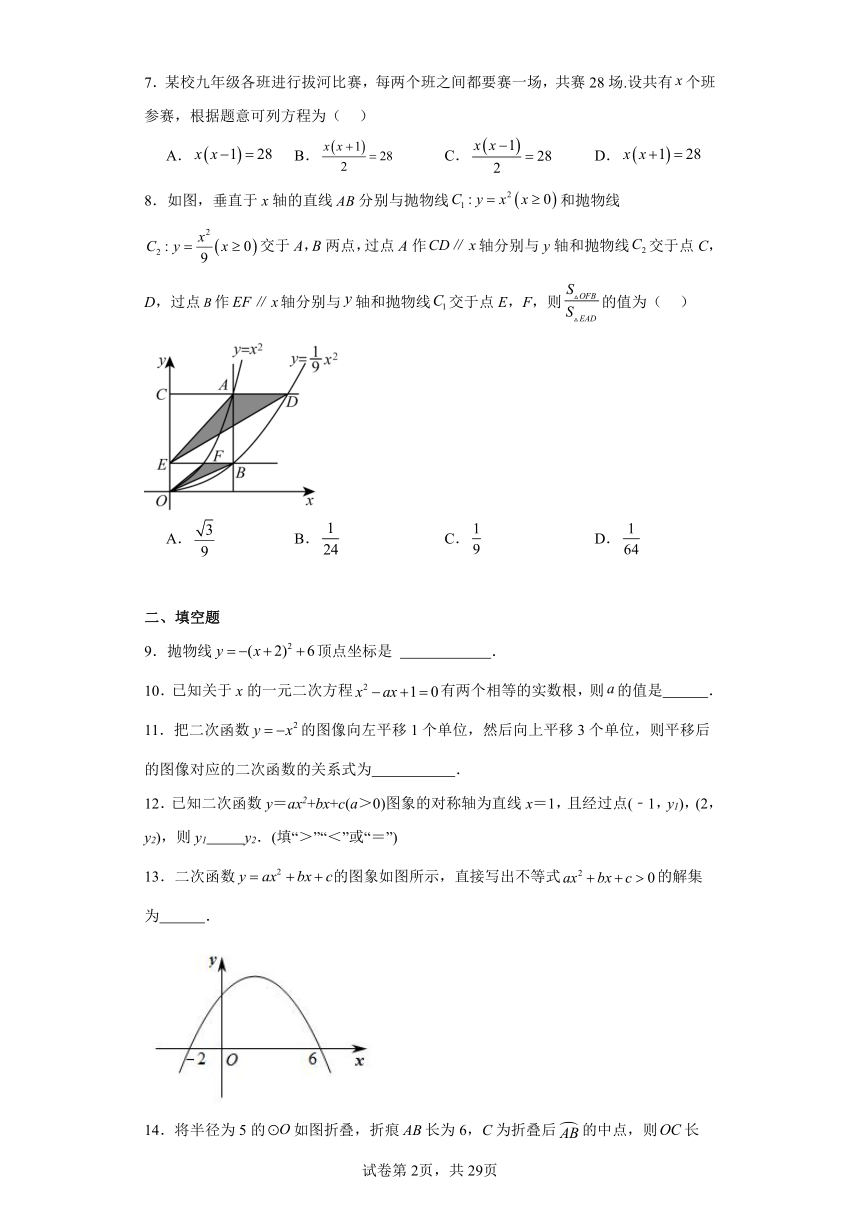
7.某校九年级各班进行拔河比赛,每两个班之间都要赛一场,共赛 28 场.设共有 x个班
参赛,根据题意可列方程为( )
x x 1 28 xA B x 1 x x 1 . . 28 C. 28 D. x x 1 28
2 2
8 x AB C : y x2.如图,垂直于 轴的直线 分别与抛物线 1 x 0 和抛物线
2
C2 : y
x
x 0 交于 A,B两点,过点 A作CD∥ x轴分别与 y轴和抛物线C2 交于点 C,9
S
D,过点 B EF x OFB作 ∥ 轴分别与 y轴和抛物线C1交于点 E,F,则 S 的值为( ) EAD
3 1 1 1A. B. C. D.
9 24 9 64
二、填空题
9.抛物线 y (x 2)2 6顶点坐标是 .
10.已知关于 x的一元二次方程 x2 ax 1 0有两个相等的实数根,则 a的值是 .
11.把二次函数 y x2 的图像向左平移 1 个单位,然后向上平移 3 个单位,则平移后
的图像对应的二次函数的关系式为 .
12.已知二次函数 y=ax2+bx+c(a>0)图象的对称轴为直线 x=1,且经过点(﹣1,y1),(2,
y2),则 y1 y2.(填“>”“<”或“=”)
13.二次函数 y ax2 bx c的图象如图所示,直接写出不等式 ax2 bx c 0的解集
为 .
14.将半径为 5 的 O如图折叠,折痕 AB长为 6,C为折叠后 AB的中点,则OC长
试卷第 2页,共 29页
为 .
15.对于两个不相等的实数 a、b,我们规定符号Max{a,b}表示 a、b中的较大值,如:
Max{1,3} 3,按照这个规定,方程Max{1,x} x 2 6 的解为 .
16.如图,正方形OABC的边长为 4,OA与 x轴负半轴的夹角为15 ,点 B在抛物线
y ax 2 a 0 的图象上,则 a的值为 .
三、计算题
17.解方程:
(1) x 5 2 16;
(2) 2x2 1 4x.
(3)5x x 1 2 x 1
(4) 2x2 x 1 0.
四、作图题
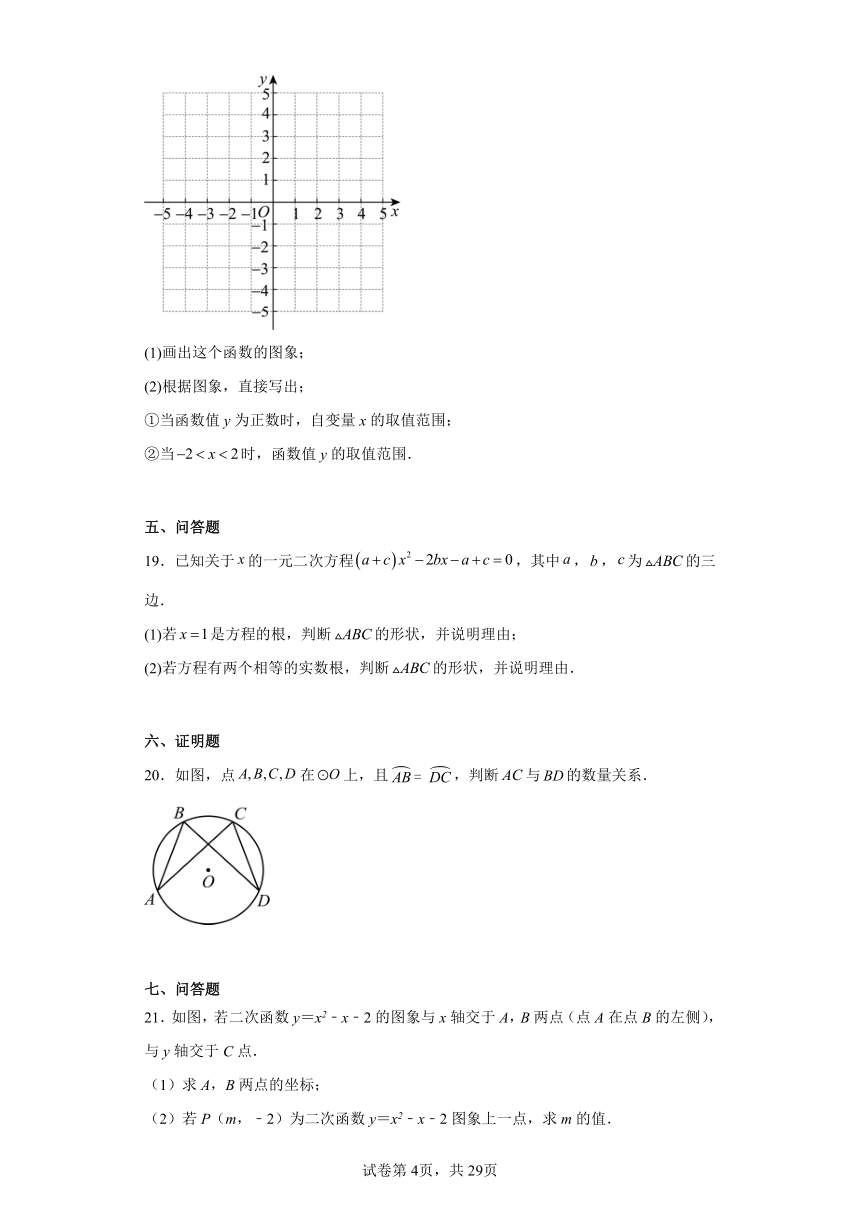
18.已知二次函数 y x2 2x 3.
试卷第 3页,共 29页
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值 y为正数时,自变量 x的取值范围;
②当 2 x 2时,函数值 y的取值范围.
五、问答题
19 2.已知关于 x的一元二次方程 a c x 2bx a c 0,其中 a,b,c为 ABC的三
边.
(1)若 x 1是方程的根,判断 ABC的形状,并说明理由;
(2)若方程有两个相等的实数根,判断 ABC的形状,并说明理由.
六、证明题
20.如图,点 A,B,C,D在 O上,且 AB = D C,判断 AC与 BD的数量关系.
七、问答题
21.如图,若二次函数 y=x2﹣x﹣2 的图象与 x轴交于 A,B两点(点 A在点 B的左侧),
与 y轴交于 C点.
(1)求 A,B两点的坐标;
(2)若 P(m,﹣2)为二次函数 y=x2﹣x﹣2 图象上一点,求 m的值.
试卷第 4页,共 29页
八、应用题
22.某品牌服装平均每天可以售出 10 件,每件盈利 40 元.受新冠肺炎疫情影响,商场
决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:每件服装每降价
1 元,平均每天就可以多售出 2 件,如果需要盈利 700 元,那么每件降价多少元
九、证明题
23.如图,⊙O的直径 AB为 6cm,∠ACB的平分线交⊙O于点 D.
(1)判断 ADB的形状,并证明;
(2)求 BD的长.
十、应用题
24.某农场要建一个矩形动物场,场地的一边靠墙(墙 AB长度小于 10 米),另外三边
用木栏围成,木栏总长 20 米,设动物场CD边的长为 xm ,矩形面积为 ym2 .
(1)矩形面积 y ______(用含 x的代数式表示);
(2)当矩形动物场面积为48m2 时,求CD边的长;
(3)能否围成面积为52m2 矩形动物场 说明理由.
试卷第 5页,共 29页
十一、计算题
25.如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,OA 2m ,从A 处
向外喷出的水流在各个方向上沿形状相同的抛物线路径落下.王丽芳同学根据题意在图
中建立如图所示的坐标系,水流喷出的高度 y m 与水平距离 x m 之间的关系式是
y ax 2 bx c x 0 1,已知水流的最高点到OA的水平距离是 m ,最高点离水面是
2
9 m .
4
求二次函数表达式;
(1)若不计其他因素,水池的半径至少为多少米,才能使喷出的水流不至于落在池外
十二、问答题
26.如图,在平面直角坐标系 xOy中,直线 y x t与坐标轴交于A 、C两点,经过A 、
C两点的抛物线 y ax2 bx 6与 x轴的另一交点 B的坐标为 2,0 ,连接 BC.
(1)填空: t ______,a ______,b ______;
(2)若点Q在直线 AC下方的抛物线上一动点,连接 AQ、CQ,当 S△AQC 12 ,求点Q的
坐标;
(3)若点Q在直线 AC下方的抛物线上一动点,当CA恰好平分 BCQ时,求点Q横坐标.
十三、计算题
27.定义:若一个函数图像中存在横、纵坐标相等的点,则称该点为这个函数图像的“等
值点”,例如:点 1,1 是函数 y 2x 1的图像的“等值点”.
试卷第 6页,共 29页
(1)分别判断函数 y 2x 1,y x2 x 2的图像上是否存在“等值点” 如果存在,求出“等
值点”的坐标;如果不存在,请说明理由;
9
(2)设函数 y x 0 , y x b x 0 的图像的“等值点”分别为点 A、B,过点 B作
x
BC x轴,垂足为C,当 ABC面积为 3 时,求b的值;
(3) 2若函数 y x 4 x m 的图像记为W1 ,将其沿直线 x m翻折后的图像记为W2 ,当
W,与W2 组合成的图像上恰有两个“等值点”时,请求出m的取值范围.
试卷第 7页,共 29页
江苏省苏州市苏州工业园区星湾学校
2023-2024 学年九年级上学期期中数学试题
一、单选题
1.下列方程是一元二次方程的是( )
A. x2
1
2xy 5 B x2. 2
x
C. x2 y2 6 D. x2 5
【答案】D
【分析】直接根据一元二次方程的定义逐项判断即可.
【详解】解:A、 x2 2xy 5 中含有两个未知数,不是一元二次方程,故本选项不符合
题意;
B x2
1
、 2是分式方程,不是一元二次方程,故本选项不符合题意;
x
C、 x2 y2 6中含有两个未知数,不是一元二次方程,故本选项不符合题意;
D、 x2 5,是一元二次方程,故本选项符合题意;
故选:D.
【点睛】本题考查了一元二次方程的定义,只含有一个未知数,并且所含未知数的项的
最高次数是 2 的整式方程叫一元二次方程,熟练掌握此定义是解题的关键.
2.抛物线 y 2x2 的对称轴是直线( )
A. y 0 B. y 1 C. x 0 D. x 2
【答案】C
【分析】根据抛物线解析式,可直接求出对称轴.
【详解】解: 抛物线解析式为 y 2x2 ,
对称轴为 x 0.
故选:C.
2
【点睛】本题考查二次函数的性质,解题的关键是记住二次函数 y = ax (a 0)的对称
轴是直线 x 0.
3.用配方法解方程 x2 6x 4 0,原方程应变为( )
A. (x 3)2 13 B. (x 3)2 5 C. (x 3)2 13 D. (x 3)2 5
【答案】D
【分析】先将常数项移到右边,两边再同时加上一次项系数一半的平方进行配方即可得
试卷第 8页,共 29页
到答案.
【详解】对 x2 6x 4 0进行配方:
移项,得: x2 6x 4,
6
2
两边同时加上一次项系数一半的平方,即 9,得:
2
x2 6x 9 4 9 ,
2
整理,得: x 3 5,
故选:D.
【点睛】本题考查一元二次方程的配方,熟练掌握配方的过程是本题的解题关键.
4.如图,点 A,B,C,D在 O上, AOC 142 ,点 B是 AC的中点,则 D的度数
是( )
A.70 B.55 C. 35.5 D.35
【答案】C
【分析】本题主要考查的是圆心角、弧、弦的关系定理、圆周角定理.根据圆心角、弧、
1
弦的关系定理得到 AOB AOC2 ,再根据圆周角定理解答.
【详解】解:连接OB,如图所示:
∵点 B是 AC的中点,
∴ AOB
1
AOC 71 ,
2
试卷第 9页,共 29页
1
由圆周角定理得, D AOB 35.5 ,故 C 正确.
2
故选:C.
5.由二次函数 y=(2 x﹣3)2 1,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线 x=﹣3
C.其最小值为 1 D.当 x<3 时,y随 x的增大而增大
【答案】C
【分析】由解析式可知 a>0,对称轴为 x=3,最小值为 0,在对称轴的左侧 y随 x的增
大而减小,可得出答案.
【详解】由二次函数 y=(2 x﹣3)2 1,可知:
A:∵a>0,其图象的开口向上,故此选项错误;
B.∵其图象的对称轴为直线 x=3,故此选项错误;
C.其最小值为 1,故此选项正确;
D.当 x<3 时,y随 x的增大而减小,故此选项错误.
故选:C.
【点睛】本题主要考查二次函数的性质,掌握二次函数的开口方向、对称轴、顶点坐标、
最大值及对称轴两侧的增减性是解题的关键.属于基础题目.
6.如图所示的网格由边长相同的小正方形组成,点 A、B、C、D、E、F 在小正方形的
顶点上,则△ABC 的外心是( )
A.点 D B.点 E C.点 F D.点 G
【答案】A
【分析】根据三角形三边中垂线相交于一点,这一点叫做它的外心,据此解答即可.
【详解】根据图形可知,直线 DG 是△ABC 的 BC 边上的中垂线,点 D 在△ABC 的 AB
边上的中垂线上,
∴点 D 是△ABC 外心.
故选:A.
【点睛】本题主要考查了三角形的外心的定义,注意:三角形三边中垂线相交于一点,
试卷第 10页,共 29页
这一点是此三角形的外心.
7.某校九年级各班进行拔河比赛,每两个班之间都要赛一场,共赛 28 场.设共有 x个班
参赛,根据题意可列方程为( )
A. x x 1 28 x x 1B x x 1C . 28 . 28 D. x x 1 28
2 2
【答案】C
【分析】根据互动问题直接列式即可得到答案;
【详解】解:由题意可得,
x x 1
28,
2
故选:C;
【点睛】本题考查一元二次方程解应用题,解题的关键是互动问题注意重复问题.
8 2.如图,垂直于 x轴的直线 AB分别与抛物线C1 : y x x 0 和抛物线
2
C2 : y
x
x 0 交于 A,B两点,过点 A作CD∥ x轴分别与 y轴和抛物线C2 交于点 C,9
S
D,过点 B作 EF OFB∥ x轴分别与 y轴和抛物线C1交于点 E,F,则 S 的值为( ) EAD
3 1 1 1A. B. C. D.
9 24 9 64
【答案】B
【分析】此题重点考查学生对二次函数的图象和性质的应用能力.根据二次函数的图象
和性质结合三角形面积公式求解.
a2
【详解】解:设点 A,B横坐标为 a,则点A 纵坐标为 a 2 ,点 B的纵坐标为 ,
9
BE∥ x轴,
F a
2
∴点 纵坐标为 ,
9
∵点 F 是抛物线 y = x2上的点,
1
∴点 F 横坐标为 x y a,
3
CD x轴,
试卷第 11页,共 29页
∴点D纵坐标为 a 2 ,
x2
∵点D是抛物线 y 上的点,
9
∴点D横坐标为 x 9y 3a,
AD 2a,BF 2 a CE 8 a2 OE 1 , , a2 ,
3 9 9
1 BF OE 1S OFB 2 27 1 1 ,S EAD AD CE 8 24
2 9
故选:B.
二、填空题
9.抛物线 y (x 2)2 6顶点坐标是 .
【答案】 ( 2,6)
【分析】本题考查了求二次函数的性质,根据抛物线的顶点式直接求得顶点坐标.
【详解】抛物线 y (x 2)2 6的顶点坐标是 ( 2,6) ,
故答案为: ( 2,6) .
10.已知关于 x的一元二次方程 x2 ax 1 0有两个相等的实数根,则 a的值是 .
【答案】 2
【分析】本题主要考查根的判别式,根据方程有两个相等的实数根时 b2 4ac 0列
出方程,解之可得答案.
【详解】解:∵关于 x的一元二次方程 x2 ax 1 0有两个相等的实数根,
2
∴ a 4 1 1 0 ,即 a 2 4 0
解得, a 2,
故答案为: 2.
11.把二次函数 y x2 的图像向左平移 1 个单位,然后向上平移 3 个单位,则平移后
的图像对应的二次函数的关系式为 .
2
【答案】 y x 1 3
【分析】直接运用平移规律“左加右减,上加下减”解答.
【详解】解:把二次函数 y x2 的图像向左平移 1 个单位,然后向上平移 3 个单位得
2
到的二次函数的关系式为 y x 1 3 ,
试卷第 12页,共 29页
故答案为: y x 1 2 3 .
【点睛】本题主要考查了二次函数图象的平移,要求熟练掌握平移的规律:左加右减,
上加下减.
12.已知二次函数 y=ax2+bx+c(a>0)图象的对称轴为直线 x=1,且经过点(﹣1,y1),(2,
y2),则 y1 y2.(填“>”“<”或“=”)
【答案】>
【分析】根据二次函数 y=ax2+bx+c(a>0)图象的对称轴为直线 x=1,且经过点(﹣1,y1),
(2,y2)和二次函数的性质可以判断 y1 和 y2的大小关系.
【详解】解:∵二次函数 y=ax2+bx+c(a>0)图象的对称轴为直线 x=1,
∴当 x>1 时,y随 x的增大而增大,当 x<1 时,y随 x的增大而减小,
∵该函数经过点(﹣1,y1),(2,y2),|﹣1﹣1|=2,|2﹣1|=1,
∴y1>y2,
故答案为:>.
【点睛】本题考查了二次函数的增减性问题,掌握二次函数的性质是解题的关键.
13.二次函数 y ax2 bx c的图象如图所示,直接写出不等式 ax2 bx c 0的解集
为 .
【答案】 2 x 6
【分析】根据二次函数图像找到 x轴上方图像 x取值范围即可得到答案.
【详解】解:由二次函数图像可得,
当 2 x 6 时, y 0 ,
故答案为: 2 x 6 .
【点睛】本题考查根据二次函数图像解一元二次不等式,解题的关键是熟练掌握二次函
数与一元二次不等式的关系.
14.将半径为 5 的 O如图折叠,折痕 AB长为 6,C为折叠后 AB的中点,则OC长
为 .
试卷第 13页,共 29页
【答案】3
【分析】本题考查了垂径定理,圆心角、弧、弦的关系和勾股定理.延长OC交 O于
D点,交 AB于 E点,连接OA、OB、AC、BC ,如图根据圆心角、弧、弦的关系由 AC B C
得到CA CB,则可判断OC垂直平分 AB,则 AE BE 3,再利用勾股定理计算出
OE 4 ,所以DE 1,然后利用 C点和 D点关于 AB对称得到CE 1,最后计算OE CE
即可.
【详解】解:延长OC交 O于 D点,交 AB于 E点,连接OA、OB、AC、BC,如图,
∵C为折叠后 AB的中点,
∴ AC B C,
∴CA CB,
∵OA OB,
∴OC垂直平分 AB,
1
∴AE BE AB 3,
2
在Rt△AOE中,OE OA2 AE2 52 32 4,
∴DE OD OE 5 4 1,
∵ ADB沿 AB折叠得到 A CB,CD垂直 AB,
∴C点和 D点关于 AB对称,
∴CE=DE=1,
∴OC OE CE 4 1 3.
故答案为:3.
15.对于两个不相等的实数 a、b,我们规定符号Max{a,b}表示 a、b中的较大值,如:
Max{1,3} 3,按照这个规定,方程Max{1,x} x 2 6 的解为 .
【答案】 x 3或 x 7
试卷第 14页,共 29页
【分析】分类讨论 x的范围,利用题中的新定义,列出方程,解方程即可.
【详解】解:当 x 1时,方程为: x2 6 x
即 x2 x 6 0,
解得: x1 2 (舍去), x2 3;
∴此时 x 3,
当 x 1时,方程为: x2 6 1,
解得: x1 7 (舍去), x2 7 ,
∴ x 7 ;
故答案为: x 3或 x 7 .
【点睛】本题主要考查了解一元二次方程,新定义实数运算,解题的关键是理解题意,
列出方程求解.
16.如图,正方形OABC的边长为 4,OA与 x轴负半轴的夹角为15 ,点 B在抛物线
y ax 2 a 0 的图象上,则 a的值为 .
2
【答案】
12
【分析】本题主要考查了正方形的性质、直角三角形的性质以及用待定系数法确定函数
解析式的方法,连接OB,过 B作 BD x轴于 D,若OA与 x轴负半轴的夹角为15 ,那
么 BOD 30 ;在正方形OABC中,已知了边长,易求得对角线OB的长,进而可在
Rt△OBD中求得 BD、OD的值,也就得到了 B点的坐标,然后将其代入抛物线的解析
式中,即可求得待定系数 a的值.
【详解】解:如图,连接OB,过 B作 BD x轴于 D;
则 BOA 45 , BOD 30 ;
试卷第 15页,共 29页
已知正方形的边长为 4,则OB 4 2 ;
Rt△OBD中,OB 4 2 , BOD 30 ,
BD 1则 OB 2 2,OD OB2 BD2 2 6 ;
2
故 B 2 6, 2 2 ,
2
代入抛物线的解析式中,得: 2 6 a 2 2 ,
2
解得 a ,
12
2
故答案为: .
12
三、计算题
17.解方程:
(1) x 5 2 16;
(2) 2x2 1 4x.
(3)5x x 1 2 x 1
(4) 2x2 x 1 0.
【答案】(1) x 9, x2 1
(2) x1 1
6
, x2 1
6
2 2
(3) x1 1, x
2
2 5
1
(4) x1 1, x2 2
【分析】本题主要考查解一元二次方程的能力:
(1)利用直接开平方法求解即可;
(2)利用配方法求解即可;
(3)先移项,再将左边利用提公因式法因式分解,继而可得两个关于 x的一元一次方
程,分别求解即可得出答案;
(4)利用公式法求解可得方程的解.
2
【详解】(1)∵ x 5 16,
∴ x 5 4,
∴ x 9 , x2 1;
试卷第 16页,共 29页
(2) 2x2 1 4x,
2x2 4x 1 0,
x2 1 2x 0,
2
x2 2x 1 ,
2
x2 2x 1 3 ,
2
x 1 2 3 ,
2
x 1 6 ,
2
6 6
∴ x1 1 , x2 1 ;2 2
(3)5x x 1 2 x 1 ,
5x x 1 2 x 1 0,
(x 1)(5x 2) 0
x 1 0或5x 2 0,
2
∴ x1 1, x2 5 ;
(4) 2x2 x 1 0,
这里 a 2,b = -1,c 1,
△ 1 2 4 2 1 9 0 ,
b b2 4ac 1 9x 1 3则 ,
2a 4 4
∴ x1 1, x
1
2 .2
【点睛】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方
法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的
方法是解题的关键.
四、作图题
18.已知二次函数 y=﹣x2+2x+3.
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值 y 为正数时,自变量 x 的取值范围;
②当﹣2<x<2 时,函数值 y 的取值范围.
试卷第 17页,共 29页
【答案】(1)见解析;(2)①﹣1<x<3;②﹣5<y<4.
【详解】(1)配方后即可确定顶点坐标及对称轴;
(2)确定顶点坐标及对称轴、与坐标轴的交点坐标即可确定抛物线的解析式;
(3)根据图象利用数形结合的方法确定答案即可;
五、问答题
19 2.已知关于 x的一元二次方程 a c x 2bx a c 0,其中 a,b,c为 ABC的三
边.
(1)若 x 1是方程的根,判断 ABC的形状,并说明理由;
(2)若方程有两个相等的实数根,判断 ABC的形状,并说明理由.
【答案】(1)等腰三角形,理由见解析
(2)直角三角形,理由见解析
【分析】(1)根据方程的解把 x=1 代入方程得到 c﹣b=0,即 c=b,于是由等腰三角形的
判定即可得到 ABC是等腰三角形;
(2)根据根的判别式得出 a,b,c的关系,即可根据勾股定理的逆定理判断△ABC的
形状.
【详解】(1)解:把 x=1 代入方程得,
a c 2b a c 0 ,
化简得 c b,
则该三角形 ABC的形状为等腰三角形.
(2)解:由题意可得方程有两个相等的实数根
2 2
则 a c x 2bx a c 0的判别式:Δ 2b 4 a c a c 0
4b2 4 (c2 a2) 0
试卷第 18页,共 29页
化简可得b2 a2 c2
则该三角形 ABC的形状为直角三角形.
【点睛】本题考查了根的判别式以及一元二次方程、等腰三角形的判定、直角三角形的
判定,掌握一元二次方程根的判别式是解题的关键.
六、证明题
20.如图,点 A,B,C,D在 O上,且 AB = D C,判断 AC与 BD的数量关系.
【答案】 AC BD
【分析】本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦
中有一组量相等,则另外两组量也对应相等.由 AB = D C,可得 AB+ B C = D C + B C,
即 AC B D,因此 AC与 BD相等.
【详解】解: AC BD.理由如下:
∵ AB = D C,
∴ AB+ B C = D C + B C,
即 AC B D,
∴ AC BD.
七、问答题
21.如图,若二次函数 y=x2﹣x﹣2 的图象与 x轴交于 A,B两点(点 A在点 B的左侧),
与 y轴交于 C点.
(1)求 A,B两点的坐标;
(2)若 P(m,﹣2)为二次函数 y=x2﹣x﹣2 图象上一点,求 m的值.
试卷第 19页,共 29页
【答案】(1)A(-1,0),B(2,0);(2)m的值为 0 或 1.
【分析】(1)解方程 x2-x-2=0 可得 A,B两点的坐标;
(2)把 P(m,-2)代入 y=x2-x-2 得 m2-m-2=-2,然后解关于 m的方程即可.
【详解】解:(1)当 y=0 时,x2-x-2=0,解得 x1=-1,x2=2,
∴A(-1,0),B(2,0);
(2)把 P(m,-2)代入 y=x2-x-2 得 m2-m-2=-2,
解得 m1=0,m2=1,
∴m的值为 0 或 1.
【点睛】本题考查了抛物线与 x轴的交点:把求二次函数 y=ax2+bx+c(a,b,c是常数,
a≠0)与 x轴的交点坐标问题转化为解关于 x的一元二次方程.
八、应用题
22.某品牌服装平均每天可以售出 10 件,每件盈利 40 元.受新冠肺炎疫情影响,商场
决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:每件服装每降价
1 元,平均每天就可以多售出 2 件,如果需要盈利 700 元,那么每件降价多少元
【答案】每件降价5元或30元.
【分析】本题考查了一元二次方程的应用.设每件降价 x元,则每件盈利 40 x 元,
平均每天可售出 10 2x 件,利用总利润=每件盈利×平均每天的销售量,即可得出关
于 x的一元二次方程,解之即可得出结论.
【详解】解:设每件降价 x元,则每件盈利 40 x 元,
依题意得: 40 x 10 2x 700,
整理得: x2 35x 150 8,
解得: x1 5, x2 30.
答:每件降价5元或30元.
试卷第 20页,共 29页
九、证明题
23.如图,⊙O的直径 AB为 6cm,∠ACB的平分线交⊙O于点 D.
(1)判断 ADB的形状,并证明;
(2)求 BD的长.
【答案】(1)等腰直角三角形,见解析;(2)3 2
【分析】(1)先根据角平分线定义得∠ACD = ∠DCB,再利用圆周角定理得∠ACD =
∠ABD,∠DCB = ∠DAB,等量代换即可求解,
(2)利用直径和勾股定理即可得出答案.
【详解】(1)△ADB是等腰直角三角形.
证明:∵CD平分∠ACB,
∴ ∠ACD = ∠DCB.
∵ ∠ACD = ∠ABD,∠DCB = ∠DAB,
∴ ∠ABD = ∠DAB.
∴AD=BD.
∵AB是直径,
∴∠ADB=90°
∴△ADB是等腰直角三角形
(2)在 Rt△ADB中, AD2+BD2=AB2,
∴2BD2=AB2,
∴BD= 2 AB= 2 ×6= 3 2 (cm)
2 2
【点睛】此题考查了圆周角定理、等腰直角三角形的判定与性质以及勾股定理等知识,
熟练掌握圆周角定理和等腰直角三角形的判定与性质是解题的关键.
试卷第 21页,共 29页
十、应用题
24.某农场要建一个矩形动物场,场地的一边靠墙(墙 AB长度小于 10 米),另外三边
用木栏围成,木栏总长 20 米,设动物场CD边的长为 xm ,矩形面积为 ym2 .
(1)矩形面积 y ______(用含 x的代数式表示);
(2)当矩形动物场面积为48m2 时,求CD边的长;
(3)能否围成面积为52m2 矩形动物场 说明理由.
【答案】(1) 2x2 20x m2
(2) 6m
(3)不能,理由见解析
【分析】本题考查了列代数式和一元二次方程的应用.
(1)根据矩形的面积=长×宽求解即可;
(2)根据矩形动物场面积为 48m2 ,列一元二次方程,求解即可;
(3)根据矩形动物场面积为52m2 列一元二次方程,求解即可.
【详解】(1)∵动物场CD边的长为 xm ,木栏总长 20 米,则 EF CD xm,
∴DE 20 2x 米,
y CD DE x 20 2x 2x2∴矩形面积为 20x m2 ,
2x2 20x m2故答案为: ;
(2)根据题意,得 2x2 20x 48 ,
解得 x1 4,x2 6,
∵墙 AB长度小于10m,
∴当CD 4m时,DE 20 2 4 12m 10m ,不符合题意;
当CD 6m时,DE 20 2 6 8m 10m ,符合题意;
所以,CD边的长为6m;
(3)不能,理由如下:
试卷第 22页,共 29页
根据题意,得 2x2 20x 52,
整理,得 x2 10x 26 0,
∵ 100 4 1 26 4 0,
∴方程没有实数根,
∴不能围成面积为52m2 矩形动物场.
十一、计算题
25.如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,OA 2m ,从A 处
向外喷出的水流在各个方向上沿形状相同的抛物线路径落下.王丽芳同学根据题意在图
中建立如图所示的坐标系,水流喷出的高度 y m 与水平距离 x m 之间的关系式是
y ax 2 bx c x 0 1,已知水流的最高点到OA的水平距离是 m ,最高点离水面是
2
9 m .
4
求二次函数表达式;
(1)若不计其他因素,水池的半径至少为多少米,才能使喷出的水流不至于落在池外
y x2 1【答案】(1) x
1
2 2
(2)水池的半径至少为 1 米
【分析】本题考查了待定系数法求解析式,二次函数的实际应用.
(1)根据抛物线的顶点式求解即可.
(2)令 y 0 得到 x2
1 x 1 0 求得抛物线与 x轴正半轴的交点坐标,其横坐标就是
2 2
所求.
1 9 1
【详解】(1)∵水流的最高点到OA的水平距离是 m ,最高点离水面是 m,OA m ,
4 16 2
1 9 1
∴抛物线的顶点坐标为 , , A 0, ,
4 16 2
1 2 9
故设抛物线的解析式为 y a x ,
4 16
试卷第 23页,共 29页
1 2
∴ a 0 1 9 ,2 4 16
解得 a 1,
2
∴抛物线的解析式为 y x
1 9 ,
4 16
y x2 1 1∴抛物线的解析式为 x .
2 2
2 1 1
(2)令 y 0 得到 x x 0 ,
2 2
解得 x 1
1
1 , x2 (舍去),2
故水池的半径至少为 1 米.
十二、问答题
26.如图,在平面直角坐标系 xOy中,直线 y x t与坐标轴交于A 、C两点,经过A 、
C两点的抛物线 y ax2 bx 6与 x轴的另一交点 B的坐标为 2,0 ,连接 BC.
(1)填空: t ______,a ______,b ______;
(2)若点Q在直线 AC下方的抛物线上一动点,连接 AQ、CQ,当 S△AQC 12 ,求点Q的
坐标;
(3)若点Q在直线 AC下方的抛物线上一动点,当CA恰好平分 BCQ时,求点Q横坐标.
1
【答案】(1) 6, 2 ,2
(2)点Q的坐标为 2, 8 或 4, 6 ;
(3)点Q
10
的横坐标为 .
3
【分析】(1)由抛物线解析式可得C 0, 6 ,将C 0, 6 代入直线解析式可得 t 6,
根据直线解析式求出点 A 6,0 ,将 A 6,0 ,B 2,0 代入抛物线 y ax2 bx 6即可求
得 a、b的值;
试卷第 24页,共 29页
2
1 2
( )作QE x轴,交 AC于 E,设Q m,m 2m 6
,则 E m, m 6 ,用m表示出
2
QE的长,再利用三角形面积公式列出一元二次方程方程,解之即可求解;
(3)作 AD x轴,交CQ的延长线于D,则 DAB 90 ,可证 ACD≌ ACB ASA ,
1 1
得到 AD AB 8 2,从而得出点D的坐标,求得CD的解析式,再由 x 6 x 2x 6,
3 2
进行计算即可得到答案.
【详解】(1)解:在 y ax2 bx 6中,当 x 0时, y= 6,
C 0, 6 ,
将C 0, 6 代入 y x t得: t 6,
直线的解析式为: y x 6,
在 y x 6中,当 y 0 时, x 6 0,
解得: x 6,
A 6,0 ,
2 36a 6b 6 0将 A 6,0 , B 2,0 代入 y ax bx 6得:
4a 2b
,
6 0
1
a
解得: 2 ,
b 2
1
故答案为: 6, 2 ,2;
1
(2 2)解:由(1)知抛物线解析式为 y x 2x 6 ,
2
QE x AC
1 2
作 轴,交 于 E,设Q m,m 2m 6 ,则 E m, m 6 ,
2
∴QE m 6
1
m 2 2m 6
1
m
2 3m ,
2 2
1 1 1 2
依题意得 S△AQC QE xA m 3m
6 12,2 2 2
整理得m2 6m 8 0,
解得m 2或m 4,
∴点Q的坐标为 2, 8 或 4, 6 ;
试卷第 25页,共 29页
(3)解:如图,作 AD x轴,交CQ的延长线于D,则 DAB 90 ,
∵ A 6,0 ,C 0, 6 , B 2,0 ,
OA OC 6 , AB 8,
AOC 90 ,
OAC OCA 45 ,
DAC DAB OAC 90 45 45 ,
DAC BAC,
CA平分 BCQ,
DCA BCA,
AC AC,
ACD≌ ACB ASA ,
AD AB 8,
D 6, 8 ,
设直线CD的关系式为: y kx 6,
将D 6, 8 代入可得: 8 6k 6 ,
1
解得: k ,
3
直线CD的关系式为: y
1
x 6 ,
3
1 x 6 1由 x2 2x 6,
3 2
5
解得: x1 0 , x2 ,3
点Q在直线 AC下方的抛物线上一动点,
x 10 ,
3
Q 10点的横坐标为 .
3
【点睛】本题考查了求二次函数和一次函数解析式、角平分线的定义、三角形全等的判
定与性质、解一元二次方程等知识,熟练掌握以上知识点,添加适当的辅助线,是解题
试卷第 26页,共 29页
的关键.
十三、计算题
27.定义:若一个函数图像中存在横、纵坐标相等的点,则称该点为这个函数图像的“等
值点”,例如:点 1,1 是函数 y 2x 1的图像的“等值点”.
(1)分别判断函数 y 2x 1,y x2 x 2的图像上是否存在“等值点” 如果存在,求出“等
值点”的坐标;如果不存在,请说明理由;
9
(2)设函数 y x 0 , y x b x 0 的图像的“等值点”分别为点 A、B,过点 B作
x
BC x轴,垂足为C,当 ABC面积为 3 时,求b的值;
(3) 2若函数 y x 4 x m 的图像记为W1 ,将其沿直线 x m翻折后的图像记为W2 ,当
W,与W2 组合成的图像上恰有两个“等值点”时,请求出m的取值范围.
【答案】(1)函数 y 2x 1的图象上存在“等值点”为 1, 1 ;函数 y x2 x 2的图象上
不存在个“等值点”
(2)b的值为3 33 或3 33
m 17(3) 1 17 1 17或
8 m 2 2
【分析】(1)根据“等值点”的定义建立方程求解即可得出答案;
9
(2)先根据“等值点”的定义求出函数 y x 0 的图象上 “等值点” A 3,3 ,同理求
x
B 1 b, 1 b 1 1 1出 ,根据 ABC的面积为 3 可得 b 3 b 3 ,求解即可;
2 2 2 2 2
1 17 1 17
(3)先求出函数 y x2 4的图象上有两个“等值点” ,2 2
,
1 17 1 17
, ,再利用翻折的性质分类讨论即可.
2 2
【详解】(1)在 y 2x 1中,令 x 2x 1,得 x= 1,
∴函数 y 2x 1的图象上存在“等值点”为 1, 1 ;
在 y x2 x
2
2中,令 x x2 x 2,此时 2 4 1 2 4 0,方程无解,
∴函数 y x2 x 2的图象上不存在个“等值点”;
9 9
(2)在函数 y x 0 中,令 x ,
x x
试卷第 27页,共 29页
解得: x 3,
∴ A 3,3 ,
在函数 y x b中,令 x x b,
1
解得: x b ,
2
B 1∴ b,
1 b ,
2 2
∵ BC x轴,
B 1∴ b,0
,
2
∴ BC
1
b ,
2
∵ ABC的面积为 3,
1 1
∴ b
1
3 b 3 ,
2 2 2
当 b<0时,b2 6b 24 0,
解得b 3 33 ,
当0 b 6时,b2 6b 24 0,
∵ 6 2 4 1 24 60 0,
∴方程b2 6b 24 0没有实数根,
当 b 6时,b2 6b 24 0,
解得:b 3 33 ,
综上所述,b的值为3 33 或3 33 ;
(3)令 x x2 4,
x 1 17 x 1 17解得: 1 , ,2 2 2
1 17 1 17 1 17 1 17
∴函数 y x2 4的图象上有两个“等值点” ,2 2
, , ,
2 2
1 17 1 17
①当m 1 17 时,W1,W2两部分组成的图象上必有 2 个“等值点” , ,2 2 2
1 17 1 17
,2 2
,
将函数 y x2 4 x m 的图像沿直线 x m翻折后为: y x 2m 2 4 x<m ,
令 x x 2m 2 4,
试卷第 28页,共 29页
整理得: x2 (4m 1)x 4m2 4 0,
∵W2 的图象上不存在“等值点”,
∴Δ 0,
∴ 4m 1 2 4 4m2 4 0 ,
∴m
17
,
8
1 17 1 17 1 17 1 17 1 17
②当m 时,有 3 个“等值点” , , , ,2 2 2 2 2
1 17 1 17
, ,,
2 2
1 17 m 1 17③当 时,W1,W2 两部分组成的图象上恰有 2 个“等值点”,
2 2
1 17 1 17 1 17
④当m 时,W1,W2 两部分组成的图象上恰有 1 个“等值点” , ,
2 2 2
m 1 17⑤当 时,W1,W2 两部分组成的图象上没有“等值点”,
2
17
综上所述,当W1,W2 两部分组成的图象上恰有 2 个“等值点”时,m 或8
1 17 m 1 17 .
2 2
【点睛】本题考查了一次函数,反比例函数,二次函数与新定义“等值点”综合运用,一
元二次方程根的判别式,翻折的性质等,解题关键是理解并运用新定义,运用分类讨论
思想解决问题.
试卷第 29页,共 29页
2023-2024 学年九年级上学期期中数学试题
一、单选题
1.下列方程是一元二次方程的是( )
A. x2
1
2xy 5 B 2. x 2
x
C. x2 y2 6 D. x2 5
2.抛物线 y 2x2 的对称轴是直线( )
A. y 0 B. y 1 C. x 0 D. x 2
3.用配方法解方程 x2 6x 4 0,原方程应变为( )
A. (x 3)2 13 B. (x 3)2 5 C. (x 3)2 13 D. (x 3)2 5
4.如图,点 A,B,C,D在 O上, AOC 142 ,点 B是 AC的中点,则 D的度数
是( )
A.70 B.55 C. 35.5 D.35
5.由二次函数 y=(2 x﹣3)2 1,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线 x=﹣3
C.其最小值为 1 D.当 x<3 时,y随 x的增大而增大
6.如图所示的网格由边长相同的小正方形组成,点 A、B、C、D、E、F 在小正方形的
顶点上,则△ABC 的外心是( )
A.点 D B.点 E C.点 F D.点 G
试卷第 1页,共 29页
7.某校九年级各班进行拔河比赛,每两个班之间都要赛一场,共赛 28 场.设共有 x个班
参赛,根据题意可列方程为( )
x x 1 28 xA B x 1 x x 1 . . 28 C. 28 D. x x 1 28
2 2
8 x AB C : y x2.如图,垂直于 轴的直线 分别与抛物线 1 x 0 和抛物线
2
C2 : y
x
x 0 交于 A,B两点,过点 A作CD∥ x轴分别与 y轴和抛物线C2 交于点 C,9
S
D,过点 B EF x OFB作 ∥ 轴分别与 y轴和抛物线C1交于点 E,F,则 S 的值为( ) EAD
3 1 1 1A. B. C. D.
9 24 9 64
二、填空题
9.抛物线 y (x 2)2 6顶点坐标是 .
10.已知关于 x的一元二次方程 x2 ax 1 0有两个相等的实数根,则 a的值是 .
11.把二次函数 y x2 的图像向左平移 1 个单位,然后向上平移 3 个单位,则平移后
的图像对应的二次函数的关系式为 .
12.已知二次函数 y=ax2+bx+c(a>0)图象的对称轴为直线 x=1,且经过点(﹣1,y1),(2,
y2),则 y1 y2.(填“>”“<”或“=”)
13.二次函数 y ax2 bx c的图象如图所示,直接写出不等式 ax2 bx c 0的解集
为 .
14.将半径为 5 的 O如图折叠,折痕 AB长为 6,C为折叠后 AB的中点,则OC长
试卷第 2页,共 29页
为 .
15.对于两个不相等的实数 a、b,我们规定符号Max{a,b}表示 a、b中的较大值,如:
Max{1,3} 3,按照这个规定,方程Max{1,x} x 2 6 的解为 .
16.如图,正方形OABC的边长为 4,OA与 x轴负半轴的夹角为15 ,点 B在抛物线
y ax 2 a 0 的图象上,则 a的值为 .
三、计算题
17.解方程:
(1) x 5 2 16;
(2) 2x2 1 4x.
(3)5x x 1 2 x 1
(4) 2x2 x 1 0.
四、作图题
18.已知二次函数 y x2 2x 3.
试卷第 3页,共 29页
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值 y为正数时,自变量 x的取值范围;
②当 2 x 2时,函数值 y的取值范围.
五、问答题
19 2.已知关于 x的一元二次方程 a c x 2bx a c 0,其中 a,b,c为 ABC的三
边.
(1)若 x 1是方程的根,判断 ABC的形状,并说明理由;
(2)若方程有两个相等的实数根,判断 ABC的形状,并说明理由.
六、证明题
20.如图,点 A,B,C,D在 O上,且 AB = D C,判断 AC与 BD的数量关系.
七、问答题
21.如图,若二次函数 y=x2﹣x﹣2 的图象与 x轴交于 A,B两点(点 A在点 B的左侧),
与 y轴交于 C点.
(1)求 A,B两点的坐标;
(2)若 P(m,﹣2)为二次函数 y=x2﹣x﹣2 图象上一点,求 m的值.
试卷第 4页,共 29页
八、应用题
22.某品牌服装平均每天可以售出 10 件,每件盈利 40 元.受新冠肺炎疫情影响,商场
决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:每件服装每降价
1 元,平均每天就可以多售出 2 件,如果需要盈利 700 元,那么每件降价多少元
九、证明题
23.如图,⊙O的直径 AB为 6cm,∠ACB的平分线交⊙O于点 D.
(1)判断 ADB的形状,并证明;
(2)求 BD的长.
十、应用题
24.某农场要建一个矩形动物场,场地的一边靠墙(墙 AB长度小于 10 米),另外三边
用木栏围成,木栏总长 20 米,设动物场CD边的长为 xm ,矩形面积为 ym2 .
(1)矩形面积 y ______(用含 x的代数式表示);
(2)当矩形动物场面积为48m2 时,求CD边的长;
(3)能否围成面积为52m2 矩形动物场 说明理由.
试卷第 5页,共 29页
十一、计算题
25.如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,OA 2m ,从A 处
向外喷出的水流在各个方向上沿形状相同的抛物线路径落下.王丽芳同学根据题意在图
中建立如图所示的坐标系,水流喷出的高度 y m 与水平距离 x m 之间的关系式是
y ax 2 bx c x 0 1,已知水流的最高点到OA的水平距离是 m ,最高点离水面是
2
9 m .
4
求二次函数表达式;
(1)若不计其他因素,水池的半径至少为多少米,才能使喷出的水流不至于落在池外
十二、问答题
26.如图,在平面直角坐标系 xOy中,直线 y x t与坐标轴交于A 、C两点,经过A 、
C两点的抛物线 y ax2 bx 6与 x轴的另一交点 B的坐标为 2,0 ,连接 BC.
(1)填空: t ______,a ______,b ______;
(2)若点Q在直线 AC下方的抛物线上一动点,连接 AQ、CQ,当 S△AQC 12 ,求点Q的
坐标;
(3)若点Q在直线 AC下方的抛物线上一动点,当CA恰好平分 BCQ时,求点Q横坐标.
十三、计算题
27.定义:若一个函数图像中存在横、纵坐标相等的点,则称该点为这个函数图像的“等
值点”,例如:点 1,1 是函数 y 2x 1的图像的“等值点”.
试卷第 6页,共 29页
(1)分别判断函数 y 2x 1,y x2 x 2的图像上是否存在“等值点” 如果存在,求出“等
值点”的坐标;如果不存在,请说明理由;
9
(2)设函数 y x 0 , y x b x 0 的图像的“等值点”分别为点 A、B,过点 B作
x
BC x轴,垂足为C,当 ABC面积为 3 时,求b的值;
(3) 2若函数 y x 4 x m 的图像记为W1 ,将其沿直线 x m翻折后的图像记为W2 ,当
W,与W2 组合成的图像上恰有两个“等值点”时,请求出m的取值范围.
试卷第 7页,共 29页
江苏省苏州市苏州工业园区星湾学校
2023-2024 学年九年级上学期期中数学试题
一、单选题
1.下列方程是一元二次方程的是( )
A. x2
1
2xy 5 B x2. 2
x
C. x2 y2 6 D. x2 5
【答案】D
【分析】直接根据一元二次方程的定义逐项判断即可.
【详解】解:A、 x2 2xy 5 中含有两个未知数,不是一元二次方程,故本选项不符合
题意;
B x2
1
、 2是分式方程,不是一元二次方程,故本选项不符合题意;
x
C、 x2 y2 6中含有两个未知数,不是一元二次方程,故本选项不符合题意;
D、 x2 5,是一元二次方程,故本选项符合题意;
故选:D.
【点睛】本题考查了一元二次方程的定义,只含有一个未知数,并且所含未知数的项的
最高次数是 2 的整式方程叫一元二次方程,熟练掌握此定义是解题的关键.
2.抛物线 y 2x2 的对称轴是直线( )
A. y 0 B. y 1 C. x 0 D. x 2
【答案】C
【分析】根据抛物线解析式,可直接求出对称轴.
【详解】解: 抛物线解析式为 y 2x2 ,
对称轴为 x 0.
故选:C.
2
【点睛】本题考查二次函数的性质,解题的关键是记住二次函数 y = ax (a 0)的对称
轴是直线 x 0.
3.用配方法解方程 x2 6x 4 0,原方程应变为( )
A. (x 3)2 13 B. (x 3)2 5 C. (x 3)2 13 D. (x 3)2 5
【答案】D
【分析】先将常数项移到右边,两边再同时加上一次项系数一半的平方进行配方即可得
试卷第 8页,共 29页
到答案.
【详解】对 x2 6x 4 0进行配方:
移项,得: x2 6x 4,
6
2
两边同时加上一次项系数一半的平方,即 9,得:
2
x2 6x 9 4 9 ,
2
整理,得: x 3 5,
故选:D.
【点睛】本题考查一元二次方程的配方,熟练掌握配方的过程是本题的解题关键.
4.如图,点 A,B,C,D在 O上, AOC 142 ,点 B是 AC的中点,则 D的度数
是( )
A.70 B.55 C. 35.5 D.35
【答案】C
【分析】本题主要考查的是圆心角、弧、弦的关系定理、圆周角定理.根据圆心角、弧、
1
弦的关系定理得到 AOB AOC2 ,再根据圆周角定理解答.
【详解】解:连接OB,如图所示:
∵点 B是 AC的中点,
∴ AOB
1
AOC 71 ,
2
试卷第 9页,共 29页
1
由圆周角定理得, D AOB 35.5 ,故 C 正确.
2
故选:C.
5.由二次函数 y=(2 x﹣3)2 1,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线 x=﹣3
C.其最小值为 1 D.当 x<3 时,y随 x的增大而增大
【答案】C
【分析】由解析式可知 a>0,对称轴为 x=3,最小值为 0,在对称轴的左侧 y随 x的增
大而减小,可得出答案.
【详解】由二次函数 y=(2 x﹣3)2 1,可知:
A:∵a>0,其图象的开口向上,故此选项错误;
B.∵其图象的对称轴为直线 x=3,故此选项错误;
C.其最小值为 1,故此选项正确;
D.当 x<3 时,y随 x的增大而减小,故此选项错误.
故选:C.
【点睛】本题主要考查二次函数的性质,掌握二次函数的开口方向、对称轴、顶点坐标、
最大值及对称轴两侧的增减性是解题的关键.属于基础题目.
6.如图所示的网格由边长相同的小正方形组成,点 A、B、C、D、E、F 在小正方形的
顶点上,则△ABC 的外心是( )
A.点 D B.点 E C.点 F D.点 G
【答案】A
【分析】根据三角形三边中垂线相交于一点,这一点叫做它的外心,据此解答即可.
【详解】根据图形可知,直线 DG 是△ABC 的 BC 边上的中垂线,点 D 在△ABC 的 AB
边上的中垂线上,
∴点 D 是△ABC 外心.
故选:A.
【点睛】本题主要考查了三角形的外心的定义,注意:三角形三边中垂线相交于一点,
试卷第 10页,共 29页
这一点是此三角形的外心.
7.某校九年级各班进行拔河比赛,每两个班之间都要赛一场,共赛 28 场.设共有 x个班
参赛,根据题意可列方程为( )
A. x x 1 28 x x 1B x x 1C . 28 . 28 D. x x 1 28
2 2
【答案】C
【分析】根据互动问题直接列式即可得到答案;
【详解】解:由题意可得,
x x 1
28,
2
故选:C;
【点睛】本题考查一元二次方程解应用题,解题的关键是互动问题注意重复问题.
8 2.如图,垂直于 x轴的直线 AB分别与抛物线C1 : y x x 0 和抛物线
2
C2 : y
x
x 0 交于 A,B两点,过点 A作CD∥ x轴分别与 y轴和抛物线C2 交于点 C,9
S
D,过点 B作 EF OFB∥ x轴分别与 y轴和抛物线C1交于点 E,F,则 S 的值为( ) EAD
3 1 1 1A. B. C. D.
9 24 9 64
【答案】B
【分析】此题重点考查学生对二次函数的图象和性质的应用能力.根据二次函数的图象
和性质结合三角形面积公式求解.
a2
【详解】解:设点 A,B横坐标为 a,则点A 纵坐标为 a 2 ,点 B的纵坐标为 ,
9
BE∥ x轴,
F a
2
∴点 纵坐标为 ,
9
∵点 F 是抛物线 y = x2上的点,
1
∴点 F 横坐标为 x y a,
3
CD x轴,
试卷第 11页,共 29页
∴点D纵坐标为 a 2 ,
x2
∵点D是抛物线 y 上的点,
9
∴点D横坐标为 x 9y 3a,
AD 2a,BF 2 a CE 8 a2 OE 1 , , a2 ,
3 9 9
1 BF OE 1S OFB 2 27 1 1 ,S EAD AD CE 8 24
2 9
故选:B.
二、填空题
9.抛物线 y (x 2)2 6顶点坐标是 .
【答案】 ( 2,6)
【分析】本题考查了求二次函数的性质,根据抛物线的顶点式直接求得顶点坐标.
【详解】抛物线 y (x 2)2 6的顶点坐标是 ( 2,6) ,
故答案为: ( 2,6) .
10.已知关于 x的一元二次方程 x2 ax 1 0有两个相等的实数根,则 a的值是 .
【答案】 2
【分析】本题主要考查根的判别式,根据方程有两个相等的实数根时 b2 4ac 0列
出方程,解之可得答案.
【详解】解:∵关于 x的一元二次方程 x2 ax 1 0有两个相等的实数根,
2
∴ a 4 1 1 0 ,即 a 2 4 0
解得, a 2,
故答案为: 2.
11.把二次函数 y x2 的图像向左平移 1 个单位,然后向上平移 3 个单位,则平移后
的图像对应的二次函数的关系式为 .
2
【答案】 y x 1 3
【分析】直接运用平移规律“左加右减,上加下减”解答.
【详解】解:把二次函数 y x2 的图像向左平移 1 个单位,然后向上平移 3 个单位得
2
到的二次函数的关系式为 y x 1 3 ,
试卷第 12页,共 29页
故答案为: y x 1 2 3 .
【点睛】本题主要考查了二次函数图象的平移,要求熟练掌握平移的规律:左加右减,
上加下减.
12.已知二次函数 y=ax2+bx+c(a>0)图象的对称轴为直线 x=1,且经过点(﹣1,y1),(2,
y2),则 y1 y2.(填“>”“<”或“=”)
【答案】>
【分析】根据二次函数 y=ax2+bx+c(a>0)图象的对称轴为直线 x=1,且经过点(﹣1,y1),
(2,y2)和二次函数的性质可以判断 y1 和 y2的大小关系.
【详解】解:∵二次函数 y=ax2+bx+c(a>0)图象的对称轴为直线 x=1,
∴当 x>1 时,y随 x的增大而增大,当 x<1 时,y随 x的增大而减小,
∵该函数经过点(﹣1,y1),(2,y2),|﹣1﹣1|=2,|2﹣1|=1,
∴y1>y2,
故答案为:>.
【点睛】本题考查了二次函数的增减性问题,掌握二次函数的性质是解题的关键.
13.二次函数 y ax2 bx c的图象如图所示,直接写出不等式 ax2 bx c 0的解集
为 .
【答案】 2 x 6
【分析】根据二次函数图像找到 x轴上方图像 x取值范围即可得到答案.
【详解】解:由二次函数图像可得,
当 2 x 6 时, y 0 ,
故答案为: 2 x 6 .
【点睛】本题考查根据二次函数图像解一元二次不等式,解题的关键是熟练掌握二次函
数与一元二次不等式的关系.
14.将半径为 5 的 O如图折叠,折痕 AB长为 6,C为折叠后 AB的中点,则OC长
为 .
试卷第 13页,共 29页
【答案】3
【分析】本题考查了垂径定理,圆心角、弧、弦的关系和勾股定理.延长OC交 O于
D点,交 AB于 E点,连接OA、OB、AC、BC ,如图根据圆心角、弧、弦的关系由 AC B C
得到CA CB,则可判断OC垂直平分 AB,则 AE BE 3,再利用勾股定理计算出
OE 4 ,所以DE 1,然后利用 C点和 D点关于 AB对称得到CE 1,最后计算OE CE
即可.
【详解】解:延长OC交 O于 D点,交 AB于 E点,连接OA、OB、AC、BC,如图,
∵C为折叠后 AB的中点,
∴ AC B C,
∴CA CB,
∵OA OB,
∴OC垂直平分 AB,
1
∴AE BE AB 3,
2
在Rt△AOE中,OE OA2 AE2 52 32 4,
∴DE OD OE 5 4 1,
∵ ADB沿 AB折叠得到 A CB,CD垂直 AB,
∴C点和 D点关于 AB对称,
∴CE=DE=1,
∴OC OE CE 4 1 3.
故答案为:3.
15.对于两个不相等的实数 a、b,我们规定符号Max{a,b}表示 a、b中的较大值,如:
Max{1,3} 3,按照这个规定,方程Max{1,x} x 2 6 的解为 .
【答案】 x 3或 x 7
试卷第 14页,共 29页
【分析】分类讨论 x的范围,利用题中的新定义,列出方程,解方程即可.
【详解】解:当 x 1时,方程为: x2 6 x
即 x2 x 6 0,
解得: x1 2 (舍去), x2 3;
∴此时 x 3,
当 x 1时,方程为: x2 6 1,
解得: x1 7 (舍去), x2 7 ,
∴ x 7 ;
故答案为: x 3或 x 7 .
【点睛】本题主要考查了解一元二次方程,新定义实数运算,解题的关键是理解题意,
列出方程求解.
16.如图,正方形OABC的边长为 4,OA与 x轴负半轴的夹角为15 ,点 B在抛物线
y ax 2 a 0 的图象上,则 a的值为 .
2
【答案】
12
【分析】本题主要考查了正方形的性质、直角三角形的性质以及用待定系数法确定函数
解析式的方法,连接OB,过 B作 BD x轴于 D,若OA与 x轴负半轴的夹角为15 ,那
么 BOD 30 ;在正方形OABC中,已知了边长,易求得对角线OB的长,进而可在
Rt△OBD中求得 BD、OD的值,也就得到了 B点的坐标,然后将其代入抛物线的解析
式中,即可求得待定系数 a的值.
【详解】解:如图,连接OB,过 B作 BD x轴于 D;
则 BOA 45 , BOD 30 ;
试卷第 15页,共 29页
已知正方形的边长为 4,则OB 4 2 ;
Rt△OBD中,OB 4 2 , BOD 30 ,
BD 1则 OB 2 2,OD OB2 BD2 2 6 ;
2
故 B 2 6, 2 2 ,
2
代入抛物线的解析式中,得: 2 6 a 2 2 ,
2
解得 a ,
12
2
故答案为: .
12
三、计算题
17.解方程:
(1) x 5 2 16;
(2) 2x2 1 4x.
(3)5x x 1 2 x 1
(4) 2x2 x 1 0.
【答案】(1) x 9, x2 1
(2) x1 1
6
, x2 1
6
2 2
(3) x1 1, x
2
2 5
1
(4) x1 1, x2 2
【分析】本题主要考查解一元二次方程的能力:
(1)利用直接开平方法求解即可;
(2)利用配方法求解即可;
(3)先移项,再将左边利用提公因式法因式分解,继而可得两个关于 x的一元一次方
程,分别求解即可得出答案;
(4)利用公式法求解可得方程的解.
2
【详解】(1)∵ x 5 16,
∴ x 5 4,
∴ x 9 , x2 1;
试卷第 16页,共 29页
(2) 2x2 1 4x,
2x2 4x 1 0,
x2 1 2x 0,
2
x2 2x 1 ,
2
x2 2x 1 3 ,
2
x 1 2 3 ,
2
x 1 6 ,
2
6 6
∴ x1 1 , x2 1 ;2 2
(3)5x x 1 2 x 1 ,
5x x 1 2 x 1 0,
(x 1)(5x 2) 0
x 1 0或5x 2 0,
2
∴ x1 1, x2 5 ;
(4) 2x2 x 1 0,
这里 a 2,b = -1,c 1,
△ 1 2 4 2 1 9 0 ,
b b2 4ac 1 9x 1 3则 ,
2a 4 4
∴ x1 1, x
1
2 .2
【点睛】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方
法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的
方法是解题的关键.
四、作图题
18.已知二次函数 y=﹣x2+2x+3.
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值 y 为正数时,自变量 x 的取值范围;
②当﹣2<x<2 时,函数值 y 的取值范围.
试卷第 17页,共 29页
【答案】(1)见解析;(2)①﹣1<x<3;②﹣5<y<4.
【详解】(1)配方后即可确定顶点坐标及对称轴;
(2)确定顶点坐标及对称轴、与坐标轴的交点坐标即可确定抛物线的解析式;
(3)根据图象利用数形结合的方法确定答案即可;
五、问答题
19 2.已知关于 x的一元二次方程 a c x 2bx a c 0,其中 a,b,c为 ABC的三
边.
(1)若 x 1是方程的根,判断 ABC的形状,并说明理由;
(2)若方程有两个相等的实数根,判断 ABC的形状,并说明理由.
【答案】(1)等腰三角形,理由见解析
(2)直角三角形,理由见解析
【分析】(1)根据方程的解把 x=1 代入方程得到 c﹣b=0,即 c=b,于是由等腰三角形的
判定即可得到 ABC是等腰三角形;
(2)根据根的判别式得出 a,b,c的关系,即可根据勾股定理的逆定理判断△ABC的
形状.
【详解】(1)解:把 x=1 代入方程得,
a c 2b a c 0 ,
化简得 c b,
则该三角形 ABC的形状为等腰三角形.
(2)解:由题意可得方程有两个相等的实数根
2 2
则 a c x 2bx a c 0的判别式:Δ 2b 4 a c a c 0
4b2 4 (c2 a2) 0
试卷第 18页,共 29页
化简可得b2 a2 c2
则该三角形 ABC的形状为直角三角形.
【点睛】本题考查了根的判别式以及一元二次方程、等腰三角形的判定、直角三角形的
判定,掌握一元二次方程根的判别式是解题的关键.
六、证明题
20.如图,点 A,B,C,D在 O上,且 AB = D C,判断 AC与 BD的数量关系.
【答案】 AC BD
【分析】本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦
中有一组量相等,则另外两组量也对应相等.由 AB = D C,可得 AB+ B C = D C + B C,
即 AC B D,因此 AC与 BD相等.
【详解】解: AC BD.理由如下:
∵ AB = D C,
∴ AB+ B C = D C + B C,
即 AC B D,
∴ AC BD.
七、问答题
21.如图,若二次函数 y=x2﹣x﹣2 的图象与 x轴交于 A,B两点(点 A在点 B的左侧),
与 y轴交于 C点.
(1)求 A,B两点的坐标;
(2)若 P(m,﹣2)为二次函数 y=x2﹣x﹣2 图象上一点,求 m的值.
试卷第 19页,共 29页
【答案】(1)A(-1,0),B(2,0);(2)m的值为 0 或 1.
【分析】(1)解方程 x2-x-2=0 可得 A,B两点的坐标;
(2)把 P(m,-2)代入 y=x2-x-2 得 m2-m-2=-2,然后解关于 m的方程即可.
【详解】解:(1)当 y=0 时,x2-x-2=0,解得 x1=-1,x2=2,
∴A(-1,0),B(2,0);
(2)把 P(m,-2)代入 y=x2-x-2 得 m2-m-2=-2,
解得 m1=0,m2=1,
∴m的值为 0 或 1.
【点睛】本题考查了抛物线与 x轴的交点:把求二次函数 y=ax2+bx+c(a,b,c是常数,
a≠0)与 x轴的交点坐标问题转化为解关于 x的一元二次方程.
八、应用题
22.某品牌服装平均每天可以售出 10 件,每件盈利 40 元.受新冠肺炎疫情影响,商场
决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:每件服装每降价
1 元,平均每天就可以多售出 2 件,如果需要盈利 700 元,那么每件降价多少元
【答案】每件降价5元或30元.
【分析】本题考查了一元二次方程的应用.设每件降价 x元,则每件盈利 40 x 元,
平均每天可售出 10 2x 件,利用总利润=每件盈利×平均每天的销售量,即可得出关
于 x的一元二次方程,解之即可得出结论.
【详解】解:设每件降价 x元,则每件盈利 40 x 元,
依题意得: 40 x 10 2x 700,
整理得: x2 35x 150 8,
解得: x1 5, x2 30.
答:每件降价5元或30元.
试卷第 20页,共 29页
九、证明题
23.如图,⊙O的直径 AB为 6cm,∠ACB的平分线交⊙O于点 D.
(1)判断 ADB的形状,并证明;
(2)求 BD的长.
【答案】(1)等腰直角三角形,见解析;(2)3 2
【分析】(1)先根据角平分线定义得∠ACD = ∠DCB,再利用圆周角定理得∠ACD =
∠ABD,∠DCB = ∠DAB,等量代换即可求解,
(2)利用直径和勾股定理即可得出答案.
【详解】(1)△ADB是等腰直角三角形.
证明:∵CD平分∠ACB,
∴ ∠ACD = ∠DCB.
∵ ∠ACD = ∠ABD,∠DCB = ∠DAB,
∴ ∠ABD = ∠DAB.
∴AD=BD.
∵AB是直径,
∴∠ADB=90°
∴△ADB是等腰直角三角形
(2)在 Rt△ADB中, AD2+BD2=AB2,
∴2BD2=AB2,
∴BD= 2 AB= 2 ×6= 3 2 (cm)
2 2
【点睛】此题考查了圆周角定理、等腰直角三角形的判定与性质以及勾股定理等知识,
熟练掌握圆周角定理和等腰直角三角形的判定与性质是解题的关键.
试卷第 21页,共 29页
十、应用题
24.某农场要建一个矩形动物场,场地的一边靠墙(墙 AB长度小于 10 米),另外三边
用木栏围成,木栏总长 20 米,设动物场CD边的长为 xm ,矩形面积为 ym2 .
(1)矩形面积 y ______(用含 x的代数式表示);
(2)当矩形动物场面积为48m2 时,求CD边的长;
(3)能否围成面积为52m2 矩形动物场 说明理由.
【答案】(1) 2x2 20x m2
(2) 6m
(3)不能,理由见解析
【分析】本题考查了列代数式和一元二次方程的应用.
(1)根据矩形的面积=长×宽求解即可;
(2)根据矩形动物场面积为 48m2 ,列一元二次方程,求解即可;
(3)根据矩形动物场面积为52m2 列一元二次方程,求解即可.
【详解】(1)∵动物场CD边的长为 xm ,木栏总长 20 米,则 EF CD xm,
∴DE 20 2x 米,
y CD DE x 20 2x 2x2∴矩形面积为 20x m2 ,
2x2 20x m2故答案为: ;
(2)根据题意,得 2x2 20x 48 ,
解得 x1 4,x2 6,
∵墙 AB长度小于10m,
∴当CD 4m时,DE 20 2 4 12m 10m ,不符合题意;
当CD 6m时,DE 20 2 6 8m 10m ,符合题意;
所以,CD边的长为6m;
(3)不能,理由如下:
试卷第 22页,共 29页
根据题意,得 2x2 20x 52,
整理,得 x2 10x 26 0,
∵ 100 4 1 26 4 0,
∴方程没有实数根,
∴不能围成面积为52m2 矩形动物场.
十一、计算题
25.如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,OA 2m ,从A 处
向外喷出的水流在各个方向上沿形状相同的抛物线路径落下.王丽芳同学根据题意在图
中建立如图所示的坐标系,水流喷出的高度 y m 与水平距离 x m 之间的关系式是
y ax 2 bx c x 0 1,已知水流的最高点到OA的水平距离是 m ,最高点离水面是
2
9 m .
4
求二次函数表达式;
(1)若不计其他因素,水池的半径至少为多少米,才能使喷出的水流不至于落在池外
y x2 1【答案】(1) x
1
2 2
(2)水池的半径至少为 1 米
【分析】本题考查了待定系数法求解析式,二次函数的实际应用.
(1)根据抛物线的顶点式求解即可.
(2)令 y 0 得到 x2
1 x 1 0 求得抛物线与 x轴正半轴的交点坐标,其横坐标就是
2 2
所求.
1 9 1
【详解】(1)∵水流的最高点到OA的水平距离是 m ,最高点离水面是 m,OA m ,
4 16 2
1 9 1
∴抛物线的顶点坐标为 , , A 0, ,
4 16 2
1 2 9
故设抛物线的解析式为 y a x ,
4 16
试卷第 23页,共 29页
1 2
∴ a 0 1 9 ,2 4 16
解得 a 1,
2
∴抛物线的解析式为 y x
1 9 ,
4 16
y x2 1 1∴抛物线的解析式为 x .
2 2
2 1 1
(2)令 y 0 得到 x x 0 ,
2 2
解得 x 1
1
1 , x2 (舍去),2
故水池的半径至少为 1 米.
十二、问答题
26.如图,在平面直角坐标系 xOy中,直线 y x t与坐标轴交于A 、C两点,经过A 、
C两点的抛物线 y ax2 bx 6与 x轴的另一交点 B的坐标为 2,0 ,连接 BC.
(1)填空: t ______,a ______,b ______;
(2)若点Q在直线 AC下方的抛物线上一动点,连接 AQ、CQ,当 S△AQC 12 ,求点Q的
坐标;
(3)若点Q在直线 AC下方的抛物线上一动点,当CA恰好平分 BCQ时,求点Q横坐标.
1
【答案】(1) 6, 2 ,2
(2)点Q的坐标为 2, 8 或 4, 6 ;
(3)点Q
10
的横坐标为 .
3
【分析】(1)由抛物线解析式可得C 0, 6 ,将C 0, 6 代入直线解析式可得 t 6,
根据直线解析式求出点 A 6,0 ,将 A 6,0 ,B 2,0 代入抛物线 y ax2 bx 6即可求
得 a、b的值;
试卷第 24页,共 29页
2
1 2
( )作QE x轴,交 AC于 E,设Q m,m 2m 6
,则 E m, m 6 ,用m表示出
2
QE的长,再利用三角形面积公式列出一元二次方程方程,解之即可求解;
(3)作 AD x轴,交CQ的延长线于D,则 DAB 90 ,可证 ACD≌ ACB ASA ,
1 1
得到 AD AB 8 2,从而得出点D的坐标,求得CD的解析式,再由 x 6 x 2x 6,
3 2
进行计算即可得到答案.
【详解】(1)解:在 y ax2 bx 6中,当 x 0时, y= 6,
C 0, 6 ,
将C 0, 6 代入 y x t得: t 6,
直线的解析式为: y x 6,
在 y x 6中,当 y 0 时, x 6 0,
解得: x 6,
A 6,0 ,
2 36a 6b 6 0将 A 6,0 , B 2,0 代入 y ax bx 6得:
4a 2b
,
6 0
1
a
解得: 2 ,
b 2
1
故答案为: 6, 2 ,2;
1
(2 2)解:由(1)知抛物线解析式为 y x 2x 6 ,
2
QE x AC
1 2
作 轴,交 于 E,设Q m,m 2m 6 ,则 E m, m 6 ,
2
∴QE m 6
1
m 2 2m 6
1
m
2 3m ,
2 2
1 1 1 2
依题意得 S△AQC QE xA m 3m
6 12,2 2 2
整理得m2 6m 8 0,
解得m 2或m 4,
∴点Q的坐标为 2, 8 或 4, 6 ;
试卷第 25页,共 29页
(3)解:如图,作 AD x轴,交CQ的延长线于D,则 DAB 90 ,
∵ A 6,0 ,C 0, 6 , B 2,0 ,
OA OC 6 , AB 8,
AOC 90 ,
OAC OCA 45 ,
DAC DAB OAC 90 45 45 ,
DAC BAC,
CA平分 BCQ,
DCA BCA,
AC AC,
ACD≌ ACB ASA ,
AD AB 8,
D 6, 8 ,
设直线CD的关系式为: y kx 6,
将D 6, 8 代入可得: 8 6k 6 ,
1
解得: k ,
3
直线CD的关系式为: y
1
x 6 ,
3
1 x 6 1由 x2 2x 6,
3 2
5
解得: x1 0 , x2 ,3
点Q在直线 AC下方的抛物线上一动点,
x 10 ,
3
Q 10点的横坐标为 .
3
【点睛】本题考查了求二次函数和一次函数解析式、角平分线的定义、三角形全等的判
定与性质、解一元二次方程等知识,熟练掌握以上知识点,添加适当的辅助线,是解题
试卷第 26页,共 29页
的关键.
十三、计算题
27.定义:若一个函数图像中存在横、纵坐标相等的点,则称该点为这个函数图像的“等
值点”,例如:点 1,1 是函数 y 2x 1的图像的“等值点”.
(1)分别判断函数 y 2x 1,y x2 x 2的图像上是否存在“等值点” 如果存在,求出“等
值点”的坐标;如果不存在,请说明理由;
9
(2)设函数 y x 0 , y x b x 0 的图像的“等值点”分别为点 A、B,过点 B作
x
BC x轴,垂足为C,当 ABC面积为 3 时,求b的值;
(3) 2若函数 y x 4 x m 的图像记为W1 ,将其沿直线 x m翻折后的图像记为W2 ,当
W,与W2 组合成的图像上恰有两个“等值点”时,请求出m的取值范围.
【答案】(1)函数 y 2x 1的图象上存在“等值点”为 1, 1 ;函数 y x2 x 2的图象上
不存在个“等值点”
(2)b的值为3 33 或3 33
m 17(3) 1 17 1 17或
8 m 2 2
【分析】(1)根据“等值点”的定义建立方程求解即可得出答案;
9
(2)先根据“等值点”的定义求出函数 y x 0 的图象上 “等值点” A 3,3 ,同理求
x
B 1 b, 1 b 1 1 1出 ,根据 ABC的面积为 3 可得 b 3 b 3 ,求解即可;
2 2 2 2 2
1 17 1 17
(3)先求出函数 y x2 4的图象上有两个“等值点” ,2 2
,
1 17 1 17
, ,再利用翻折的性质分类讨论即可.
2 2
【详解】(1)在 y 2x 1中,令 x 2x 1,得 x= 1,
∴函数 y 2x 1的图象上存在“等值点”为 1, 1 ;
在 y x2 x
2
2中,令 x x2 x 2,此时 2 4 1 2 4 0,方程无解,
∴函数 y x2 x 2的图象上不存在个“等值点”;
9 9
(2)在函数 y x 0 中,令 x ,
x x
试卷第 27页,共 29页
解得: x 3,
∴ A 3,3 ,
在函数 y x b中,令 x x b,
1
解得: x b ,
2
B 1∴ b,
1 b ,
2 2
∵ BC x轴,
B 1∴ b,0
,
2
∴ BC
1
b ,
2
∵ ABC的面积为 3,
1 1
∴ b
1
3 b 3 ,
2 2 2
当 b<0时,b2 6b 24 0,
解得b 3 33 ,
当0 b 6时,b2 6b 24 0,
∵ 6 2 4 1 24 60 0,
∴方程b2 6b 24 0没有实数根,
当 b 6时,b2 6b 24 0,
解得:b 3 33 ,
综上所述,b的值为3 33 或3 33 ;
(3)令 x x2 4,
x 1 17 x 1 17解得: 1 , ,2 2 2
1 17 1 17 1 17 1 17
∴函数 y x2 4的图象上有两个“等值点” ,2 2
, , ,
2 2
1 17 1 17
①当m 1 17 时,W1,W2两部分组成的图象上必有 2 个“等值点” , ,2 2 2
1 17 1 17
,2 2
,
将函数 y x2 4 x m 的图像沿直线 x m翻折后为: y x 2m 2 4 x<m ,
令 x x 2m 2 4,
试卷第 28页,共 29页
整理得: x2 (4m 1)x 4m2 4 0,
∵W2 的图象上不存在“等值点”,
∴Δ 0,
∴ 4m 1 2 4 4m2 4 0 ,
∴m
17
,
8
1 17 1 17 1 17 1 17 1 17
②当m 时,有 3 个“等值点” , , , ,2 2 2 2 2
1 17 1 17
, ,,
2 2
1 17 m 1 17③当 时,W1,W2 两部分组成的图象上恰有 2 个“等值点”,
2 2
1 17 1 17 1 17
④当m 时,W1,W2 两部分组成的图象上恰有 1 个“等值点” , ,
2 2 2
m 1 17⑤当 时,W1,W2 两部分组成的图象上没有“等值点”,
2
17
综上所述,当W1,W2 两部分组成的图象上恰有 2 个“等值点”时,m 或8
1 17 m 1 17 .
2 2
【点睛】本题考查了一次函数,反比例函数,二次函数与新定义“等值点”综合运用,一
元二次方程根的判别式,翻折的性质等,解题关键是理解并运用新定义,运用分类讨论
思想解决问题.
试卷第 29页,共 29页
同课章节目录
