第15章轴对称与等腰三角形期末复习(2) 课件(共25张PPT)
文档属性
| 名称 | 第15章轴对称与等腰三角形期末复习(2) 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 863.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 13:45:09 | ||
图片预览




文档简介
(共25张PPT)
第15章 轴对称与 等腰三角形期末复习(2)
等腰三角形与直角三角形
沪科版
1.定义:有两条边_____的三角形叫做等腰三角形.
2.性质:(1)等腰三角形两底角_____ ;
(2)等腰三角形____________ 、底边上的中线、
互相重合,简称三线合一;
(3)等腰三角形是轴对称图形,对称轴是__________
所在的直线.
3.判定:(1)有两条边_____的三角形是等腰三角形;
(2)有_____相等的三角形是等腰三角形.
一.等腰三角形
相等
相等
(等边对等角)
顶角平分线
底边上的高
两角
(等角对等边)
底边上的高
相等
复习要点
1.定义:_______都相等的三角形叫做等边三角形.
2.性质:(1)等边三角形三条边_______ ,三个角_______ ,且每个角都等于_____;
(2)等边三角形是____对称图形,它有____条对称轴.
3.判定:(1)三个边都_____的三角形是等边三角形;
(2)三个角都_____的三角形是等边三角形;
(3)有一个角等于_____的____________是等边三角形.
二.等边三角形
三条边
都相等
都相等
轴
三
相等
相等
60°
等腰三角形
60°
(2)直角三角形中,30°角所对的直角边是斜边_____ .
1.直角三角形的性质
(1)直角三角形的两锐角_____;
互余
一半
三.直角三角形
(2)有两个角_____的三角形是直角三角形.
(1)有一个角是_____的三角形是直角三角形;
直角
互余
2.直角三角形的判定:
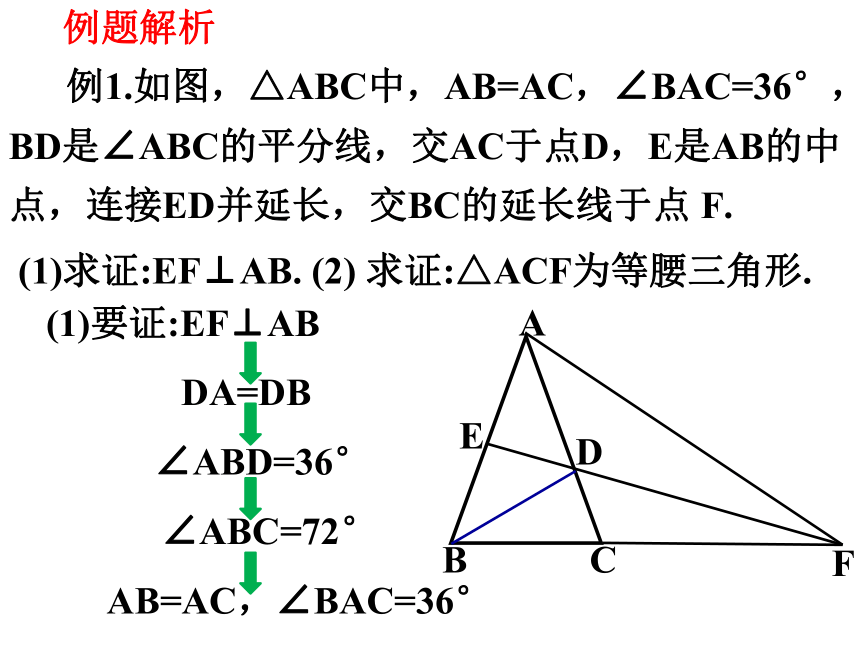
例1.如图,△ABC中,AB=AC,∠BAC=36°, BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点 F.
(1)求证:EF⊥AB. (2) 求证:△ACF为等腰三角形.
例题解析
E
A
B
C
D
F
(1)要证:EF⊥AB
DA=DB
∠ABD=36°
∠ABC=72°
AB=AC,∠BAC=36°
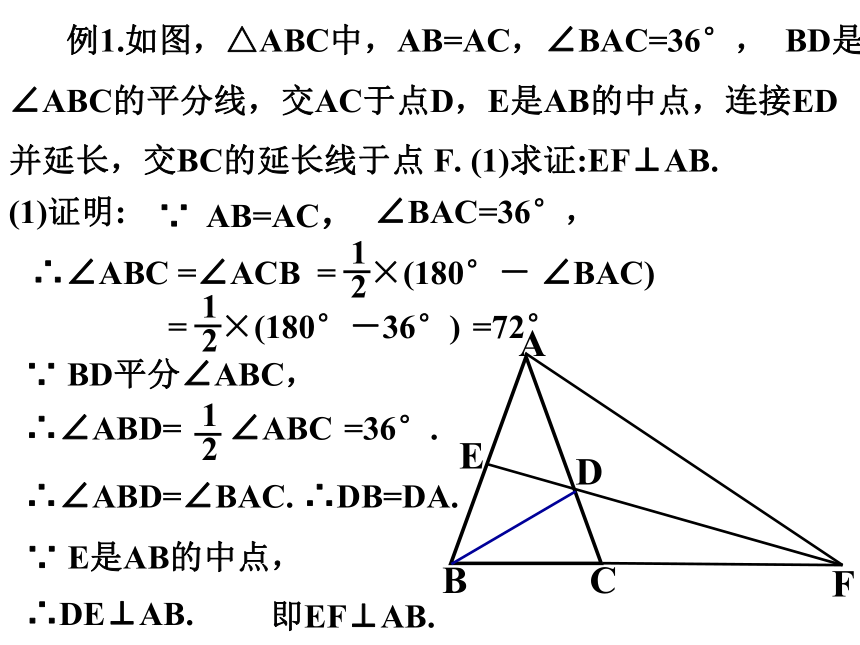
例1.如图,△ABC中,AB=AC,∠BAC=36°, BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点 F. (1)求证:EF⊥AB.
E
A
B
C
D
F
(1)证明:
∵ AB=AC,
∠BAC=36°,
∴∠ABC =∠ACB
=72°
= ×(180°-36°)
∵ BD平分∠ABC,
∴∠ABD=
=36°.
∴∠ABD=∠BAC.
∴DB=DA.
∵ E是AB的中点,
∴DE⊥AB.
即EF⊥AB.
= ×(180°- ∠BAC)
1
2
∠ABC
1
2
1
2
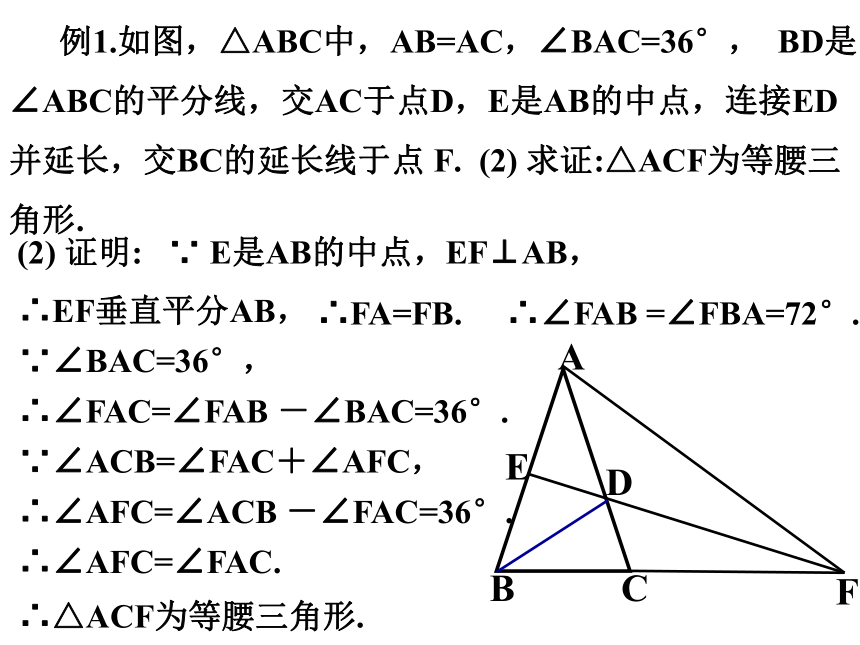
例1.如图,△ABC中,AB=AC,∠BAC=36°, BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点 F. (2) 求证:△ACF为等腰三角形.
E
A
B
C
D
F
(2) 证明:
∵ E是AB的中点,
∴FA=FB.
EF⊥AB,
∴∠FAB =∠FBA=72°.
∵∠BAC=36°,
∴EF垂直平分AB,
∴∠FAC=∠FAB -∠BAC=36°.
∵∠ACB=∠FAC+∠AFC,
∴∠AFC=∠ACB -∠FAC=36°.
∴∠AFC=∠FAC.
∴△ACF为等腰三角形.
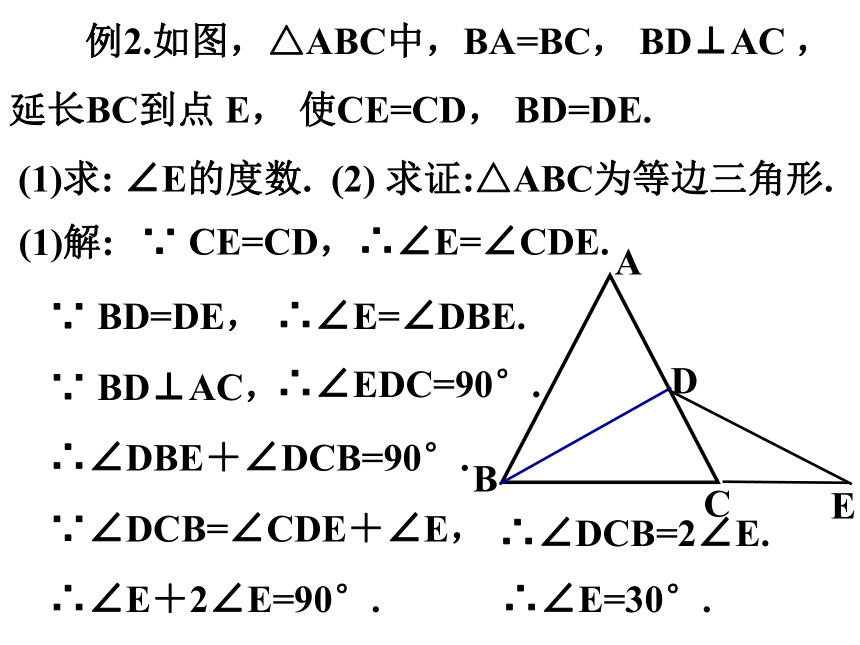
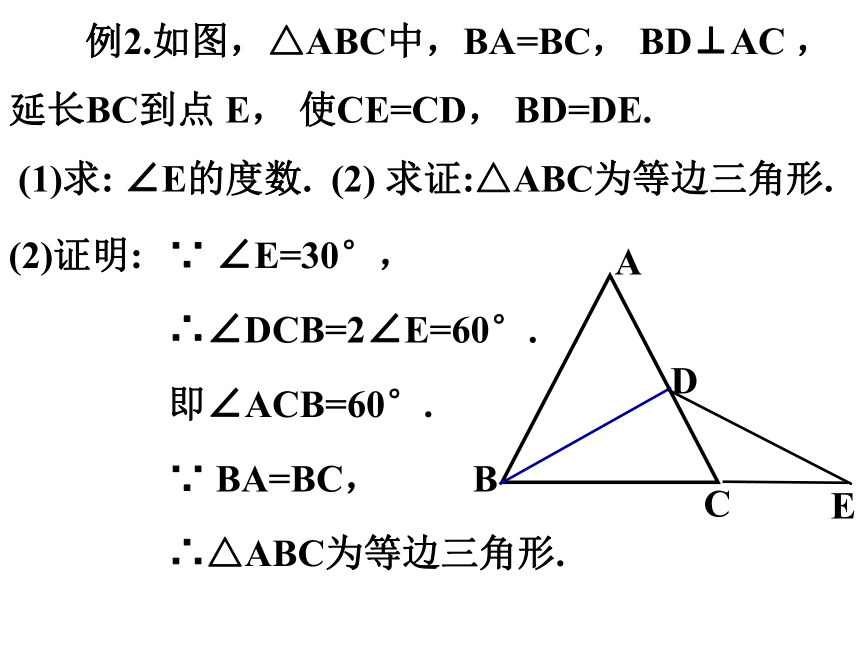
例2.如图,△ABC中,BA=BC, BD⊥AC ,
延长BC到点 E, 使CE=CD, BD=DE.
(1)求: ∠E的度数. (2) 求证:△ABC为等边三角形.
A
B
C
D
E
(1)解:
∵ CE=CD,
∵ BD=DE,
∵ BD⊥AC,
∴∠E=∠CDE.
∴∠E=∠DBE.
∴∠EDC=90°.
∴∠DBE+∠DCB=90°.
∵∠DCB=∠CDE+∠E,
∴∠DCB=2∠E.
∴∠E+2∠E=90°.
∴∠E=30°.
例2.如图,△ABC中,BA=BC, BD⊥AC ,
延长BC到点 E, 使CE=CD, BD=DE.
(1)求: ∠E的度数. (2) 求证:△ABC为等边三角形.
A
B
C
D
E
(2)证明:
∴∠DCB=2∠E=60°.
∵ ∠E=30°,
即∠ACB=60°.
∵ BA=BC,
∴△ABC为等边三角形.
例3.如图,△ABC中,AB=AC,∠BAC=120°,
点D是BC的中点,过点D作DE⊥AB,交AB于
点E,点F是AC的中点,过点作FG⊥AC,交
BC于点G. 求证: = .
ED
CG
3
4
A
B
C
D
E
G
F
证明:
∵ AB=AC,∠BAC=120°,
∴∠B =∠C=30°.
连接AG,
∵ DE⊥AB,
∴∠BED=90°.
∴BD= 2ED.
A
B
C
D
E
G
F
证明:
∵ AB=AC,∠BAC=120°,
∴∠B =∠C=30°.
连接AG,
∵ DE⊥AB,
∴∠BED=90°.
∵点D是BC的中点,
∵点F是AC的中点,
FG⊥AC,
∴AG=CG.
∴FG垂直平分AC,
∴∠GFC=90°,
∠GAC =∠C=30°.
∴∠BAG= ∠BAC-∠GAC =90°,
∴BG=2AG.
∴BG=2CG.
∴BC=BG+CG=3CG.
∴BD=2ED.
∴BC= 2BD.
∴BC=4ED.
∴
ED
CG
=
∴4ED=3CG.
3
4
1.如果等腰三角形两边长是5 cm和3 cm,那么它的周长是( ).
A.8 cm B.11 cm
C.13 cm或11 cm D.13 cm
2.如果等腰三角形两边长是4 cm和9 cm,那么它的周长是( ).
A.13 cm B.17cm
C.17 cm或22 cm D.22 cm
练习巩固
C
D
3. 已知等腰三角形的一个内角为70°,则另两个角的度数是( ).
A.55°,55° B.70°,40°
C.55°,55°或70°,40° D.以上都不对
4. 已知等腰三角形的一个内角为100°,则另两个角的度数是( ).
A.100°,40° B.40°,40°
C.100°,40°或40°,40° D.以上都不对
C
B
5.若等腰三角形的一个角等于42°,则它的
底角为( ).
A.42° B.69°
C.69°或84° D.42°或69°
D
6.若等腰三角形的一个内角等于40°,则
它的这个等腰三角形的最大内角为( ).
A.65° B.40°
C.70°或100° D.65°或100°
C
8.若等腰△ABC的周长为18 cm,BC=8 cm,若△ABC与△A′B′C′全等,则△A′B′C′的腰长等于( ).
A.8 cm B.2 cm或8 cm
C.5 cm D.8 cm或5 cm
C
7.在等腰△ABC中,若∠A=36°,则∠B的
度数不可能为( ).
A.36° B.72° C.108° D.118°
D
9.如图,在△ABC中,AB=AC,点D,E分别在边BC、AC上,AD=AE,若∠BAD=α.则∠1与∠B的关系是( ).
A
B
C
E
D
α
1
A. ∠1-∠B=
B.∠B-∠1 =
C. ∠1+∠B=α
D. ∠1+∠B=2α
α
2
α
2
A
10.如图,在△ABC中, ∠B =41°, ∠C=107°,AD是角平分线,点E是AB上的点,AC=AE,作EF⊥AD,垂足为点F,则∠DEF的度数是( ).
C
A.16° B.32°
C.33° D.34°
A
B
C
E
D
F
11.在△ABC中,AB=AC, ∠B =75°,
则∠A的度数为 .
12.如图,△ABC中,AC=BC,∠B=20°,
点D是AC的中点,过点D作DE⊥AC,交BC的
延长线于点E,连接AE,则∠EAB = 度.
A
B
C
D
E
30°
60
13.如图,在△ABC中,AB =AC, 点D是△ABC 的三条角平分线的交点,若∠1=125°,则∠ABC的度数是 .
A
B
C
D
1
14.如图, △ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD, DF=DE,则∠E的度数为 .
A
B
C
D
E
F
G
70°
15°
15.已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′、EB′分别交边AC于点F、G,若∠ADF=80°,则∠EGC的度数为______.
B
A
C
E
D
B′
F
G
80°
17.如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,AD=2cm,则BC= cm.
A
B
C
D
16.如图,在Rt△ABC中,∠ACB=90°, ∠B=30°,AD=2cm,CD是Rt△ABC的高,则BD= cm.
A
B
C
D
6
6
18.如图,等边△ABC的边长为8,点D是AB的中点,过点D作DF⊥AC于点F,过点F作FE⊥BC于点E,则线段BE的长为____.
A
B
C
D
E
F
5
19.如图,在△ABC中,AB =AC, DE∥BC,点F是BC 的中点,连接FD,FE. 求证:FD=FE.
A
B
C
D
E
F
证明:
∵ AB=AC ,
∴∠ B=∠C,
∵DE∥BC,
∴∠ADE=∠B,
∠AED=∠C,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F是BC 的中点,
∴BF=CF,
∴ △BDF≌△CEF
(SAS).
∴FD=FE.
20.如图,点D在等边△ABC的边AC上, 点E在AB的延长线上,使BE =CD,DE交BC于点P.求证:PD=PE.
C
A
B
D
E
P
证明:
过点D作DF∥AB,交BC于点F,
∵ △ABC是等边三角形,
∴∠CDF =∠A,
∠CFD =∠CBA,
∴∠A =∠CBA=∠C=60°.
∴∠CDF =∠CFD=60°.
∴△CDF是等边三角形,
∴CD =FD.
∵ BE =CD,
∴BE =FD.
∠FDE =∠E.
∵∠DPF =∠EPB,
∴△BPE≌△FPD
(AAS).
∴PD=PE.
F
21.如图,在Rt △ABC中,AC=BC, ∠ACB=90°, 点D是BC延长线上一点, 连接AD,作BE⊥AD于点E,
且交AC于点F,连接FD,作FG⊥FD,交BC于点G.
求证:FG∥AB.
A
B
C
D
E
F
G
证明:
∵ AC=BC, ∠ACB=90°,
∠ACD =90°.
∴∠ABC =45°,
∴∠DAC+∠ADC=90°.
∵ BE⊥AD,
∴∠BED =90°.
∴∠EBD+∠ADC=90°.
∴∠DAC =∠EBD.
∴△BCF≌△ACD
(ASA).
∴CD=CF .
∴∠C FD=45°.
∵ FG⊥FD,
∴∠GFD =90°.
∴∠C FG=45°.
∴∠CGF=45°.
∴∠ABC =∠CGF.
∴FG∥AB.
第15章 轴对称与 等腰三角形期末复习(2)
等腰三角形与直角三角形
沪科版
1.定义:有两条边_____的三角形叫做等腰三角形.
2.性质:(1)等腰三角形两底角_____ ;
(2)等腰三角形____________ 、底边上的中线、
互相重合,简称三线合一;
(3)等腰三角形是轴对称图形,对称轴是__________
所在的直线.
3.判定:(1)有两条边_____的三角形是等腰三角形;
(2)有_____相等的三角形是等腰三角形.
一.等腰三角形
相等
相等
(等边对等角)
顶角平分线
底边上的高
两角
(等角对等边)
底边上的高
相等
复习要点
1.定义:_______都相等的三角形叫做等边三角形.
2.性质:(1)等边三角形三条边_______ ,三个角_______ ,且每个角都等于_____;
(2)等边三角形是____对称图形,它有____条对称轴.
3.判定:(1)三个边都_____的三角形是等边三角形;
(2)三个角都_____的三角形是等边三角形;
(3)有一个角等于_____的____________是等边三角形.
二.等边三角形
三条边
都相等
都相等
轴
三
相等
相等
60°
等腰三角形
60°
(2)直角三角形中,30°角所对的直角边是斜边_____ .
1.直角三角形的性质
(1)直角三角形的两锐角_____;
互余
一半
三.直角三角形
(2)有两个角_____的三角形是直角三角形.
(1)有一个角是_____的三角形是直角三角形;
直角
互余
2.直角三角形的判定:
例1.如图,△ABC中,AB=AC,∠BAC=36°, BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点 F.
(1)求证:EF⊥AB. (2) 求证:△ACF为等腰三角形.
例题解析
E
A
B
C
D
F
(1)要证:EF⊥AB
DA=DB
∠ABD=36°
∠ABC=72°
AB=AC,∠BAC=36°
例1.如图,△ABC中,AB=AC,∠BAC=36°, BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点 F. (1)求证:EF⊥AB.
E
A
B
C
D
F
(1)证明:
∵ AB=AC,
∠BAC=36°,
∴∠ABC =∠ACB
=72°
= ×(180°-36°)
∵ BD平分∠ABC,
∴∠ABD=
=36°.
∴∠ABD=∠BAC.
∴DB=DA.
∵ E是AB的中点,
∴DE⊥AB.
即EF⊥AB.
= ×(180°- ∠BAC)
1
2
∠ABC
1
2
1
2
例1.如图,△ABC中,AB=AC,∠BAC=36°, BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点 F. (2) 求证:△ACF为等腰三角形.
E
A
B
C
D
F
(2) 证明:
∵ E是AB的中点,
∴FA=FB.
EF⊥AB,
∴∠FAB =∠FBA=72°.
∵∠BAC=36°,
∴EF垂直平分AB,
∴∠FAC=∠FAB -∠BAC=36°.
∵∠ACB=∠FAC+∠AFC,
∴∠AFC=∠ACB -∠FAC=36°.
∴∠AFC=∠FAC.
∴△ACF为等腰三角形.
例2.如图,△ABC中,BA=BC, BD⊥AC ,
延长BC到点 E, 使CE=CD, BD=DE.
(1)求: ∠E的度数. (2) 求证:△ABC为等边三角形.
A
B
C
D
E
(1)解:
∵ CE=CD,
∵ BD=DE,
∵ BD⊥AC,
∴∠E=∠CDE.
∴∠E=∠DBE.
∴∠EDC=90°.
∴∠DBE+∠DCB=90°.
∵∠DCB=∠CDE+∠E,
∴∠DCB=2∠E.
∴∠E+2∠E=90°.
∴∠E=30°.
例2.如图,△ABC中,BA=BC, BD⊥AC ,
延长BC到点 E, 使CE=CD, BD=DE.
(1)求: ∠E的度数. (2) 求证:△ABC为等边三角形.
A
B
C
D
E
(2)证明:
∴∠DCB=2∠E=60°.
∵ ∠E=30°,
即∠ACB=60°.
∵ BA=BC,
∴△ABC为等边三角形.
例3.如图,△ABC中,AB=AC,∠BAC=120°,
点D是BC的中点,过点D作DE⊥AB,交AB于
点E,点F是AC的中点,过点作FG⊥AC,交
BC于点G. 求证: = .
ED
CG
3
4
A
B
C
D
E
G
F
证明:
∵ AB=AC,∠BAC=120°,
∴∠B =∠C=30°.
连接AG,
∵ DE⊥AB,
∴∠BED=90°.
∴BD= 2ED.
A
B
C
D
E
G
F
证明:
∵ AB=AC,∠BAC=120°,
∴∠B =∠C=30°.
连接AG,
∵ DE⊥AB,
∴∠BED=90°.
∵点D是BC的中点,
∵点F是AC的中点,
FG⊥AC,
∴AG=CG.
∴FG垂直平分AC,
∴∠GFC=90°,
∠GAC =∠C=30°.
∴∠BAG= ∠BAC-∠GAC =90°,
∴BG=2AG.
∴BG=2CG.
∴BC=BG+CG=3CG.
∴BD=2ED.
∴BC= 2BD.
∴BC=4ED.
∴
ED
CG
=
∴4ED=3CG.
3
4
1.如果等腰三角形两边长是5 cm和3 cm,那么它的周长是( ).
A.8 cm B.11 cm
C.13 cm或11 cm D.13 cm
2.如果等腰三角形两边长是4 cm和9 cm,那么它的周长是( ).
A.13 cm B.17cm
C.17 cm或22 cm D.22 cm
练习巩固
C
D
3. 已知等腰三角形的一个内角为70°,则另两个角的度数是( ).
A.55°,55° B.70°,40°
C.55°,55°或70°,40° D.以上都不对
4. 已知等腰三角形的一个内角为100°,则另两个角的度数是( ).
A.100°,40° B.40°,40°
C.100°,40°或40°,40° D.以上都不对
C
B
5.若等腰三角形的一个角等于42°,则它的
底角为( ).
A.42° B.69°
C.69°或84° D.42°或69°
D
6.若等腰三角形的一个内角等于40°,则
它的这个等腰三角形的最大内角为( ).
A.65° B.40°
C.70°或100° D.65°或100°
C
8.若等腰△ABC的周长为18 cm,BC=8 cm,若△ABC与△A′B′C′全等,则△A′B′C′的腰长等于( ).
A.8 cm B.2 cm或8 cm
C.5 cm D.8 cm或5 cm
C
7.在等腰△ABC中,若∠A=36°,则∠B的
度数不可能为( ).
A.36° B.72° C.108° D.118°
D
9.如图,在△ABC中,AB=AC,点D,E分别在边BC、AC上,AD=AE,若∠BAD=α.则∠1与∠B的关系是( ).
A
B
C
E
D
α
1
A. ∠1-∠B=
B.∠B-∠1 =
C. ∠1+∠B=α
D. ∠1+∠B=2α
α
2
α
2
A
10.如图,在△ABC中, ∠B =41°, ∠C=107°,AD是角平分线,点E是AB上的点,AC=AE,作EF⊥AD,垂足为点F,则∠DEF的度数是( ).
C
A.16° B.32°
C.33° D.34°
A
B
C
E
D
F
11.在△ABC中,AB=AC, ∠B =75°,
则∠A的度数为 .
12.如图,△ABC中,AC=BC,∠B=20°,
点D是AC的中点,过点D作DE⊥AC,交BC的
延长线于点E,连接AE,则∠EAB = 度.
A
B
C
D
E
30°
60
13.如图,在△ABC中,AB =AC, 点D是△ABC 的三条角平分线的交点,若∠1=125°,则∠ABC的度数是 .
A
B
C
D
1
14.如图, △ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD, DF=DE,则∠E的度数为 .
A
B
C
D
E
F
G
70°
15°
15.已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′、EB′分别交边AC于点F、G,若∠ADF=80°,则∠EGC的度数为______.
B
A
C
E
D
B′
F
G
80°
17.如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,AD=2cm,则BC= cm.
A
B
C
D
16.如图,在Rt△ABC中,∠ACB=90°, ∠B=30°,AD=2cm,CD是Rt△ABC的高,则BD= cm.
A
B
C
D
6
6
18.如图,等边△ABC的边长为8,点D是AB的中点,过点D作DF⊥AC于点F,过点F作FE⊥BC于点E,则线段BE的长为____.
A
B
C
D
E
F
5
19.如图,在△ABC中,AB =AC, DE∥BC,点F是BC 的中点,连接FD,FE. 求证:FD=FE.
A
B
C
D
E
F
证明:
∵ AB=AC ,
∴∠ B=∠C,
∵DE∥BC,
∴∠ADE=∠B,
∠AED=∠C,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F是BC 的中点,
∴BF=CF,
∴ △BDF≌△CEF
(SAS).
∴FD=FE.
20.如图,点D在等边△ABC的边AC上, 点E在AB的延长线上,使BE =CD,DE交BC于点P.求证:PD=PE.
C
A
B
D
E
P
证明:
过点D作DF∥AB,交BC于点F,
∵ △ABC是等边三角形,
∴∠CDF =∠A,
∠CFD =∠CBA,
∴∠A =∠CBA=∠C=60°.
∴∠CDF =∠CFD=60°.
∴△CDF是等边三角形,
∴CD =FD.
∵ BE =CD,
∴BE =FD.
∠FDE =∠E.
∵∠DPF =∠EPB,
∴△BPE≌△FPD
(AAS).
∴PD=PE.
F
21.如图,在Rt △ABC中,AC=BC, ∠ACB=90°, 点D是BC延长线上一点, 连接AD,作BE⊥AD于点E,
且交AC于点F,连接FD,作FG⊥FD,交BC于点G.
求证:FG∥AB.
A
B
C
D
E
F
G
证明:
∵ AC=BC, ∠ACB=90°,
∠ACD =90°.
∴∠ABC =45°,
∴∠DAC+∠ADC=90°.
∵ BE⊥AD,
∴∠BED =90°.
∴∠EBD+∠ADC=90°.
∴∠DAC =∠EBD.
∴△BCF≌△ACD
(ASA).
∴CD=CF .
∴∠C FD=45°.
∵ FG⊥FD,
∴∠GFD =90°.
∴∠C FG=45°.
∴∠CGF=45°.
∴∠ABC =∠CGF.
∴FG∥AB.
