第13章命题与证明期末复习 课件(共25张PPT)
文档属性
| 名称 | 第13章命题与证明期末复习 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 406.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第13章命题与证明期末复习
能界定某个对象含义的句子叫做定义.
复习要点
1.定义
对某一件事情作出正确或不正确判断的句子叫命题.
3.命题的结构
数学命题通常是由题设和结论两部分组成.
2.命题
常可写成 “如果 ……,那么……” 的形式.
5.判断一个命题的真假
要判断一个命题是真命题需要推理论证;要判断一个命题是假命题只要举出一个反例即可.
正确的命题叫真命题.
错误的命题叫假命题.
4.真命题与假命题
把一个命题的题设和结论互换,便可以得到一个新的命题,我们称这样的两个命题为互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
6.互逆命题
从已知条件出发,根据定义、基本事实、已证定理,并根据逻辑规则,推导出结论的方法叫“演绎推理”.演绎推理的过程,叫做演绎证明,简称证明.
7.证明
从基本事实或其他真命题出发,用推理方法证明为正确的、并进一步作为判断其他命题真假的依据,这样的真命题叫做定理.
8.定理
9.命题的证明一般步骤:
(1)分清命题的题设和结论,根据题意,画出图形;
(2)结合图形,将命题的题设和结论,写成已知、
求证的形式;
(3)分析思考,寻找由题设推出结论的途径,写
出证明过程.
例1.先把命题“绝对值等于3的数是3”改写成“如果p,那么q”的形式,再写出这个命题的逆命题,然后判断原命题与逆命题的真假.
例题解析
命题“绝对值等于3的数是3”改写成“如果p,那么q”的形式为:
如果一个数绝对值等于3,那么这个数是3.
这个命题的逆命题为
数3的绝对值等于3.
原命题假命题,
它逆命题的是真命题.
解:
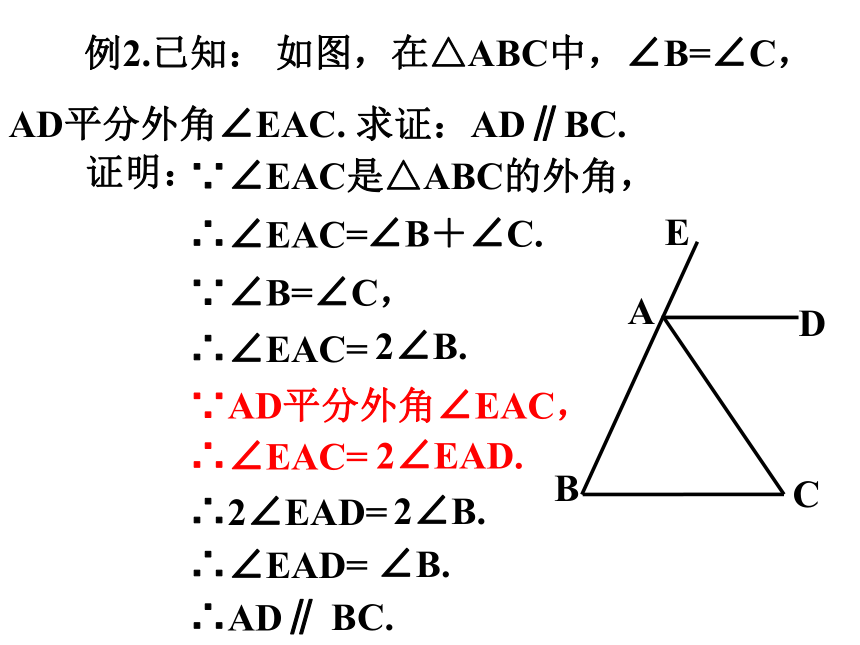
例2.已知: 如图,在△ABC中,∠B=∠C,AD平分外角∠EAC. 求证:AD∥BC.
A
B
C
E
D
证明:
∵∠EAC是△ABC的外角,
∴∠EAC=
∠B+∠C.
∵∠B=∠C,
∴∠EAC=
2∠B.
∵AD平分外角∠EAC,
∴∠EAC=
2∠EAD.
∴2∠EAD=
2∠B.
∴∠EAD=
∠B.
∴AD∥
BC.
1.下列语句属于命题的是( ).
A.对顶角都相等吗? B.画线段AB.
C.作∠A的平分线. D.内错角不相等.
D
练习巩固
B.两条直线相交,有且只有一个交点.
D.一个平角的度数是180度.
A.长度相等的两条线段是相等的线段吗?
C.不相等的两个角不是对顶角.
2.下列语句是不是命题的是( ).
A
3.下列命题中,是真命题的是( ).
A. 一个数能被6整除,这个数也能被4整除.
B.三角形三条高所在直线一定相交于三角形内.
C. 两直线平行,同旁内角互补.
D. 三角形的三个外角和等于180°.
C
4.下列命题中,是假命题的是( ).
A. 两直线平行,同位角相等;
B.若a=-b,则|a|=|b|;
C.若ab>0,则a>0,b>0;
D.两条直线被第三条直线所截,如果
同旁内角互补,那么这两条直线平行.
C
5.能说明命题“若为a实数,则a2>0”为
假命题的反例是( ).
A.a=2 B.a=-1
C.a=-0.5 D.a=0
D
6.下列命题中,它的逆命题是假命题的是( ).
A. 两直线平行,同位角相等..
B.若|a|+|b|=0,则a=0,b=0;
C.若a>0,b>0,则ab>0;
D.直角三角形两个锐角互余.
C
7.下列命题中,它的逆命题是真命题的是( ).
A.如果a3=b3,那么a=b.
B.如果a=2,那么a2=4.
C.如果a>0,那么a2>0.
D.如果a=0,那么ab=0.
A
8.下列命题:
①对顶角相等;
②同位角相等,两直线平行;
③若a=b,则|a|=|b|;
④若a=0,则ab=0
它们的逆命题一定成立的有( )
A.①②③④ B.①④ C.②④ D.②
D
9.下列命题:
①两条直线被第三条直线所截,同位角相等;
②两点之间,线段最短;
③相等的角是对顶角;
④两个锐角的和是锐角;
⑤同角或等角的补角相等.
其中正确命题的个数是( ).
A.2个 B.3个 C.4个 D.5个
A
10.下列命题可作为定理的有( ).
①相等的角是对顶角.
②同旁内角互补,两直线平行.
③同角或等角的补角相等.
④垂线段最短.
A.①②③④ B.①②④
C. ②③④ D.②③
C
11.如图,下列推理错误的是( ).
A. ∵∠1=∠5 , ∴AB∥CD
B. ∵AD∥BC, ∴∠2=∠6
C. ∵∠4=∠8 , ∴AB∥CD
D. ∵AD∥BC , ∴ ∠5=∠7
2
3
1
4
A
B
D
6
C
5
7
8
D
12.如图,下列推理及其依据均正确的是( ).
A.∵∠1=∠B ,∴AD∥BC
B.∵∠2=∠C, ∴AD∥BC
C.∵∠DAB+∠B =180° ,
∴AD∥BC
D. ∵∠2+∠B =180° ,
∴ AD∥BC .
C
(两直线平行,内错角相等)
(两直线平行,同位角相等)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
A
B
C
E
D
1
2
13.命题“同位角相等,两直线平行”的题设
是 ,结论是 .
同位角相等
两直线平行
14.命题“直角三角形两个锐角互余”的逆命题
是 .
两个锐角互余的三角形是直角三角形
16.将命题“互为相反数的两个数的和为零”
改写成“如果……,那么……”的形式:
.这个命题是 命题. ( 填“真”或“假” )
如果两个数是互为相反数,
那么这两个数的和为零.
真
15.命题“如果a+b=0,那么a=0,b=0”的
逆命题是 .
如果a=0,b=0,那么a+b=0
请你选择其中两个条件为题设,另外一个条件为结论,构造一个命题.在构成的所有命题中,正确的命题有 个.
9.如图(3),现给出如下三个条件:①
17.如图,现给出如下三个条件:
②AD=AE;
③ ∠ B= ∠ C.
①AB =AC;
A
B
C
D
E
三
18.命题“任意一个实数都等于0.”
证明:设任意一个实数为x,令x=m,
等式两边都乘以x,得x2=xm.①
等式两边都减m2,得x2-m2=xm-m2 ②
等式两边分别分解因式,得
(x+m)(x-m)=x(x-m).③
等式两边都除以(x-m),得 x+m=m.④
等式两边都减m,得x=0.⑤
∴任意一个实数都等于0.
以上推理过程中,开始出现错误的那一步是 .
④
( )
( )
已知,如图,AB⊥BF, CD⊥BF,
∠1=∠2 . 求证: ∠3=∠4.
证明:∵ AB⊥BF,CD⊥BF
∴∠B=∠CDF=90°
∴AB//CD.
又∵∠1=∠2,
∴AB//EF.
∴CD//EF.
∴∠3=∠4.
已知
垂直定义
同位角相等,两直线平行
(已知)
( )
平行于同一直线的两直线平行
两直线平行,同位角相等
( )
( )
( )
内错角相等,两直线平行
1
2
3
4
A
B
C
D
E
F
2.
19.填写下列证明过程的推理依据
请你选择其中两个条件为题设,另外一个条件为结论,构造一个真命题.写出这个真命题,并给予证明.
9.如图(3),现给出如下三个条件:①
20.如图,现给出如下三个条件:
② ∠B=∠C ;
③ ∠E=∠F.
①AB // AC;
条件: ,
结论: .(填序号)
①
②
③
A
B
C
D
E
F
9.如图(3),现给出如下三个条件:①
20.如图,现给出如下三个条件:
② ∠B=∠C ;
③ ∠E=∠F.
①AB // AC;
条件: ,
结论: .(填序号)
①
②
③
A
B
C
D
E
F
∵ AB // AC,
∴∠EAB=∠C .
∵ ∠B=∠C ,
证明:
∴∠EAB=∠B .
∴ AB // AC,
∴∠E=∠F.
第13章命题与证明期末复习
能界定某个对象含义的句子叫做定义.
复习要点
1.定义
对某一件事情作出正确或不正确判断的句子叫命题.
3.命题的结构
数学命题通常是由题设和结论两部分组成.
2.命题
常可写成 “如果 ……,那么……” 的形式.
5.判断一个命题的真假
要判断一个命题是真命题需要推理论证;要判断一个命题是假命题只要举出一个反例即可.
正确的命题叫真命题.
错误的命题叫假命题.
4.真命题与假命题
把一个命题的题设和结论互换,便可以得到一个新的命题,我们称这样的两个命题为互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
6.互逆命题
从已知条件出发,根据定义、基本事实、已证定理,并根据逻辑规则,推导出结论的方法叫“演绎推理”.演绎推理的过程,叫做演绎证明,简称证明.
7.证明
从基本事实或其他真命题出发,用推理方法证明为正确的、并进一步作为判断其他命题真假的依据,这样的真命题叫做定理.
8.定理
9.命题的证明一般步骤:
(1)分清命题的题设和结论,根据题意,画出图形;
(2)结合图形,将命题的题设和结论,写成已知、
求证的形式;
(3)分析思考,寻找由题设推出结论的途径,写
出证明过程.
例1.先把命题“绝对值等于3的数是3”改写成“如果p,那么q”的形式,再写出这个命题的逆命题,然后判断原命题与逆命题的真假.
例题解析
命题“绝对值等于3的数是3”改写成“如果p,那么q”的形式为:
如果一个数绝对值等于3,那么这个数是3.
这个命题的逆命题为
数3的绝对值等于3.
原命题假命题,
它逆命题的是真命题.
解:
例2.已知: 如图,在△ABC中,∠B=∠C,AD平分外角∠EAC. 求证:AD∥BC.
A
B
C
E
D
证明:
∵∠EAC是△ABC的外角,
∴∠EAC=
∠B+∠C.
∵∠B=∠C,
∴∠EAC=
2∠B.
∵AD平分外角∠EAC,
∴∠EAC=
2∠EAD.
∴2∠EAD=
2∠B.
∴∠EAD=
∠B.
∴AD∥
BC.
1.下列语句属于命题的是( ).
A.对顶角都相等吗? B.画线段AB.
C.作∠A的平分线. D.内错角不相等.
D
练习巩固
B.两条直线相交,有且只有一个交点.
D.一个平角的度数是180度.
A.长度相等的两条线段是相等的线段吗?
C.不相等的两个角不是对顶角.
2.下列语句是不是命题的是( ).
A
3.下列命题中,是真命题的是( ).
A. 一个数能被6整除,这个数也能被4整除.
B.三角形三条高所在直线一定相交于三角形内.
C. 两直线平行,同旁内角互补.
D. 三角形的三个外角和等于180°.
C
4.下列命题中,是假命题的是( ).
A. 两直线平行,同位角相等;
B.若a=-b,则|a|=|b|;
C.若ab>0,则a>0,b>0;
D.两条直线被第三条直线所截,如果
同旁内角互补,那么这两条直线平行.
C
5.能说明命题“若为a实数,则a2>0”为
假命题的反例是( ).
A.a=2 B.a=-1
C.a=-0.5 D.a=0
D
6.下列命题中,它的逆命题是假命题的是( ).
A. 两直线平行,同位角相等..
B.若|a|+|b|=0,则a=0,b=0;
C.若a>0,b>0,则ab>0;
D.直角三角形两个锐角互余.
C
7.下列命题中,它的逆命题是真命题的是( ).
A.如果a3=b3,那么a=b.
B.如果a=2,那么a2=4.
C.如果a>0,那么a2>0.
D.如果a=0,那么ab=0.
A
8.下列命题:
①对顶角相等;
②同位角相等,两直线平行;
③若a=b,则|a|=|b|;
④若a=0,则ab=0
它们的逆命题一定成立的有( )
A.①②③④ B.①④ C.②④ D.②
D
9.下列命题:
①两条直线被第三条直线所截,同位角相等;
②两点之间,线段最短;
③相等的角是对顶角;
④两个锐角的和是锐角;
⑤同角或等角的补角相等.
其中正确命题的个数是( ).
A.2个 B.3个 C.4个 D.5个
A
10.下列命题可作为定理的有( ).
①相等的角是对顶角.
②同旁内角互补,两直线平行.
③同角或等角的补角相等.
④垂线段最短.
A.①②③④ B.①②④
C. ②③④ D.②③
C
11.如图,下列推理错误的是( ).
A. ∵∠1=∠5 , ∴AB∥CD
B. ∵AD∥BC, ∴∠2=∠6
C. ∵∠4=∠8 , ∴AB∥CD
D. ∵AD∥BC , ∴ ∠5=∠7
2
3
1
4
A
B
D
6
C
5
7
8
D
12.如图,下列推理及其依据均正确的是( ).
A.∵∠1=∠B ,∴AD∥BC
B.∵∠2=∠C, ∴AD∥BC
C.∵∠DAB+∠B =180° ,
∴AD∥BC
D. ∵∠2+∠B =180° ,
∴ AD∥BC .
C
(两直线平行,内错角相等)
(两直线平行,同位角相等)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
A
B
C
E
D
1
2
13.命题“同位角相等,两直线平行”的题设
是 ,结论是 .
同位角相等
两直线平行
14.命题“直角三角形两个锐角互余”的逆命题
是 .
两个锐角互余的三角形是直角三角形
16.将命题“互为相反数的两个数的和为零”
改写成“如果……,那么……”的形式:
.这个命题是 命题. ( 填“真”或“假” )
如果两个数是互为相反数,
那么这两个数的和为零.
真
15.命题“如果a+b=0,那么a=0,b=0”的
逆命题是 .
如果a=0,b=0,那么a+b=0
请你选择其中两个条件为题设,另外一个条件为结论,构造一个命题.在构成的所有命题中,正确的命题有 个.
9.如图(3),现给出如下三个条件:①
17.如图,现给出如下三个条件:
②AD=AE;
③ ∠ B= ∠ C.
①AB =AC;
A
B
C
D
E
三
18.命题“任意一个实数都等于0.”
证明:设任意一个实数为x,令x=m,
等式两边都乘以x,得x2=xm.①
等式两边都减m2,得x2-m2=xm-m2 ②
等式两边分别分解因式,得
(x+m)(x-m)=x(x-m).③
等式两边都除以(x-m),得 x+m=m.④
等式两边都减m,得x=0.⑤
∴任意一个实数都等于0.
以上推理过程中,开始出现错误的那一步是 .
④
( )
( )
已知,如图,AB⊥BF, CD⊥BF,
∠1=∠2 . 求证: ∠3=∠4.
证明:∵ AB⊥BF,CD⊥BF
∴∠B=∠CDF=90°
∴AB//CD.
又∵∠1=∠2,
∴AB//EF.
∴CD//EF.
∴∠3=∠4.
已知
垂直定义
同位角相等,两直线平行
(已知)
( )
平行于同一直线的两直线平行
两直线平行,同位角相等
( )
( )
( )
内错角相等,两直线平行
1
2
3
4
A
B
C
D
E
F
2.
19.填写下列证明过程的推理依据
请你选择其中两个条件为题设,另外一个条件为结论,构造一个真命题.写出这个真命题,并给予证明.
9.如图(3),现给出如下三个条件:①
20.如图,现给出如下三个条件:
② ∠B=∠C ;
③ ∠E=∠F.
①AB // AC;
条件: ,
结论: .(填序号)
①
②
③
A
B
C
D
E
F
9.如图(3),现给出如下三个条件:①
20.如图,现给出如下三个条件:
② ∠B=∠C ;
③ ∠E=∠F.
①AB // AC;
条件: ,
结论: .(填序号)
①
②
③
A
B
C
D
E
F
∵ AB // AC,
∴∠EAB=∠C .
∵ ∠B=∠C ,
证明:
∴∠EAB=∠B .
∴ AB // AC,
∴∠E=∠F.
