第14章 全等三角形期末复习 课件(共26张PPT)
文档属性
| 名称 | 第14章 全等三角形期末复习 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 15:44:04 | ||
图片预览




文档简介
(共26张PPT)
第14章 全等三角形的判定
全等三角形的对应边上的高相等.
全等三角形的对应边上的中线相等.
全等三角形的对应角的平分线相等.
全等三角形的对应边相等.
全等三角形的对应角相等.
2.全等三角形的性质:
复习要点
能够完全重合的两个三角形称为全等三角形.
1.全等三角形的定义
3.全等三角形的判定方法
一般三角形:
SSS
SAS
ASA
AAS
直角三角形:
HL
SAS
ASA
AAS
判定两个三角形全等的条件中
至少有一组边对应相等.
结论:
复习要点
复习要点
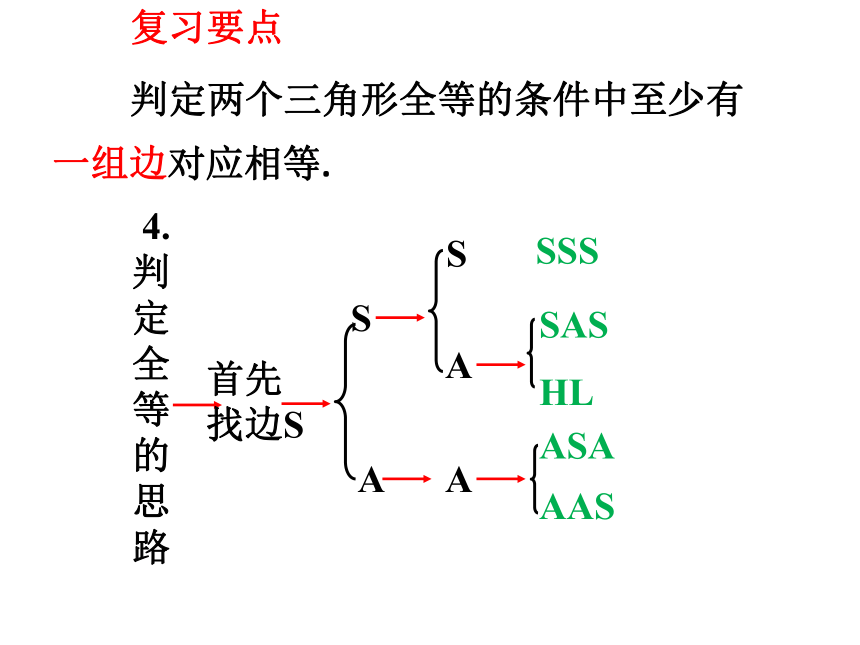
4.
判
定
全
等
的
思
路
首先
找边S
S
S
A
SAS
A
A
ASA
AAS
SSS
HL
判定两个三角形全等的条件中至少有
一组边对应相等.
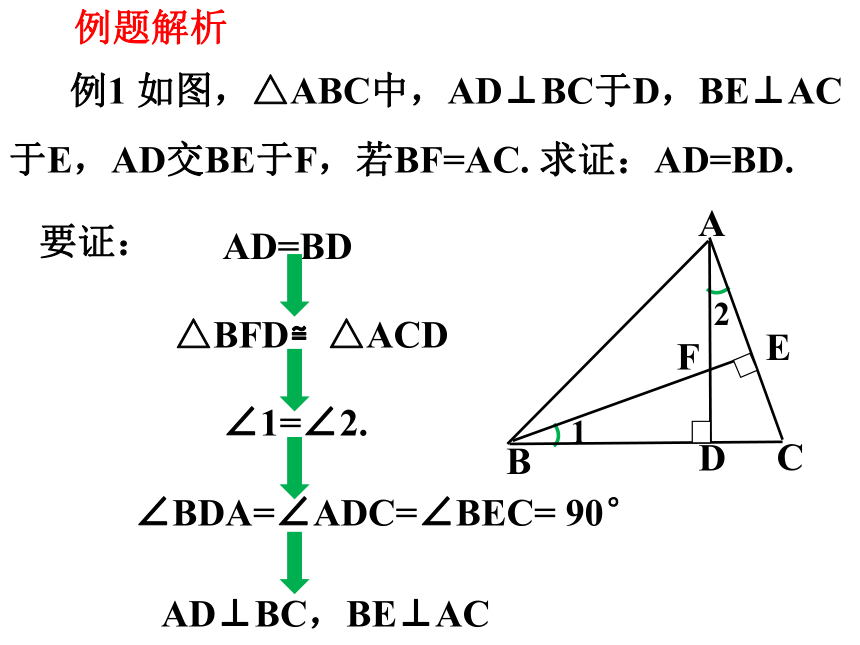
例1 如图,△ABC中,AD⊥BC于D,BE⊥AC
于E,AD交BE于F,若BF=AC. 求证:AD=BD.
AD⊥BC,BE⊥AC
△BFD≌△ACD
AD=BD
∠1=∠2.
∠BDA=∠ADC=∠BEC= 90°
要证:
例题解析
1
2
A
B
C
D
F
E
∵AD⊥BC,BE⊥AC,
∴△BFD≌△ACD
∴ AD=BD.
∴ ∠1=∠2.
BF=AC
∠2 + ∠C= 90°,
∴ ∠1 + ∠C= 90°,
∴∠BDA=∠ADC=∠BEC= 90°
在△BFD和△ACD中,
∠BDF=∠ADC
∠1=∠2
证明:
(AAS)
1
2
A
B
C
D
F
E
例1 如图,△ABC中,AD⊥BC于D,BE⊥AC
于E,AD交BE于F,若BF=AC. 求证:AD=BD.
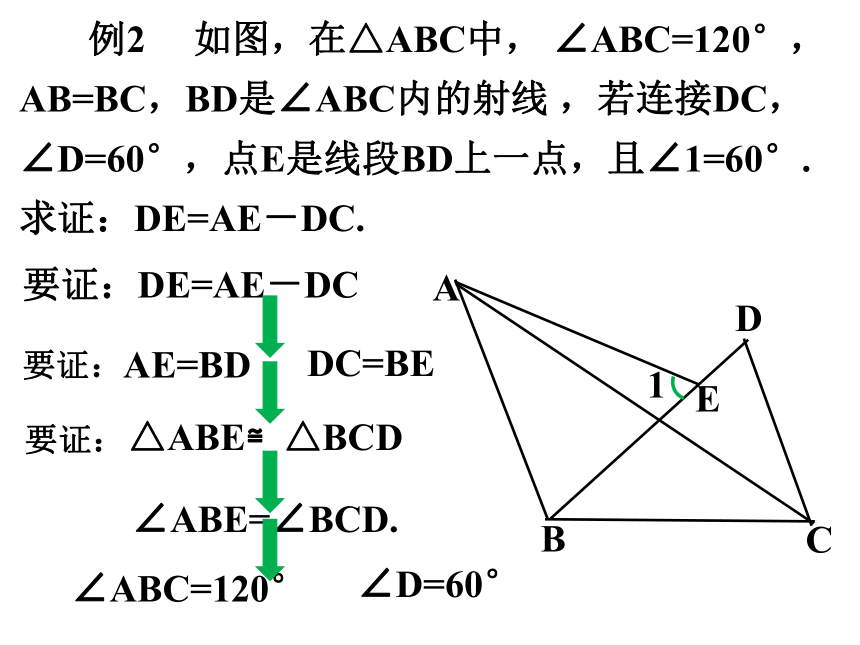
例2 如图,在△ABC中, ∠ABC=120°, AB=BC,BD是∠ABC内的射线 ,若连接DC, ∠D=60°,点E是线段BD上一点,且∠1=60°. 求证:DE=AE-DC.
A
B
C
D
E
1
要证:DE=AE-DC
AE=BD
DC=BE
要证:
要证:
△ABE≌△BCD
∠ABE=∠BCD.
∠ABC=120°
∠D=60°
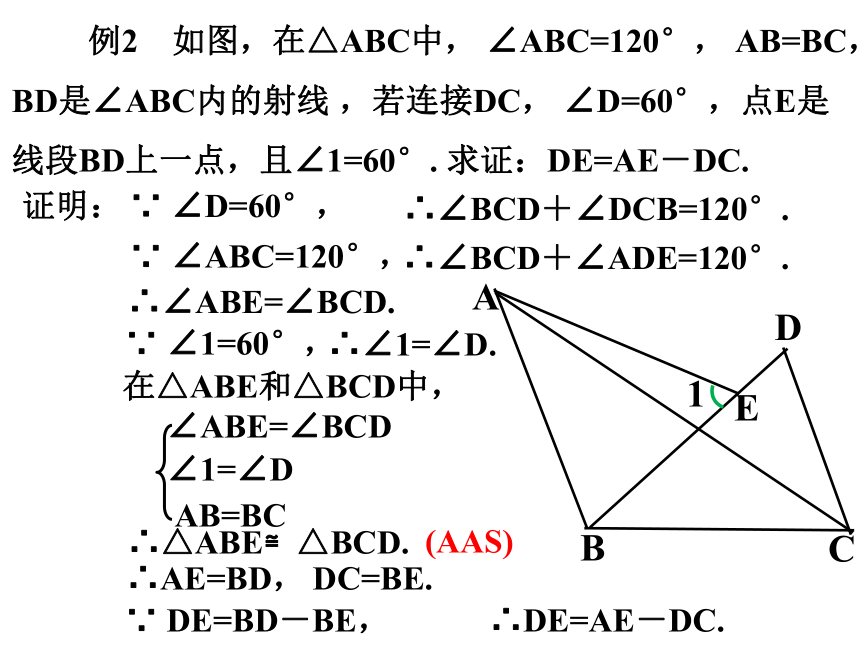
例2 如图,在△ABC中, ∠ABC=120°, AB=BC,BD是∠ABC内的射线 ,若连接DC, ∠D=60°,点E是线段BD上一点,且∠1=60°. 求证:DE=AE-DC.
A
B
C
D
E
1
∴DE=AE-DC.
∴AE=BD,
DC=BE.
∴△ABE≌△BCD.
∴∠ABE=∠BCD.
∵ ∠ABC=120°,
∵ ∠D=60°,
∵ DE=BD-BE,
证明:
∴∠BCD+∠DCB=120°.
∴∠BCD+∠ADE=120°.
∵ ∠1=60°,
∴∠1=∠D.
AB=BC
在△ABE和△BCD中,
∠ABE=∠BCD
∠1=∠D
(AAS)
A
B
C
D
E
F
证明:
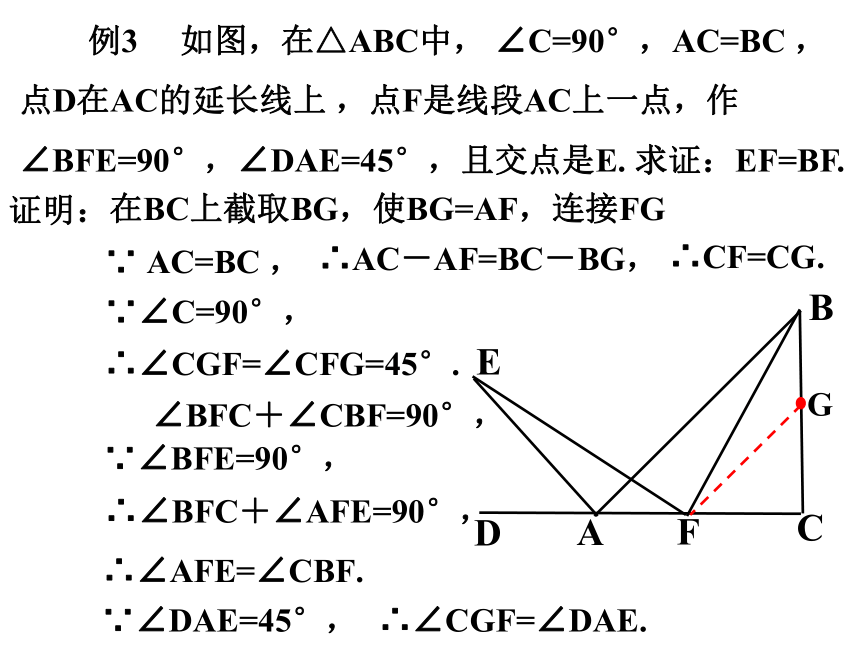
在BC上截取BG,使BG=AF,连接FG
G
∵∠BFE=90°,
∵∠C=90°,
∠BFC+∠CBF=90°,
例3 如图,在△ABC中, ∠C=90°,AC=BC ,点D在AC的延长线上 ,点F是线段AC上一点,作∠BFE=90°,∠DAE=45°,且交点是E. 求证:EF=BF.
∴∠BFC+∠AFE=90°,
∴∠AFE=∠CBF.
∵∠DAE=45°,
∵ AC=BC ,
∴AC-AF=BC-BG,
∴CF=CG.
∴∠CGF=∠CFG=45°.
∴∠CGF=∠DAE.
A
B
C
D
E
F
证明:
在BC上截取BG,使BG=AF,连接FG
G
∵∠BFE=90°,
∵∠C=90°,
∠BFC+∠CBF=90°.
∴∠BFC+∠AFE=90°,
∴∠AFE=∠CBF.
∵∠DAE=45°,
∵ AC=BC ,
∴AC-AF=BC-BG,
∴CF=CG.
∴∠CGF=∠CFG=45°,
∴∠CGF=∠DAE.
∵ ∠DAE+∠EAF=180°,
∠CGF+∠BGF=180°,
∴∠EAF=∠BGF.
∴EF=BF.
∴△AFE≌△CFB.
(ASA)
1.下列给出的三角形全等判定简记中,不能判定两个三角形全等的是( ).
练习巩固
A.SSA
B.SAS
C.ASA
D.AAS
2.如图,已知两个三角形全等,则x的度数
是( ).
A.30 B. 45 C. 50 D. 85
A
3
105°
x°
3
105°
45°
A
3. 如图,△ABC≌△ADE,∠A=41°,∠B=51°, 则∠1=( ).
A.88° B. 92° C. 132° D. 143°
A
C
D
1
B
E
D
4. 如图,已知AC与BD相交于点E,∠1=∠2.
若用“SAS”说明△ABC≌△DCB,则还需添加的一个条件是( ).
A.AD=BC B.AE=DE
C.BE=CE D. AC=DB
D
A
B
C
D
E
1
2
5. 如图,已知∠1=∠2. 若要用“ASA”说明△ACB≌△ADB,则还需添加的一个条件是( ).
A.CB=DB B.AC=AD
C.∠C=∠D D.∠ABC=∠ABD
D
1
2
B
A
C
D
6. 如图,已知AB⊥BD,CD ⊥ BD,若根据 “HL”判定Rt△ABD和Rt△CDB全等 ,则需补充的条件是( ).
A.AB=CD B. ∠A=∠C
C.BD=DB D.AD=CB
D
B
C
D
A
7.如图所示,AC=CD,∠B=∠E=90°,
AC⊥CD,则不一定成立的结论是( ).
A.∠A与∠D互为余角 B.∠A=∠2
C.△ABC≌△CED D.∠1=∠2
D
A
B
C
D
1
2
E
8.如图,已知∠1=∠2,要△ABD≌△ACD,
还需从下列条件中补选一个,则错误的选法
是( ).
A.AB=AC B.DB=DC
C. ∠ADB=∠ADC D.∠B=∠C
B
(SAS)
(ASA)
(AAS)
A
B
C
D
1
2
9.如图,AB=AD,∠1=∠D,下列条件
不一定能使△ABC和△ACD全等的条件是( ).
A.∠B=∠2 B.∠3=∠4
C. ∠3=∠2 D.AC=CD
C
A
B
C
D
2
4
3
1
10. 如图,已知AB=DC,∠ABC=∠DCB,则能直接证明△ABC≌△DCB的方法是 ( 填写字母).若∠ A=57°,则∠ D的度数是 .
57°
A
B
C
D
SAS
11.如图,已知∠B=∠E ,AB=DE . 若要根据“AAS”判定△ABC≌△DEF,则还需添加的条件是 .
∠BCA=∠EFD
A
B
C
D
E
F
12.已知,如图,△ABC≌△EBD,AC=ED,
则AB= , ∠ABC= .
A
B
C
E
D
EB
∠EBD
13.已知,如图,AE=AD,要使△ABD≌△ACE,
请你增加一个条件是 .
AB=AC
∠B=∠C
∠BDA =∠CEA
∠CDB=∠BEC
A
B
C
D
E
14.如图,点B、E、C、F在一条直线上,AB=DC,
AE=DF,BF=CE.
证明:
AB=DC
AE=DF
BE=CF
∴△ABE≌△DCF
D
A
B
C
E
F
在△ABE和△DCF中
∵BF=CE,
∴BF-EF=CE-EF,
∴BE=CF.
(SSS)
求证:AB∥DC.
(已知)
(等式的性质)
(已知)
(已知)
(已证)
∴AB∥DC.
∴∠B=∠C.
(全等三角形的对应角相等)
(内错角相等,两直线平行)
(等式的性质)
15.如图,已知,AC=EC,∠BCE=∠DCA,∠A=∠E. 求证:BC=DC.
∵∠BCE=∠DCA,
证明:
∴∠BCE+∠ECA
∠DCA+∠ECA,
∴∠BCA=∠DCE.
在ΔBCA和ΔDCE中,
AC=EC
∠BCA=∠DCE
∠A=∠E
∴ ΔBCA≌ΔDCE
∴BC=DC.
=
(ASA)
A
B
C
D
E
16. 如图,已知AC=BD, BC、AD相交于点E,且BC⊥AC,BD⊥AD. AD 是∠BAC的平分线. 求证:BC
是∠ABD的平分线.
A
B
C
D
∵ BC⊥AC,BD⊥AD,
证明:
∴∠C=∠D=90°.
在△RtABC和Rt△BAD中
AC=BD
AB=BA
∴ △RtABC ≌ Rt△BAD
∴∠CBA =∠DAB,
∠BAC =∠ABD,
∵ AD 是∠BAC的平分线,
∴∠BAC =2∠DAB,
∴∠ABD =2∠CBA,
∴ BC是∠ABD的平分线.
(HL)
17.如图,在直线AB上分别作AD⊥AB、BC⊥AB,垂足分别是A、B,AD>BC,连接CD交AB于点E.在AD上取点F,使FD=BC,连接BF交CD于点O.作FG ⊥ AD,交CD于点G. 求证:EO=GO.
A
B
C
D
E
F
G
O
证明:
∵AD⊥AB、BC⊥AB,
∴AD∥BC.
∴∠C=∠D.
∵FG ⊥ AD,
∴∠A=∠CBA=90°.
∴∠GFD=90°.
∴∠A=∠GFD=90°.
∴AB∥FG,
∴∠ABF=∠GFB.
∵FD=BC,
∴ ΔFDG≌ΔBCE.
(ASA)
∴ FG=BE.
∵∠EOB=∠GOF.
∴ ΔEOB≌ΔGOF.
∴EO=GO.
第14章 全等三角形的判定
全等三角形的对应边上的高相等.
全等三角形的对应边上的中线相等.
全等三角形的对应角的平分线相等.
全等三角形的对应边相等.
全等三角形的对应角相等.
2.全等三角形的性质:
复习要点
能够完全重合的两个三角形称为全等三角形.
1.全等三角形的定义
3.全等三角形的判定方法
一般三角形:
SSS
SAS
ASA
AAS
直角三角形:
HL
SAS
ASA
AAS
判定两个三角形全等的条件中
至少有一组边对应相等.
结论:
复习要点
复习要点
4.
判
定
全
等
的
思
路
首先
找边S
S
S
A
SAS
A
A
ASA
AAS
SSS
HL
判定两个三角形全等的条件中至少有
一组边对应相等.
例1 如图,△ABC中,AD⊥BC于D,BE⊥AC
于E,AD交BE于F,若BF=AC. 求证:AD=BD.
AD⊥BC,BE⊥AC
△BFD≌△ACD
AD=BD
∠1=∠2.
∠BDA=∠ADC=∠BEC= 90°
要证:
例题解析
1
2
A
B
C
D
F
E
∵AD⊥BC,BE⊥AC,
∴△BFD≌△ACD
∴ AD=BD.
∴ ∠1=∠2.
BF=AC
∠2 + ∠C= 90°,
∴ ∠1 + ∠C= 90°,
∴∠BDA=∠ADC=∠BEC= 90°
在△BFD和△ACD中,
∠BDF=∠ADC
∠1=∠2
证明:
(AAS)
1
2
A
B
C
D
F
E
例1 如图,△ABC中,AD⊥BC于D,BE⊥AC
于E,AD交BE于F,若BF=AC. 求证:AD=BD.
例2 如图,在△ABC中, ∠ABC=120°, AB=BC,BD是∠ABC内的射线 ,若连接DC, ∠D=60°,点E是线段BD上一点,且∠1=60°. 求证:DE=AE-DC.
A
B
C
D
E
1
要证:DE=AE-DC
AE=BD
DC=BE
要证:
要证:
△ABE≌△BCD
∠ABE=∠BCD.
∠ABC=120°
∠D=60°
例2 如图,在△ABC中, ∠ABC=120°, AB=BC,BD是∠ABC内的射线 ,若连接DC, ∠D=60°,点E是线段BD上一点,且∠1=60°. 求证:DE=AE-DC.
A
B
C
D
E
1
∴DE=AE-DC.
∴AE=BD,
DC=BE.
∴△ABE≌△BCD.
∴∠ABE=∠BCD.
∵ ∠ABC=120°,
∵ ∠D=60°,
∵ DE=BD-BE,
证明:
∴∠BCD+∠DCB=120°.
∴∠BCD+∠ADE=120°.
∵ ∠1=60°,
∴∠1=∠D.
AB=BC
在△ABE和△BCD中,
∠ABE=∠BCD
∠1=∠D
(AAS)
A
B
C
D
E
F
证明:
在BC上截取BG,使BG=AF,连接FG
G
∵∠BFE=90°,
∵∠C=90°,
∠BFC+∠CBF=90°,
例3 如图,在△ABC中, ∠C=90°,AC=BC ,点D在AC的延长线上 ,点F是线段AC上一点,作∠BFE=90°,∠DAE=45°,且交点是E. 求证:EF=BF.
∴∠BFC+∠AFE=90°,
∴∠AFE=∠CBF.
∵∠DAE=45°,
∵ AC=BC ,
∴AC-AF=BC-BG,
∴CF=CG.
∴∠CGF=∠CFG=45°.
∴∠CGF=∠DAE.
A
B
C
D
E
F
证明:
在BC上截取BG,使BG=AF,连接FG
G
∵∠BFE=90°,
∵∠C=90°,
∠BFC+∠CBF=90°.
∴∠BFC+∠AFE=90°,
∴∠AFE=∠CBF.
∵∠DAE=45°,
∵ AC=BC ,
∴AC-AF=BC-BG,
∴CF=CG.
∴∠CGF=∠CFG=45°,
∴∠CGF=∠DAE.
∵ ∠DAE+∠EAF=180°,
∠CGF+∠BGF=180°,
∴∠EAF=∠BGF.
∴EF=BF.
∴△AFE≌△CFB.
(ASA)
1.下列给出的三角形全等判定简记中,不能判定两个三角形全等的是( ).
练习巩固
A.SSA
B.SAS
C.ASA
D.AAS
2.如图,已知两个三角形全等,则x的度数
是( ).
A.30 B. 45 C. 50 D. 85
A
3
105°
x°
3
105°
45°
A
3. 如图,△ABC≌△ADE,∠A=41°,∠B=51°, 则∠1=( ).
A.88° B. 92° C. 132° D. 143°
A
C
D
1
B
E
D
4. 如图,已知AC与BD相交于点E,∠1=∠2.
若用“SAS”说明△ABC≌△DCB,则还需添加的一个条件是( ).
A.AD=BC B.AE=DE
C.BE=CE D. AC=DB
D
A
B
C
D
E
1
2
5. 如图,已知∠1=∠2. 若要用“ASA”说明△ACB≌△ADB,则还需添加的一个条件是( ).
A.CB=DB B.AC=AD
C.∠C=∠D D.∠ABC=∠ABD
D
1
2
B
A
C
D
6. 如图,已知AB⊥BD,CD ⊥ BD,若根据 “HL”判定Rt△ABD和Rt△CDB全等 ,则需补充的条件是( ).
A.AB=CD B. ∠A=∠C
C.BD=DB D.AD=CB
D
B
C
D
A
7.如图所示,AC=CD,∠B=∠E=90°,
AC⊥CD,则不一定成立的结论是( ).
A.∠A与∠D互为余角 B.∠A=∠2
C.△ABC≌△CED D.∠1=∠2
D
A
B
C
D
1
2
E
8.如图,已知∠1=∠2,要△ABD≌△ACD,
还需从下列条件中补选一个,则错误的选法
是( ).
A.AB=AC B.DB=DC
C. ∠ADB=∠ADC D.∠B=∠C
B
(SAS)
(ASA)
(AAS)
A
B
C
D
1
2
9.如图,AB=AD,∠1=∠D,下列条件
不一定能使△ABC和△ACD全等的条件是( ).
A.∠B=∠2 B.∠3=∠4
C. ∠3=∠2 D.AC=CD
C
A
B
C
D
2
4
3
1
10. 如图,已知AB=DC,∠ABC=∠DCB,则能直接证明△ABC≌△DCB的方法是 ( 填写字母).若∠ A=57°,则∠ D的度数是 .
57°
A
B
C
D
SAS
11.如图,已知∠B=∠E ,AB=DE . 若要根据“AAS”判定△ABC≌△DEF,则还需添加的条件是 .
∠BCA=∠EFD
A
B
C
D
E
F
12.已知,如图,△ABC≌△EBD,AC=ED,
则AB= , ∠ABC= .
A
B
C
E
D
EB
∠EBD
13.已知,如图,AE=AD,要使△ABD≌△ACE,
请你增加一个条件是 .
AB=AC
∠B=∠C
∠BDA =∠CEA
∠CDB=∠BEC
A
B
C
D
E
14.如图,点B、E、C、F在一条直线上,AB=DC,
AE=DF,BF=CE.
证明:
AB=DC
AE=DF
BE=CF
∴△ABE≌△DCF
D
A
B
C
E
F
在△ABE和△DCF中
∵BF=CE,
∴BF-EF=CE-EF,
∴BE=CF.
(SSS)
求证:AB∥DC.
(已知)
(等式的性质)
(已知)
(已知)
(已证)
∴AB∥DC.
∴∠B=∠C.
(全等三角形的对应角相等)
(内错角相等,两直线平行)
(等式的性质)
15.如图,已知,AC=EC,∠BCE=∠DCA,∠A=∠E. 求证:BC=DC.
∵∠BCE=∠DCA,
证明:
∴∠BCE+∠ECA
∠DCA+∠ECA,
∴∠BCA=∠DCE.
在ΔBCA和ΔDCE中,
AC=EC
∠BCA=∠DCE
∠A=∠E
∴ ΔBCA≌ΔDCE
∴BC=DC.
=
(ASA)
A
B
C
D
E
16. 如图,已知AC=BD, BC、AD相交于点E,且BC⊥AC,BD⊥AD. AD 是∠BAC的平分线. 求证:BC
是∠ABD的平分线.
A
B
C
D
∵ BC⊥AC,BD⊥AD,
证明:
∴∠C=∠D=90°.
在△RtABC和Rt△BAD中
AC=BD
AB=BA
∴ △RtABC ≌ Rt△BAD
∴∠CBA =∠DAB,
∠BAC =∠ABD,
∵ AD 是∠BAC的平分线,
∴∠BAC =2∠DAB,
∴∠ABD =2∠CBA,
∴ BC是∠ABD的平分线.
(HL)
17.如图,在直线AB上分别作AD⊥AB、BC⊥AB,垂足分别是A、B,AD>BC,连接CD交AB于点E.在AD上取点F,使FD=BC,连接BF交CD于点O.作FG ⊥ AD,交CD于点G. 求证:EO=GO.
A
B
C
D
E
F
G
O
证明:
∵AD⊥AB、BC⊥AB,
∴AD∥BC.
∴∠C=∠D.
∵FG ⊥ AD,
∴∠A=∠CBA=90°.
∴∠GFD=90°.
∴∠A=∠GFD=90°.
∴AB∥FG,
∴∠ABF=∠GFB.
∵FD=BC,
∴ ΔFDG≌ΔBCE.
(ASA)
∴ FG=BE.
∵∠EOB=∠GOF.
∴ ΔEOB≌ΔGOF.
∴EO=GO.
