第21章二次函数与反比例函数期末复习(6)实际问题与二次函数 课件(共26张PPT)
文档属性
| 名称 | 第21章二次函数与反比例函数期末复习(6)实际问题与二次函数 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 984.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 15:48:32 | ||
图片预览






文档简介
(共26张PPT)
第21章二次函数与反比例函数期末复习(6)
二次函数的与实际问题
沪科版
复习要点 二次函数与实际问题
用函数观点解决实际问题需要掌握什么
(1)要对实际问题中变量与变量之间的关系熟练掌握.
(2)将量与量之间的关系看作函数关系,用函数思想
进行分析.
(3)利用函数的图象与有关性质解决实际问题
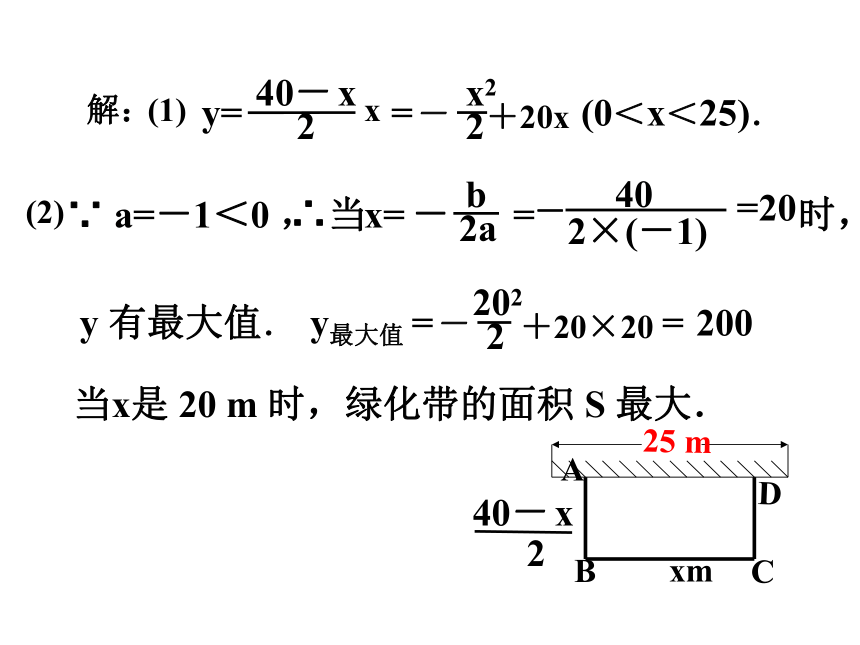
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y m2.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
例题解析1 几何问题的最值
D
C
B
A
25 m
xm
40
2
- x
解:
(1)
y=
40
2
- x
x
=-
2
x2
+20x
(0<x<25).
∴当 时,
y 有最大值.
∵ a=-1<0 ,
y最大值
x=
b
2a
-
40
2×(-1)
=20
=
=-
2
202
+20×20
=
200
(2)
当x是 20 m 时,绿化带的面积 S 最大.
-
1.解决几何图形中的最值问题的关键是根据图形
的特点和相关计算公式建立二次函数表达式,
再利用二次函数的性质,特别是顶点坐标来解
决问题,注意保证图形存在并有实际意义,所
以通常要对自变量限定取值范围.
规律方法总结
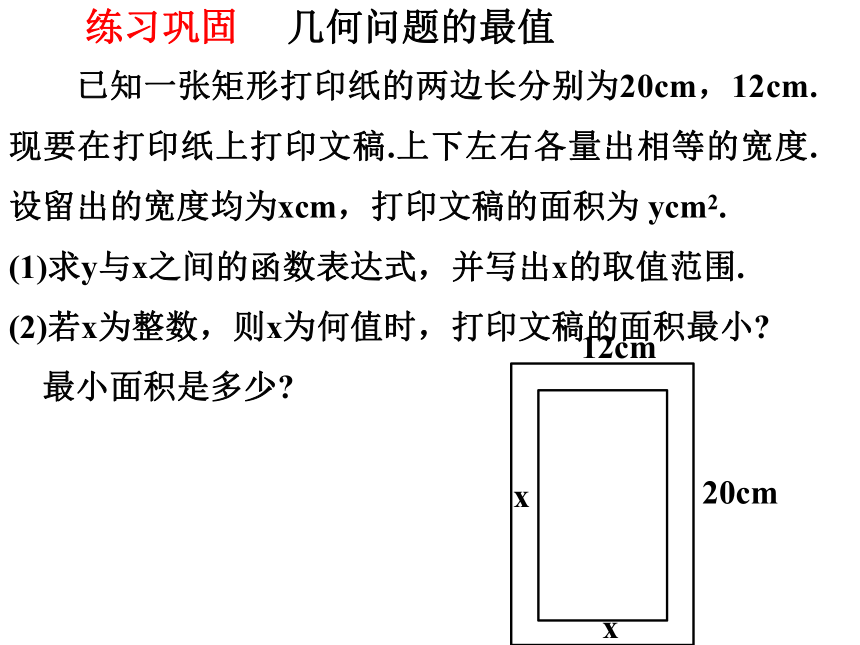
已知一张矩形打印纸的两边长分别为20cm,12cm.现要在打印纸上打印文稿.上下左右各量出相等的宽度.设留出的宽度均为xcm,打印文稿的面积为 ycm2.
(1)求y与x之间的函数表达式,并写出x的取值范围.
(2)若x为整数,则x为何值时,打印文稿的面积最小
最小面积是多少
x
x
20cm
12cm
练习巩固 几何问题的最值
已知一张矩形打印纸的两边长分别为20cm,12cm.现要在打印纸上打印文稿.上下左右各量出相等的宽度.设留出的宽度均为xcm,打印文稿的面积为 ycm2.
(1)求y与x之间的函数表达式,并写出x的取值范围.
解:
(1)
x
x
20cm
12cm
根据题意,打印文稿的
长为(20-2x)cm,宽为(12-2x)cm
∴ y=
(12-2x)
(20-2x)
=240-40x-24x+4x2
=4x2-64x+240
∵ 0<12-2x<12
∴ 0<x<6
x
x
20cm
12cm
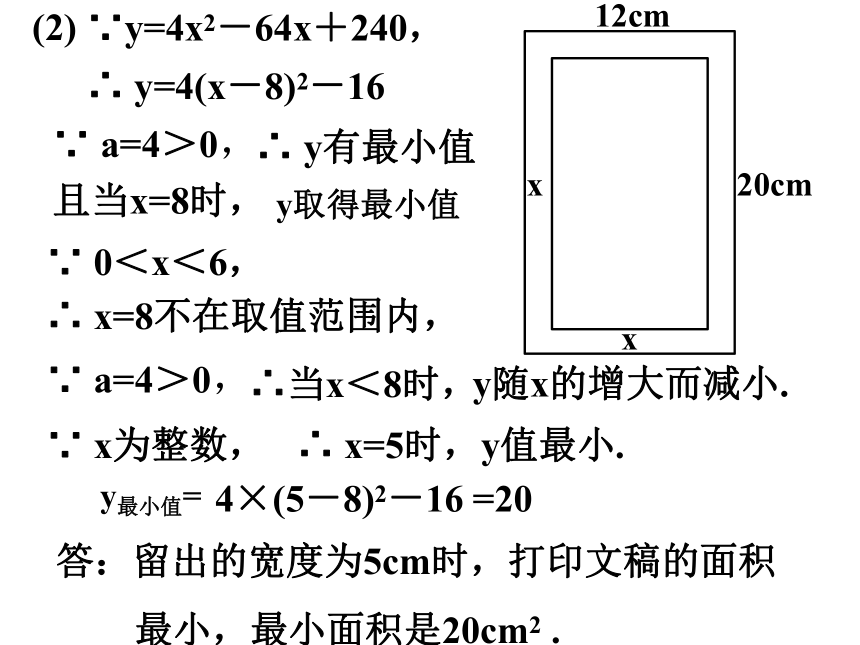
∵y=4x2-64x+240,
∵ 0<x<6,
(2)
∴ y=4(x-8)2-16
∵ a=4>0,
∴ y有最小值
∵ x为整数,
∴ x=5时,y值最小.
y最小值=
4×(5-8)2-16
=20
答:留出的宽度为5cm时,打印文稿的面积
最小,最小面积是20cm2 .
且当x=8时,
y取得最小值
∴ x=8不在取值范围内,
∵ a=4>0,
∴当x<8时,
y随x的增大而减小.
某旅馆有30个房间供旅客住宿.据测算,若每个房间的定价为60元/天,房间会住满;若每个房间的定价每增加5元,就会有一个房间空闲,该旅馆对旅客住宿的房间每间要支出各种费用20元/天(没住宿不支出).当房价定为每天多少时,该旅馆每天的利润最大?
例题解析2 求利润的最大值
某旅馆有30个房间供旅客住宿.据测算,若每个房间的定价为60元/天,房间会住满;若每个房间的定价每增加5元,就会有一个房间空闲,该旅馆对旅客住宿的房间每间要支出各种费用20元/天(没住宿不支出).当房价定为每天多少时,该旅馆每天的利润最大?
解:设房价定为每天x元,利润为y元.
y=
整理,得
y=- x2+46x-840
∴y有最大值,
∵ a=- <0 ,
(30- )
(x-20)
x-60
5
5
1
5
1
解:设房价定为每天x元,每天的利润为y元.
y=
整理,得
y=- x2+46x-840
∴y有最大值,
∴当房价定为每天115元时,旅馆每天的利润最大.
∵ a=- <0 ,
(30- )
(x-20)
x-60
5
5
1
5
1
y最大值=
c
b2
4a
-
=-840
462
4×(- )
=1805.
相应的x值为
b
2a
x=-
46
2×(- )
=115
-
5
1
=
5
1
2.利用二次函数解决实际问题中的最值问题,
首先要根据题意建立二次函数表达式,然后
再利用配方法(或公式法)求出何时获得最值,
从而使问题得到解决.
规律方法总结
解:设定价为x元,利润为y元,
y=
则有
整理,得
y=-20x2+2300x-60000
∴y有最大值,
∴当定价 57.5 元 时,销售利润y最大.
∵ a=-20<0 ,
某商品现在的售价为每件 60 元,每星期可卖出300件.市场调查反映:如调整价格,每涨价 1 元,每星期要少卖出 10 件;每降价 1 元,每星期可多卖出 20 件.已知商品的进价为每件 40 元,如何定价才能使利润最大?
[300+20(60-x)]
(x-40)
相应的x值为
x=
-
=
b
2a
-
2300
2×(-20)
=57.5
练习巩固
5 m
A
B
4 m
16 m
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
(1)求水面宽度增加多少需要什么数据?
需要知道水面下降 5 m后的水面宽度.
如AB.
生活中的抛物线形问题
例题解析3
5 m
(1)求水面宽度增加多少需要什么数据?
需要知道水面下降 5 m后的水面宽度.
A
B
(2)表示水面宽度的线段的端点在哪条曲线上?
抛物线
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
4 m
16 m
5 m
A
B
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
4 m
16 m
(2)表示水面宽的线
段的端点在哪条
曲线上?
(3)如何求出A、B两点的坐标?
要知道A、B两点所在的抛物线解析式.
抛物线
5 m
A
B
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
4 m
16 m
(3)如何求出A、B
两点的坐标?
(4)怎样确定A、B两点所在的抛物线解析式?
要知道A、B两点所在的抛物线解析式
建立适当的坐标系.
5 m
A
B
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
4 m
16 m
(5)如何建立直角坐标系?
(4)怎样确定A、B两点所在
的抛物线解析式?
建立适当的坐标系.
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
x
y
O
x
y
O
4
8
-4
-8
-4
-8
A
B
(8,-4)
C
D
E
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
设抛物线的解析式为y=ax2.
拱顶OE离水面 4 m
水面CD宽 16 m
设抛物线的解析式为y=ax2.
∵抛物线经过点D(8,-4),
∴-4=a×82.
∴a=- .
∴抛物线的解析式为
当水面下降 5 m时,
即y=-9.
∴-9=- x2,
∴x1=-12,
24.
∴AB=
水面下降 5 m时,
水面宽度增加8m.
1
16
1
16
1
16
x2=12.
x
y
O
4
8
-4
-8
-4
-8
A
B
(8,-4)
C
D
E
y=- x2.
拱顶OF离水面 9 m
F
∴AB-CD=24-16=8
3.解决生活中拱桥、喷泉、篮球轨迹等问题,关
键是把实际问题转化为二次函数的模型,恰当
地选择平面直角坐标系,并和用二次函数的性
质解决实际问题.
规律方法总结
3.燃放烟花是一种常见的喜庆活动,小杰燃放一种手持烟花,这种烟花每隔2s发射一枚花弹,每枚花弹的飞行路径视为同一条抛物线,飞行相同时间后发生爆炸,小杰发射出的第一枚弹的飞行高度h(单位:m)随飞行时间t(单位:s)变化的规律如下表:
飞行时间 t/s 0 0.5 1 4.5 ...
飞行高度h/m 2 9.5 16 33.5 …
(1)求第一花弹的飞行高度h与飞行时间t的函数解析式
(不要求写出自变量的取值范围);
练习巩固
(2)当第一花弹到达最高点时,求第二枚花弹到达的高度;
(3)为了安全,要求花弹爆炸时的高度不低于30m,小杰发现在第一枚花弹爆炸的同时,第二枚花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求.
∵每枚花弹的飞行路径视为同一条抛物线,
∴第一枚花弹的飞行高度h与飞行时间t的函数解析式
为 h=at2+bt+2,
第一枚花弹的飞行高度h与飞行时间t的函数解析式为
h= -2t2+16t+2.
0.25a +0.5b+c=9.5.
a+b+c=16
a=-2
∴
b=16
∴
解: (1)
(2) ∵ h= -2t2+16t+2
∴当t=4时,第一枚花弹到达最高点.
∵这种烟花每隔2s发射一枚花弹,每枚花弹的飞行路径视为同一条抛物线,
∴第二枚花弹的飞行高度h与飞行时间t的函数解析式是
h= -2t2+16t+2.
∴当第一枚花弹到达最高点时,第二枚花弹飞行时间
t=2
= -2(t-4) +34
当t=2时,h=
-2 × 2 +16 × 2+2=26(米).
∴当第一枚花弹到达最高点时,第二枚花弹到达的高度为26米.
(3)花弹的爆炸高度符合安全要求,理由如下:
由(1)(2)可知:第一枚花弹的飞行高度h与飞行时间t的函数解析式为 h= -2t2+16t+2,
第二枚花弹的飞行高度h与飞行时间t的函数解析式是
h=-2(t+2)2+16(t+2)+2,
第一枚花弹爆炸的同时,第二枚花弹与它处于同一高度
∴ -2(t+2)2+16(t+2)+2= -2t2+16t+2. ,
∴ t=3.
当t=3时,h= -2×32+16×3+2=32(米)
∵ 32>30,
∴花弹的爆炸高度符合安全要求.
第21章二次函数与反比例函数期末复习(6)
二次函数的与实际问题
沪科版
复习要点 二次函数与实际问题
用函数观点解决实际问题需要掌握什么
(1)要对实际问题中变量与变量之间的关系熟练掌握.
(2)将量与量之间的关系看作函数关系,用函数思想
进行分析.
(3)利用函数的图象与有关性质解决实际问题
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y m2.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
例题解析1 几何问题的最值
D
C
B
A
25 m
xm
40
2
- x
解:
(1)
y=
40
2
- x
x
=-
2
x2
+20x
(0<x<25).
∴当 时,
y 有最大值.
∵ a=-1<0 ,
y最大值
x=
b
2a
-
40
2×(-1)
=20
=
=-
2
202
+20×20
=
200
(2)
当x是 20 m 时,绿化带的面积 S 最大.
-
1.解决几何图形中的最值问题的关键是根据图形
的特点和相关计算公式建立二次函数表达式,
再利用二次函数的性质,特别是顶点坐标来解
决问题,注意保证图形存在并有实际意义,所
以通常要对自变量限定取值范围.
规律方法总结
已知一张矩形打印纸的两边长分别为20cm,12cm.现要在打印纸上打印文稿.上下左右各量出相等的宽度.设留出的宽度均为xcm,打印文稿的面积为 ycm2.
(1)求y与x之间的函数表达式,并写出x的取值范围.
(2)若x为整数,则x为何值时,打印文稿的面积最小
最小面积是多少
x
x
20cm
12cm
练习巩固 几何问题的最值
已知一张矩形打印纸的两边长分别为20cm,12cm.现要在打印纸上打印文稿.上下左右各量出相等的宽度.设留出的宽度均为xcm,打印文稿的面积为 ycm2.
(1)求y与x之间的函数表达式,并写出x的取值范围.
解:
(1)
x
x
20cm
12cm
根据题意,打印文稿的
长为(20-2x)cm,宽为(12-2x)cm
∴ y=
(12-2x)
(20-2x)
=240-40x-24x+4x2
=4x2-64x+240
∵ 0<12-2x<12
∴ 0<x<6
x
x
20cm
12cm
∵y=4x2-64x+240,
∵ 0<x<6,
(2)
∴ y=4(x-8)2-16
∵ a=4>0,
∴ y有最小值
∵ x为整数,
∴ x=5时,y值最小.
y最小值=
4×(5-8)2-16
=20
答:留出的宽度为5cm时,打印文稿的面积
最小,最小面积是20cm2 .
且当x=8时,
y取得最小值
∴ x=8不在取值范围内,
∵ a=4>0,
∴当x<8时,
y随x的增大而减小.
某旅馆有30个房间供旅客住宿.据测算,若每个房间的定价为60元/天,房间会住满;若每个房间的定价每增加5元,就会有一个房间空闲,该旅馆对旅客住宿的房间每间要支出各种费用20元/天(没住宿不支出).当房价定为每天多少时,该旅馆每天的利润最大?
例题解析2 求利润的最大值
某旅馆有30个房间供旅客住宿.据测算,若每个房间的定价为60元/天,房间会住满;若每个房间的定价每增加5元,就会有一个房间空闲,该旅馆对旅客住宿的房间每间要支出各种费用20元/天(没住宿不支出).当房价定为每天多少时,该旅馆每天的利润最大?
解:设房价定为每天x元,利润为y元.
y=
整理,得
y=- x2+46x-840
∴y有最大值,
∵ a=- <0 ,
(30- )
(x-20)
x-60
5
5
1
5
1
解:设房价定为每天x元,每天的利润为y元.
y=
整理,得
y=- x2+46x-840
∴y有最大值,
∴当房价定为每天115元时,旅馆每天的利润最大.
∵ a=- <0 ,
(30- )
(x-20)
x-60
5
5
1
5
1
y最大值=
c
b2
4a
-
=-840
462
4×(- )
=1805.
相应的x值为
b
2a
x=-
46
2×(- )
=115
-
5
1
=
5
1
2.利用二次函数解决实际问题中的最值问题,
首先要根据题意建立二次函数表达式,然后
再利用配方法(或公式法)求出何时获得最值,
从而使问题得到解决.
规律方法总结
解:设定价为x元,利润为y元,
y=
则有
整理,得
y=-20x2+2300x-60000
∴y有最大值,
∴当定价 57.5 元 时,销售利润y最大.
∵ a=-20<0 ,
某商品现在的售价为每件 60 元,每星期可卖出300件.市场调查反映:如调整价格,每涨价 1 元,每星期要少卖出 10 件;每降价 1 元,每星期可多卖出 20 件.已知商品的进价为每件 40 元,如何定价才能使利润最大?
[300+20(60-x)]
(x-40)
相应的x值为
x=
-
=
b
2a
-
2300
2×(-20)
=57.5
练习巩固
5 m
A
B
4 m
16 m
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
(1)求水面宽度增加多少需要什么数据?
需要知道水面下降 5 m后的水面宽度.
如AB.
生活中的抛物线形问题
例题解析3
5 m
(1)求水面宽度增加多少需要什么数据?
需要知道水面下降 5 m后的水面宽度.
A
B
(2)表示水面宽度的线段的端点在哪条曲线上?
抛物线
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
4 m
16 m
5 m
A
B
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
4 m
16 m
(2)表示水面宽的线
段的端点在哪条
曲线上?
(3)如何求出A、B两点的坐标?
要知道A、B两点所在的抛物线解析式.
抛物线
5 m
A
B
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
4 m
16 m
(3)如何求出A、B
两点的坐标?
(4)怎样确定A、B两点所在的抛物线解析式?
要知道A、B两点所在的抛物线解析式
建立适当的坐标系.
5 m
A
B
图中是抛物线形拱桥,当拱顶离水面 4m时,水面宽16m . 水面下降5m,水面宽度增加多少?
4 m
16 m
(5)如何建立直角坐标系?
(4)怎样确定A、B两点所在
的抛物线解析式?
建立适当的坐标系.
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
x
y
O
x
y
O
4
8
-4
-8
-4
-8
A
B
(8,-4)
C
D
E
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
设抛物线的解析式为y=ax2.
拱顶OE离水面 4 m
水面CD宽 16 m
设抛物线的解析式为y=ax2.
∵抛物线经过点D(8,-4),
∴-4=a×82.
∴a=- .
∴抛物线的解析式为
当水面下降 5 m时,
即y=-9.
∴-9=- x2,
∴x1=-12,
24.
∴AB=
水面下降 5 m时,
水面宽度增加8m.
1
16
1
16
1
16
x2=12.
x
y
O
4
8
-4
-8
-4
-8
A
B
(8,-4)
C
D
E
y=- x2.
拱顶OF离水面 9 m
F
∴AB-CD=24-16=8
3.解决生活中拱桥、喷泉、篮球轨迹等问题,关
键是把实际问题转化为二次函数的模型,恰当
地选择平面直角坐标系,并和用二次函数的性
质解决实际问题.
规律方法总结
3.燃放烟花是一种常见的喜庆活动,小杰燃放一种手持烟花,这种烟花每隔2s发射一枚花弹,每枚花弹的飞行路径视为同一条抛物线,飞行相同时间后发生爆炸,小杰发射出的第一枚弹的飞行高度h(单位:m)随飞行时间t(单位:s)变化的规律如下表:
飞行时间 t/s 0 0.5 1 4.5 ...
飞行高度h/m 2 9.5 16 33.5 …
(1)求第一花弹的飞行高度h与飞行时间t的函数解析式
(不要求写出自变量的取值范围);
练习巩固
(2)当第一花弹到达最高点时,求第二枚花弹到达的高度;
(3)为了安全,要求花弹爆炸时的高度不低于30m,小杰发现在第一枚花弹爆炸的同时,第二枚花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求.
∵每枚花弹的飞行路径视为同一条抛物线,
∴第一枚花弹的飞行高度h与飞行时间t的函数解析式
为 h=at2+bt+2,
第一枚花弹的飞行高度h与飞行时间t的函数解析式为
h= -2t2+16t+2.
0.25a +0.5b+c=9.5.
a+b+c=16
a=-2
∴
b=16
∴
解: (1)
(2) ∵ h= -2t2+16t+2
∴当t=4时,第一枚花弹到达最高点.
∵这种烟花每隔2s发射一枚花弹,每枚花弹的飞行路径视为同一条抛物线,
∴第二枚花弹的飞行高度h与飞行时间t的函数解析式是
h= -2t2+16t+2.
∴当第一枚花弹到达最高点时,第二枚花弹飞行时间
t=2
= -2(t-4) +34
当t=2时,h=
-2 × 2 +16 × 2+2=26(米).
∴当第一枚花弹到达最高点时,第二枚花弹到达的高度为26米.
(3)花弹的爆炸高度符合安全要求,理由如下:
由(1)(2)可知:第一枚花弹的飞行高度h与飞行时间t的函数解析式为 h= -2t2+16t+2,
第二枚花弹的飞行高度h与飞行时间t的函数解析式是
h=-2(t+2)2+16(t+2)+2,
第一枚花弹爆炸的同时,第二枚花弹与它处于同一高度
∴ -2(t+2)2+16(t+2)+2= -2t2+16t+2. ,
∴ t=3.
当t=3时,h= -2×32+16×3+2=32(米)
∵ 32>30,
∴花弹的爆炸高度符合安全要求.
