第22章相似形期末复习(2)相似三角形 课件(共27张PPT)
文档属性
| 名称 | 第22章相似形期末复习(2)相似三角形 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 822.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 15:54:46 | ||
图片预览








文档简介
(共27张PPT)
第22章 相似形期末复习(2)
沪科版
相似三角形
复习要点
2.三角形相似的判定方法
(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似;
(2)三组对应边的比相等的两个三角形相似;
(3)两组对应边成比例且夹角相等的两个三角形相似;
(4)两个角对应相等的两个三角形相似.
⑤有斜边和一直角边对应成比例的两个直角三角形相似;
⑥直角三角形被斜边上的高分成的两个直角三角形和
原三角形相似.
3.三角形相似的基本图形
如图①中,若DE∥BC,则△ADE∽△ABC;
图②中,若∠ADE=∠C,则△ADE∽△ACB;
图③中,若∠ACD=∠B,则△ACD∽△ABC;
图④中,若DE∥BC,则△ADE∽△ABC;
图⑤中,若∠ACB=∠CDB=90°,则
△ACD∽△CBD∽△ABC.
(2)相似三角形对应的 高、中线、角平分线 的比
等于相似比.
4.相似三角形的性质:
(4)相似三角形面积的比等于相似比的平方.
(3)相似三角形周长的比等于相似比.
(1)相似三角形对应角 ,对应边 .
相等
成比例
例1.根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
AB=8 , BC=12 , AC=18
A′B′=12 , B′C′=18 , A′C′=27
答:△ABC与△A′B′C′相似.
∵ AB:A′B′=8:12=2:3
BC:B′C′=12:18=2:3
AC:A′C′=18:27=2:3
∴ AB:A′B′=BC:B′C′=AC:A′C′.
例题解析
例2.如图所示,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.判断△ABC和△DEF是否相似,并说明理由.
△ABC和△DEF相似,
理由如下:
∵ AB=
5 ,
2
BC=5,
AC= ,
5
DE=
2 ,
4
DF=
2 ,
2
EF=
10 ,
2
∴ AB:DE=BC:=AC:DF= :4 .
10
解:
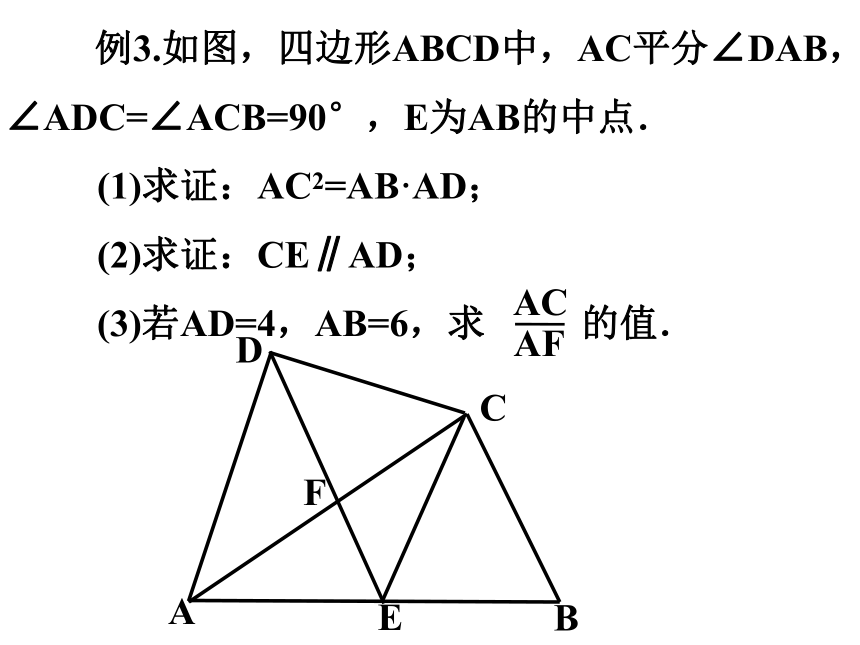
例3.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB·AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 的值.
A
B
C
D
E
F
AC
AF
例3.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB·AD;
A
B
C
D
E
F
∵ AC平分∠DAB,
(1)证明:
∴ ∠DAC=∠CAB ,
∵ ∠ADC=∠ACB=90°,
∴ △ADC∽△ACB.
∴ AD:AC=AC:AB.
∴ AC2=AB·AD.
例3.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(2)求证:CE∥AD;
A
B
C
D
E
F
(2)证明:
E为AB的中点,
∵ ∠ACB=90°,
∴ AE=CE.
∴ ∠ACE=∠CAB ,
∵ ∠DAC=∠CAB ,
∴ ∠ACE=∠DAC ,
∴ CE∥AD.
例3.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(3)若AD=4,AB=6,求 的值.
A
B
C
D
E
F
AC
AF
(3)
∵ CE∥AD,
∴ CF:AF=CE:AD.
∵ AD=4,AB=6,
∴ CE=3,
∴ (AC-AF):AF=CE:AD.
∴ (AC-AF):AF=3:4.
∴4AC=7AF.
∴
AC
AF
=
7
4
1.如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论中不正确的是( ).
A.BC=2DE B.△ADE∽△ABC
C. D.S△ABC=3S△ADE
A
B
C
D
E
=
AD
AE
AB
AC
选择题
D
练习巩固
2.如图,△ABC中,AE交BC于点D,∠C=∠E. AD=4,BC=8,BD∶DC=5∶3,则DE的长等于( ).
A
B
C
D
E
A. B. C. D.
20
3
15
4
16
3
17
4
B
3.如图,在□ABCD中,E是AD边上的中点,连结BE,并延长BE交CD的延长线于点F,则△EDF与△BCF的周长之比是( ).
A.1∶2 B.1∶3 C.1∶4 D.1∶5
A
B
C
D
E
F
C
4.已知△ABC∽△DEF,若△ABC与△DEF的相似比为3∶4,则△ABC与△DEF的面积之比为( ).
A.4∶3 B.3∶4
C.16∶9 D.9∶16
D
5.如图,在△ABC中,点D,E分别在边AB,AC上,且 ,则S△ADE∶S四边形BCED的值为( ).
A.1∶ B.1∶2 C.1∶3 D.1∶4
A
B
C
D
E
=
AE
AB
AD
AC
=
1
2
3
C
6.如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( ).
A
B
C
D
E
A. B. C. D.
4
3
3
3
2
3
6
3
B
7.如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20 m,EC=10 m,CD=20 m,则河的宽度AB等于( ).
A.60 m B.40 m
C.30 m D.20 m
B
8.如图,身高为1.6m的某同学想测量一棵大树的高度,她沿树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,AC=0.8m,则树高为( ).
A.4.8m B.6.4m C.8m D.10m
D
A
C
B
E
B
1.如果一个三角形三边长分别为5、12、13,与其相似的三角形最大边是39,则该三角形最短的边长为 .
2.如图,△ABC∽△A′B′C′,它们的周长分别为60cm和72cm,且AB=15cm,B′C′=24cm,
求BC= cm,A′C′= cm.
A
B
C
A′
B′
C′
填空题
15
20
30
3.D是△ABC的边AB上的点, 请添加一个条件,使△ACD与△ABC相似, 这个条件是 .
A
D
C
B
4.在△ABC中,DE∥BC, 若DE=2 BC=8 ,
△ADE的周长为20,则 △ABC 的周长为 .
第3题
第4题
∠ACD=∠B
80
5.如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F,BE:AB=2:3,则△BEF与△CDF的周长比为 ;若△BEF的面积为8平方厘米,则△CDF的面积为 .
A
B
E
C
D
F
6.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m.
O
B
D
C
A
┏
┛
1m
16m
0.5m
?
第6题
2:3
18平方厘米
8
1.如图, ∠ABD=∠C , AD=2 , AC=8,
求AB.
A
B
C
D
∵ ∠ABD=∠C ,
解:
∠A=∠A
∴ △ADB∽△ABC.
∴ AB:AC=AD:AB.
∵ AD=2 , AC=8,
∴ AB:8=2:AB.
∴ AB2=16.
∴ AB=4.
解答题
2.如图,已知 ,
试说明∠BAD=∠CAE.
A
D
C
E
B
=
=
AB
AD
BC
DE
AC
AE
解:
=
=
AB
AD
BC
DE
AC
AE
∵
∴ △ADE∽△ABC
∴ ∠ABC=∠DAE ,
∴ ∠ABC-∠DAC=∠DAE-∠DAC,
∴ ∠BAD=∠CAE.
=
=
4
2
5
x
6
y
解:
=
=
4
x
5
2
6
y
=
=
4
x
5
y
6
2
当 时,
当 时,
当 时,
x=2.5,
y=3.
x=1.6,
y=2.4.
x= ,
y= .
4
3
5
3
画法不唯一,有三种画法.
3.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4 cm,5cm和 6cm,另一个三角形框架的一边长为2 cm,它的另外两条边长应当是多少?你有几种制作方案?
4.如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
解:
∵ AB=6,AE=9,
∴ BE2=AB2 +AE2=62+92
∠A=90°,
=117
∴ BE=3 .
∵△ABE∽△DEF,
∴ EF:BE=DE:AB.
∴ EF:3 =2:6.
∴ EF = .
13
13
13
5.如图, △ABC中,AB=8,AC=6,BC=9,
如果动点D以每秒2个单位长的速度,从点B出发
沿边BA向点A运动,直线DE//BC,交AC于E.
记x秒时DE的长度是y,写出y关于x的函数关系式.
B
C
A
D
E
∵ DE//BC,
解:
∴ DE:BC=AD:AB.
∴ y:9=(8-2x):8.
∴ 8y=9(8-2x).
∴ y=- x+9 .
1
4
第22章 相似形期末复习(2)
沪科版
相似三角形
复习要点
2.三角形相似的判定方法
(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似;
(2)三组对应边的比相等的两个三角形相似;
(3)两组对应边成比例且夹角相等的两个三角形相似;
(4)两个角对应相等的两个三角形相似.
⑤有斜边和一直角边对应成比例的两个直角三角形相似;
⑥直角三角形被斜边上的高分成的两个直角三角形和
原三角形相似.
3.三角形相似的基本图形
如图①中,若DE∥BC,则△ADE∽△ABC;
图②中,若∠ADE=∠C,则△ADE∽△ACB;
图③中,若∠ACD=∠B,则△ACD∽△ABC;
图④中,若DE∥BC,则△ADE∽△ABC;
图⑤中,若∠ACB=∠CDB=90°,则
△ACD∽△CBD∽△ABC.
(2)相似三角形对应的 高、中线、角平分线 的比
等于相似比.
4.相似三角形的性质:
(4)相似三角形面积的比等于相似比的平方.
(3)相似三角形周长的比等于相似比.
(1)相似三角形对应角 ,对应边 .
相等
成比例
例1.根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
AB=8 , BC=12 , AC=18
A′B′=12 , B′C′=18 , A′C′=27
答:△ABC与△A′B′C′相似.
∵ AB:A′B′=8:12=2:3
BC:B′C′=12:18=2:3
AC:A′C′=18:27=2:3
∴ AB:A′B′=BC:B′C′=AC:A′C′.
例题解析
例2.如图所示,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.判断△ABC和△DEF是否相似,并说明理由.
△ABC和△DEF相似,
理由如下:
∵ AB=
5 ,
2
BC=5,
AC= ,
5
DE=
2 ,
4
DF=
2 ,
2
EF=
10 ,
2
∴ AB:DE=BC:=AC:DF= :4 .
10
解:
例3.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB·AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 的值.
A
B
C
D
E
F
AC
AF
例3.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB·AD;
A
B
C
D
E
F
∵ AC平分∠DAB,
(1)证明:
∴ ∠DAC=∠CAB ,
∵ ∠ADC=∠ACB=90°,
∴ △ADC∽△ACB.
∴ AD:AC=AC:AB.
∴ AC2=AB·AD.
例3.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(2)求证:CE∥AD;
A
B
C
D
E
F
(2)证明:
E为AB的中点,
∵ ∠ACB=90°,
∴ AE=CE.
∴ ∠ACE=∠CAB ,
∵ ∠DAC=∠CAB ,
∴ ∠ACE=∠DAC ,
∴ CE∥AD.
例3.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(3)若AD=4,AB=6,求 的值.
A
B
C
D
E
F
AC
AF
(3)
∵ CE∥AD,
∴ CF:AF=CE:AD.
∵ AD=4,AB=6,
∴ CE=3,
∴ (AC-AF):AF=CE:AD.
∴ (AC-AF):AF=3:4.
∴4AC=7AF.
∴
AC
AF
=
7
4
1.如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论中不正确的是( ).
A.BC=2DE B.△ADE∽△ABC
C. D.S△ABC=3S△ADE
A
B
C
D
E
=
AD
AE
AB
AC
选择题
D
练习巩固
2.如图,△ABC中,AE交BC于点D,∠C=∠E. AD=4,BC=8,BD∶DC=5∶3,则DE的长等于( ).
A
B
C
D
E
A. B. C. D.
20
3
15
4
16
3
17
4
B
3.如图,在□ABCD中,E是AD边上的中点,连结BE,并延长BE交CD的延长线于点F,则△EDF与△BCF的周长之比是( ).
A.1∶2 B.1∶3 C.1∶4 D.1∶5
A
B
C
D
E
F
C
4.已知△ABC∽△DEF,若△ABC与△DEF的相似比为3∶4,则△ABC与△DEF的面积之比为( ).
A.4∶3 B.3∶4
C.16∶9 D.9∶16
D
5.如图,在△ABC中,点D,E分别在边AB,AC上,且 ,则S△ADE∶S四边形BCED的值为( ).
A.1∶ B.1∶2 C.1∶3 D.1∶4
A
B
C
D
E
=
AE
AB
AD
AC
=
1
2
3
C
6.如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( ).
A
B
C
D
E
A. B. C. D.
4
3
3
3
2
3
6
3
B
7.如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20 m,EC=10 m,CD=20 m,则河的宽度AB等于( ).
A.60 m B.40 m
C.30 m D.20 m
B
8.如图,身高为1.6m的某同学想测量一棵大树的高度,她沿树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,AC=0.8m,则树高为( ).
A.4.8m B.6.4m C.8m D.10m
D
A
C
B
E
B
1.如果一个三角形三边长分别为5、12、13,与其相似的三角形最大边是39,则该三角形最短的边长为 .
2.如图,△ABC∽△A′B′C′,它们的周长分别为60cm和72cm,且AB=15cm,B′C′=24cm,
求BC= cm,A′C′= cm.
A
B
C
A′
B′
C′
填空题
15
20
30
3.D是△ABC的边AB上的点, 请添加一个条件,使△ACD与△ABC相似, 这个条件是 .
A
D
C
B
4.在△ABC中,DE∥BC, 若DE=2 BC=8 ,
△ADE的周长为20,则 △ABC 的周长为 .
第3题
第4题
∠ACD=∠B
80
5.如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F,BE:AB=2:3,则△BEF与△CDF的周长比为 ;若△BEF的面积为8平方厘米,则△CDF的面积为 .
A
B
E
C
D
F
6.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m.
O
B
D
C
A
┏
┛
1m
16m
0.5m
?
第6题
2:3
18平方厘米
8
1.如图, ∠ABD=∠C , AD=2 , AC=8,
求AB.
A
B
C
D
∵ ∠ABD=∠C ,
解:
∠A=∠A
∴ △ADB∽△ABC.
∴ AB:AC=AD:AB.
∵ AD=2 , AC=8,
∴ AB:8=2:AB.
∴ AB2=16.
∴ AB=4.
解答题
2.如图,已知 ,
试说明∠BAD=∠CAE.
A
D
C
E
B
=
=
AB
AD
BC
DE
AC
AE
解:
=
=
AB
AD
BC
DE
AC
AE
∵
∴ △ADE∽△ABC
∴ ∠ABC=∠DAE ,
∴ ∠ABC-∠DAC=∠DAE-∠DAC,
∴ ∠BAD=∠CAE.
=
=
4
2
5
x
6
y
解:
=
=
4
x
5
2
6
y
=
=
4
x
5
y
6
2
当 时,
当 时,
当 时,
x=2.5,
y=3.
x=1.6,
y=2.4.
x= ,
y= .
4
3
5
3
画法不唯一,有三种画法.
3.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4 cm,5cm和 6cm,另一个三角形框架的一边长为2 cm,它的另外两条边长应当是多少?你有几种制作方案?
4.如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
解:
∵ AB=6,AE=9,
∴ BE2=AB2 +AE2=62+92
∠A=90°,
=117
∴ BE=3 .
∵△ABE∽△DEF,
∴ EF:BE=DE:AB.
∴ EF:3 =2:6.
∴ EF = .
13
13
13
5.如图, △ABC中,AB=8,AC=6,BC=9,
如果动点D以每秒2个单位长的速度,从点B出发
沿边BA向点A运动,直线DE//BC,交AC于E.
记x秒时DE的长度是y,写出y关于x的函数关系式.
B
C
A
D
E
∵ DE//BC,
解:
∴ DE:BC=AD:AB.
∴ y:9=(8-2x):8.
∴ 8y=9(8-2x).
∴ y=- x+9 .
1
4
