第23章 解直角三角形 期末复习(1) 课件(共25张PPT)
文档属性
| 名称 | 第23章 解直角三角形 期末复习(1) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 00:00:00 | ||
图片预览


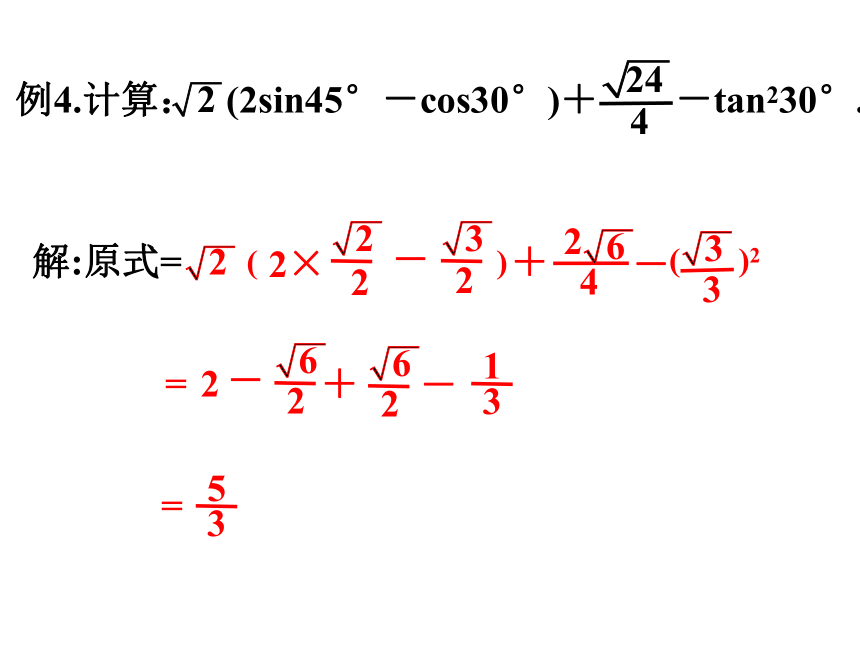
文档简介
(共25张PPT)
第23章 解直角三角形 期末复习(1)
锐角三角函数
沪科版
B
a
C
b
A
c
┏
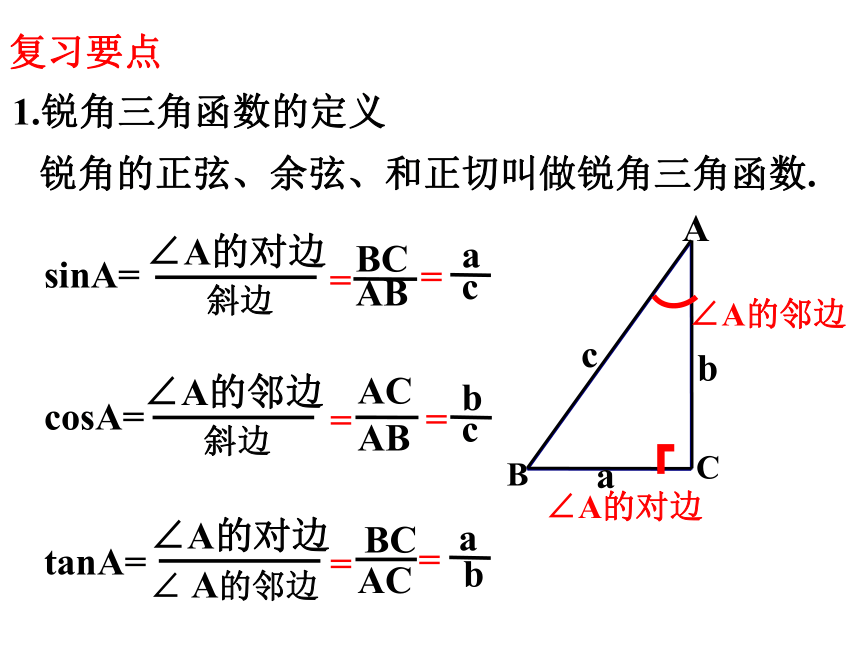
∠A的对边
斜边
∠A的对边
=
a
c
=
=
sinA=
BC
AB
=
cosA=
斜边
∠A的邻边
AC
AB
=
b
c
tanA=
∠ A的邻边
∠A的对边
BC
AC
=
a
b
∠A的邻边
1.锐角三角函数的定义
锐角的正弦、余弦、和正切叫做锐角三角函数.
复习要点
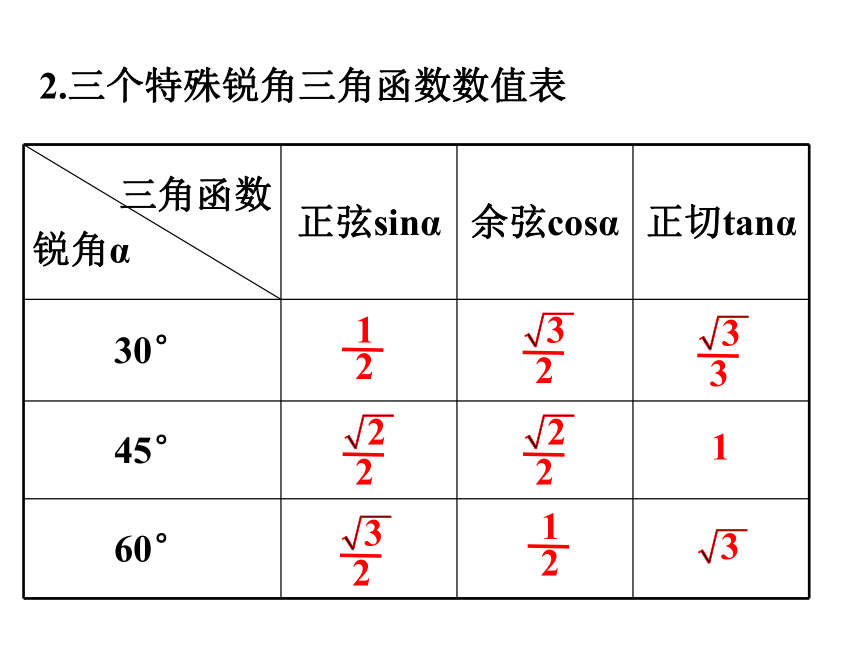
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
1
2
2
3
3
3
2
2
2
2
1
2
3
1
2
3
2.三个特殊锐角三角函数数值表
例1 如图,在 Rt△ABC 中,∠C=90°,AB=10,cos B= ,求 sin B,tan A 的值.
C
A
10
B
3
5
∵cosB=
BC
AB
cosB=
3
5
BC
10
=
3
5
∴BC=6.
∴
∴AC=8.
∴sinB=
AC
AB
=
8
10
=
4
5
tanA=
BC
AC
=
6
8
=
3
4
解:
例题解析
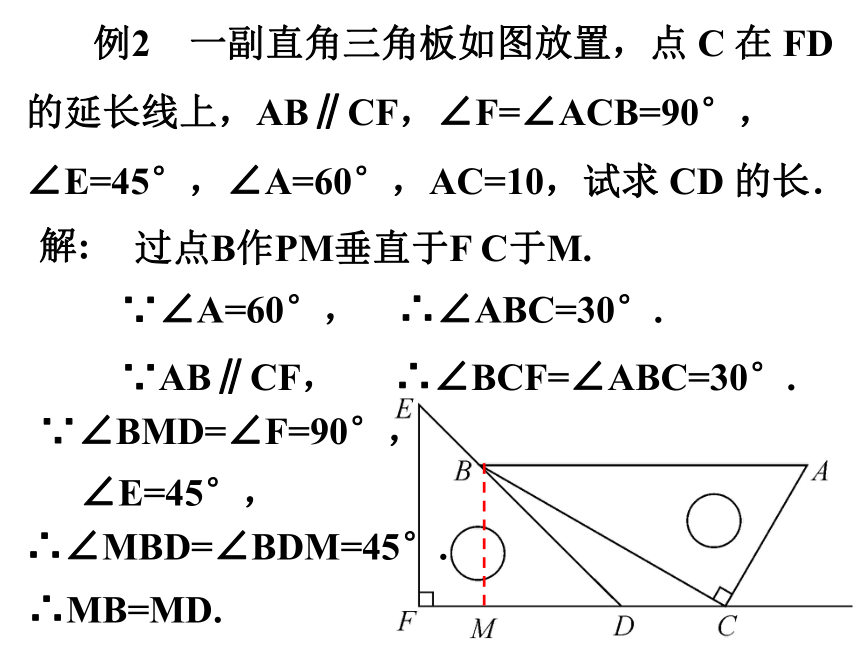
例2 一副直角三角板如图放置,点 C 在 FD 的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求 CD 的长.
解:
过点B作PM垂直于F C于M.
∵∠A=60°,
∴∠ABC=30°.
∵AB∥CF,
∴∠BCF=∠ABC=30°.
∠E=45°,
∵∠BMD=∠F=90°,
∴∠MBD=∠BDM=45°.
∴MB=MD.
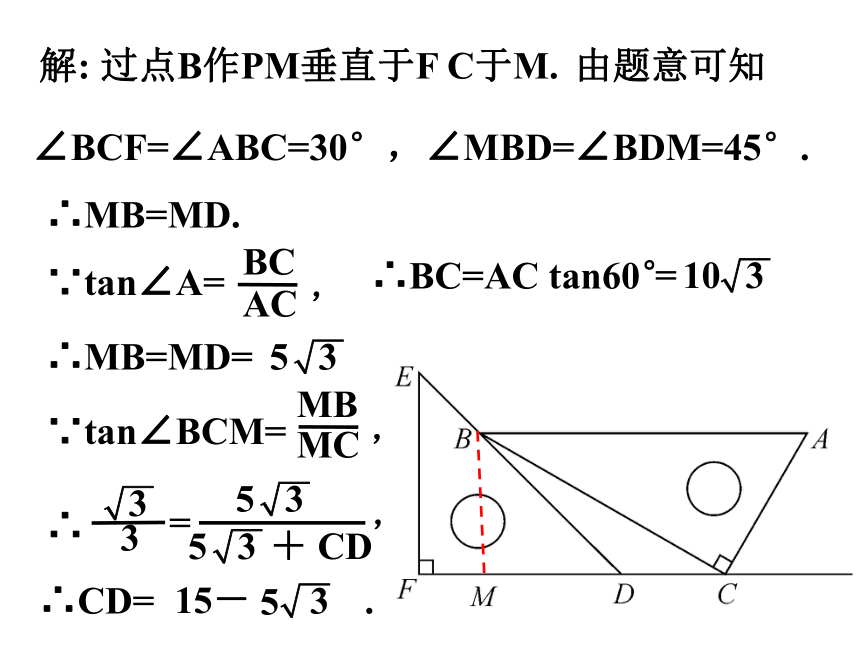
解:
过点B作PM垂直于F C于M.
∠BCF=∠ABC=30°,
∠MBD=∠BDM=45°.
∴MB=MD.
∵tan∠A=
∴BC=AC tan60°
3
10
BC
AC
,
=
∴MB=MD=
3
5
∴CD= .
∵tan∠BCM=
3
3
∴
=
,
3
5
由题意可知
MB
MC
,
+ CD
3
5
3
5
15-
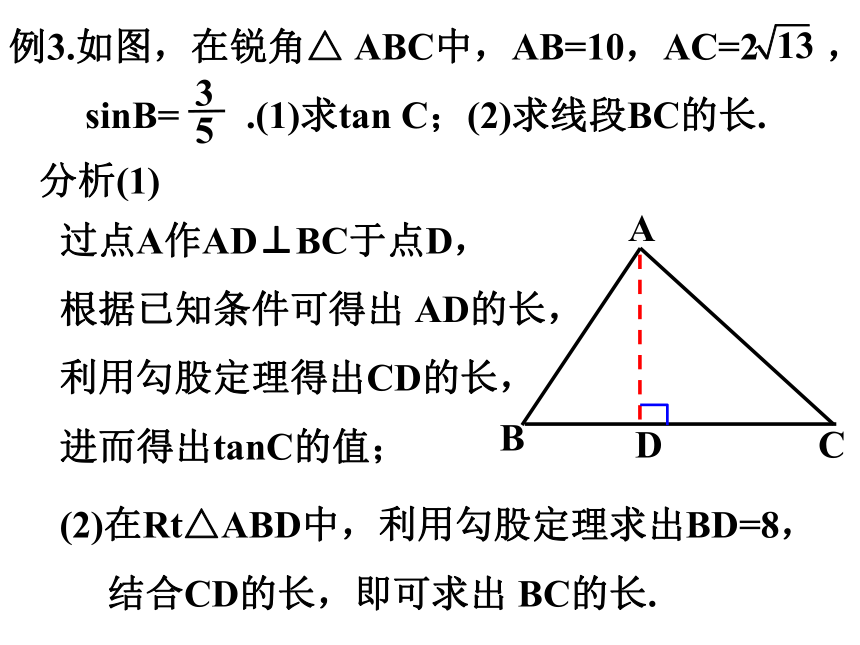
例3.如图,在锐角△ ABC中,AB=10,AC=2 ,
sinB= .(1)求tan C;(2)求线段BC的长.
13
5
3
B
C
A
分析(1)
过点A作AD⊥BC于点D,
根据已知条件可得出 AD的长,
利用勾股定理得出CD的长,
进而得出tanC的值;
(2)在Rt△ABD中,利用勾股定理求出BD=8,
结合CD的长,即可求出 BC的长.
D
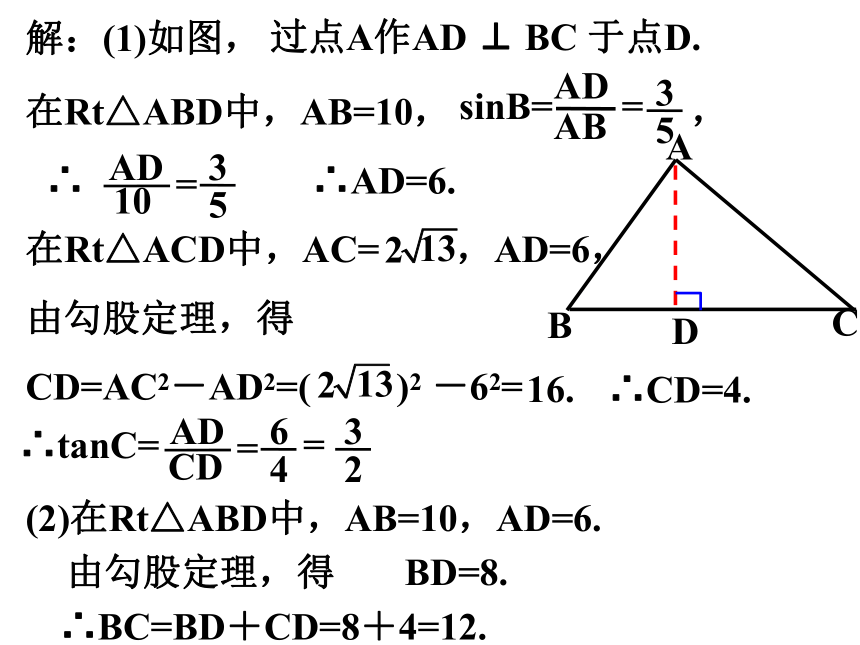
在Rt△ABD中,AB=10, ,
∴AD=6.
在Rt△ACD中,AC= ,AD=6,
由勾股定理,得
CD=AC2-AD2=( )2 -62=
2
13
2
13
16.
解:(1)如图,
∴CD=4.
∴tanC=
CD
AD
B
C
A
过点A作AD ⊥ BC 于点D.
(2)在Rt△ABD中,AB=10,AD=6.
由勾股定理,得
∴BC=BD+CD=8+4=12.
BD=8.
sinB=
AB
AD
=
5
3
=
4
6
=
2
3
D
∴
10
AD
=
5
3
例4.计算: (2sin45°-cos30°)+ -tan230°.
2
24
4
解:原式=
( - )
2
+
2×
2
2
2
3
2
4
6
-
( )2
3
3
=
2
-
2
6
+
2
6
-
1
3
=
5
3
1.在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则cos A= .
B
C
3
A
4
5
4
5
练习巩固
C
B
D
A
6
5
2.如图,在Rt△ABC中,CD是斜边AB上的中线,
已知CD=5,AC=6,则sin A的值是 .
AB=10
4
5
BC=8
3.如图,已知在Rt△ACB中,∠C=90°,AB=13,AC=12,则tan B的值为 .
C
B
13
A
12
5
5
12
A
B
O
4.如图,将∠AOB放置在5×5的正方形网格中,则sin∠AOB的值是( ).
A. B. C. D.
2
3
3
2
13
13
3
13
13
2
C
C
5.将∠BAC放在4×4的正方形方格中,则cos∠BAC的值是 .
A
B
C
5
5
2
6. 在平面直角坐标系内有一点P( 3,4),连接OP,
OP与x轴正方向所夹锐角为α,则sinα= .
x
y
O
P( 3,4)
α
Q
4
5
7. 2tan 45°-2sin 30°= 。
8.2sin 60°-tan 45°-
0
-1
2×
2
3
=
-
| 1- |
3
=
3
-1
-
( -1)
3
=
=
2×1
-
2×
1
2
= .
0
tan60°
| 1- |
3
-1
-
+1
3
=
3
-1
-
=0
9.如图,△ABC中,∠C=90°,AB=8,
cos A= ,则BC的长为 .
3
4
C
A
8
B
∵cosA=
AC
AB
cosA=
3
4
AC
8
=
3
4
∴AC=6
∴
∴BC2=AB2-AC2=82-62=28,
∴BC=
2
7
2
7
12.在Rt△ABC中,∠C=90°,BC=12,
tanB= ,则△ABC的面积为 .
3
4
C
A
12
B
∵tanB=
AC
BC
tanA=
3
4
AC
12
4
3
∴AC=9
∴
=
54
11.如图,在△ABC中,∠C=90°,若∠A=60°,
AC=20 m,则BC大约是( ). (精确到0.1 m)
A.34.64 m B.34.6 m
D.17.3 m
C
B
20
A
C.28.3 m
∵tanA=
BC
AC
∴BC=
20tan60°=
B
20×
3
=20×1.732
13. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE= cm,且tan∠EFC=
(1) △AFB与△FEC有什么关系?
(2)求矩形ABCD的周长.
C
B
A
D
E
F
5
5
3
4
1
3
2
∴△AFB∽△EFC.
(1)△ AFB ∽ △ EFC.
理由如下:
C
B
A
D
E
F
∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△ADE沿BE折叠为△AFE,
∴∠AFE=∠D=90°.
∴∠1+∠2=180°-∠AFE=90°.
∵∠2+∠3=90°,
∴∠1=∠3.
1
3
2
∵tan∠EFC= , tan∠EFC=
∴ =
设EC=3x,
∴EF=5x.
∵DE=EF,
∴AB=DC=DE+EC=EF+EC=8x.
∵∠EFC=∠BAF,
∴tan∠BAF = =
∴BF=6x,
∴AF=10x.
在Rt△AFE中,AE2=AF2+EF2
∴ =(10x)2+(5x)2,
∴x=1,
∴AB=8.
∴ BC=BF+FC=6x+4x=10x=10.
∴L矩形ABCD=2(AB+BC)
=2(10+8)=36.
则 FC=4x,
(2)
EC
FC
3
4
EC
FC
3
4
BF
AB
3
4
C
B
A
D
E
F
( )2
5
5
BF
8x
=
14.如图,在Rt△ABC中, ∠C=90°,D为BC上一点,AB=5,BD=1, tanB= .
(1)求AD的长;
(2) 求sinα的值.
3
4
A
B
C
D
α
在Rt△ABC中,∵∠C=90°,
(1)
tanB=
3
4
tanB=
AC
BC
∴
=
AC
BC
3
4
设AC=3x,
则BC=4x,
∴x=1.
∵AB2=AC2+BC2=(3x)2+(4x)2
∴ AC=3,
BC=4.
∵BD=1,
=52
∴ DC=BC-BD=3
∵AD2=AC2+DC2=32+32
∴ AD=3
2
解:
14.如图,在Rt△ABC中, ∠C=90°,D为BC上一点,AB=5,BD=1, tanB= .
(2) 求sinα的值.
3
4
A
B
C
D
α
解(2):
过点D作DM垂直AB于M.
M
∵∠BMD=∠C=90°,
∠B=∠B,
∴△BDM∽△BAC.
∴ BD:AB=DM:AC.
∴ 1:5=DM:3.
∵AB=5,BD=1,AC=3,
∴ DM= .
3
5
∴ sinα=
DM
AD
=
2
3
3
5
=
10
2
14.如图,在Rt△ABC中, ∠C=90°,D为BC上一点,AB=5,BD=1, tanB= .
(2) 求sinα的值.
3
4
A
B
C
D
α
解(2):
过点B作BM垂直AD,交AD的延长线于M.
M
∵∠BMD=∠C=90°,
∠BDM=∠ADC,
∴△BDM∽△ADC.
∴ BD:AD=BM:AC.
∴ BM= .
∴ sinα=
BM
AB
=
∵AD= ,BD=1,AC=3,
2
3
=
∴ 1: =BM:3.
2
3
5
2
2
2
2
10
2
第23章 解直角三角形 期末复习(1)
锐角三角函数
沪科版
B
a
C
b
A
c
┏
∠A的对边
斜边
∠A的对边
=
a
c
=
=
sinA=
BC
AB
=
cosA=
斜边
∠A的邻边
AC
AB
=
b
c
tanA=
∠ A的邻边
∠A的对边
BC
AC
=
a
b
∠A的邻边
1.锐角三角函数的定义
锐角的正弦、余弦、和正切叫做锐角三角函数.
复习要点
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
1
2
2
3
3
3
2
2
2
2
1
2
3
1
2
3
2.三个特殊锐角三角函数数值表
例1 如图,在 Rt△ABC 中,∠C=90°,AB=10,cos B= ,求 sin B,tan A 的值.
C
A
10
B
3
5
∵cosB=
BC
AB
cosB=
3
5
BC
10
=
3
5
∴BC=6.
∴
∴AC=8.
∴sinB=
AC
AB
=
8
10
=
4
5
tanA=
BC
AC
=
6
8
=
3
4
解:
例题解析
例2 一副直角三角板如图放置,点 C 在 FD 的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求 CD 的长.
解:
过点B作PM垂直于F C于M.
∵∠A=60°,
∴∠ABC=30°.
∵AB∥CF,
∴∠BCF=∠ABC=30°.
∠E=45°,
∵∠BMD=∠F=90°,
∴∠MBD=∠BDM=45°.
∴MB=MD.
解:
过点B作PM垂直于F C于M.
∠BCF=∠ABC=30°,
∠MBD=∠BDM=45°.
∴MB=MD.
∵tan∠A=
∴BC=AC tan60°
3
10
BC
AC
,
=
∴MB=MD=
3
5
∴CD= .
∵tan∠BCM=
3
3
∴
=
,
3
5
由题意可知
MB
MC
,
+ CD
3
5
3
5
15-
例3.如图,在锐角△ ABC中,AB=10,AC=2 ,
sinB= .(1)求tan C;(2)求线段BC的长.
13
5
3
B
C
A
分析(1)
过点A作AD⊥BC于点D,
根据已知条件可得出 AD的长,
利用勾股定理得出CD的长,
进而得出tanC的值;
(2)在Rt△ABD中,利用勾股定理求出BD=8,
结合CD的长,即可求出 BC的长.
D
在Rt△ABD中,AB=10, ,
∴AD=6.
在Rt△ACD中,AC= ,AD=6,
由勾股定理,得
CD=AC2-AD2=( )2 -62=
2
13
2
13
16.
解:(1)如图,
∴CD=4.
∴tanC=
CD
AD
B
C
A
过点A作AD ⊥ BC 于点D.
(2)在Rt△ABD中,AB=10,AD=6.
由勾股定理,得
∴BC=BD+CD=8+4=12.
BD=8.
sinB=
AB
AD
=
5
3
=
4
6
=
2
3
D
∴
10
AD
=
5
3
例4.计算: (2sin45°-cos30°)+ -tan230°.
2
24
4
解:原式=
( - )
2
+
2×
2
2
2
3
2
4
6
-
( )2
3
3
=
2
-
2
6
+
2
6
-
1
3
=
5
3
1.在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则cos A= .
B
C
3
A
4
5
4
5
练习巩固
C
B
D
A
6
5
2.如图,在Rt△ABC中,CD是斜边AB上的中线,
已知CD=5,AC=6,则sin A的值是 .
AB=10
4
5
BC=8
3.如图,已知在Rt△ACB中,∠C=90°,AB=13,AC=12,则tan B的值为 .
C
B
13
A
12
5
5
12
A
B
O
4.如图,将∠AOB放置在5×5的正方形网格中,则sin∠AOB的值是( ).
A. B. C. D.
2
3
3
2
13
13
3
13
13
2
C
C
5.将∠BAC放在4×4的正方形方格中,则cos∠BAC的值是 .
A
B
C
5
5
2
6. 在平面直角坐标系内有一点P( 3,4),连接OP,
OP与x轴正方向所夹锐角为α,则sinα= .
x
y
O
P( 3,4)
α
Q
4
5
7. 2tan 45°-2sin 30°= 。
8.2sin 60°-tan 45°-
0
-1
2×
2
3
=
-
| 1- |
3
=
3
-1
-
( -1)
3
=
=
2×1
-
2×
1
2
= .
0
tan60°
| 1- |
3
-1
-
+1
3
=
3
-1
-
=0
9.如图,△ABC中,∠C=90°,AB=8,
cos A= ,则BC的长为 .
3
4
C
A
8
B
∵cosA=
AC
AB
cosA=
3
4
AC
8
=
3
4
∴AC=6
∴
∴BC2=AB2-AC2=82-62=28,
∴BC=
2
7
2
7
12.在Rt△ABC中,∠C=90°,BC=12,
tanB= ,则△ABC的面积为 .
3
4
C
A
12
B
∵tanB=
AC
BC
tanA=
3
4
AC
12
4
3
∴AC=9
∴
=
54
11.如图,在△ABC中,∠C=90°,若∠A=60°,
AC=20 m,则BC大约是( ). (精确到0.1 m)
A.34.64 m B.34.6 m
D.17.3 m
C
B
20
A
C.28.3 m
∵tanA=
BC
AC
∴BC=
20tan60°=
B
20×
3
=20×1.732
13. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE= cm,且tan∠EFC=
(1) △AFB与△FEC有什么关系?
(2)求矩形ABCD的周长.
C
B
A
D
E
F
5
5
3
4
1
3
2
∴△AFB∽△EFC.
(1)△ AFB ∽ △ EFC.
理由如下:
C
B
A
D
E
F
∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△ADE沿BE折叠为△AFE,
∴∠AFE=∠D=90°.
∴∠1+∠2=180°-∠AFE=90°.
∵∠2+∠3=90°,
∴∠1=∠3.
1
3
2
∵tan∠EFC= , tan∠EFC=
∴ =
设EC=3x,
∴EF=5x.
∵DE=EF,
∴AB=DC=DE+EC=EF+EC=8x.
∵∠EFC=∠BAF,
∴tan∠BAF = =
∴BF=6x,
∴AF=10x.
在Rt△AFE中,AE2=AF2+EF2
∴ =(10x)2+(5x)2,
∴x=1,
∴AB=8.
∴ BC=BF+FC=6x+4x=10x=10.
∴L矩形ABCD=2(AB+BC)
=2(10+8)=36.
则 FC=4x,
(2)
EC
FC
3
4
EC
FC
3
4
BF
AB
3
4
C
B
A
D
E
F
( )2
5
5
BF
8x
=
14.如图,在Rt△ABC中, ∠C=90°,D为BC上一点,AB=5,BD=1, tanB= .
(1)求AD的长;
(2) 求sinα的值.
3
4
A
B
C
D
α
在Rt△ABC中,∵∠C=90°,
(1)
tanB=
3
4
tanB=
AC
BC
∴
=
AC
BC
3
4
设AC=3x,
则BC=4x,
∴x=1.
∵AB2=AC2+BC2=(3x)2+(4x)2
∴ AC=3,
BC=4.
∵BD=1,
=52
∴ DC=BC-BD=3
∵AD2=AC2+DC2=32+32
∴ AD=3
2
解:
14.如图,在Rt△ABC中, ∠C=90°,D为BC上一点,AB=5,BD=1, tanB= .
(2) 求sinα的值.
3
4
A
B
C
D
α
解(2):
过点D作DM垂直AB于M.
M
∵∠BMD=∠C=90°,
∠B=∠B,
∴△BDM∽△BAC.
∴ BD:AB=DM:AC.
∴ 1:5=DM:3.
∵AB=5,BD=1,AC=3,
∴ DM= .
3
5
∴ sinα=
DM
AD
=
2
3
3
5
=
10
2
14.如图,在Rt△ABC中, ∠C=90°,D为BC上一点,AB=5,BD=1, tanB= .
(2) 求sinα的值.
3
4
A
B
C
D
α
解(2):
过点B作BM垂直AD,交AD的延长线于M.
M
∵∠BMD=∠C=90°,
∠BDM=∠ADC,
∴△BDM∽△ADC.
∴ BD:AD=BM:AC.
∴ BM= .
∴ sinα=
BM
AB
=
∵AD= ,BD=1,AC=3,
2
3
=
∴ 1: =BM:3.
2
3
5
2
2
2
2
10
2
