第23章 解直角三角形 期末复习(2) 课件(共25张PPT)
文档属性
| 名称 | 第23章 解直角三角形 期末复习(2) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 16:02:21 | ||
图片预览





文档简介
(共25张PPT)
第23章 解直角三角形 期末复习(2)
解直角三角形的应用
沪科版
(1)三边之间的关系
A
C
B
c
a
b
1.直角三角形各元素之间的关系
a2+b2=c2
(勾股定理)
(2)两锐角之间的关系
(3)边角之间的关系
∠A+∠B=90°
sin A= ,cos A= ,tan A= ,
sin B= ,cos B= ,tan B= .
a
c
b
c
a
b
a
c
b
c
b
a
复习要点
2.锐角三角函数实际应用中的相关概念
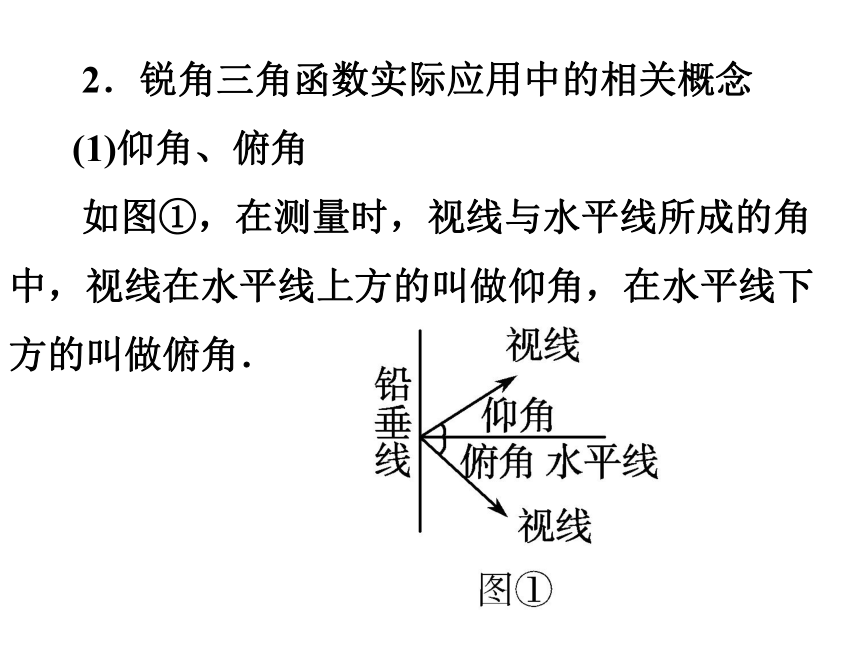
(1)仰角、俯角
如图①,在测量时,视线与水平线所成的角中,视线在水平线上方的叫做仰角,在水平线下方的叫做俯角.
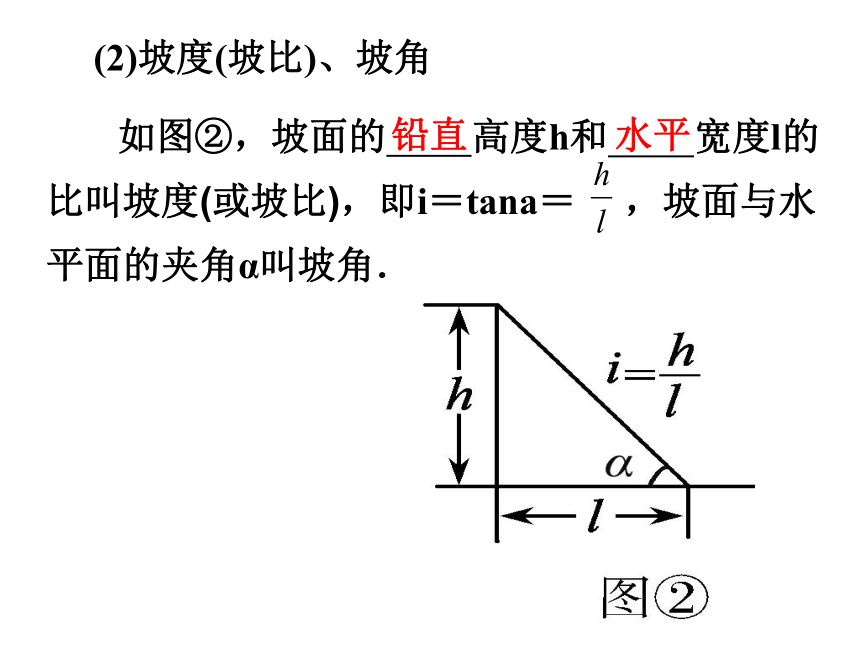
如图②,坡面的 高度h和 宽度l的比叫坡度(或坡比),即i=tana= ,坡面与水平面的夹角α叫坡角.
(2)坡度(坡比)、坡角
铅直
水平
例1 已知,如图,在△ABC 中,∠ACB=90°,CD⊥AB,垂足为 D,若∠B=30°,CD=6,求 AB 的长.
A
C
D
B
解:
∵∠ACB=90°,
∠B=30°,
∴∠A=60°.
∵CD⊥AB,
∴∠CDB=∠CDA=90°,
∴∠ACD=30°,
∴∠BCD=60°.
∵tan∠ACD= ,
tan∠BCD= .
∴AD=CDtan30°= ,
BD=CDtan60°= ,
∴AB=AD+BD
= +
2
3
6
3
2
3
6
3
= .
8
3
CD
AD
CD
BD
例题解析
例2 如图,小明同学在民族广场A处放风筝,风筝位于B处,风筝线 AB长为100m,从A处看风筝的仰角为30°,小明的父母从C处看风筝的仰角为50°.
(1)风筝离地面多少米
(2)A,C相距多少米 (结果保留小数点后一位,参考数据:sin30=0. 5, cos30°≈0.8660,tan30° ≈0.5774,sin50°≈0.7760,cos50°≈0.6428,tan50°≈1.1918)
A
C
B
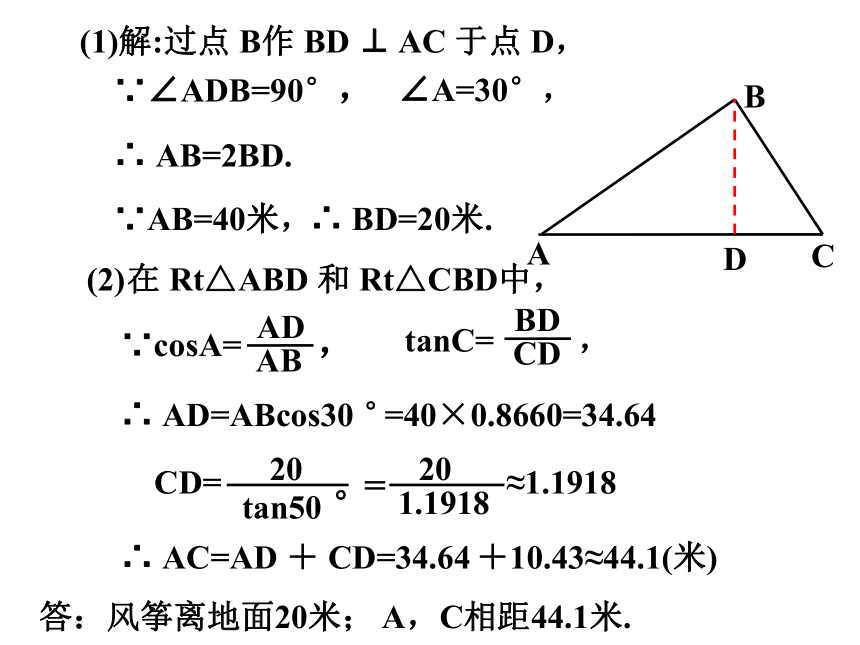
(1)解:过点 B作 BD ⊥ AC 于点 D,
A
C
B
D
∵∠ADB=90°,
∠A=30°,
∴ AB=2BD.
∵AB=40米,
∴ BD=20米.
答:风筝离地面20米; A,C相距44.1米.
(2)
在 Rt△ABD 和 Rt△CBD中,
∵cosA= ,
tanC= ,
AB
AD
CD
BD
∴ AD=ABcos30 °
=40×0.8660=34.64
CD=
tan50 °
20
=
1.1918
20
≈1.1918
∴ AC=AD + CD=34.64 +10.43≈44.1(米)
B
A
C
30°
北
15°
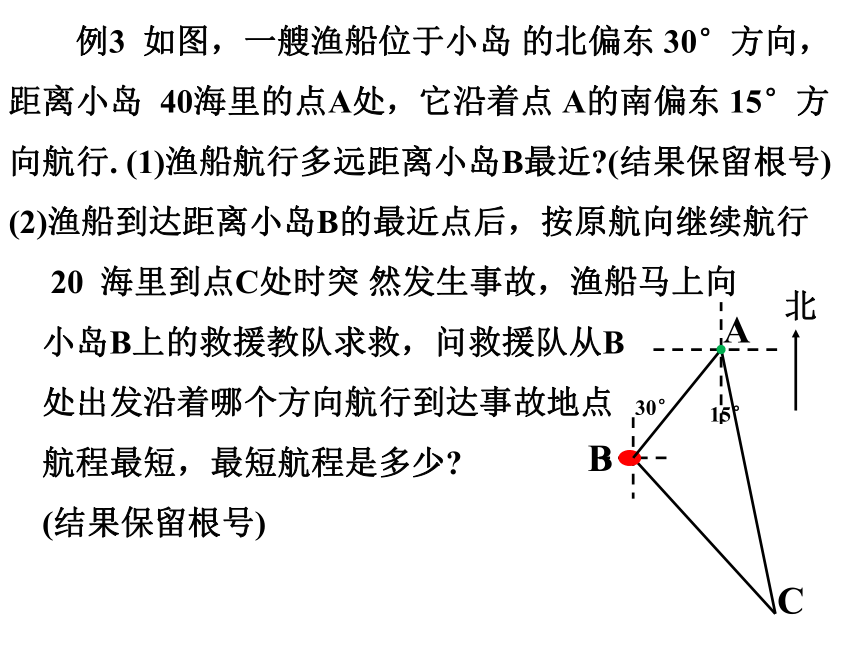
例3 如图,一艘渔船位于小岛 的北偏东 30°方向,距离小岛 40海里的点A处,它沿着点 A的南偏东 15°方向航行. (1)渔船航行多远距离小岛B最近 (结果保留根号)
(2)渔船到达距离小岛B的最近点后,按原航向继续航行
20 海里到点C处时突 然发生事故,渔船马上向
小岛B上的救援教队求救,问救援队从B
处出发沿着哪个方向航行到达事故地点
航程最短,最短航程是多少
(结果保留根号)
解:(1)过点 B作 BM ⊥ AC 于点M,
由题意知∠ BAM= 45° ,
则 ∠ABM=45°
在 Rt△ABM 中,
AM=ABsin ∠ABM=AB sin45 ° .
∵AB=40,
答:渔船航行 20 海里距离小岛B最近.
∴ AM=
40×
=20
2
2
2
2
B
A
C
30°
北
15°
M
(2) ∵ BM= 20 √2 海里,MC= 20 √6 海里,
∴ tan ∠ MBC=
∴ ∠ MBC=60°
∴ ∠CBG=180 °-60 °
- 45° - 30°=45°.
在Rt△BCM中, ∵∠ CBM=60°,
∴BC=2BM=40√2 (海里).
答:救援队从B处出发沿着点B的南偏东 45°方向航行到达事故地点航程最短,最短航程是40√2 海里.
B
A
C
30°
北
15°
M
∴ ∠C=30°.
BM
MC
=
20 √6
20 √2
=
3
例4 如图,已知斜坡 AB长为80米,坡角为30°,现计划在斜坡中点D处挖去部分坡体(用阴影表示),修建一个平行于水平线 CA的平台 DE 和一条新的斜坡BE.若修建的斜坡 BE的坡角为45°,求平台 DE 的长.
∵修建的斜坡 BE的坡角为45°,
解:
∴ ∠BEF=45°.
A
B
C
D
E
F
∵ ∠DAC=∠BDF=30°,
AD=BD=40米,
∴ BF=EF= BD=20米.
DF=
∴ DE=DF-EF=( -20)米
答:平台 DE 的长为(20 -20)米.
20
3
20
3
3
1
2
例5 城市规划期间,欲拆除一电线杆 AB,已知距电线杆 AB 水平距离 14 m 的 D 处有一大坝,背水坡 CD的坡度 i =2∶1,坝高 CF 为 2 m,在坝顶 C 处测得杆顶 A 的仰角为 30°,D,E 之间是宽为 2 m 的人行道.试问:在拆除电线杆 AB 时,为确保行人安全,是否需要将此人行道封上?
A
B
G
C
E D
F
30°
人行道
A
B
G
C
E D
F
30°
人行道
解:
∵背水坡 CD的坡度 i =2∶1,坝高 CF 为 2 m,
∴ DF 为 1 m,
∴BF=BD+DF=14+1=15(m)
∴BE=BF-DF - DE=15 -1-2=12(m)
∵四边形BFCG是矩形,
∴CG=BF=15,
BG=CF=2.
在Rt△AGC中,
tan C=
CG
AG
∴ AG=CG tan30 °
∴ AB=AG+BG
=15×
3
3
=5
3
=5
3
+2
≈10.6(m)
∴不需要将此人行道封上.
<12(m)
1.如图,某景区有一处索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,则山峰AD的高度为 米.
(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
A
B
C
D
480
练习巩固
(结果精确到1米)
2.某市跨江大桥即将竣工,某学生做了一个平面示意图(如图).点A到桥的距离是40米,测得∠A=83°,则大桥BC的长度是 米.
(参考数据:sin83°≈0.99,
cos83°≈0.12,
tan83°≈8.14.)
A
B
C
326
3.某学校兴趣小组开展实践活动,通过观测数据,计算气球升空的高度 AB.如图,在平面内,点B,C,D在同一直线上,AB⊥CB,垂足为点B, ∠ACB=52°, ∠ ADB=60°, CD=200m.则AB的高度为 m.
(精确到1m)(参考数据:sin52° ≈ 0.79,cos52°≈ 0.62,
tan 52°≈1.28 , ≈ 1.73)
3
60°
A
B
C
D
52°
984
4.海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D= .
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,
求sin∠BCF的值.
A
B
C
D
E
F
3
5
练习巩固
解:(1)在Rt△CDE中,
(海里) .
A
B
C
D
E
F
∵ cos∠D =
DE
CD
∴
DE=30,
cos∠D =
3
5
30
CD
=
3
5
∴CD=50
∴BE= CD
∵B点是CD的中点,
1
2
=25
∴AB=
BE-AE
=25-8.3
=18.7
(2)在Rt△CDE中,由勾股定理得
A
B
C
D
E
F
∴BE= CD
1
2
=BC
∴∠BEC=∠BCE
∴cos∠BEC=cos∠BCE
∴
EF
EC
=
EC
CD
∴EF=
EC2
CD
=
402
50
=32
∴BF=
EF-BE
=32-25
=7
∴sin∠BCF =
BF
BC
=
7
25
EC2=
CD2-DE2
=502-302
∴EC=40.
=402,
要求BF
要求EF
要求CE
5.如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡脚到楼房的距离CB=8m.在D点处观察楼顶A点的仰角为54°,坡角∠DCE=30 .求楼房AB的高. (结果精确到0.1m).( , , , . )
E
A
B
C
D
30
54°
解:过D点作DF⊥AB,交AB于点F.
在Rt△ECD中,CD=6,∠ECD=30°,
∴DE=3=FB,
∴DF=CB+EC
在Rt△ADF中,tan∠ADF= ,
∴AF=DF×tan54°.
∴AF= ×1.38
∴AB=
∴楼房AB的高度约是21.2m.
3
3
=8+ .
3
3
AF
DF
≈18.20.
(8+ )
3
3
E
A
B
C
D
30°
F
EC=
AF+FB
=18.20+3=21.20
≈21.2.
54°
3.如图,大楼外墙有高为AB 的广告牌,由距离大楼20 米的点 C(即CD=20米)观察它的顶部 A的仰角是55° ,底部B 的仰角是42° .求 AB的高度.参考数据:
C
D
B
A
sin55° ≈0.82,cos55° ≈0.57,tan55° ≈1.43;
sin42° ≈0.67,cos42° ≈0.74,tan42° ≈0.90.
6.如图,大楼外墙有高为AB 的广告牌,由距离大楼20 米的点 C(即CD=20米)观察它的顶部 A的仰角是55° ,底部B 的仰角是42° .求 AB的高度.参考数据:
C
D
B
A
sin55° ≈0.82,cos55° ≈0.57,tan55° ≈1.43;
sin42° ≈0.67,cos42° ≈0.74,tan42° ≈0.90.
在Rt△ACD中,
∵ tan∠ACD =
AD
CD
∴AD=CD×tan55°
在Rt△BCD中,
∵ tan∠BCD =
BD
CD
∴BD=CD×tan42°
∴AB=
AD-BD
C
D
B
A
sin55° ≈0.82,cos55° ≈0.57,tan55° ≈1.43;
sin42° ≈0.67,cos42° ≈0.74,tan42° ≈0.90.
在Rt△ACD中,
∵ tan∠ACD =
AD
CD
∴AD=CD×tan55°
在Rt△BCD中,
∵ tan∠BCD =
BD
CD
∴BD=CD×tan42°
∴AB=
AD-BD
=CD×tan55°
-CD×tan42°
=CD(tan55°-tan42°)
≈20×(1.43-0.90)
=10.6(m).
第23章 解直角三角形 期末复习(2)
解直角三角形的应用
沪科版
(1)三边之间的关系
A
C
B
c
a
b
1.直角三角形各元素之间的关系
a2+b2=c2
(勾股定理)
(2)两锐角之间的关系
(3)边角之间的关系
∠A+∠B=90°
sin A= ,cos A= ,tan A= ,
sin B= ,cos B= ,tan B= .
a
c
b
c
a
b
a
c
b
c
b
a
复习要点
2.锐角三角函数实际应用中的相关概念
(1)仰角、俯角
如图①,在测量时,视线与水平线所成的角中,视线在水平线上方的叫做仰角,在水平线下方的叫做俯角.
如图②,坡面的 高度h和 宽度l的比叫坡度(或坡比),即i=tana= ,坡面与水平面的夹角α叫坡角.
(2)坡度(坡比)、坡角
铅直
水平
例1 已知,如图,在△ABC 中,∠ACB=90°,CD⊥AB,垂足为 D,若∠B=30°,CD=6,求 AB 的长.
A
C
D
B
解:
∵∠ACB=90°,
∠B=30°,
∴∠A=60°.
∵CD⊥AB,
∴∠CDB=∠CDA=90°,
∴∠ACD=30°,
∴∠BCD=60°.
∵tan∠ACD= ,
tan∠BCD= .
∴AD=CDtan30°= ,
BD=CDtan60°= ,
∴AB=AD+BD
= +
2
3
6
3
2
3
6
3
= .
8
3
CD
AD
CD
BD
例题解析
例2 如图,小明同学在民族广场A处放风筝,风筝位于B处,风筝线 AB长为100m,从A处看风筝的仰角为30°,小明的父母从C处看风筝的仰角为50°.
(1)风筝离地面多少米
(2)A,C相距多少米 (结果保留小数点后一位,参考数据:sin30=0. 5, cos30°≈0.8660,tan30° ≈0.5774,sin50°≈0.7760,cos50°≈0.6428,tan50°≈1.1918)
A
C
B
(1)解:过点 B作 BD ⊥ AC 于点 D,
A
C
B
D
∵∠ADB=90°,
∠A=30°,
∴ AB=2BD.
∵AB=40米,
∴ BD=20米.
答:风筝离地面20米; A,C相距44.1米.
(2)
在 Rt△ABD 和 Rt△CBD中,
∵cosA= ,
tanC= ,
AB
AD
CD
BD
∴ AD=ABcos30 °
=40×0.8660=34.64
CD=
tan50 °
20
=
1.1918
20
≈1.1918
∴ AC=AD + CD=34.64 +10.43≈44.1(米)
B
A
C
30°
北
15°
例3 如图,一艘渔船位于小岛 的北偏东 30°方向,距离小岛 40海里的点A处,它沿着点 A的南偏东 15°方向航行. (1)渔船航行多远距离小岛B最近 (结果保留根号)
(2)渔船到达距离小岛B的最近点后,按原航向继续航行
20 海里到点C处时突 然发生事故,渔船马上向
小岛B上的救援教队求救,问救援队从B
处出发沿着哪个方向航行到达事故地点
航程最短,最短航程是多少
(结果保留根号)
解:(1)过点 B作 BM ⊥ AC 于点M,
由题意知∠ BAM= 45° ,
则 ∠ABM=45°
在 Rt△ABM 中,
AM=ABsin ∠ABM=AB sin45 ° .
∵AB=40,
答:渔船航行 20 海里距离小岛B最近.
∴ AM=
40×
=20
2
2
2
2
B
A
C
30°
北
15°
M
(2) ∵ BM= 20 √2 海里,MC= 20 √6 海里,
∴ tan ∠ MBC=
∴ ∠ MBC=60°
∴ ∠CBG=180 °-60 °
- 45° - 30°=45°.
在Rt△BCM中, ∵∠ CBM=60°,
∴BC=2BM=40√2 (海里).
答:救援队从B处出发沿着点B的南偏东 45°方向航行到达事故地点航程最短,最短航程是40√2 海里.
B
A
C
30°
北
15°
M
∴ ∠C=30°.
BM
MC
=
20 √6
20 √2
=
3
例4 如图,已知斜坡 AB长为80米,坡角为30°,现计划在斜坡中点D处挖去部分坡体(用阴影表示),修建一个平行于水平线 CA的平台 DE 和一条新的斜坡BE.若修建的斜坡 BE的坡角为45°,求平台 DE 的长.
∵修建的斜坡 BE的坡角为45°,
解:
∴ ∠BEF=45°.
A
B
C
D
E
F
∵ ∠DAC=∠BDF=30°,
AD=BD=40米,
∴ BF=EF= BD=20米.
DF=
∴ DE=DF-EF=( -20)米
答:平台 DE 的长为(20 -20)米.
20
3
20
3
3
1
2
例5 城市规划期间,欲拆除一电线杆 AB,已知距电线杆 AB 水平距离 14 m 的 D 处有一大坝,背水坡 CD的坡度 i =2∶1,坝高 CF 为 2 m,在坝顶 C 处测得杆顶 A 的仰角为 30°,D,E 之间是宽为 2 m 的人行道.试问:在拆除电线杆 AB 时,为确保行人安全,是否需要将此人行道封上?
A
B
G
C
E D
F
30°
人行道
A
B
G
C
E D
F
30°
人行道
解:
∵背水坡 CD的坡度 i =2∶1,坝高 CF 为 2 m,
∴ DF 为 1 m,
∴BF=BD+DF=14+1=15(m)
∴BE=BF-DF - DE=15 -1-2=12(m)
∵四边形BFCG是矩形,
∴CG=BF=15,
BG=CF=2.
在Rt△AGC中,
tan C=
CG
AG
∴ AG=CG tan30 °
∴ AB=AG+BG
=15×
3
3
=5
3
=5
3
+2
≈10.6(m)
∴不需要将此人行道封上.
<12(m)
1.如图,某景区有一处索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,则山峰AD的高度为 米.
(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
A
B
C
D
480
练习巩固
(结果精确到1米)
2.某市跨江大桥即将竣工,某学生做了一个平面示意图(如图).点A到桥的距离是40米,测得∠A=83°,则大桥BC的长度是 米.
(参考数据:sin83°≈0.99,
cos83°≈0.12,
tan83°≈8.14.)
A
B
C
326
3.某学校兴趣小组开展实践活动,通过观测数据,计算气球升空的高度 AB.如图,在平面内,点B,C,D在同一直线上,AB⊥CB,垂足为点B, ∠ACB=52°, ∠ ADB=60°, CD=200m.则AB的高度为 m.
(精确到1m)(参考数据:sin52° ≈ 0.79,cos52°≈ 0.62,
tan 52°≈1.28 , ≈ 1.73)
3
60°
A
B
C
D
52°
984
4.海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D= .
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,
求sin∠BCF的值.
A
B
C
D
E
F
3
5
练习巩固
解:(1)在Rt△CDE中,
(海里) .
A
B
C
D
E
F
∵ cos∠D =
DE
CD
∴
DE=30,
cos∠D =
3
5
30
CD
=
3
5
∴CD=50
∴BE= CD
∵B点是CD的中点,
1
2
=25
∴AB=
BE-AE
=25-8.3
=18.7
(2)在Rt△CDE中,由勾股定理得
A
B
C
D
E
F
∴BE= CD
1
2
=BC
∴∠BEC=∠BCE
∴cos∠BEC=cos∠BCE
∴
EF
EC
=
EC
CD
∴EF=
EC2
CD
=
402
50
=32
∴BF=
EF-BE
=32-25
=7
∴sin∠BCF =
BF
BC
=
7
25
EC2=
CD2-DE2
=502-302
∴EC=40.
=402,
要求BF
要求EF
要求CE
5.如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡脚到楼房的距离CB=8m.在D点处观察楼顶A点的仰角为54°,坡角∠DCE=30 .求楼房AB的高. (结果精确到0.1m).( , , , . )
E
A
B
C
D
30
54°
解:过D点作DF⊥AB,交AB于点F.
在Rt△ECD中,CD=6,∠ECD=30°,
∴DE=3=FB,
∴DF=CB+EC
在Rt△ADF中,tan∠ADF= ,
∴AF=DF×tan54°.
∴AF= ×1.38
∴AB=
∴楼房AB的高度约是21.2m.
3
3
=8+ .
3
3
AF
DF
≈18.20.
(8+ )
3
3
E
A
B
C
D
30°
F
EC=
AF+FB
=18.20+3=21.20
≈21.2.
54°
3.如图,大楼外墙有高为AB 的广告牌,由距离大楼20 米的点 C(即CD=20米)观察它的顶部 A的仰角是55° ,底部B 的仰角是42° .求 AB的高度.参考数据:
C
D
B
A
sin55° ≈0.82,cos55° ≈0.57,tan55° ≈1.43;
sin42° ≈0.67,cos42° ≈0.74,tan42° ≈0.90.
6.如图,大楼外墙有高为AB 的广告牌,由距离大楼20 米的点 C(即CD=20米)观察它的顶部 A的仰角是55° ,底部B 的仰角是42° .求 AB的高度.参考数据:
C
D
B
A
sin55° ≈0.82,cos55° ≈0.57,tan55° ≈1.43;
sin42° ≈0.67,cos42° ≈0.74,tan42° ≈0.90.
在Rt△ACD中,
∵ tan∠ACD =
AD
CD
∴AD=CD×tan55°
在Rt△BCD中,
∵ tan∠BCD =
BD
CD
∴BD=CD×tan42°
∴AB=
AD-BD
C
D
B
A
sin55° ≈0.82,cos55° ≈0.57,tan55° ≈1.43;
sin42° ≈0.67,cos42° ≈0.74,tan42° ≈0.90.
在Rt△ACD中,
∵ tan∠ACD =
AD
CD
∴AD=CD×tan55°
在Rt△BCD中,
∵ tan∠BCD =
BD
CD
∴BD=CD×tan42°
∴AB=
AD-BD
=CD×tan55°
-CD×tan42°
=CD(tan55°-tan42°)
≈20×(1.43-0.90)
=10.6(m).
