第21章二次函数与反比例函数期末复习(3)二次函数的图象信息 课件(共25张PPT)
文档属性
| 名称 | 第21章二次函数与反比例函数期末复习(3)二次函数的图象信息 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 00:00:00 | ||
图片预览


文档简介
(共25张PPT)
第21章 二次函数与反比例函数期末复习(3)
二次函数系数符号与图象的信息
沪科版
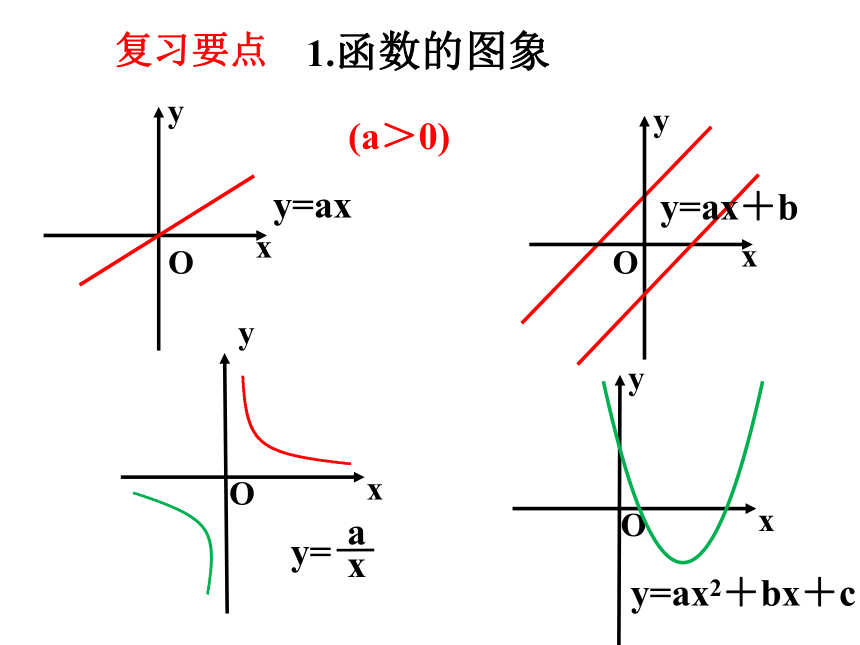
1.函数的图象
x
y
O
x
y
O
x
y
O
x
y
O
y=ax
(a>0)
y=ax+b
y=ax2+bx+c
y=
a
x
复习要点
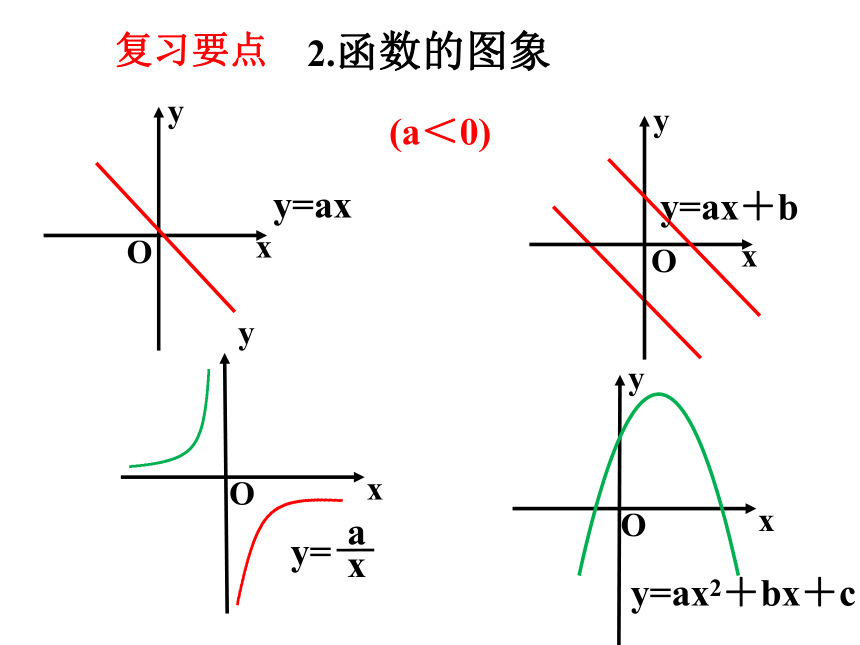
2.函数的图象
x
y
O
x
y
O
x
y
O
x
y
O
y=ax
(a<0)
y=ax+b
y=ax2+bx+c
y=
a
x
复习要点
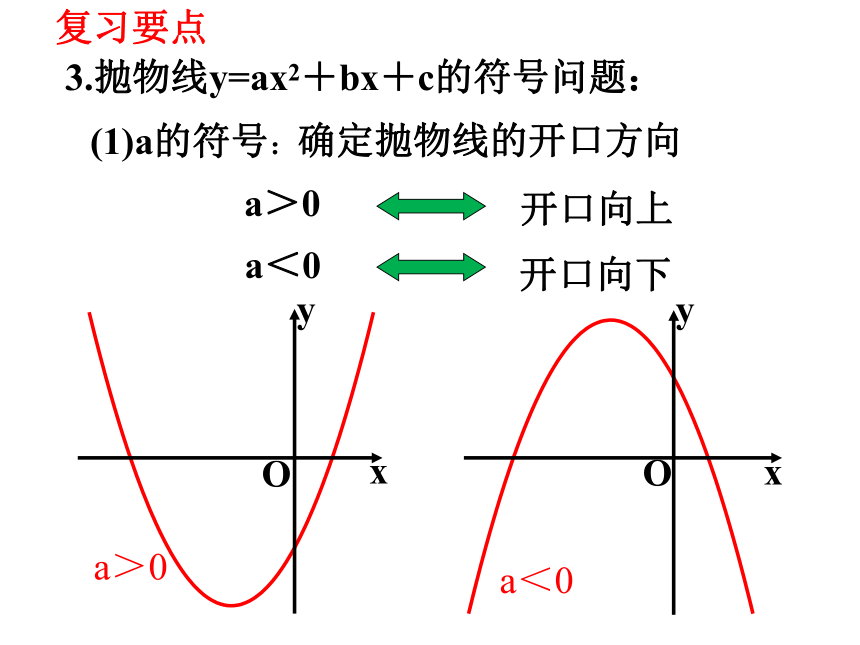
3.抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
确定抛物线的开口方向
开口向上
a>0
开口向下
a<0
x
y
O
x
y
O
a>0
a<0
复习要点
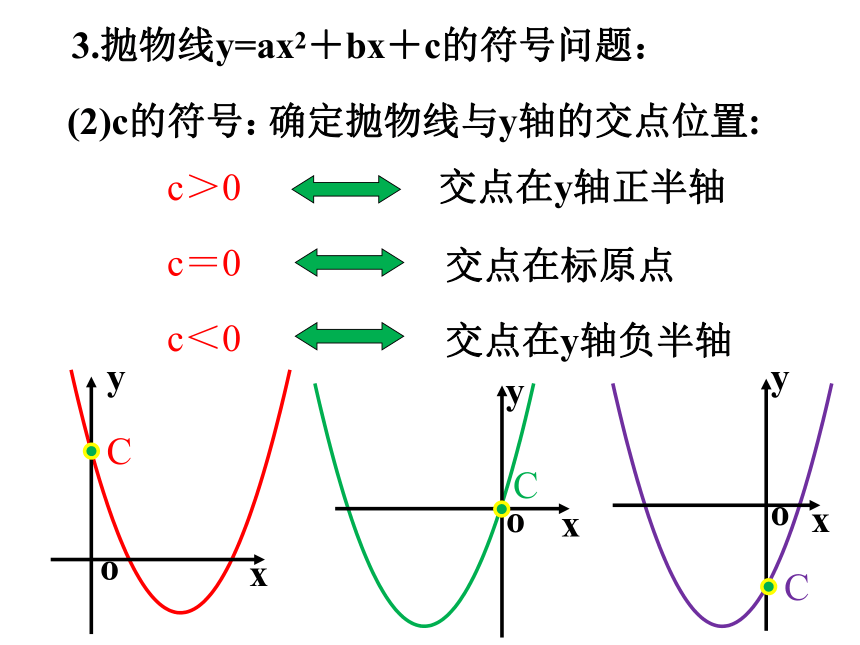
3.抛物线y=ax2+bx+c的符号问题:
(2)c的符号:
确定抛物线与y轴的交点位置:
交点在y轴正半轴
c>0
交点在y轴负半轴
c<0
交点在标原点
c=0
x
y
o
x
y
o
x
y
o
C
C
C
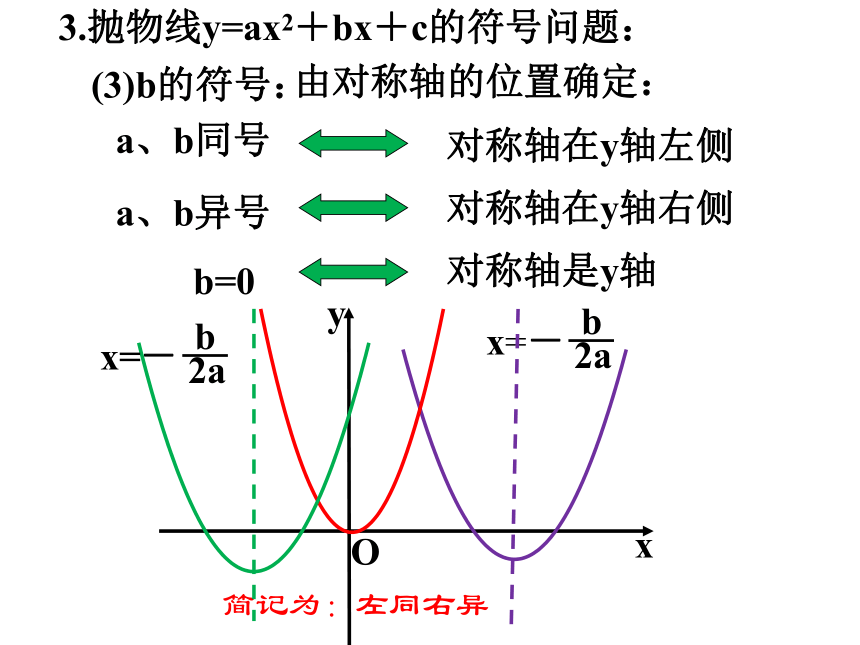
(3)b的符号:
由对称轴的位置确定:
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
简记为:左同右异
x
y
O
b
2a
-
x=
b
2a
-
x=
3.抛物线y=ax2+bx+c的符号问题:
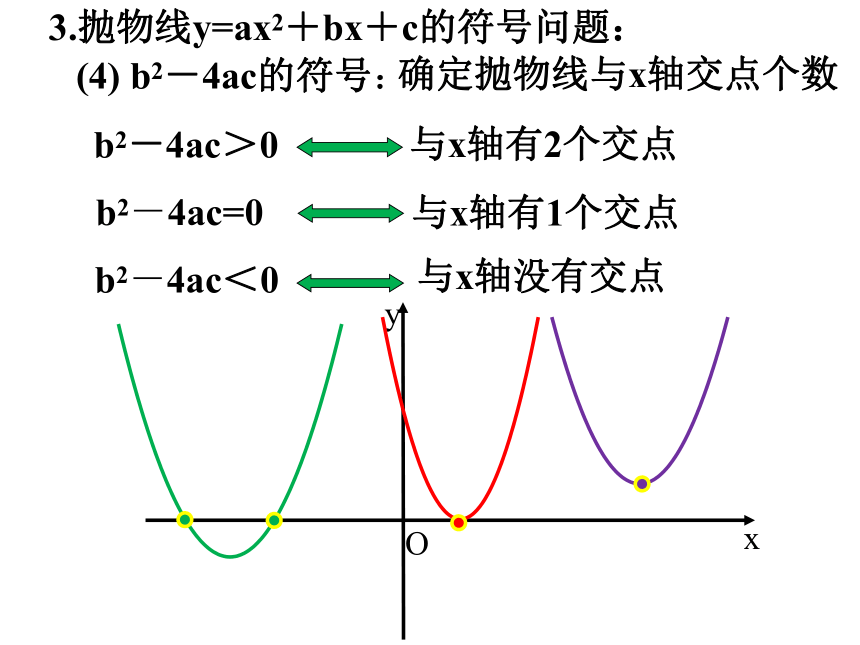
(4) b2-4ac的符号:
确定抛物线与x轴交点个数
x
y
O
与x轴有2个交点
与x轴有1个交点
与x轴没有交点
b2-4ac>0
b2-4ac=0
b2-4ac<0
3.抛物线y=ax2+bx+c的符号问题:
2a-b
2a+b
a+b+c
a-b+c
4a+2b+c
4a-2b+c
b
2a
-
常与1比较
>1;
<1;
=1.
b
2a
-
常与1比较
>1;
<1;
=1.
x=1的函数值
>0,在x轴的上方
<0,在x轴的下方
x=-1的函数值
>0,在x轴的上方
<0,在x轴的下方
x=2的函数值
>0,在x轴的上方
<0,在x轴的下方
x=-2的函数值
>0,在x轴的上方
<0,在x轴的下方
复习要点
4.常见代数式的意义及其作用
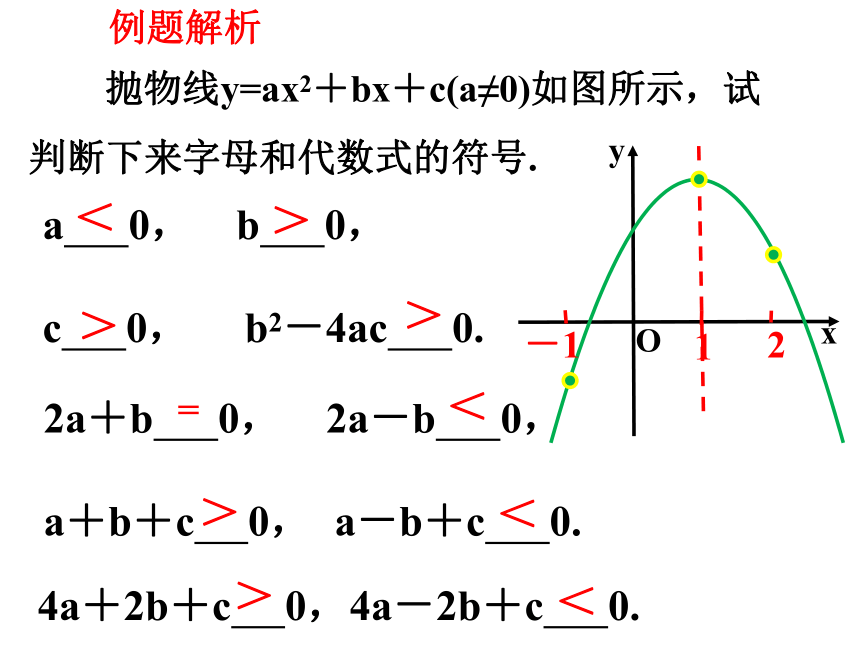
抛物线y=ax2+bx+c(a≠0)如图所示,试
判断下来字母和代数式的符号.
a 0, b 0,
c 0, b2-4ac 0.
2a+b 0, 2a-b 0,
a+b+c 0, a-b+c 0.
4a+2b+c 0,4a-2b+c 0.
x
y
O
1
2
-1
<
>
>
>
=
<
>
<
>
<
例题解析
1.抛物线y=ax2+bx+c(a≠0)的图象如图所示,
则下列a、b、c间关系判断正确的是( ).
x
y
O
A . ab<0
C. a+b+c>0
B . bc<0
D.a-b+c<0;
练习巩固
D
2.已知一次函数y=ax-c的图象经过二、一、四象限,则二次函数y=ax2+c大致图象可能是( ).
A .
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
D
3.在同一直角坐标系中,二次函数y=ax2+bx
与一次函数y=ax+b的大致图象可能是( ).
A .
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
a>0
a>0
b>0
b=0
a>0
b>0
a>0
b>0
a>0
b<0
a<0
b<0
a>0
b>0
a>0
b<0
C
c=0
4.在同一直角坐标系中,二次函数y=ax2+bx +c与一次函数y=ax+c的大致图象可能是( ).
A .
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
a>0
c<0
a<0
c>0
a<0
a<0
c>0
c>0
a>0
c>0
c<0
a>0
a<0
c>0
a>0
c>0
B
5. 如图,二次函数y=ax2-a和反比例函数
y= 在同一直角坐标系中的图象可能是( ).
A .
B.
C.
D.
a
x
x
y
O
x
y
O
x
y
O
x
y
O
a<0
-a>0
a>0
a>0
-a<0
a>0
a<0
a<0
-a>0
a<0
a<0
-a<0
D
6.已知二次函数y=(x-a)(x-b)(a>b)的图象如图所示,则一次函数y=ax+b的图象正确的是( ).
A .
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
-1
1
1
1
1
-1
-1
-1
1
-1
D
7.在同一直角坐标系中二次函数y=ax2+bx+c
和反比例函数y= 的图象如图所示,则一次函数
y= x-b的图象可能是( ).
x
y
O
A .
B.
C.
D.
c
x
x
y
O
x
y
O
x
y
O
x
y
O
c
a
a<0
c>0
b>0
c
a
<0
-b<0
C
8.已知反比例函数y= (b≠0)的图象如图所示,则一次函数y= cx-a(c≠0)和二次函数y=ax2+bx+c
(a≠0)在同一直角坐标系中则的图象可能是( ).
x
y
O
A .
B.
C.
D.
b
x
x
y
O
x
y
O
x
y
O
x
y
O
a<0
b>0
c<0
D
c>0
a<0
b<0
c<0
b<0
c>0
a>0
b>0
-a<0
c<0
a>0
b>0
-a<0
c<0
-a>0
-a>0
9.抛物线y=ax2+bx+c(a≠0)的图象如图所示,
下列结论中 :
x
y
O
② a+b+c<0;
A . ① ②
B. ① ③ ④
C. ① ② ③ ④
D. ① ② ③ ④ ⑤
① abc>0;
③4a-2b+c>0;
④c-a>1;
-1
其中正确结论的序号是( ).
⑤a+b-c>1.
1
1
C
-2
10.如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),( ,y2)是抛物线上两点,则y1>y2.其中说法正确的是( ).
A.①② B.②③
C.①②④ D.②③④
5
2
C
11.如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(1,0),直线x=-0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:
①a-b=0;②当-2<x<1时,y>0;
③四边形ACBD是菱形;
④9a-3b+c>0
你认为其中正确的是( ).
A.②③④ B.①②④
C.①③④ D.①②③
x
y
A
B
M
O
C
D
D
12.抛物线y=ax2+bx+c(a≠0)的图象如图,它与x轴交于点(4,0),其对称轴为直线=1,下列结论中 :
x
y
O
②4a-2b+c>0;
A . 1个
B. 2个
C. 3个
D. 4个
①ac<0;
y随x的增大而增大;
④关于x的一元二次方程
x=1
正确的个数是( ).
ax2+bx+c=0有两个不相等的实数根.
4
③ 当x>2时,
C
13.抛物线y=ax2+bx+c(a≠0)的图象如图所示,
下列结论中 :
x
y
O
② b2>4ac;
⑥当x<-1时,y随x的增大而增大.
① abc<0;
③ 3a+c>0,
④ 4a+2b+c>0;⑤a+b≤m(am+b)(m为实数);
x=1
正确的有( ).
-1
A . 6个
B. 5个
C. 4个
D. 3个
D
14.抛物线y=ax2+bx+c(a≠0)如图所示,试
确定a、b、c、b2-4ac的符号
x
y
O
a 0, b 0,
c 0, b2-4ac 0.
>
<
>
>
15.抛物线y=ax2+bx+c(a≠0)如图所示,
试确定a、b、c、b2-4ac的符号.
x
y
O
a 0, b 0,
c 0, b2-4ac 0.
<
>
<
<
16.如图,二次函数y=ax2+bx+c(a>0)的对称轴是过点( 1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a-2b+c的值是 .
x
y
O
x=1
0
P
第21章 二次函数与反比例函数期末复习(3)
二次函数系数符号与图象的信息
沪科版
1.函数的图象
x
y
O
x
y
O
x
y
O
x
y
O
y=ax
(a>0)
y=ax+b
y=ax2+bx+c
y=
a
x
复习要点
2.函数的图象
x
y
O
x
y
O
x
y
O
x
y
O
y=ax
(a<0)
y=ax+b
y=ax2+bx+c
y=
a
x
复习要点
3.抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
确定抛物线的开口方向
开口向上
a>0
开口向下
a<0
x
y
O
x
y
O
a>0
a<0
复习要点
3.抛物线y=ax2+bx+c的符号问题:
(2)c的符号:
确定抛物线与y轴的交点位置:
交点在y轴正半轴
c>0
交点在y轴负半轴
c<0
交点在标原点
c=0
x
y
o
x
y
o
x
y
o
C
C
C
(3)b的符号:
由对称轴的位置确定:
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
简记为:左同右异
x
y
O
b
2a
-
x=
b
2a
-
x=
3.抛物线y=ax2+bx+c的符号问题:
(4) b2-4ac的符号:
确定抛物线与x轴交点个数
x
y
O
与x轴有2个交点
与x轴有1个交点
与x轴没有交点
b2-4ac>0
b2-4ac=0
b2-4ac<0
3.抛物线y=ax2+bx+c的符号问题:
2a-b
2a+b
a+b+c
a-b+c
4a+2b+c
4a-2b+c
b
2a
-
常与1比较
>1;
<1;
=1.
b
2a
-
常与1比较
>1;
<1;
=1.
x=1的函数值
>0,在x轴的上方
<0,在x轴的下方
x=-1的函数值
>0,在x轴的上方
<0,在x轴的下方
x=2的函数值
>0,在x轴的上方
<0,在x轴的下方
x=-2的函数值
>0,在x轴的上方
<0,在x轴的下方
复习要点
4.常见代数式的意义及其作用
抛物线y=ax2+bx+c(a≠0)如图所示,试
判断下来字母和代数式的符号.
a 0, b 0,
c 0, b2-4ac 0.
2a+b 0, 2a-b 0,
a+b+c 0, a-b+c 0.
4a+2b+c 0,4a-2b+c 0.
x
y
O
1
2
-1
<
>
>
>
=
<
>
<
>
<
例题解析
1.抛物线y=ax2+bx+c(a≠0)的图象如图所示,
则下列a、b、c间关系判断正确的是( ).
x
y
O
A . ab<0
C. a+b+c>0
B . bc<0
D.a-b+c<0;
练习巩固
D
2.已知一次函数y=ax-c的图象经过二、一、四象限,则二次函数y=ax2+c大致图象可能是( ).
A .
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
D
3.在同一直角坐标系中,二次函数y=ax2+bx
与一次函数y=ax+b的大致图象可能是( ).
A .
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
a>0
a>0
b>0
b=0
a>0
b>0
a>0
b>0
a>0
b<0
a<0
b<0
a>0
b>0
a>0
b<0
C
c=0
4.在同一直角坐标系中,二次函数y=ax2+bx +c与一次函数y=ax+c的大致图象可能是( ).
A .
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
a>0
c<0
a<0
c>0
a<0
a<0
c>0
c>0
a>0
c>0
c<0
a>0
a<0
c>0
a>0
c>0
B
5. 如图,二次函数y=ax2-a和反比例函数
y= 在同一直角坐标系中的图象可能是( ).
A .
B.
C.
D.
a
x
x
y
O
x
y
O
x
y
O
x
y
O
a<0
-a>0
a>0
a>0
-a<0
a>0
a<0
a<0
-a>0
a<0
a<0
-a<0
D
6.已知二次函数y=(x-a)(x-b)(a>b)的图象如图所示,则一次函数y=ax+b的图象正确的是( ).
A .
B.
C.
D.
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
-1
1
1
1
1
-1
-1
-1
1
-1
D
7.在同一直角坐标系中二次函数y=ax2+bx+c
和反比例函数y= 的图象如图所示,则一次函数
y= x-b的图象可能是( ).
x
y
O
A .
B.
C.
D.
c
x
x
y
O
x
y
O
x
y
O
x
y
O
c
a
a<0
c>0
b>0
c
a
<0
-b<0
C
8.已知反比例函数y= (b≠0)的图象如图所示,则一次函数y= cx-a(c≠0)和二次函数y=ax2+bx+c
(a≠0)在同一直角坐标系中则的图象可能是( ).
x
y
O
A .
B.
C.
D.
b
x
x
y
O
x
y
O
x
y
O
x
y
O
a<0
b>0
c<0
D
c>0
a<0
b<0
c<0
b<0
c>0
a>0
b>0
-a<0
c<0
a>0
b>0
-a<0
c<0
-a>0
-a>0
9.抛物线y=ax2+bx+c(a≠0)的图象如图所示,
下列结论中 :
x
y
O
② a+b+c<0;
A . ① ②
B. ① ③ ④
C. ① ② ③ ④
D. ① ② ③ ④ ⑤
① abc>0;
③4a-2b+c>0;
④c-a>1;
-1
其中正确结论的序号是( ).
⑤a+b-c>1.
1
1
C
-2
10.如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),( ,y2)是抛物线上两点,则y1>y2.其中说法正确的是( ).
A.①② B.②③
C.①②④ D.②③④
5
2
C
11.如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(1,0),直线x=-0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:
①a-b=0;②当-2<x<1时,y>0;
③四边形ACBD是菱形;
④9a-3b+c>0
你认为其中正确的是( ).
A.②③④ B.①②④
C.①③④ D.①②③
x
y
A
B
M
O
C
D
D
12.抛物线y=ax2+bx+c(a≠0)的图象如图,它与x轴交于点(4,0),其对称轴为直线=1,下列结论中 :
x
y
O
②4a-2b+c>0;
A . 1个
B. 2个
C. 3个
D. 4个
①ac<0;
y随x的增大而增大;
④关于x的一元二次方程
x=1
正确的个数是( ).
ax2+bx+c=0有两个不相等的实数根.
4
③ 当x>2时,
C
13.抛物线y=ax2+bx+c(a≠0)的图象如图所示,
下列结论中 :
x
y
O
② b2>4ac;
⑥当x<-1时,y随x的增大而增大.
① abc<0;
③ 3a+c>0,
④ 4a+2b+c>0;⑤a+b≤m(am+b)(m为实数);
x=1
正确的有( ).
-1
A . 6个
B. 5个
C. 4个
D. 3个
D
14.抛物线y=ax2+bx+c(a≠0)如图所示,试
确定a、b、c、b2-4ac的符号
x
y
O
a 0, b 0,
c 0, b2-4ac 0.
>
<
>
>
15.抛物线y=ax2+bx+c(a≠0)如图所示,
试确定a、b、c、b2-4ac的符号.
x
y
O
a 0, b 0,
c 0, b2-4ac 0.
<
>
<
<
16.如图,二次函数y=ax2+bx+c(a>0)的对称轴是过点( 1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a-2b+c的值是 .
x
y
O
x=1
0
P
