第21章二次函数与反比例函数期末复习(4)二次函数的应用 课件(共26张PPT)
文档属性
| 名称 | 第21章二次函数与反比例函数期末复习(4)二次函数的应用 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 906.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 16:00:09 | ||
图片预览


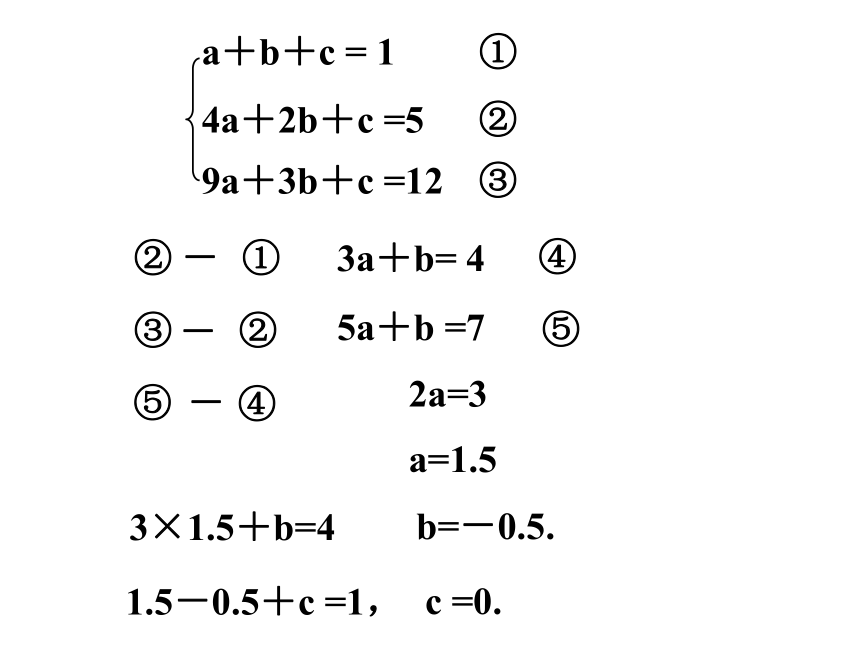
文档简介
(共26张PPT)
第21章 二次函数与反比例函数期末复习(4)
二次函数的应用
沪科版
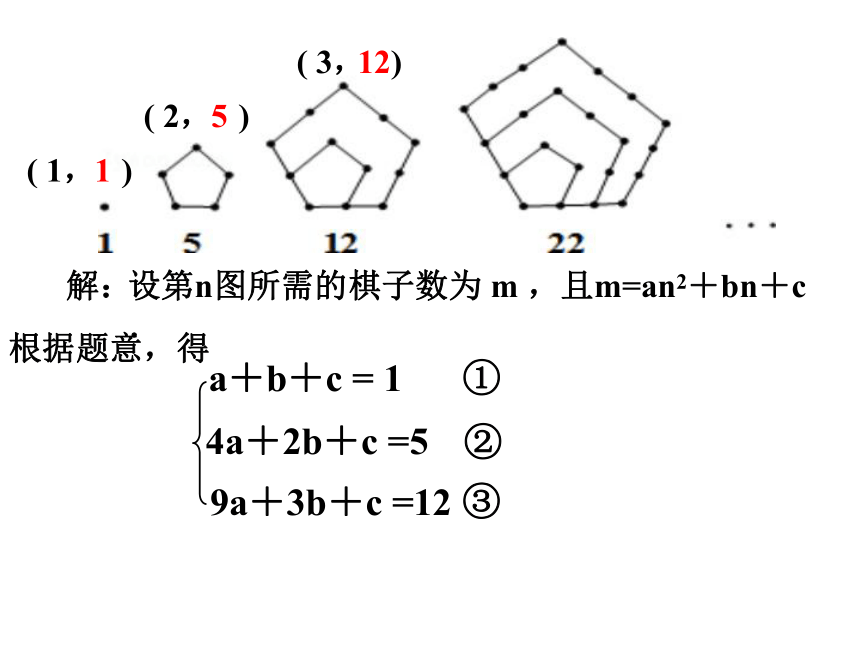
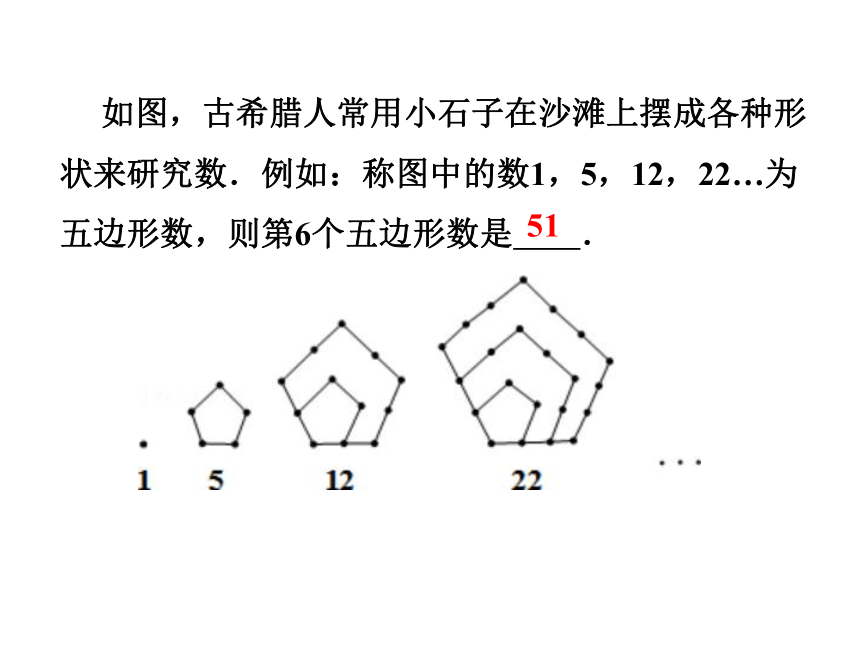
例.如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第6个五边形数是 .
( 1, )
1
( 2, )
5
( 3, )
12
二次函数的应用
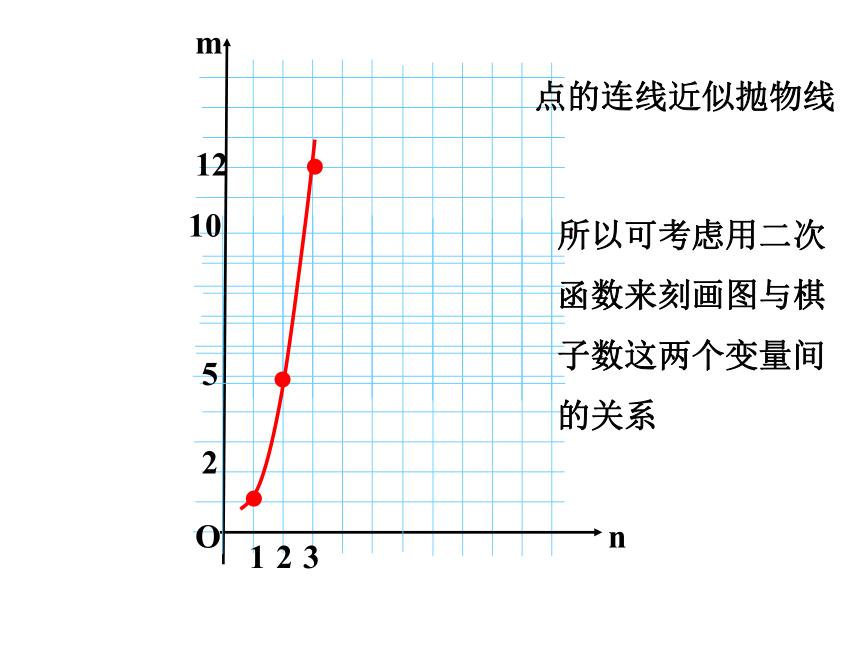
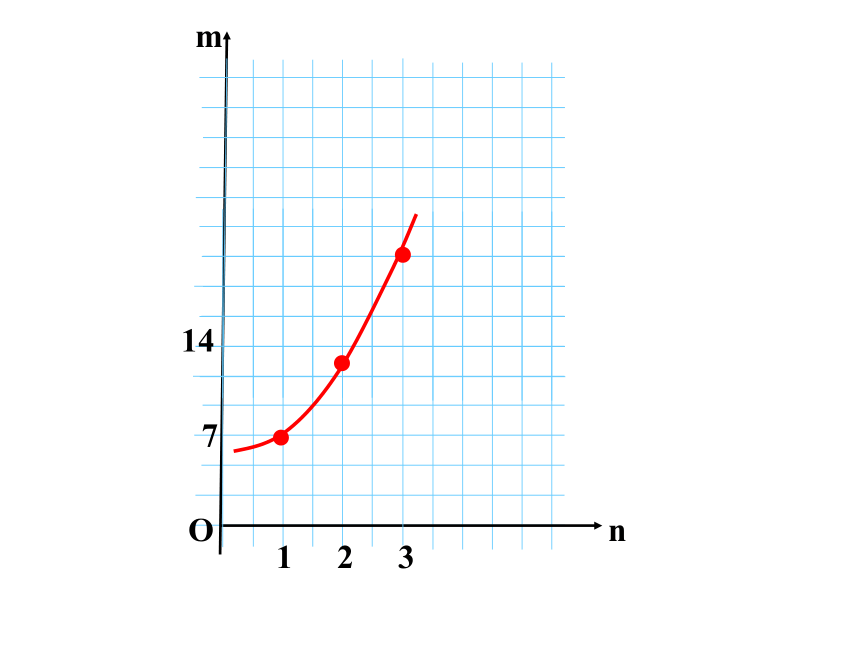
将上述三组有序数对描点到平面直角坐标系
n
m
1
2
O
3
2
5
10
12
点的连线近似抛物线
所以可考虑用二次函数来刻画图与棋子数这两个变量间的关系
设第n图所需的棋子数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =5
9a+3b+c =12
①
②
③
a+b+c = 1
( 1, )
1
( 2, )
5
( 3, )
12
4a+2b+c =5
a+b+c = 1
9a+3b+c =12
①
②
③
②
-
3a+b= 4
-
③
5a+b =7
2a=3
a=1.5
b=-0.5.
1.5-0.5+c =1,
c =0.
④
⑤
⑤
-
①
④
②
3×1.5+b=4
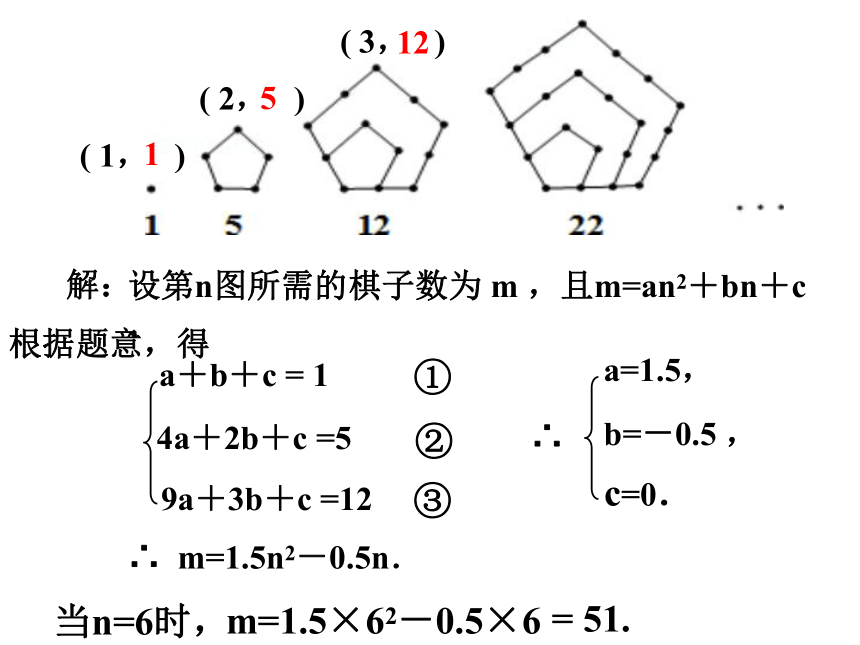
设第n图所需的棋子数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =5
9a+3b+c =12
①
②
③
a+b+c = 1
∴
c=0.
∴ m=1.5n2-0.5n.
a=1.5,
b=-0.5 ,
当n=6时,
m=1.5×62-0.5×6
= 51.
( 1, )
1
( 2, )
5
( 3, )
12
如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第6个五边形数是 .
51
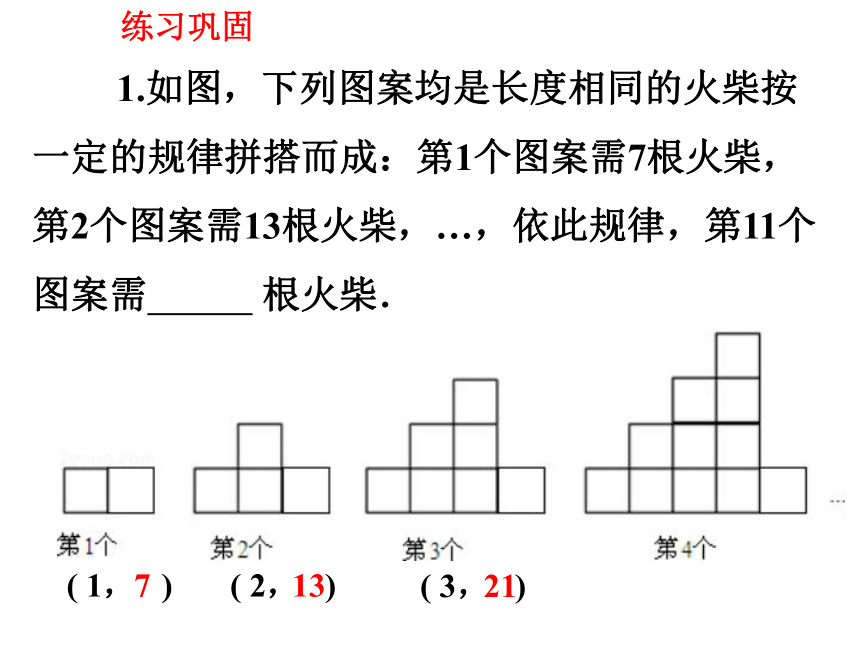
1.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需 根火柴.
( 1, )
7
( 2, )
13
( 3, )
21
练习巩固
n
m
1
2
O
3
7
14
( 1, )
7
( 2, )
13
( 3, )
21
设第n图所需的火柴数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =13
9a+3b+c =21
①
②
③
a+b+c = 7
4a+2b+c =13
a+b+c = 7
9a+3b+c =21
①
②
③
②
-
3a+b= 6
-
③
5a+b=8
2a=2
a=1
3+b = 6,
b=3.
c =3
④
⑤
⑤
-
①
④
②
1+3+c = 7
( 1, )
7
( 2, )
13
( 3, )
21
设第n图所需的火柴数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =13
9a+3b+c =21
①
②
③
a+b+c = 7
∴
c=3.
∴m=n2+3n+3.
( 4, )
31
a=1,
b=3 ,
当n=11时,
m=1×112+3×11+3
= 157.
1.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需 根火柴.
( 1, )
7
( 2, )
13
( 3, )
21
练习巩固
157
2.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为 .
2.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为 .
( 1, )
1
( 2, )
6
( 3, )
16
设第n图所需的棋子数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =6
9a+3b+c =16
①
②
③
a+b+c = 1
( 1, )
1
( 2, )
6
( 3, )
16
4a+2b+c =6
a+b+c = 1
9a+3b+c =16
①
②
③
②
-
3a+b= 5
-
③
5a+b =10
2a=5
a=2.5
b=-2.5.
2.5-2.5+c =1,
c =1.
④
⑤
⑤
-
①
④
②
3×2.5+b=5
设第n图所需的棋子数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =6
9a+3b+c =16
①
②
③
a+b+c = 1
∴
c=1.
∴ m=2.5n2-2.5n+1
a=2.5,
b=-2.5 ,
当n=6时,
m=2.5×62-2.5×6+1
= 76.
( 1, )
1
( 2, )
6
( 3, )
16
2.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为 .
( 1, )
1
( 2, )
6
( 3, )
16
76
3.如图是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n根火柴棍时,设摆出的正方形所用的火柴棍的根数为s,则
s= .(用n的代数式表示s)
图(4)
……
n=1
n=2
n=3
( 1, )
4
( 2, )
12
( 3, )
24
3.(2009广西梧州3分)图(4)是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n根火柴棍时,设摆出的正方形所用的火柴棍的根数为s,则s= .(用n的代数式表示s)
图(4)
……
n=1
n=2
n=3
( 1, )
4
( 2, )
12
( 3, )
24
( 1, )
4
( 2, )
13
( 3, )
21
设第n图所需的火柴数为 s ,且s=an2+bn+c.
解:
根据题意,得
4a+2b+c =12
9a+3b+c =24
①
②
③
a+b+c = 4
图(3)
……
n=1
n=2
n=3
4a+2b+c =12
a+b+c = 4
9a+3b+c =24
①
②
③
②
-
3a+b= 8
-
③
5a+b =12
2a=4
a=2
b=2.
c =0.
④
⑤
⑤
-
①
④
②
3×2+b=8
2+2+c = 4
设第n图所需的火柴数为 s ,且s=an2+bn+c.
解:
根据题意,得
4a+2b+c =12
9a+3b+c =24
①
②
③
a+b+c = 4
∴
c=0.
∴s=2n2+2n.
a=2,
b=2 ,
( 1, )
4
( 2, )
12
( 3, )
24
图(3)
……
n=1
n=2
n=3
3.如图是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n根火柴棍时,设摆出的正方形所用的火柴棍的根数为s,
则s= .(用n的代数式表示s)
……
n=1
n=2
n=3
2n2+2n
( 1, )
4
( 2, )
12
( 3, )
24
4.观察下列图形中点的个数,若按其规律再画下去,可以得到第n个图形中所有的个数为 (用含n的代数式表示).
( 1, )
4
( 2, )
9
( 3, )
16
(n+1)2
第21章 二次函数与反比例函数期末复习(4)
二次函数的应用
沪科版
例.如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第6个五边形数是 .
( 1, )
1
( 2, )
5
( 3, )
12
二次函数的应用
将上述三组有序数对描点到平面直角坐标系
n
m
1
2
O
3
2
5
10
12
点的连线近似抛物线
所以可考虑用二次函数来刻画图与棋子数这两个变量间的关系
设第n图所需的棋子数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =5
9a+3b+c =12
①
②
③
a+b+c = 1
( 1, )
1
( 2, )
5
( 3, )
12
4a+2b+c =5
a+b+c = 1
9a+3b+c =12
①
②
③
②
-
3a+b= 4
-
③
5a+b =7
2a=3
a=1.5
b=-0.5.
1.5-0.5+c =1,
c =0.
④
⑤
⑤
-
①
④
②
3×1.5+b=4
设第n图所需的棋子数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =5
9a+3b+c =12
①
②
③
a+b+c = 1
∴
c=0.
∴ m=1.5n2-0.5n.
a=1.5,
b=-0.5 ,
当n=6时,
m=1.5×62-0.5×6
= 51.
( 1, )
1
( 2, )
5
( 3, )
12
如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第6个五边形数是 .
51
1.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需 根火柴.
( 1, )
7
( 2, )
13
( 3, )
21
练习巩固
n
m
1
2
O
3
7
14
( 1, )
7
( 2, )
13
( 3, )
21
设第n图所需的火柴数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =13
9a+3b+c =21
①
②
③
a+b+c = 7
4a+2b+c =13
a+b+c = 7
9a+3b+c =21
①
②
③
②
-
3a+b= 6
-
③
5a+b=8
2a=2
a=1
3+b = 6,
b=3.
c =3
④
⑤
⑤
-
①
④
②
1+3+c = 7
( 1, )
7
( 2, )
13
( 3, )
21
设第n图所需的火柴数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =13
9a+3b+c =21
①
②
③
a+b+c = 7
∴
c=3.
∴m=n2+3n+3.
( 4, )
31
a=1,
b=3 ,
当n=11时,
m=1×112+3×11+3
= 157.
1.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需 根火柴.
( 1, )
7
( 2, )
13
( 3, )
21
练习巩固
157
2.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为 .
2.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为 .
( 1, )
1
( 2, )
6
( 3, )
16
设第n图所需的棋子数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =6
9a+3b+c =16
①
②
③
a+b+c = 1
( 1, )
1
( 2, )
6
( 3, )
16
4a+2b+c =6
a+b+c = 1
9a+3b+c =16
①
②
③
②
-
3a+b= 5
-
③
5a+b =10
2a=5
a=2.5
b=-2.5.
2.5-2.5+c =1,
c =1.
④
⑤
⑤
-
①
④
②
3×2.5+b=5
设第n图所需的棋子数为 m ,且m=an2+bn+c.
解:
根据题意,得
4a+2b+c =6
9a+3b+c =16
①
②
③
a+b+c = 1
∴
c=1.
∴ m=2.5n2-2.5n+1
a=2.5,
b=-2.5 ,
当n=6时,
m=2.5×62-2.5×6+1
= 76.
( 1, )
1
( 2, )
6
( 3, )
16
2.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为 .
( 1, )
1
( 2, )
6
( 3, )
16
76
3.如图是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n根火柴棍时,设摆出的正方形所用的火柴棍的根数为s,则
s= .(用n的代数式表示s)
图(4)
……
n=1
n=2
n=3
( 1, )
4
( 2, )
12
( 3, )
24
3.(2009广西梧州3分)图(4)是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n根火柴棍时,设摆出的正方形所用的火柴棍的根数为s,则s= .(用n的代数式表示s)
图(4)
……
n=1
n=2
n=3
( 1, )
4
( 2, )
12
( 3, )
24
( 1, )
4
( 2, )
13
( 3, )
21
设第n图所需的火柴数为 s ,且s=an2+bn+c.
解:
根据题意,得
4a+2b+c =12
9a+3b+c =24
①
②
③
a+b+c = 4
图(3)
……
n=1
n=2
n=3
4a+2b+c =12
a+b+c = 4
9a+3b+c =24
①
②
③
②
-
3a+b= 8
-
③
5a+b =12
2a=4
a=2
b=2.
c =0.
④
⑤
⑤
-
①
④
②
3×2+b=8
2+2+c = 4
设第n图所需的火柴数为 s ,且s=an2+bn+c.
解:
根据题意,得
4a+2b+c =12
9a+3b+c =24
①
②
③
a+b+c = 4
∴
c=0.
∴s=2n2+2n.
a=2,
b=2 ,
( 1, )
4
( 2, )
12
( 3, )
24
图(3)
……
n=1
n=2
n=3
3.如图是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n根火柴棍时,设摆出的正方形所用的火柴棍的根数为s,
则s= .(用n的代数式表示s)
……
n=1
n=2
n=3
2n2+2n
( 1, )
4
( 2, )
12
( 3, )
24
4.观察下列图形中点的个数,若按其规律再画下去,可以得到第n个图形中所有的个数为 (用含n的代数式表示).
( 1, )
4
( 2, )
9
( 3, )
16
(n+1)2
