湖北省武汉市武汉榕霖文化艺术学院2023-2024学年高一上学期12月月考数学试卷(含解析)
文档属性
| 名称 | 湖北省武汉市武汉榕霖文化艺术学院2023-2024学年高一上学期12月月考数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 874.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 12:15:25 | ||
图片预览




文档简介
武汉榕霖文化艺术学院2023-2024学年上学期高一年级12月考试
数学试卷
(满分:150分 时间:120分钟)
一 单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,则集合( )
A. B. C. D.
2.已知集合,若,则( )
A.1 B. C.2 D.-1
3.已知函数,则的值是( )
A. B. C. D.2
4.设,则( )
A. B.
C. D.
5.已知函数,则对任意实数,有( )
A. B.
C. D.
6.式子的计算结果为( )
A.1 B. C. D.
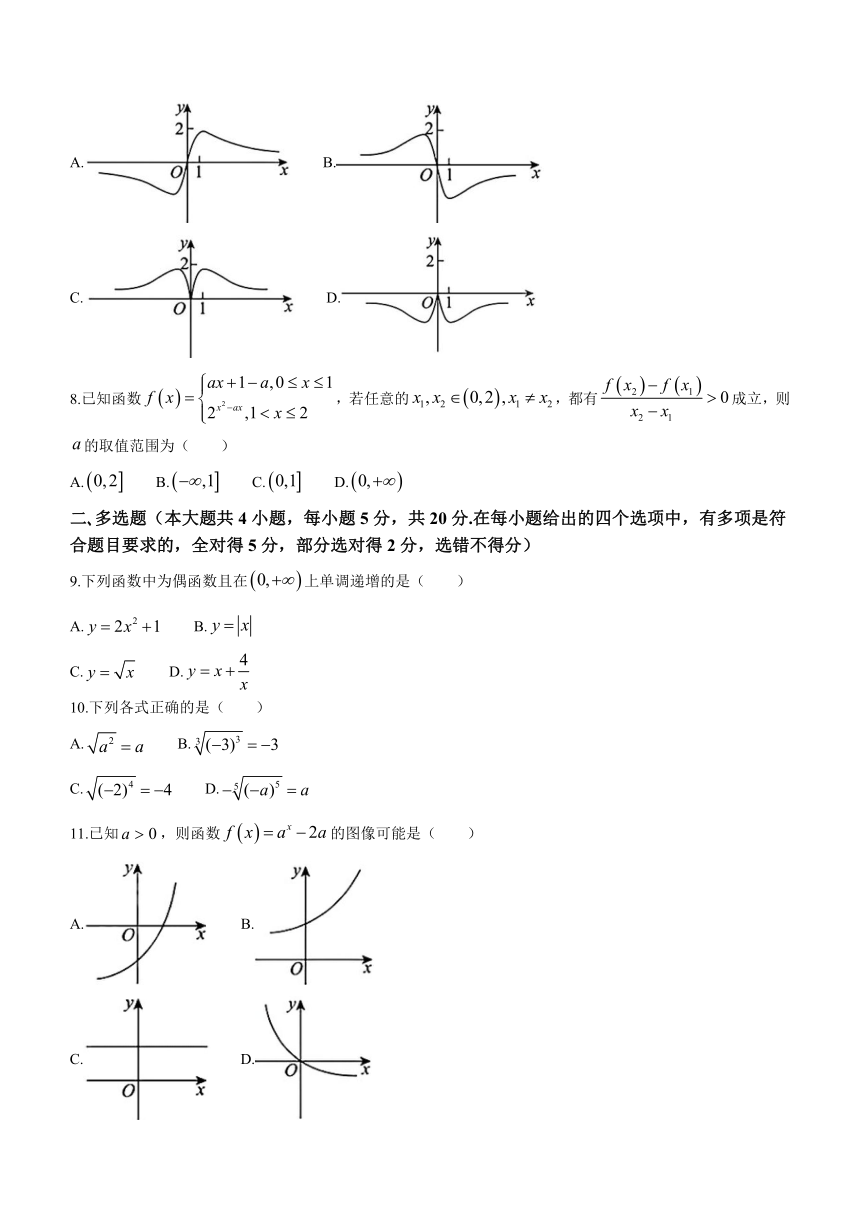
7.函数的图象大致为( )
A. B.
C. D.
8.已知函数,若任意的,都有成立,则的取值范围为( )
A. B. C. D.
二 多选题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的,全对得5分,部分选对得2分,选错不得分)
9.下列函数中为偶函数且在上单调递增的是( )
A. B.
C. D.
10.下列各式正确的是( )
A. B.
C. D.
11.已知,则函数的图像可能是( )
A. B.
C. D.
12.设是定义在上的奇函数,且在上单调递减,,则( )
A.在上单调递减
B.
C.不等式的解集为
D.的图象与轴只有1个交点
三 填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.函数的定义域是__________.
14.若且,则函数的图像恒过的定点的坐标为__________.
15.从甲市到乙市的电话费由函数给出,其中为不超过的最大整数,则从甲市到乙市的电话费为__________元.
16.若函数是上的偶函数,且当时,,则__________.
四 解答题(本大题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤)
17.求值:
(1)
(2)
18.已知函数.
(1)若,求实数的值;
(2)若,恒成立,求:实数的取值范围.
19.已知幂函数为偶函数.
(1)求的解析式;
(2)若函数在区间上的最大值为9,求实数的值.
20.已知为二次函数,且满足:对称轴为.
(1)求函数的解析式,并求图像的顶点坐标;
(2)在给出的平面直角坐标系中画出的图象,并直接写出函数的单调增区间.
21.已知函数
(1)判断并证明函数的奇偶性;
(2)判断函数在区间上的单调性(不必写出过程),并解不等式
22.已知函数是奇函数.
(1)求实数的值;
(2)设关于的不等式的解集为.若集合中的整数元素只有两个,求实数的取值范围.
12月数学月考参考答案
1.D
【来源】福建省福州市屏东中学2023-2024学年高一上学期10月月考数学试题
【分析】根据并集的知识求得正确答案.
【详解】依题意,.
故选:D
2.B
【来源】广西普通高中2024届高三跨市联合适应性训练检测卷数学试题
【分析】先由题意得或,从而分类讨论各元素的值并检验即可得解.
【详解】因为,
所以或,
若,则,此时,不满足集合的互异性;
若,则,此时,符合题意;
若,则,此时,不满足集合的互异性.
综上,.
故选:B
3.C
【来源】天津市滨海新区塘沽第一中学2023-2024学年高一上学期11月期中数
学试题
【分析】直接代入分段函数计算即可.
【详解】由已知,
.
故选:C.
4.A
【来源】北京市大兴区2023-2024学年高一上学期期中检测数学试题
【分析】利用指数函数和幂函数的单调性比较大小.
【详解】因为为减函数,所以,即;
因为在为增函数,所以,即;
所以.
故选:A.
5.B
【来源】2022.年北京市高考数学试题
【分析】直接代入计算,注意通分不要计算错误.
【详解】,故A错误,B正确;,不是常数,故
CD错误;
故选:B.
6.D
【来源】浙江省台州市玉环中学2021-2022学年高一上学期第一次月考数学试题
【分析】由指数运算法则直接计算可得结果.
【详解】.
故选:D.
7.A
【来源】2020年天津市高考数学试卷
【分析】由题意首先确定函数的奇偶性,然后考查函数在特殊点的函数值排除错误选项即可确定函数的图象.
【详解】由函数的解析式可得:,则函数为奇函数,
其图象关于坐标原点对称,选项CD错误;
当时,,选项B错误.
故选:A.
【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的
左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除 饰选选项.
8.C
【来源】贵州省黔东南州九校2023-2024学年高三上学期11月月考数学试题
【分析】首先分析出函数单调递增,再根据函数单调性定义得到不等式组,解出即可.
【详解】因为对于,都有成立,所以函数是增函数,
则函数和均为增函数,且有,
即,解得.
故选:C.
9.AB
【来源】四川省南充市闽中市阆中中学校2023-2024学年高一上学期11月月考数学试题
【分析】根据函数奇偶性定义,并利用函数单调性逐一判断即可得出结论.
【详解】对于,满足偶函数定义,利用二次函数性质可得其在
上单调递增,故A正确;
对于,易知,即满足偶函数定义,且当时,为单调递增,即B正确;
对于C,显然的定义域为,不关于原点对称,因此C错误;
对于,易知的定义域为,且满足,即是奇函数,故错误;
故选:AB
10.BD
【来源】第三章指数运算与指数函数能力提升单元达标测试卷-2022-2023学年高一上学期数学北师大版(2019)必修第一册
【分析】利用根式的运算直接求解.
【详解】当为偶数时,故A,C选项中的式子不正确;
当为奇数时,,
则,
故B,D选项中的式子正确.
故选:BD.
11.AD
【来源】河北省衡水市第十三中学2024届高三上学期开学考试数学试题
【分析】通过特值法,排除错误选项,通过的取值,判断函数的图象的形状,推出结果即可.
【详解】由于当时,,排除,
当时,,此时函数图象对应的图形可能为A,
当时,,此时函数图象对应的的图形可能为.
故选:AD.
12.ABC
【来源】甘肃省临夏州积石山保安族东乡族撒拉族自治县积石中学2022-2023学年高一上学期期中检测数学试题
【分析】根据函数奇偶性,单调性,图象解决即可.
【详解】可作满足题意的下图(不唯一),仅参考
对A:因为是定义在上的奇函数,且在上单调递减,由奇函数的性质有在上单调递减,故选项A正确;
对B:因为是定义在上的奇函数,且在上单调递减,
,所以,所以,故选项B正确;
对C:由选项A与题意可得的解集为,故选项C正确.
对D:由题意,,又是定义在上的奇函数,所以,
所以的图象与轴有3个交点,故选项错误;故选:ABC.
13.
【来源】人教A版(2019)必修第一册数学奇书第四章指数函数与对数函数4.2指数函数第1课时指数函数的概念 图象和性质
【分析】根据二次根式的性质以及指数函数的单调性可解出原函数的定义域.
【详解】对于函数,由可得,解得.
因此,函数的定义域为.
故答案为:.
14.
【来源】2023版湘教版(2019)必修第一册突围者第4章第二节指数函数
【分析】任意指数函数一定过定点,根据该性质求解.
【详解】令,得,所以,所以函数的
图像恒过定点.
故答案为:
15.5.3
【来源】贵州省六盘水市纽绅中学2023-2024学年高一上学期10月月考数学试题
【分析】代入求值即可.
【详解】依题意知.
故答案为:5.3
16.-2
【来源】四川省内江市第六中学2023-2024学年高一上学期期中考试数学试卷
【分析】根据题意,由偶函数的性质,代入计算,即可得到结果.
【详解】因为函数是上的偶函数,则,
由当时,,则,
所以.
故答案为:-2
17.
【详解】(1)
(2)原式
18.(1)
(1)
【来源】天津市红桥区2018-2019学年高二下学期学业水平模拟考试数学试题
【分析】(1)直接将代入解析式,解方程即可得到答案;
(2)对进行分类讨论,若恒成立;若则可得抛物线开口向下,且与无交点;
【详解】(1)因为,
所以;
(2)当时,恒成立,
当,
综上所述:时,恒成立.
19.(1)的解析式为;(2)实数的值为2.
【来源】河南省焦作市普通高中2021-2022学年高一上学期期中考试数学试题
【详解】解:(1)由题,解得或-2,
又因为为偶函数,
则为偶数,从而;
故求的解析式为
(2)由(1)得:
函数的对称轴为:,开口朝上
由题意得在区间上,解得
所以实数的值为2.
20.(1),顶点坐标为.
(2)图象见解析,函数的增区间为:.(开区间和闭区间均可)
【来源】西藏拉萨市第二高级中学2022-2023学年高一上学期期末考试数学试题
【分析】(1)根据已知条件列出方程组即可求解;(2)作出函数图象可求解.
【详解】(1)设函数为,
所以解得所以,
所以,所以顶点坐标为.
(2)图象如图所示,
函数的增区间为:
21.(1)函数是R上的偶函数,证明见解析
(2)函数在上单调递增,
【来源】安徽省合肥市第六中学 第八中学 168中学等校2021-2022学年高一上学期期末联考数学试题
【分析】(1)利用偶函数的定义判断并证明函数为偶函数;
(2)根据指数函数和复合函数及函数的加减合成的单调性规律判定函数的单调性,然后结合函数是偶函数,将不等式转化为,进而两边同时平方,等价转化为二次方程,求解即得.
【详解】(1)证明:依题意,函数的定义域为R.对于任意,
都有,
所以函数是R上的偶函数.
(2)解:函数在上单调递增.
因为函数R上的偶数函数,所以
等价于.因为函数在上单调递增,
所以,即,解得,
所以不等式的解集为.
22.(1)
(2)
【来源】福建省福州市闵江口协作体2024届高三上学期11月期中联考数学试题
【分析】(1)由题意可得,检验,即可求解;
(2)利用函数的奇偶性和单调性解不等式,可得,分类讨论当 时对应的解集,结合题意即可求解.
【详解】(1)由题意知,是定义域为R上的奇函数,
则,即,解得,
经检验,符合题意,所以;
(2)由(1)知,,则,
又函数在R上单调递增,所以函数在R上单调递增,
由,
得,即.
当时,,解得,此时集合A不满足题意;
当时,,
对于方程,
若,则,不等式的解集为,此时集合A不满足题意;
若,则,不等式的解集为,
又集合A有2个整数元素,所以,则,解得;
若,则,不等式的解集为,此时集合A不满足题意;
若,则,不等式的解集为,
又集合A有2个整数元素,所以,则,无解.
综上,实数a的取值范围为.
数学试卷
(满分:150分 时间:120分钟)
一 单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,则集合( )
A. B. C. D.
2.已知集合,若,则( )
A.1 B. C.2 D.-1
3.已知函数,则的值是( )
A. B. C. D.2
4.设,则( )
A. B.
C. D.
5.已知函数,则对任意实数,有( )
A. B.
C. D.
6.式子的计算结果为( )
A.1 B. C. D.
7.函数的图象大致为( )
A. B.
C. D.
8.已知函数,若任意的,都有成立,则的取值范围为( )
A. B. C. D.
二 多选题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的,全对得5分,部分选对得2分,选错不得分)
9.下列函数中为偶函数且在上单调递增的是( )
A. B.
C. D.
10.下列各式正确的是( )
A. B.
C. D.
11.已知,则函数的图像可能是( )
A. B.
C. D.
12.设是定义在上的奇函数,且在上单调递减,,则( )
A.在上单调递减
B.
C.不等式的解集为
D.的图象与轴只有1个交点
三 填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.函数的定义域是__________.
14.若且,则函数的图像恒过的定点的坐标为__________.
15.从甲市到乙市的电话费由函数给出,其中为不超过的最大整数,则从甲市到乙市的电话费为__________元.
16.若函数是上的偶函数,且当时,,则__________.
四 解答题(本大题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤)
17.求值:
(1)
(2)
18.已知函数.
(1)若,求实数的值;
(2)若,恒成立,求:实数的取值范围.
19.已知幂函数为偶函数.
(1)求的解析式;
(2)若函数在区间上的最大值为9,求实数的值.
20.已知为二次函数,且满足:对称轴为.
(1)求函数的解析式,并求图像的顶点坐标;
(2)在给出的平面直角坐标系中画出的图象,并直接写出函数的单调增区间.
21.已知函数
(1)判断并证明函数的奇偶性;
(2)判断函数在区间上的单调性(不必写出过程),并解不等式
22.已知函数是奇函数.
(1)求实数的值;
(2)设关于的不等式的解集为.若集合中的整数元素只有两个,求实数的取值范围.
12月数学月考参考答案
1.D
【来源】福建省福州市屏东中学2023-2024学年高一上学期10月月考数学试题
【分析】根据并集的知识求得正确答案.
【详解】依题意,.
故选:D
2.B
【来源】广西普通高中2024届高三跨市联合适应性训练检测卷数学试题
【分析】先由题意得或,从而分类讨论各元素的值并检验即可得解.
【详解】因为,
所以或,
若,则,此时,不满足集合的互异性;
若,则,此时,符合题意;
若,则,此时,不满足集合的互异性.
综上,.
故选:B
3.C
【来源】天津市滨海新区塘沽第一中学2023-2024学年高一上学期11月期中数
学试题
【分析】直接代入分段函数计算即可.
【详解】由已知,
.
故选:C.
4.A
【来源】北京市大兴区2023-2024学年高一上学期期中检测数学试题
【分析】利用指数函数和幂函数的单调性比较大小.
【详解】因为为减函数,所以,即;
因为在为增函数,所以,即;
所以.
故选:A.
5.B
【来源】2022.年北京市高考数学试题
【分析】直接代入计算,注意通分不要计算错误.
【详解】,故A错误,B正确;,不是常数,故
CD错误;
故选:B.
6.D
【来源】浙江省台州市玉环中学2021-2022学年高一上学期第一次月考数学试题
【分析】由指数运算法则直接计算可得结果.
【详解】.
故选:D.
7.A
【来源】2020年天津市高考数学试卷
【分析】由题意首先确定函数的奇偶性,然后考查函数在特殊点的函数值排除错误选项即可确定函数的图象.
【详解】由函数的解析式可得:,则函数为奇函数,
其图象关于坐标原点对称,选项CD错误;
当时,,选项B错误.
故选:A.
【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的
左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除 饰选选项.
8.C
【来源】贵州省黔东南州九校2023-2024学年高三上学期11月月考数学试题
【分析】首先分析出函数单调递增,再根据函数单调性定义得到不等式组,解出即可.
【详解】因为对于,都有成立,所以函数是增函数,
则函数和均为增函数,且有,
即,解得.
故选:C.
9.AB
【来源】四川省南充市闽中市阆中中学校2023-2024学年高一上学期11月月考数学试题
【分析】根据函数奇偶性定义,并利用函数单调性逐一判断即可得出结论.
【详解】对于,满足偶函数定义,利用二次函数性质可得其在
上单调递增,故A正确;
对于,易知,即满足偶函数定义,且当时,为单调递增,即B正确;
对于C,显然的定义域为,不关于原点对称,因此C错误;
对于,易知的定义域为,且满足,即是奇函数,故错误;
故选:AB
10.BD
【来源】第三章指数运算与指数函数能力提升单元达标测试卷-2022-2023学年高一上学期数学北师大版(2019)必修第一册
【分析】利用根式的运算直接求解.
【详解】当为偶数时,故A,C选项中的式子不正确;
当为奇数时,,
则,
故B,D选项中的式子正确.
故选:BD.
11.AD
【来源】河北省衡水市第十三中学2024届高三上学期开学考试数学试题
【分析】通过特值法,排除错误选项,通过的取值,判断函数的图象的形状,推出结果即可.
【详解】由于当时,,排除,
当时,,此时函数图象对应的图形可能为A,
当时,,此时函数图象对应的的图形可能为.
故选:AD.
12.ABC
【来源】甘肃省临夏州积石山保安族东乡族撒拉族自治县积石中学2022-2023学年高一上学期期中检测数学试题
【分析】根据函数奇偶性,单调性,图象解决即可.
【详解】可作满足题意的下图(不唯一),仅参考
对A:因为是定义在上的奇函数,且在上单调递减,由奇函数的性质有在上单调递减,故选项A正确;
对B:因为是定义在上的奇函数,且在上单调递减,
,所以,所以,故选项B正确;
对C:由选项A与题意可得的解集为,故选项C正确.
对D:由题意,,又是定义在上的奇函数,所以,
所以的图象与轴有3个交点,故选项错误;故选:ABC.
13.
【来源】人教A版(2019)必修第一册数学奇书第四章指数函数与对数函数4.2指数函数第1课时指数函数的概念 图象和性质
【分析】根据二次根式的性质以及指数函数的单调性可解出原函数的定义域.
【详解】对于函数,由可得,解得.
因此,函数的定义域为.
故答案为:.
14.
【来源】2023版湘教版(2019)必修第一册突围者第4章第二节指数函数
【分析】任意指数函数一定过定点,根据该性质求解.
【详解】令,得,所以,所以函数的
图像恒过定点.
故答案为:
15.5.3
【来源】贵州省六盘水市纽绅中学2023-2024学年高一上学期10月月考数学试题
【分析】代入求值即可.
【详解】依题意知.
故答案为:5.3
16.-2
【来源】四川省内江市第六中学2023-2024学年高一上学期期中考试数学试卷
【分析】根据题意,由偶函数的性质,代入计算,即可得到结果.
【详解】因为函数是上的偶函数,则,
由当时,,则,
所以.
故答案为:-2
17.
【详解】(1)
(2)原式
18.(1)
(1)
【来源】天津市红桥区2018-2019学年高二下学期学业水平模拟考试数学试题
【分析】(1)直接将代入解析式,解方程即可得到答案;
(2)对进行分类讨论,若恒成立;若则可得抛物线开口向下,且与无交点;
【详解】(1)因为,
所以;
(2)当时,恒成立,
当,
综上所述:时,恒成立.
19.(1)的解析式为;(2)实数的值为2.
【来源】河南省焦作市普通高中2021-2022学年高一上学期期中考试数学试题
【详解】解:(1)由题,解得或-2,
又因为为偶函数,
则为偶数,从而;
故求的解析式为
(2)由(1)得:
函数的对称轴为:,开口朝上
由题意得在区间上,解得
所以实数的值为2.
20.(1),顶点坐标为.
(2)图象见解析,函数的增区间为:.(开区间和闭区间均可)
【来源】西藏拉萨市第二高级中学2022-2023学年高一上学期期末考试数学试题
【分析】(1)根据已知条件列出方程组即可求解;(2)作出函数图象可求解.
【详解】(1)设函数为,
所以解得所以,
所以,所以顶点坐标为.
(2)图象如图所示,
函数的增区间为:
21.(1)函数是R上的偶函数,证明见解析
(2)函数在上单调递增,
【来源】安徽省合肥市第六中学 第八中学 168中学等校2021-2022学年高一上学期期末联考数学试题
【分析】(1)利用偶函数的定义判断并证明函数为偶函数;
(2)根据指数函数和复合函数及函数的加减合成的单调性规律判定函数的单调性,然后结合函数是偶函数,将不等式转化为,进而两边同时平方,等价转化为二次方程,求解即得.
【详解】(1)证明:依题意,函数的定义域为R.对于任意,
都有,
所以函数是R上的偶函数.
(2)解:函数在上单调递增.
因为函数R上的偶数函数,所以
等价于.因为函数在上单调递增,
所以,即,解得,
所以不等式的解集为.
22.(1)
(2)
【来源】福建省福州市闵江口协作体2024届高三上学期11月期中联考数学试题
【分析】(1)由题意可得,检验,即可求解;
(2)利用函数的奇偶性和单调性解不等式,可得,分类讨论当 时对应的解集,结合题意即可求解.
【详解】(1)由题意知,是定义域为R上的奇函数,
则,即,解得,
经检验,符合题意,所以;
(2)由(1)知,,则,
又函数在R上单调递增,所以函数在R上单调递增,
由,
得,即.
当时,,解得,此时集合A不满足题意;
当时,,
对于方程,
若,则,不等式的解集为,此时集合A不满足题意;
若,则,不等式的解集为,
又集合A有2个整数元素,所以,则,解得;
若,则,不等式的解集为,此时集合A不满足题意;
若,则,不等式的解集为,
又集合A有2个整数元素,所以,则,无解.
综上,实数a的取值范围为.
同课章节目录
