第二十九章 反比例函数单元测试卷(含解析)
文档属性
| 名称 | 第二十九章 反比例函数单元测试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 05:37:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2023-2024学年 人教版(五四制)九年级上册 第二十九章 反比例函数 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.反比例函数的图象上有两点、,且,则m的取值范围是( ).
A. B. C. D.
2.下列函数的图像在每一个象限内,随着的增大而增大的是( )
A. B. C. D.
3.如图,在平面直角坐标系中,函数与反比例函数交于A、B两点,点C在x轴上,且,若,则k的值是( )
A. B.6 C. D.
4.如图所示,如果函数与的图象交于A,B两点,过点A作垂直于y轴,垂足为点C,则的面积为( )
A.1 B. C.2 D.4
5.已知反比例函数的图象经过点,则这个函数的图象位于( )
A.第一、三象限 B.第二、三象限 C.第二、四象限 D.第三、四象限
6.如图,反比例函数和一次函数的图象交于A、B两点,且点A、B的横坐标分别为2和.通过观察图象,则不等式的解集是( )
A. B.或
C.或 D.
7.若点,,在反比例函数的图象上,则下列结论正确的是( )
A. B. C. D.
8.下列各点在反比例函数的图象上的是( )
A. B. C. D.
9.如图,点A在双曲线上,点B在双曲线上,且轴,点C和点D在x轴上,若四边形为矩形,则矩形的面积为( ).
A.1 B.2 C.3 D.
10.某车从甲地到乙地,行驶全程所需的时间与平均速度之间的反比例函数关系如图,当车速为80千米/时,则需要3小时能行驶全程.若该路段行车速度不能超过,则行车时间应控制在()
A.至多2.4小时 B.小于2.4小时 C.至少2.4小时 D.大于2.4小时
评卷人得分
二、填空题
11.如图,网格(每个小正方形的边长为1)中有,,,,,,,,九个格点,点的坐标为,反比例函数的表达式为.
(1)若反比例函数的图像过点,则它必过点 ;
(2)在九个格点中,若只有1个在反比例函数图像的上方,则的整数值有 个.
12.如图,点在反比例函数的图象上,,分别垂直于x轴、y轴,点D在位于右侧的反比例函数的图象上,,分别垂直于x轴、,若四边形为正方形,则这个正方形的面积等于 .
13.双曲线与直线相交于点和B,则点B坐标是 .
14.如图,在平面直角坐标系中,为直角三角形,,,.若反比例函数的图象经过上的点C,交于点D,且,则 .
15.如图,已知双曲线经过直角三角形斜边的中点D,且与直角边相交于点C.若点B的坐标为,则的面积为 .
16.如图, 点 A 是反比例函数的图象上的一点, 过点 A 作轴, 垂足为B, 点 C 为y轴上的 点, 连接,则的面积为 .
评卷人得分
三、问答题
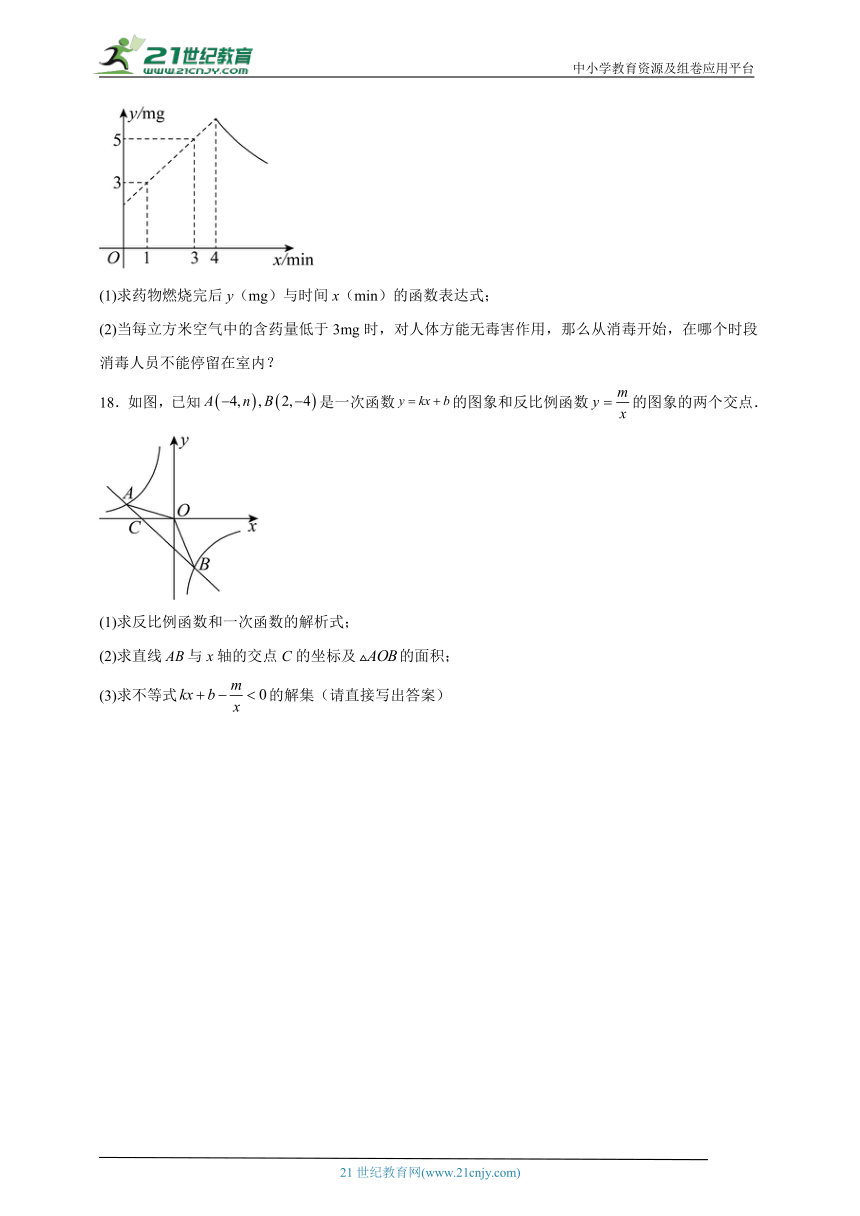
17.2023年11月份,由于病毒性流传性疾病比较严重,桥区某中学“红马甲”爱心互助队对“星光养老院”进行药物消毒,已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与时间x(min)之间成一次函数关系;燃烧完后y(mg)与时间x(min)之间成反比例函数关系.根据图象解答下列问题:
(1)求药物燃烧完后y(mg)与时间x(min)的函数表达式;
(2)当每立方米空气中的含药量低于3mg时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在室内?
18.如图,已知是一次函数的图象和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线与x轴的交点C的坐标及的面积;
(3)求不等式的解集(请直接写出答案)
参考答案:
1.A
【分析】此题主要考查了反比例函数图像上点的坐标特征,正确得出的符号是解题关键.
直接利用反比例函数的性质得出,进而求出答案.
【详解】反比例函数的图象上有两点、,
反比例函数的图象经过第二、四象限,
,
.
故选:A
2.A
【分析】本题考查了反比例函数的性质、一次函数的性质以及二次函数的性质,分析四个选项中得函数解析式,根据系数的正负结合各函数的性质即可得出其增减性,由此即可得出结论.
【详解】解:A、中,
∴函数的图象在第二、四象限内y随着x的增大而增大;
B、中,且图象关于轴对称,
∴函数的图象,当时,在第一、第四象限y随着x的增大而增大,当时,在第二、三象限y随着x的增大而减小;
C、中,
∴函数的图象在第一、三象限内y随着x的增大而减小;
D、中,,
∴函数的图象在第二、三、四象限内y随着x的增大而减小.
故选:A.
3.A
【分析】本题考查了一次函数与反比例函数的交点问题,等腰三角形的判定和性质,掌握一次函数和反比例函数的图象和性质是解题关键.过点作轴于点,过点作轴于点,由正比例函数和反比例函数的性质可知,、两点关于原点对称,设,则,,得到,进而得到,再利用等腰三角形三线合一的性质,得到,进而得到,即可求出k的值.
【详解】解:过点作轴于点,过点作轴于点,
函数与反比例函数的图象都关于原点对称,
、两点关于原点对称,
设,则,,
,
,
,
,
,轴,
,
,
,
,
,
故选:A.
4.D
【分析】本题主要考查反比例函数k的几何意义,熟练掌握反比例函数k的几何意义是解题的关键.由题意易得点A、B关于原点对称,则点O为的中点,则有和的面积相等,由反比例函数的几何意义可得的面积为2,进而问题可求解.
【详解】解:由函数与的图象交于A,B两点,则有点A、B关于原点对称;
∴点O为的中点;
∴;
∵轴,
∴由反比例函数k的几何意义可得;
∴;
故选:D.
5.A
【分析】本题考查了反比例函数的性质:当时,图象位于一、三象限;当时,图象位于二、四象限.还考查了待定系数法求函数解析式.设反比例函数解析式为,根据待定系数法求出的值,即可判断.
【详解】解:设反比例函数解析式为,
∵反比例函数的图象经过点,
∴
∴这个函数的图象位于第一、三象限
故选:A.
6.C
【分析】本题考查了一次函数与反比例函数的交点问题,以及运用图象法解决取值范围等问题,反比例函数和一次函数的图象交于A、B两点,且点A、B的横坐标分别为2和.即可得时的的范围.
【详解】解:∵反比例函数和一次函数的图象交于A、B两点,且点A、B的横坐标分别为2和.
∴则不等式的解集是或
故选:C
7.B
【分析】考查反比例函数图象上点的坐标特征,根据反比例函数的比例系数的符号可得反比例函数所在象限为一、三,其中在第三象限的点的纵坐标总小于在第一象限的纵坐标,进而判断在同一象限内的点B和点C的纵坐标的大小即可.
【详解】解:∵反比例函数的比例系数为,
∴图象的两个分支在一、三象限,且在每个象限内,y随x的增大而减小,
∵第三象限的点的纵坐标总小于在第一象限的纵坐标,点在第三象限,点B、C在第一象限,
∴最小,
∵,,,y随x的增大而减小,
∴,
∴.
故选:B.
8.B
【分析】本题主要考查反比例函数图象的性质,将点代入反比例函数进行计算即可求解,掌握根据反比例函数自变量的值求函数值的计算方法是解题的关键.
【详解】解:、反比例函数,当时,,则不在反比例函数图象上,不符合题意;
、反比例函数,当时,,则在反比例函数图象上,符合题意;
、反比例函数,当时,,则不在反比例函数图象上,不符合题意;
、反比例函数,当时,,则不在反比例函数图象上,不符合题意;
故选:.
9.B
【分析】本题主要考查反比例函数的应用,根据是矩形,点与点纵坐标相等,与点横坐标相等,可设出点、、的坐标,用坐标之差表示出矩形的边长,相乘即可求解.解答本题的关键在于用坐标之差表示出矩形边长.
【详解】解:∵四边形为矩形,
∴点与点纵坐标相等,点与点横坐标相等,
又∵点A在双曲线上,点B在双曲线上
∴设,,,
则用坐标之差表示:
,,
.
故选:B.
10.C
【分析】本题考查了反比例函数的应用,找出等量关系是解决此题的关键.
依据行程问题中的关系:时间=路程:速度,即可得到列车行驶完全程所需的时间与行驶的平均速度之间的关系式,把代入即可得到答案.
【详解】设列车行驶完全程所需的时间与行驶的平均速度之间的关系式为,
把时,代入得:,
∴,
∴列车行驶完全程所需的时间与行驶的平均速度之间的关系式为,当时,即,
根据图象若该路段行车速度不能超过,则行车时间应控制在至少2.4小时,
故选:C.
11.
【分析】本题主要考查了反比例函数图像和性质,理解反比例函数的图像和性质是解题的关键.
(1)先求出反比例函数解析式,然后代入检验即可;
(2)根据题意确定出系数k的取值范围即可解题.
【详解】(1)解:∵点的坐标为,
∴,,,,,,,,
把代入得,
∴,
把,,,,,,,代入,
符合的为点,
故答案为:;
(2)∵只有1个在反比例函数图像的上方,
∴点在上方,点B和点F在图象下方或在图像上,
故k的取值范围为:,
∴整数为,共个,
故答案为:.
12.
【分析】本题考查的是求解反比例函数解析式,反比例函数的性质,一元二次方程的解法,如图,延长交轴于,求解反比例函数为:,证明,设正方形的边长为,可得,再解方程可得答案.熟练的利用图形面积建立方程是解本题的关键.
【详解】解:如图,延长交轴于,
∵点在反比例函数的图象上,
∴,
∴反比例函数为:,
∴,
∴,
设正方形的边长为,,
∴,,
∴,
整理得,
解得:,(不符合题意,舍去),
∴正方形的面积为.
故答案为:.
13.
【分析】本题是反比例函数与一次函数的交点问题,考查了反比例函数图象上点的坐标特征,待定系数法求一次函数的解析式,求得点的坐标是解题的关键.
由反比例函数解析式求得点的坐标,然后根据反比例函数的对称性即可求得点B坐标.
【详解】解:把代入得,,
解得,
∴点,
则点B坐标是,
故答案为:.
14./
【分析】本题考查了反比例函数与几何的综合题,熟知直角三角形中的角所对的直角边是斜边的一半,熟练掌握勾股定理,求出点C的坐标是此题的关键.先根据直角三角形中的角所对的直角边是斜边的一半求出,再根据勾股定理求出,在中求出,最后根据求出点C的坐标,利用待定系数法求出k的值即可.
【详解】解:过点A作于点E,过点C作于点F,
∵,,.
∴
由勾股定理得
在中,,,
∴
由勾股定理得
∵,
∴
∴,,
∵点C在第一象限,
∴点C的坐标是
∵反比例函数的图象经过上的点C,
∴
故答案为:.
15.3
【分析】本题考查了线段的中点公式,待定系数法求反比例函数解析式,反比例函数的几何意义,先根据中点公式求出点D的坐标,再用待定系数法求出反比例函数解析式,然后根据反比例函数的几何意义求解即可.
【详解】解:∵点B的坐标为,双曲线经过直角三角形斜边的中点D,
∴点D的坐标为,
把代入得,,
∴.
故答案为:3.
16.3
【分析】本题考查了反比例函数k的几何意义,熟记“反比函数上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积等于k的绝对值”.
【详解】解:过A作轴,如图:
由反比例函数与x轴、y轴所围成的矩形面积等于k的绝对值可得:
,
,
故答案为:3.
17.(1);
(2)从消毒开始,第1分钟到第8分钟学生不能停留在室内.
【分析】本题主要考查了一次函数与反比例函数的实际应用,正确求出对应的函数解析式是解题的关键.
(1)利用待定系数法先求药物燃烧时与时间的函数表达式,再用待定系数法求药物燃烧完后与时间的函数表达式即可;
(2)分别求出药物燃烧时和药物燃烧后,时,x的值即可得到答案.
【详解】(1)解:设药物燃烧时y关于x的函数表达式为,
把和代入,得:
,
解得:,
∴药物燃烧时y关于x的函数表达式为,
当时,,
设药物燃烧后y关于x的函数表达式为,
把代入,
∴,
∴,
∴药物燃烧后y关于x的函数表达式为;
(2)解:对于,当时,
解得:;
对于,当时,
解得:,
答:从消毒开始,第1分钟到第8分钟学生不能停留在室内.
18.(1),
(2)6
(3)或
【分析】本题考查了一次函数和反比例函数的综合问题,以及和不等式相结合的问题,正确理解函数的图象的坐标,函数与自变量的关系是解决本题的关键.
(1)将代入,即可得到m,从而得到反比例函数解析式,然后将A、B代入,即可得到一次函数的解析式;
(2)在一次函数上,当时,即可得到的坐标,从而得到的长,然后由求出的面积;
(3)根据图象即可求出的解析,即不等式的解集.
【详解】(1)解:反比例函数经过点,
,
,
将,代入反比例解析式得:,
,
将与坐标代入一次函数解析式得:
,
解得:,
.
(2)解:在直线中,当时,,
,即,
.
(3)解:由图象知:当或时,,
故不等式的解集是或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年 人教版(五四制)九年级上册 第二十九章 反比例函数 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.反比例函数的图象上有两点、,且,则m的取值范围是( ).
A. B. C. D.
2.下列函数的图像在每一个象限内,随着的增大而增大的是( )
A. B. C. D.
3.如图,在平面直角坐标系中,函数与反比例函数交于A、B两点,点C在x轴上,且,若,则k的值是( )
A. B.6 C. D.
4.如图所示,如果函数与的图象交于A,B两点,过点A作垂直于y轴,垂足为点C,则的面积为( )
A.1 B. C.2 D.4
5.已知反比例函数的图象经过点,则这个函数的图象位于( )
A.第一、三象限 B.第二、三象限 C.第二、四象限 D.第三、四象限
6.如图,反比例函数和一次函数的图象交于A、B两点,且点A、B的横坐标分别为2和.通过观察图象,则不等式的解集是( )
A. B.或
C.或 D.
7.若点,,在反比例函数的图象上,则下列结论正确的是( )
A. B. C. D.
8.下列各点在反比例函数的图象上的是( )
A. B. C. D.
9.如图,点A在双曲线上,点B在双曲线上,且轴,点C和点D在x轴上,若四边形为矩形,则矩形的面积为( ).
A.1 B.2 C.3 D.
10.某车从甲地到乙地,行驶全程所需的时间与平均速度之间的反比例函数关系如图,当车速为80千米/时,则需要3小时能行驶全程.若该路段行车速度不能超过,则行车时间应控制在()
A.至多2.4小时 B.小于2.4小时 C.至少2.4小时 D.大于2.4小时
评卷人得分
二、填空题
11.如图,网格(每个小正方形的边长为1)中有,,,,,,,,九个格点,点的坐标为,反比例函数的表达式为.
(1)若反比例函数的图像过点,则它必过点 ;
(2)在九个格点中,若只有1个在反比例函数图像的上方,则的整数值有 个.
12.如图,点在反比例函数的图象上,,分别垂直于x轴、y轴,点D在位于右侧的反比例函数的图象上,,分别垂直于x轴、,若四边形为正方形,则这个正方形的面积等于 .
13.双曲线与直线相交于点和B,则点B坐标是 .
14.如图,在平面直角坐标系中,为直角三角形,,,.若反比例函数的图象经过上的点C,交于点D,且,则 .
15.如图,已知双曲线经过直角三角形斜边的中点D,且与直角边相交于点C.若点B的坐标为,则的面积为 .
16.如图, 点 A 是反比例函数的图象上的一点, 过点 A 作轴, 垂足为B, 点 C 为y轴上的 点, 连接,则的面积为 .
评卷人得分
三、问答题
17.2023年11月份,由于病毒性流传性疾病比较严重,桥区某中学“红马甲”爱心互助队对“星光养老院”进行药物消毒,已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与时间x(min)之间成一次函数关系;燃烧完后y(mg)与时间x(min)之间成反比例函数关系.根据图象解答下列问题:
(1)求药物燃烧完后y(mg)与时间x(min)的函数表达式;
(2)当每立方米空气中的含药量低于3mg时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在室内?
18.如图,已知是一次函数的图象和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线与x轴的交点C的坐标及的面积;
(3)求不等式的解集(请直接写出答案)
参考答案:
1.A
【分析】此题主要考查了反比例函数图像上点的坐标特征,正确得出的符号是解题关键.
直接利用反比例函数的性质得出,进而求出答案.
【详解】反比例函数的图象上有两点、,
反比例函数的图象经过第二、四象限,
,
.
故选:A
2.A
【分析】本题考查了反比例函数的性质、一次函数的性质以及二次函数的性质,分析四个选项中得函数解析式,根据系数的正负结合各函数的性质即可得出其增减性,由此即可得出结论.
【详解】解:A、中,
∴函数的图象在第二、四象限内y随着x的增大而增大;
B、中,且图象关于轴对称,
∴函数的图象,当时,在第一、第四象限y随着x的增大而增大,当时,在第二、三象限y随着x的增大而减小;
C、中,
∴函数的图象在第一、三象限内y随着x的增大而减小;
D、中,,
∴函数的图象在第二、三、四象限内y随着x的增大而减小.
故选:A.
3.A
【分析】本题考查了一次函数与反比例函数的交点问题,等腰三角形的判定和性质,掌握一次函数和反比例函数的图象和性质是解题关键.过点作轴于点,过点作轴于点,由正比例函数和反比例函数的性质可知,、两点关于原点对称,设,则,,得到,进而得到,再利用等腰三角形三线合一的性质,得到,进而得到,即可求出k的值.
【详解】解:过点作轴于点,过点作轴于点,
函数与反比例函数的图象都关于原点对称,
、两点关于原点对称,
设,则,,
,
,
,
,
,轴,
,
,
,
,
,
故选:A.
4.D
【分析】本题主要考查反比例函数k的几何意义,熟练掌握反比例函数k的几何意义是解题的关键.由题意易得点A、B关于原点对称,则点O为的中点,则有和的面积相等,由反比例函数的几何意义可得的面积为2,进而问题可求解.
【详解】解:由函数与的图象交于A,B两点,则有点A、B关于原点对称;
∴点O为的中点;
∴;
∵轴,
∴由反比例函数k的几何意义可得;
∴;
故选:D.
5.A
【分析】本题考查了反比例函数的性质:当时,图象位于一、三象限;当时,图象位于二、四象限.还考查了待定系数法求函数解析式.设反比例函数解析式为,根据待定系数法求出的值,即可判断.
【详解】解:设反比例函数解析式为,
∵反比例函数的图象经过点,
∴
∴这个函数的图象位于第一、三象限
故选:A.
6.C
【分析】本题考查了一次函数与反比例函数的交点问题,以及运用图象法解决取值范围等问题,反比例函数和一次函数的图象交于A、B两点,且点A、B的横坐标分别为2和.即可得时的的范围.
【详解】解:∵反比例函数和一次函数的图象交于A、B两点,且点A、B的横坐标分别为2和.
∴则不等式的解集是或
故选:C
7.B
【分析】考查反比例函数图象上点的坐标特征,根据反比例函数的比例系数的符号可得反比例函数所在象限为一、三,其中在第三象限的点的纵坐标总小于在第一象限的纵坐标,进而判断在同一象限内的点B和点C的纵坐标的大小即可.
【详解】解:∵反比例函数的比例系数为,
∴图象的两个分支在一、三象限,且在每个象限内,y随x的增大而减小,
∵第三象限的点的纵坐标总小于在第一象限的纵坐标,点在第三象限,点B、C在第一象限,
∴最小,
∵,,,y随x的增大而减小,
∴,
∴.
故选:B.
8.B
【分析】本题主要考查反比例函数图象的性质,将点代入反比例函数进行计算即可求解,掌握根据反比例函数自变量的值求函数值的计算方法是解题的关键.
【详解】解:、反比例函数,当时,,则不在反比例函数图象上,不符合题意;
、反比例函数,当时,,则在反比例函数图象上,符合题意;
、反比例函数,当时,,则不在反比例函数图象上,不符合题意;
、反比例函数,当时,,则不在反比例函数图象上,不符合题意;
故选:.
9.B
【分析】本题主要考查反比例函数的应用,根据是矩形,点与点纵坐标相等,与点横坐标相等,可设出点、、的坐标,用坐标之差表示出矩形的边长,相乘即可求解.解答本题的关键在于用坐标之差表示出矩形边长.
【详解】解:∵四边形为矩形,
∴点与点纵坐标相等,点与点横坐标相等,
又∵点A在双曲线上,点B在双曲线上
∴设,,,
则用坐标之差表示:
,,
.
故选:B.
10.C
【分析】本题考查了反比例函数的应用,找出等量关系是解决此题的关键.
依据行程问题中的关系:时间=路程:速度,即可得到列车行驶完全程所需的时间与行驶的平均速度之间的关系式,把代入即可得到答案.
【详解】设列车行驶完全程所需的时间与行驶的平均速度之间的关系式为,
把时,代入得:,
∴,
∴列车行驶完全程所需的时间与行驶的平均速度之间的关系式为,当时,即,
根据图象若该路段行车速度不能超过,则行车时间应控制在至少2.4小时,
故选:C.
11.
【分析】本题主要考查了反比例函数图像和性质,理解反比例函数的图像和性质是解题的关键.
(1)先求出反比例函数解析式,然后代入检验即可;
(2)根据题意确定出系数k的取值范围即可解题.
【详解】(1)解:∵点的坐标为,
∴,,,,,,,,
把代入得,
∴,
把,,,,,,,代入,
符合的为点,
故答案为:;
(2)∵只有1个在反比例函数图像的上方,
∴点在上方,点B和点F在图象下方或在图像上,
故k的取值范围为:,
∴整数为,共个,
故答案为:.
12.
【分析】本题考查的是求解反比例函数解析式,反比例函数的性质,一元二次方程的解法,如图,延长交轴于,求解反比例函数为:,证明,设正方形的边长为,可得,再解方程可得答案.熟练的利用图形面积建立方程是解本题的关键.
【详解】解:如图,延长交轴于,
∵点在反比例函数的图象上,
∴,
∴反比例函数为:,
∴,
∴,
设正方形的边长为,,
∴,,
∴,
整理得,
解得:,(不符合题意,舍去),
∴正方形的面积为.
故答案为:.
13.
【分析】本题是反比例函数与一次函数的交点问题,考查了反比例函数图象上点的坐标特征,待定系数法求一次函数的解析式,求得点的坐标是解题的关键.
由反比例函数解析式求得点的坐标,然后根据反比例函数的对称性即可求得点B坐标.
【详解】解:把代入得,,
解得,
∴点,
则点B坐标是,
故答案为:.
14./
【分析】本题考查了反比例函数与几何的综合题,熟知直角三角形中的角所对的直角边是斜边的一半,熟练掌握勾股定理,求出点C的坐标是此题的关键.先根据直角三角形中的角所对的直角边是斜边的一半求出,再根据勾股定理求出,在中求出,最后根据求出点C的坐标,利用待定系数法求出k的值即可.
【详解】解:过点A作于点E,过点C作于点F,
∵,,.
∴
由勾股定理得
在中,,,
∴
由勾股定理得
∵,
∴
∴,,
∵点C在第一象限,
∴点C的坐标是
∵反比例函数的图象经过上的点C,
∴
故答案为:.
15.3
【分析】本题考查了线段的中点公式,待定系数法求反比例函数解析式,反比例函数的几何意义,先根据中点公式求出点D的坐标,再用待定系数法求出反比例函数解析式,然后根据反比例函数的几何意义求解即可.
【详解】解:∵点B的坐标为,双曲线经过直角三角形斜边的中点D,
∴点D的坐标为,
把代入得,,
∴.
故答案为:3.
16.3
【分析】本题考查了反比例函数k的几何意义,熟记“反比函数上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积等于k的绝对值”.
【详解】解:过A作轴,如图:
由反比例函数与x轴、y轴所围成的矩形面积等于k的绝对值可得:
,
,
故答案为:3.
17.(1);
(2)从消毒开始,第1分钟到第8分钟学生不能停留在室内.
【分析】本题主要考查了一次函数与反比例函数的实际应用,正确求出对应的函数解析式是解题的关键.
(1)利用待定系数法先求药物燃烧时与时间的函数表达式,再用待定系数法求药物燃烧完后与时间的函数表达式即可;
(2)分别求出药物燃烧时和药物燃烧后,时,x的值即可得到答案.
【详解】(1)解:设药物燃烧时y关于x的函数表达式为,
把和代入,得:
,
解得:,
∴药物燃烧时y关于x的函数表达式为,
当时,,
设药物燃烧后y关于x的函数表达式为,
把代入,
∴,
∴,
∴药物燃烧后y关于x的函数表达式为;
(2)解:对于,当时,
解得:;
对于,当时,
解得:,
答:从消毒开始,第1分钟到第8分钟学生不能停留在室内.
18.(1),
(2)6
(3)或
【分析】本题考查了一次函数和反比例函数的综合问题,以及和不等式相结合的问题,正确理解函数的图象的坐标,函数与自变量的关系是解决本题的关键.
(1)将代入,即可得到m,从而得到反比例函数解析式,然后将A、B代入,即可得到一次函数的解析式;
(2)在一次函数上,当时,即可得到的坐标,从而得到的长,然后由求出的面积;
(3)根据图象即可求出的解析,即不等式的解集.
【详解】(1)解:反比例函数经过点,
,
,
将,代入反比例解析式得:,
,
将与坐标代入一次函数解析式得:
,
解得:,
.
(2)解:在直线中,当时,,
,即,
.
(3)解:由图象知:当或时,,
故不等式的解集是或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
