第十四章 平面直角坐标系单元测试卷(含解析)
文档属性
| 名称 | 第十四章 平面直角坐标系单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 845.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 05:48:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年 人教版(五四制)七年级上册 第十四章 平面直角坐标系 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
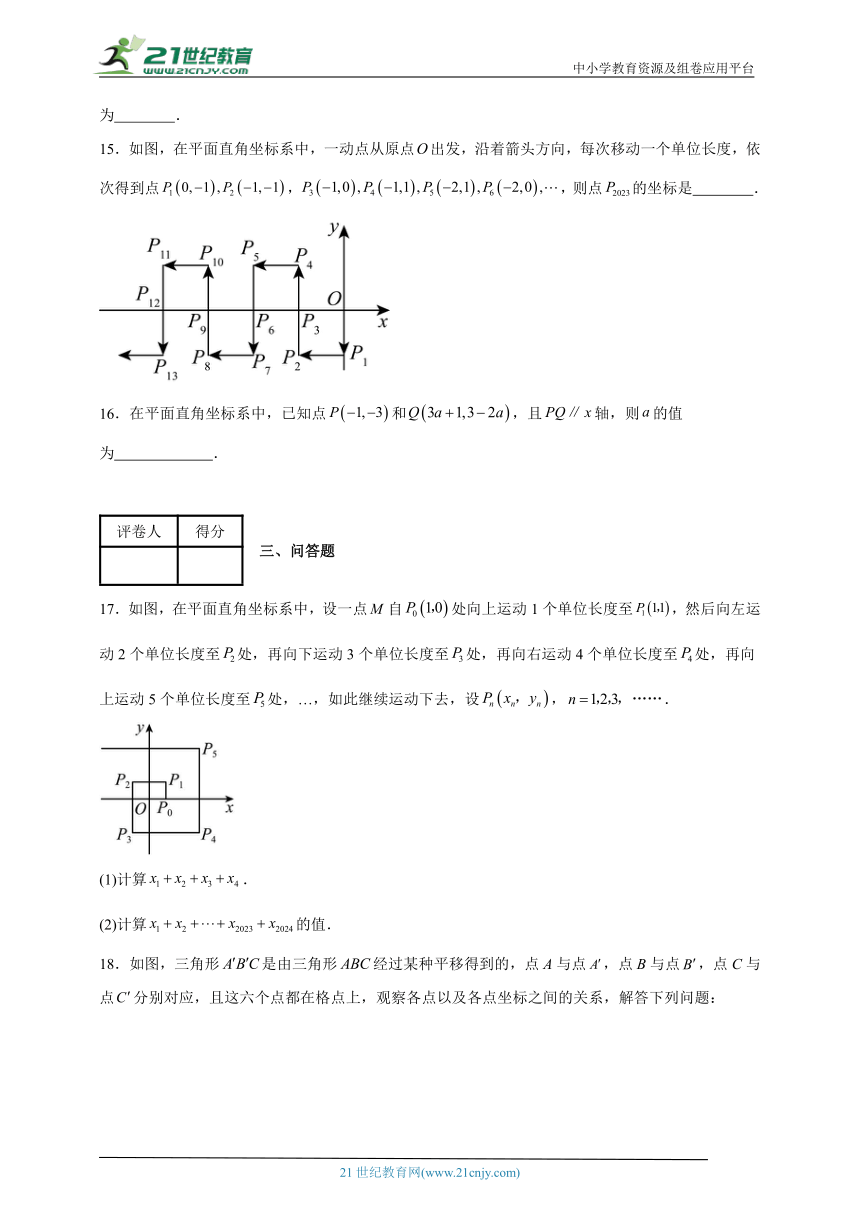
一、单选题
1.在平面直角坐标系中,下列各点在第二象限的是( )
A. B. C. D.
2.如图,这是一所学校的部分平面示意图,教学楼、实验楼和图书馆的位置都在边长为1的小正方形网格线的交点处,若教学楼位置的坐标是,实验楼位置的坐标是,则图书馆位置的坐标是( )
A. B. C. D.
3.已知点,那么点P关于x轴对称的的坐标是( )
A. B. C. D.
4.在平面直角坐标系中,点A的坐标为,则点A到x轴距离为( )
A. B.5 C. D.2
5.小军坐在教室的第3列第4行,小军的位置用表示,小红坐在第6行第1列,小红的位置可以用( )表示.
A. B. C. D.
6.已知点P的坐标为,且点P到两坐标轴距离相等,则a的值为( )
A. B. C.或 D.或3
7.在平面直角坐标系中,把点向右平移两个单位后,得到对应点的坐标是( )
A. B. C. D.
8.若点的坐标为,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知点,,点C在y正半轴上,且的面积是8,则点C的坐标为( )
A. B. C. D.
10.已知点的坐标为,点是轴上的一个动点,当、两点间的距离最短时,点的坐标为( )
A. B. C. D.
评卷人得分
二、填空题
11.如图所示,在平面直角坐标系中,动点按图中箭头所示方向依次运动,第1次运动到点,第2次运动到点,第3次运动到点,第4次运动到点,第5次运动到点…,按这样的运动规律,动点P第2023次运动到点的坐标为 .
12.已知点, 直线轴, 且, 则点N的坐标是
13.如图,已知村庄的坐标为,一辆汽车从原点出发沿轴向右行驶.行驶过程中汽车离村最近的距离为 .
14.在平面直角坐标系中,点在轴上,则的值为 ,点到轴的距离为 .
15.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头方向,每次移动一个单位长度,依次得到点,,则点的坐标是 .
16.在平面直角坐标系中,已知点和,且轴,则的值为 .
评卷人得分
三、问答题
17.如图,在平面直角坐标系中,设一点自处向上运动1个单位长度至,然后向左运动2个单位长度至处,再向下运动3个单位长度至处,再向右运动4个单位长度至处,再向上运动5个单位长度至处,…,如此继续运动下去,设,.
(1)计算.
(2)计算的值.
18.如图,三角形是由三角形经过某种平移得到的,点A与点,点B与点,点C与点分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点B和点的坐标,并说明三角形是由三角形经过怎样的平移得到的
(2)连接,直接写出与之间的数量关系;
(3)若点是三角形ABC内一点,它随三角形按(1)中方式平移后得到的对应点为点,求a和b的值.
参考答案:
1.B
【分析】本题考查了各象限内点的坐标的符号特征,根据第二象限内,点的横坐标小于零,纵坐标大于零,可得答案.
【详解】解:A.在第三象限,故本选项不合题意;
B.在第二象限,故本选项符合题意;
C.在第一象限,故本选项不合题意;
D.在第四象限,故本选项不合题意;
故选:B.
2.D
【分析】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.根据已知点坐标得出原点位置,进而得出答案.
【详解】解:如图所示:图书馆位置的坐标是.
故选:D.
3.B
【分析】本题主要考查关于x轴对称的点的坐标的特征.根据关于x轴对称的点的纵坐标互为相反数是解题的关键.
【详解】解:点关于x轴对称的的坐标是.
故选B.
4.B
【分析】本题主要考查了点到坐标轴的距离,熟知到x轴距离为纵坐标的绝对值,到y轴的距离为横坐标的绝对值是解题的关键.
【详解】解:∵在平面直角坐标系中,点A的坐标为,
∴点A到x轴距离为,
故选B.
5.D
【分析】此题考查了数对表示位置的方法.数对表示位置的方法是:第一个数字表示列,第二个数字表示行.
【详解】解:根据数对表示位置的方法可知:小红的位置用数对表示为:,
故选:D.
6.D
【分析】本题考查了坐标与图形性质;
根据到两坐标轴距离相等的点的横纵坐标相等或互为相反数列式计算即可.
【详解】解:∵点到两坐标轴距离相等,
∴或,
解得:或,
故选:D.
7.B
【分析】此题考查了点的坐标变化和平移之间的联系,平移时点的坐标变化规律是“上加下减,左减右加”.据此求解即可.
【详解】解:把点向右平移两个单位后,得到对应点的坐标是,即
故选:B.
8.C
【分析】本题主要考查了判断点所在的象限,熟知每个象限内点的坐标特点是解题的关键:第一象限;第二象限;第三象限;第四象限.
【详解】解:∵点的坐标为,,
∴点在第三象限,
故选C.
9.C
【分析】此题主要考查坐标系中的坐标与图形,根据点A和点B在x轴上,距离可用横坐标之差的绝对值求出,C点在y轴的正半轴上,用面积列等式求解即可.
【详解】解:点C在y轴的正半轴上,点和点在x轴上,
,
的面积为8,得
,
解得,
点,
故选:C.
10.D
【分析】此题考查了点的坐标、垂线段最短,根据当轴于点时,、两点间的距离最短,即可得到答案,熟练掌握点的坐标规律是解题的关键.
【详解】∵点的坐标为,点在轴上,
∴当轴于点时,、两点间的距离最短,
此时点与点的横坐标相同,
∴点的坐标是,
故选:.
11.
【分析】此题考查了图形坐标的规律,正确理解图形得到点P的运动规律并应用是解题的关键.
根据图形分析点P的运动规律:,,的横坐标为2022,纵坐标每四次为一个循环,即可得到答案.
【详解】解:第1次运动到点,第2次运动到点,第3次运动到点,第4次运动到点,第5次运动到点…,
∴每四次为一个循环,,
∴点的纵坐标为,
而,,与横坐标相差1,
∴的横坐标为2021,的横坐标为2022,
故答案为:.
12.或/或
【分析】本题考查了平面直角坐标系,根据平行于y的直线上的点横坐标相同,然后分情况讨论即可.熟知平行于y的直线上的点横坐标相同是解本题的关键.
【详解】解:∵,轴,
∴点N的纵坐标为2,
∵,
∴点N的横坐标为或,
∴点N的坐标为或,
故答案为:或.
13.4
【分析】本题主要考查了平面直角坐标系中点到坐标轴的距离,垂线段最短,根据垂线段最短得出当汽车运动的位置与点A的连线与x轴垂直时,汽车离A村最近的距离最小,再根据点到x轴的距离等于纵坐标的绝对值,求出这个最小距离即可.
【详解】解:∵村庄的坐标为,
∴点A到轴的距离为,
又∵垂线段最短,
∴行驶过程中汽车离A村最近的距离为4.
故答案为:4.
14. /
【分析】本题考查了平面直角坐标系中点的坐标特征,熟练掌握轴上的点纵坐标都为零是解答本题的关键.
【详解】解:点在轴上,
,
解得:,
∴,
∴点到轴的距离为.
故答案为:;.
15.
【分析】本题主要考查了点的坐标方面规律问题的解决能力,关键是能准确理解题意确定出点移动的规律.由题意得该点按6次一循环的规律移动,用2023除以6,再确定商和余数即可.
【详解】解:由题意该点按“下→左→上→上→左→下”的方向每6次一循环移动的规律移动,且每移动一个循环向左移动2个单位长度,
∵,
∴点的横坐标为,且点的纵坐标与的纵坐标相同都是,
即点的坐标是.
故答案为:.
16.3
【分析】本题主要考查了坐标与图形,根据平行于x轴的直线上的点纵坐标都相等得到,解之即可得到答案.
【详解】解:∵点和,且轴,
∴,
∴,
故答案为:3.
17.(1)2
(2)1012
【分析】此题主要考查了点的坐标特点,解决本题的关键是分析得到4个数相加的规律.
(1)根据各点横坐标、纵坐标的数据得出规律,进而得出答案即可;
(2)经过观察分析可得每4个数的和为2,把2024个数分为506组,即可得到相应结果.
【详解】(1)解:由题意可知 ……
于是得到的值为1,,,3,
∴
(2)解:∵的值分别为3,,,,
∴;
∵,
,
…
,
∵
∴.
18.(1)B , ,平移方式:先向左平移3个单位长度,再向下平移3个单位长度;
(2)
(3)的值是3,的值是4
【分析】本题主要考查了坐标与图形,根据平移前后点的坐标判断平移方式,平移的性质,解题的关键在于能够熟练掌握点坐标平移的规律.
(1)根据点在坐标轴的位置得到点B的坐标为,点的坐标为, 由此即可得到平移方式;
(2)由平移的性质可得,则,再根据轴,得到,则;
(3)根据平移方式可以得到,,由此求解即可.
【详解】(1)解:由题图知,点B的坐标为,点的坐标为,,
∴三角形是由三角形先向左平移3个单位长度,再向下平移3个单位长度得到的.
(2)与之间的数量关系为,
解:由平移的性质可得,
∴,
∵点B的坐标为,点的坐标为,
∴轴,
∴,
∴,
∴与之间的数量关系为;
(3)解:由平移方式可得是点先向左平移3个单位长度,再向下平移3个单位长度得到的,
∴,,,
∴,,
∴的值是3,的值是4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年 人教版(五四制)七年级上册 第十四章 平面直角坐标系 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.在平面直角坐标系中,下列各点在第二象限的是( )
A. B. C. D.
2.如图,这是一所学校的部分平面示意图,教学楼、实验楼和图书馆的位置都在边长为1的小正方形网格线的交点处,若教学楼位置的坐标是,实验楼位置的坐标是,则图书馆位置的坐标是( )
A. B. C. D.
3.已知点,那么点P关于x轴对称的的坐标是( )
A. B. C. D.
4.在平面直角坐标系中,点A的坐标为,则点A到x轴距离为( )
A. B.5 C. D.2
5.小军坐在教室的第3列第4行,小军的位置用表示,小红坐在第6行第1列,小红的位置可以用( )表示.
A. B. C. D.
6.已知点P的坐标为,且点P到两坐标轴距离相等,则a的值为( )
A. B. C.或 D.或3
7.在平面直角坐标系中,把点向右平移两个单位后,得到对应点的坐标是( )
A. B. C. D.
8.若点的坐标为,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知点,,点C在y正半轴上,且的面积是8,则点C的坐标为( )
A. B. C. D.
10.已知点的坐标为,点是轴上的一个动点,当、两点间的距离最短时,点的坐标为( )
A. B. C. D.
评卷人得分
二、填空题
11.如图所示,在平面直角坐标系中,动点按图中箭头所示方向依次运动,第1次运动到点,第2次运动到点,第3次运动到点,第4次运动到点,第5次运动到点…,按这样的运动规律,动点P第2023次运动到点的坐标为 .
12.已知点, 直线轴, 且, 则点N的坐标是
13.如图,已知村庄的坐标为,一辆汽车从原点出发沿轴向右行驶.行驶过程中汽车离村最近的距离为 .
14.在平面直角坐标系中,点在轴上,则的值为 ,点到轴的距离为 .
15.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头方向,每次移动一个单位长度,依次得到点,,则点的坐标是 .
16.在平面直角坐标系中,已知点和,且轴,则的值为 .
评卷人得分
三、问答题
17.如图,在平面直角坐标系中,设一点自处向上运动1个单位长度至,然后向左运动2个单位长度至处,再向下运动3个单位长度至处,再向右运动4个单位长度至处,再向上运动5个单位长度至处,…,如此继续运动下去,设,.
(1)计算.
(2)计算的值.
18.如图,三角形是由三角形经过某种平移得到的,点A与点,点B与点,点C与点分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点B和点的坐标,并说明三角形是由三角形经过怎样的平移得到的
(2)连接,直接写出与之间的数量关系;
(3)若点是三角形ABC内一点,它随三角形按(1)中方式平移后得到的对应点为点,求a和b的值.
参考答案:
1.B
【分析】本题考查了各象限内点的坐标的符号特征,根据第二象限内,点的横坐标小于零,纵坐标大于零,可得答案.
【详解】解:A.在第三象限,故本选项不合题意;
B.在第二象限,故本选项符合题意;
C.在第一象限,故本选项不合题意;
D.在第四象限,故本选项不合题意;
故选:B.
2.D
【分析】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.根据已知点坐标得出原点位置,进而得出答案.
【详解】解:如图所示:图书馆位置的坐标是.
故选:D.
3.B
【分析】本题主要考查关于x轴对称的点的坐标的特征.根据关于x轴对称的点的纵坐标互为相反数是解题的关键.
【详解】解:点关于x轴对称的的坐标是.
故选B.
4.B
【分析】本题主要考查了点到坐标轴的距离,熟知到x轴距离为纵坐标的绝对值,到y轴的距离为横坐标的绝对值是解题的关键.
【详解】解:∵在平面直角坐标系中,点A的坐标为,
∴点A到x轴距离为,
故选B.
5.D
【分析】此题考查了数对表示位置的方法.数对表示位置的方法是:第一个数字表示列,第二个数字表示行.
【详解】解:根据数对表示位置的方法可知:小红的位置用数对表示为:,
故选:D.
6.D
【分析】本题考查了坐标与图形性质;
根据到两坐标轴距离相等的点的横纵坐标相等或互为相反数列式计算即可.
【详解】解:∵点到两坐标轴距离相等,
∴或,
解得:或,
故选:D.
7.B
【分析】此题考查了点的坐标变化和平移之间的联系,平移时点的坐标变化规律是“上加下减,左减右加”.据此求解即可.
【详解】解:把点向右平移两个单位后,得到对应点的坐标是,即
故选:B.
8.C
【分析】本题主要考查了判断点所在的象限,熟知每个象限内点的坐标特点是解题的关键:第一象限;第二象限;第三象限;第四象限.
【详解】解:∵点的坐标为,,
∴点在第三象限,
故选C.
9.C
【分析】此题主要考查坐标系中的坐标与图形,根据点A和点B在x轴上,距离可用横坐标之差的绝对值求出,C点在y轴的正半轴上,用面积列等式求解即可.
【详解】解:点C在y轴的正半轴上,点和点在x轴上,
,
的面积为8,得
,
解得,
点,
故选:C.
10.D
【分析】此题考查了点的坐标、垂线段最短,根据当轴于点时,、两点间的距离最短,即可得到答案,熟练掌握点的坐标规律是解题的关键.
【详解】∵点的坐标为,点在轴上,
∴当轴于点时,、两点间的距离最短,
此时点与点的横坐标相同,
∴点的坐标是,
故选:.
11.
【分析】此题考查了图形坐标的规律,正确理解图形得到点P的运动规律并应用是解题的关键.
根据图形分析点P的运动规律:,,的横坐标为2022,纵坐标每四次为一个循环,即可得到答案.
【详解】解:第1次运动到点,第2次运动到点,第3次运动到点,第4次运动到点,第5次运动到点…,
∴每四次为一个循环,,
∴点的纵坐标为,
而,,与横坐标相差1,
∴的横坐标为2021,的横坐标为2022,
故答案为:.
12.或/或
【分析】本题考查了平面直角坐标系,根据平行于y的直线上的点横坐标相同,然后分情况讨论即可.熟知平行于y的直线上的点横坐标相同是解本题的关键.
【详解】解:∵,轴,
∴点N的纵坐标为2,
∵,
∴点N的横坐标为或,
∴点N的坐标为或,
故答案为:或.
13.4
【分析】本题主要考查了平面直角坐标系中点到坐标轴的距离,垂线段最短,根据垂线段最短得出当汽车运动的位置与点A的连线与x轴垂直时,汽车离A村最近的距离最小,再根据点到x轴的距离等于纵坐标的绝对值,求出这个最小距离即可.
【详解】解:∵村庄的坐标为,
∴点A到轴的距离为,
又∵垂线段最短,
∴行驶过程中汽车离A村最近的距离为4.
故答案为:4.
14. /
【分析】本题考查了平面直角坐标系中点的坐标特征,熟练掌握轴上的点纵坐标都为零是解答本题的关键.
【详解】解:点在轴上,
,
解得:,
∴,
∴点到轴的距离为.
故答案为:;.
15.
【分析】本题主要考查了点的坐标方面规律问题的解决能力,关键是能准确理解题意确定出点移动的规律.由题意得该点按6次一循环的规律移动,用2023除以6,再确定商和余数即可.
【详解】解:由题意该点按“下→左→上→上→左→下”的方向每6次一循环移动的规律移动,且每移动一个循环向左移动2个单位长度,
∵,
∴点的横坐标为,且点的纵坐标与的纵坐标相同都是,
即点的坐标是.
故答案为:.
16.3
【分析】本题主要考查了坐标与图形,根据平行于x轴的直线上的点纵坐标都相等得到,解之即可得到答案.
【详解】解:∵点和,且轴,
∴,
∴,
故答案为:3.
17.(1)2
(2)1012
【分析】此题主要考查了点的坐标特点,解决本题的关键是分析得到4个数相加的规律.
(1)根据各点横坐标、纵坐标的数据得出规律,进而得出答案即可;
(2)经过观察分析可得每4个数的和为2,把2024个数分为506组,即可得到相应结果.
【详解】(1)解:由题意可知 ……
于是得到的值为1,,,3,
∴
(2)解:∵的值分别为3,,,,
∴;
∵,
,
…
,
∵
∴.
18.(1)B , ,平移方式:先向左平移3个单位长度,再向下平移3个单位长度;
(2)
(3)的值是3,的值是4
【分析】本题主要考查了坐标与图形,根据平移前后点的坐标判断平移方式,平移的性质,解题的关键在于能够熟练掌握点坐标平移的规律.
(1)根据点在坐标轴的位置得到点B的坐标为,点的坐标为, 由此即可得到平移方式;
(2)由平移的性质可得,则,再根据轴,得到,则;
(3)根据平移方式可以得到,,由此求解即可.
【详解】(1)解:由题图知,点B的坐标为,点的坐标为,,
∴三角形是由三角形先向左平移3个单位长度,再向下平移3个单位长度得到的.
(2)与之间的数量关系为,
解:由平移的性质可得,
∴,
∵点B的坐标为,点的坐标为,
∴轴,
∴,
∴,
∴与之间的数量关系为;
(3)解:由平移方式可得是点先向左平移3个单位长度,再向下平移3个单位长度得到的,
∴,,,
∴,,
∴的值是3,的值是4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
