第十二章 相交线与平行线单元测试卷(含解析)
文档属性
| 名称 | 第十二章 相交线与平行线单元测试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 931.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 05:46:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
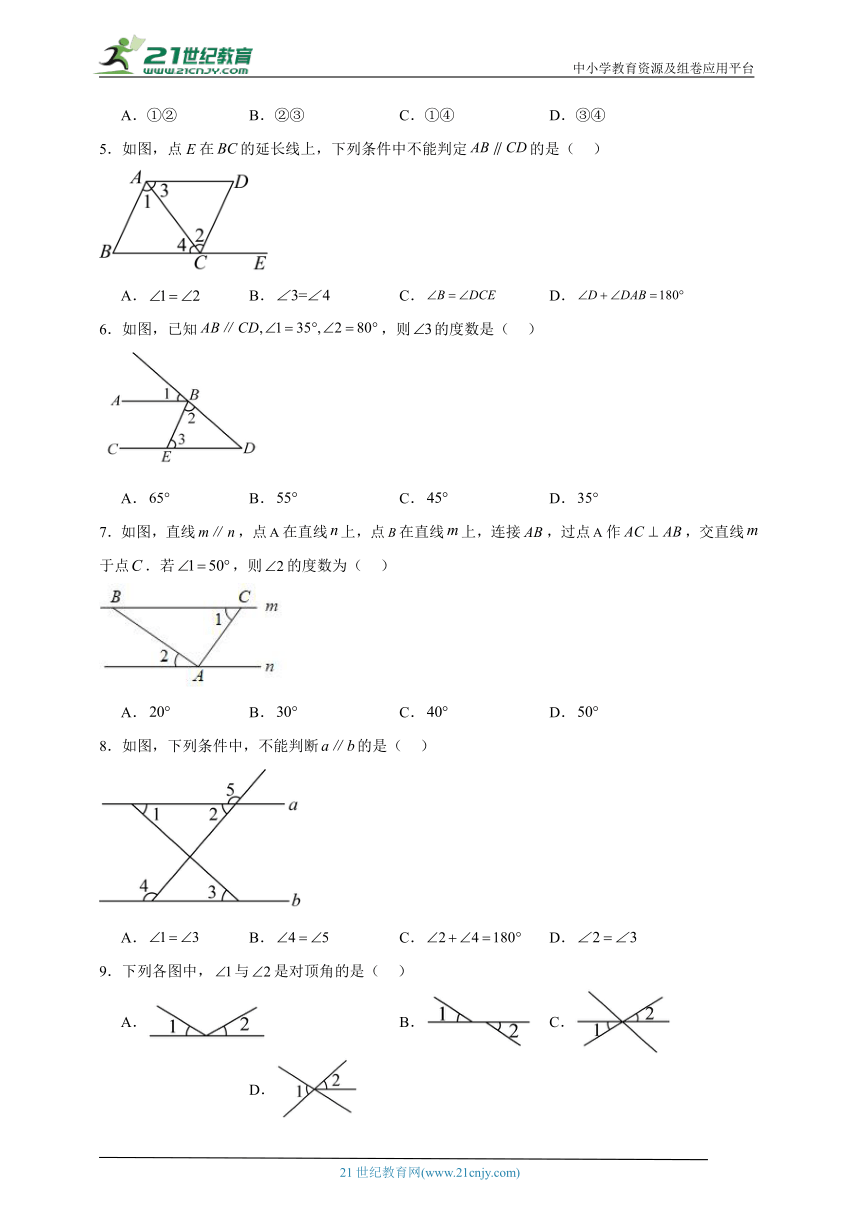
2023-2024学年 人教版(五四制)七年级上册 第十二章 相交线与平行线 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,,EF分别截于点E,F,连结,则下列结论错误的是( )
AI
A. B.
C. D.
2.如图,能推断的是( )
A. B. C. D.
3.如图,直线,和分别为直线与直线和相交所成的角.如果,那么的度数为( )
A. B. C. D.
4.下列现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上测量某个同学的跳远成绩;④工人砌墙时,先在两端立桩拉线,然后沿着线砌墙.其中,可以用“两点确定一条直线”来解释的现象是( )
A.①② B.②③ C.①④ D.③④
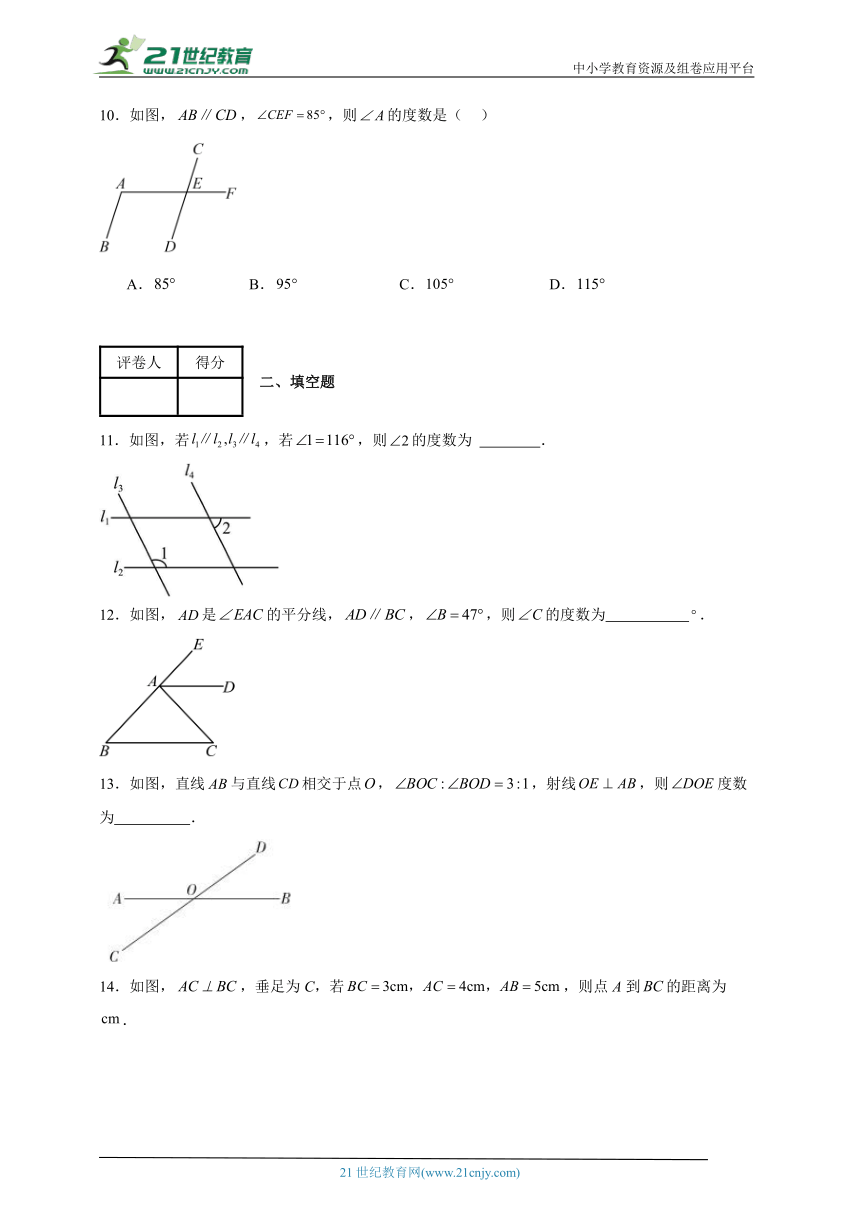
5.如图,点E在的延长线上,下列条件中不能判定的是( )
A. B. C. D.
6.如图,已知,则的度数是( )
A. B. C. D.
7.如图,直线,点在直线上,点在直线上,连接,过点作,交直线于点.若,则的度数为( )
A. B. C. D.
8.如图,下列条件中,不能判断的是( )
A. B. C. D.
9.下列各图中,与是对顶角的是( )
A. B. C. D.
10.如图,,,则的度数是( )
A. B. C. D.
评卷人得分
二、填空题
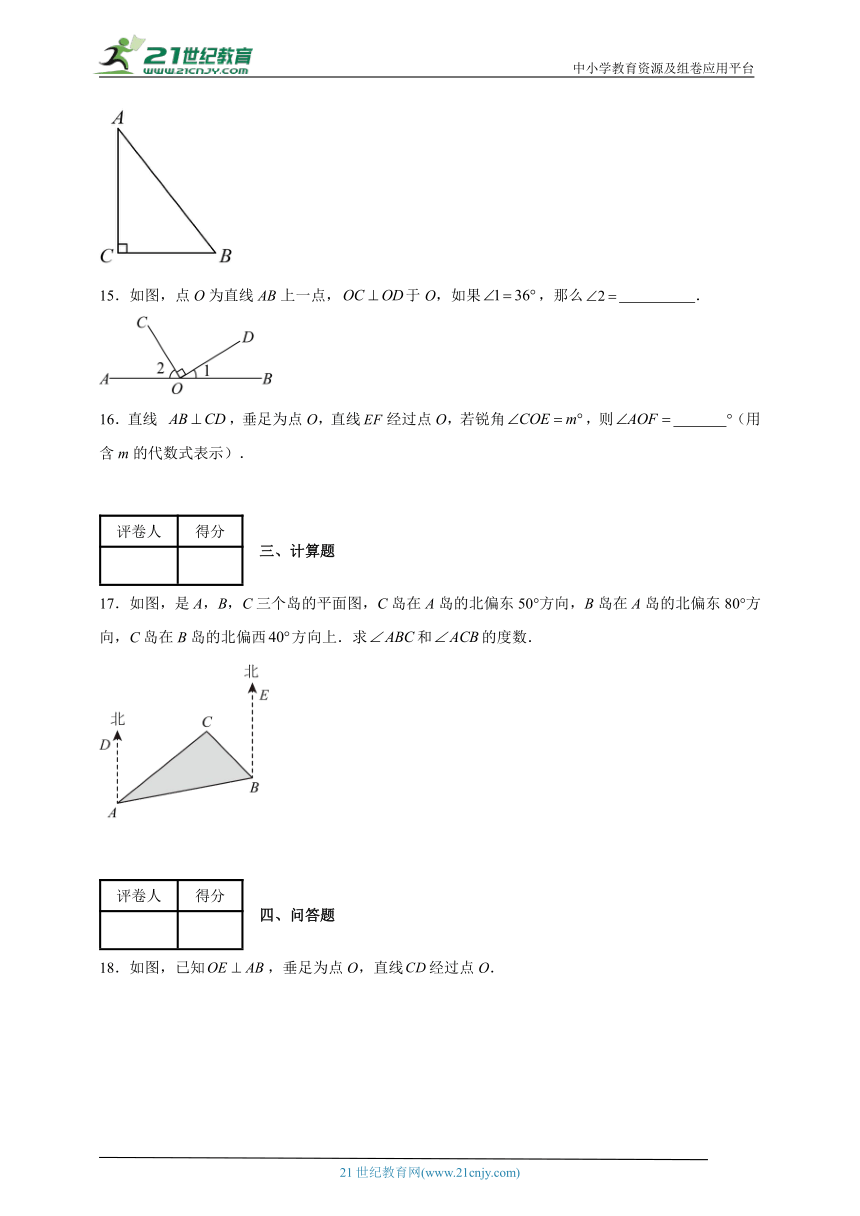
11.如图,若,若,则的度数为 .
12.如图,是的平分线,,,则的度数为 .
13.如图,直线与直线相交于点,,射线,则度数为 .
14.如图,,垂足为C,若,则点A到的距离为 .
15.如图,点O为直线AB上一点,于O,如果,那么 .
16.直线 ,垂足为点O,直线经过点O,若锐角,则 °(用含m的代数式表示).
评卷人得分
三、计算题
17.如图,是A,B,C三个岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西方向上.求和的度数.
评卷人得分
四、问答题
18.如图,已知,垂足为点O,直线经过点O.
(1)若,求的度数;
(2)若,求的度数;
(3)在(2)的条件下,过点O作,则 .(直接写出答案)
参考答案:
1.B
【分析】本题考查平行线的性质,解答的关键是熟记平行线的性质.利用平行线的性质对各项进行分析即可.
【详解】,
,
,
,故A结论正确,不符合题意;
,
,
,故C结论正确,不符合题意;
,
,,
,
,故D结论正确,不符合题意;
无法求得,故B结论错误,符合题意.
故选:B.
2.B
【分析】本题主要考查平行线的判定,“同位角相等,两直线平行”,“同旁内角互补两直线平行”,“内错角相等两直线平行”,直接根据判定定理判定即可.
【详解】解:A、∵,
∴,不能推出;
B、,
∴,故本选项B正确;
C、∵,
∴,
∴,不能推出;
D、∵,
∴,不能推出;
故选:B.
3.A
【分析】本题主要考查了平行线的性质、邻补角的定义,根据两直线平行,同位角相等得到,再由邻补角互补可得.
【详解】解:∵,,
∴,
∵,
∴,
故选A.
4.C
【分析】本题主要考查了两点确定一条直线,两点之间线段最短,点到直线的距离等等,熟练掌握两点确定一条直线的概念是解题的关键.
【详解】解:①用两根钉子就可以把一根木条固定在墙上,利用了两点确定一条直线,符合题意;
②把弯曲的公路改直,就能够缩短路程,利用“两点之间线段最短”,不符合题意;
③体育课上测量某个同学的跳远成绩,利用了点到直线的距离,不符合题意;
④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙,利用了两点确定一条直线,符合题意;
故选C.
5.B
【分析】此题主要考查了平行线的判定,根据平行线的判定定理同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行分别进行分析.关键是掌握平行线的判定定理.
【详解】解:,
,故选项A不合题意;
,
,不能判定,故选项B符合题意;
,
,故选项C不合题意;
∵,
,故选项D不合题意.
故选:B.
6.A
【分析】本题考查了平行线的性质,平角的定义,根据平行线的性质可得,即可求解.
【详解】解:∵,
∴,
故选:A.
7.C
【分析】本题考查了平行线的性质和垂线的定义,熟知:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.根据两直线平行,同旁内角互补得出,结合已知条件即可求出的度数.
【详解】解:如图所示,
∵,
∴,
∴
∵,
∴,
∵,
∴,
∴,
故选:C.
8.D
【分析】本题考查了平行线的判定,结合图形分析两角的位置关系,根据平行线的判定方法逐项判断即可,解题的关键是熟练掌握两直线平行的判定方法.
【详解】、由,根据内错角相等,两直线平行,可以判断,不符合题意;
、由,根据同位角相等,两直线平行,可以判断,不符合题意;
、由,根据同旁内角互补,两直线平行,可以判断,不符合题意;
、由,不可以判断,符合题意;
故选:.
9.C
【分析】本题考查了对顶角的定义,根据对顶角的定义判断即可.有一个公共点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角互为对顶角.
【详解】解:A、的两边不是的两边的反向延长线,与不是对顶角,故该选项不合题意;
B、的两边不是的两边的反向延长线,与不是对顶角,故该选项不符合题意;
C、的两边分别是的两边的反向延长线,与是对顶角,故该选项符合题意;
D、的两边不是的两边的反向延长线,与不是对顶角,故该选项不合题意.
故选:C.
10.B
【分析】本题考查了平行线的性质,邻补角的性质,熟练掌握根据邻补角互补求出的度数,再根据两直线平行,同位角相等得出,即可求出的度数.
【详解】解:,
,
,
,
故选:B.
11.64°/64度
【分析】本题考查平行线的性质.根据两直线平行同旁内角互补,同位角相等,是解题的关键.掌握平行线的性质,是解题的关键.
【详解】解:∵∥,,
∴,
∵,
∴.
故答案为:.
12.47
【分析】本题考查了角平分线的定义,平行线的性质.由平行线的性质,得到,,再根据角平分线的定义,得出,即可求出的度数.解题关键是掌握两直线平行,同位角相等,内错角相等,同旁内角互补.
【详解】解:,
,,
是的平分线,
,
,
,
,
故答案为:.
13.或
【分析】本题主要考查了几何图形中角度的计算,垂线的定义,邻补角互补,先根据邻补角互补结合已知条件得到,再分当射线在上方时,当射线在下方时,两种情况根据垂线的定义得到,再根据角之间的关系进行求解即可.
【详解】解:∵,,
∴,
如图所示,当射线在上方时,
∵,
∴,
∴;
如图所示,当射线在下方时,
∵,
∴,
∴;
综上所述,度数为或.
故答案为:或.
14.4
【分析】本题考查点到直线的距离,此题关键是理解点A到BC的距离是从点A向BC作垂线,所得的垂线段.根据点到直线的距离即可判断.
【详解】解:∵,垂足为C.
∴点A到的距离,即.
故答案为:4
15./54度
【分析】本题考查了角的计算,由平角的定义和垂直的定义可得的度数.把握图中角之间的关系是解题的关键.
【详解】解: ,
,
,,
故答案为:.
16.或
【分析】本题主要考查了对顶角的定义和性质,掌握其性质是解本题的关键.
对顶角的定义:有一个公共顶点,且一个角的两条边分别是另一个角的两条边的反向延长线,那么这两个角就叫做对顶角.根据题意,利用对顶角的性质通过计算解出答案.
【详解】由题意,需讨论以下两种情况:
①如图1
∵,
∴ ;
∵与是对顶角;
∴,
∴.
②如图2
∵,
∴;
∵与是对顶角,
∴,
∴.
综上:或.
故答案为:或.
17.;
【分析】本题主要考查了平行线的判定与性质,过点C作是解答本题的关键,先由,求得,从而可知;过点C作,利用平行线的传递性可知,再根据平行线的性质,求出,,即可得出答案.
【详解】解:由题意可知,,,
,
,
,
,
过点C作,
,
,
,
.
18.(1)
(2)
(3)或
【分析】本题考查的是垂直的性质,角平分线的定义,以及对顶角和邻补角.
(1)根据,得,由,得到与互余,从而得出结果;
(2)根据,得到,由即可求解;
(3)先过点O作,再分两种情况根据角的和差关系可求的度数.
【详解】(1)解:,
,
,
,
;
(2)解:,
,
,
,
,
;
(3)解:如图,当在下方时,则,
由(2)知,
;
如图,当在上方时,则,
由(2)知,
,
故答案为:或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年 人教版(五四制)七年级上册 第十二章 相交线与平行线 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,,EF分别截于点E,F,连结,则下列结论错误的是( )
AI
A. B.
C. D.
2.如图,能推断的是( )
A. B. C. D.
3.如图,直线,和分别为直线与直线和相交所成的角.如果,那么的度数为( )
A. B. C. D.
4.下列现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上测量某个同学的跳远成绩;④工人砌墙时,先在两端立桩拉线,然后沿着线砌墙.其中,可以用“两点确定一条直线”来解释的现象是( )
A.①② B.②③ C.①④ D.③④
5.如图,点E在的延长线上,下列条件中不能判定的是( )
A. B. C. D.
6.如图,已知,则的度数是( )
A. B. C. D.
7.如图,直线,点在直线上,点在直线上,连接,过点作,交直线于点.若,则的度数为( )
A. B. C. D.
8.如图,下列条件中,不能判断的是( )
A. B. C. D.
9.下列各图中,与是对顶角的是( )
A. B. C. D.
10.如图,,,则的度数是( )
A. B. C. D.
评卷人得分
二、填空题
11.如图,若,若,则的度数为 .
12.如图,是的平分线,,,则的度数为 .
13.如图,直线与直线相交于点,,射线,则度数为 .
14.如图,,垂足为C,若,则点A到的距离为 .
15.如图,点O为直线AB上一点,于O,如果,那么 .
16.直线 ,垂足为点O,直线经过点O,若锐角,则 °(用含m的代数式表示).
评卷人得分
三、计算题
17.如图,是A,B,C三个岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西方向上.求和的度数.
评卷人得分
四、问答题
18.如图,已知,垂足为点O,直线经过点O.
(1)若,求的度数;
(2)若,求的度数;
(3)在(2)的条件下,过点O作,则 .(直接写出答案)
参考答案:
1.B
【分析】本题考查平行线的性质,解答的关键是熟记平行线的性质.利用平行线的性质对各项进行分析即可.
【详解】,
,
,
,故A结论正确,不符合题意;
,
,
,故C结论正确,不符合题意;
,
,,
,
,故D结论正确,不符合题意;
无法求得,故B结论错误,符合题意.
故选:B.
2.B
【分析】本题主要考查平行线的判定,“同位角相等,两直线平行”,“同旁内角互补两直线平行”,“内错角相等两直线平行”,直接根据判定定理判定即可.
【详解】解:A、∵,
∴,不能推出;
B、,
∴,故本选项B正确;
C、∵,
∴,
∴,不能推出;
D、∵,
∴,不能推出;
故选:B.
3.A
【分析】本题主要考查了平行线的性质、邻补角的定义,根据两直线平行,同位角相等得到,再由邻补角互补可得.
【详解】解:∵,,
∴,
∵,
∴,
故选A.
4.C
【分析】本题主要考查了两点确定一条直线,两点之间线段最短,点到直线的距离等等,熟练掌握两点确定一条直线的概念是解题的关键.
【详解】解:①用两根钉子就可以把一根木条固定在墙上,利用了两点确定一条直线,符合题意;
②把弯曲的公路改直,就能够缩短路程,利用“两点之间线段最短”,不符合题意;
③体育课上测量某个同学的跳远成绩,利用了点到直线的距离,不符合题意;
④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙,利用了两点确定一条直线,符合题意;
故选C.
5.B
【分析】此题主要考查了平行线的判定,根据平行线的判定定理同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行分别进行分析.关键是掌握平行线的判定定理.
【详解】解:,
,故选项A不合题意;
,
,不能判定,故选项B符合题意;
,
,故选项C不合题意;
∵,
,故选项D不合题意.
故选:B.
6.A
【分析】本题考查了平行线的性质,平角的定义,根据平行线的性质可得,即可求解.
【详解】解:∵,
∴,
故选:A.
7.C
【分析】本题考查了平行线的性质和垂线的定义,熟知:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.根据两直线平行,同旁内角互补得出,结合已知条件即可求出的度数.
【详解】解:如图所示,
∵,
∴,
∴
∵,
∴,
∵,
∴,
∴,
故选:C.
8.D
【分析】本题考查了平行线的判定,结合图形分析两角的位置关系,根据平行线的判定方法逐项判断即可,解题的关键是熟练掌握两直线平行的判定方法.
【详解】、由,根据内错角相等,两直线平行,可以判断,不符合题意;
、由,根据同位角相等,两直线平行,可以判断,不符合题意;
、由,根据同旁内角互补,两直线平行,可以判断,不符合题意;
、由,不可以判断,符合题意;
故选:.
9.C
【分析】本题考查了对顶角的定义,根据对顶角的定义判断即可.有一个公共点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角互为对顶角.
【详解】解:A、的两边不是的两边的反向延长线,与不是对顶角,故该选项不合题意;
B、的两边不是的两边的反向延长线,与不是对顶角,故该选项不符合题意;
C、的两边分别是的两边的反向延长线,与是对顶角,故该选项符合题意;
D、的两边不是的两边的反向延长线,与不是对顶角,故该选项不合题意.
故选:C.
10.B
【分析】本题考查了平行线的性质,邻补角的性质,熟练掌握根据邻补角互补求出的度数,再根据两直线平行,同位角相等得出,即可求出的度数.
【详解】解:,
,
,
,
故选:B.
11.64°/64度
【分析】本题考查平行线的性质.根据两直线平行同旁内角互补,同位角相等,是解题的关键.掌握平行线的性质,是解题的关键.
【详解】解:∵∥,,
∴,
∵,
∴.
故答案为:.
12.47
【分析】本题考查了角平分线的定义,平行线的性质.由平行线的性质,得到,,再根据角平分线的定义,得出,即可求出的度数.解题关键是掌握两直线平行,同位角相等,内错角相等,同旁内角互补.
【详解】解:,
,,
是的平分线,
,
,
,
,
故答案为:.
13.或
【分析】本题主要考查了几何图形中角度的计算,垂线的定义,邻补角互补,先根据邻补角互补结合已知条件得到,再分当射线在上方时,当射线在下方时,两种情况根据垂线的定义得到,再根据角之间的关系进行求解即可.
【详解】解:∵,,
∴,
如图所示,当射线在上方时,
∵,
∴,
∴;
如图所示,当射线在下方时,
∵,
∴,
∴;
综上所述,度数为或.
故答案为:或.
14.4
【分析】本题考查点到直线的距离,此题关键是理解点A到BC的距离是从点A向BC作垂线,所得的垂线段.根据点到直线的距离即可判断.
【详解】解:∵,垂足为C.
∴点A到的距离,即.
故答案为:4
15./54度
【分析】本题考查了角的计算,由平角的定义和垂直的定义可得的度数.把握图中角之间的关系是解题的关键.
【详解】解: ,
,
,,
故答案为:.
16.或
【分析】本题主要考查了对顶角的定义和性质,掌握其性质是解本题的关键.
对顶角的定义:有一个公共顶点,且一个角的两条边分别是另一个角的两条边的反向延长线,那么这两个角就叫做对顶角.根据题意,利用对顶角的性质通过计算解出答案.
【详解】由题意,需讨论以下两种情况:
①如图1
∵,
∴ ;
∵与是对顶角;
∴,
∴.
②如图2
∵,
∴;
∵与是对顶角,
∴,
∴.
综上:或.
故答案为:或.
17.;
【分析】本题主要考查了平行线的判定与性质,过点C作是解答本题的关键,先由,求得,从而可知;过点C作,利用平行线的传递性可知,再根据平行线的性质,求出,,即可得出答案.
【详解】解:由题意可知,,,
,
,
,
,
过点C作,
,
,
,
.
18.(1)
(2)
(3)或
【分析】本题考查的是垂直的性质,角平分线的定义,以及对顶角和邻补角.
(1)根据,得,由,得到与互余,从而得出结果;
(2)根据,得到,由即可求解;
(3)先过点O作,再分两种情况根据角的和差关系可求的度数.
【详解】(1)解:,
,
,
,
;
(2)解:,
,
,
,
,
;
(3)解:如图,当在下方时,则,
由(2)知,
;
如图,当在上方时,则,
由(2)知,
,
故答案为:或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
