第一章 一元二次方程单元测试卷(含解析)
文档属性
| 名称 | 第一章 一元二次方程单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 726.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 05:58:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年 苏科版(2012)九年级上册 第一章 一元二次方程 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1. 是关于x的一元一次方程,则( )
A.0 B.1 C. D.或1
2.用配方法解方程时,配方后所得的方程为( )
A. B. C. D.
3.已知为关于的方程的三个实数根,则( )
A.3 B.4 C.5 D.6
4.电影《长津湖》上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达18亿元,将增长率记作x,则方程可以列为( )
A. B.
C. D.
5.小区有一块正方形的空地,后来从这块空地上划出部分区域进行绿化(如图),原空地一边减少了,另一边减少了,剩余空地的面积为,求原正方形空地的边长.设原正方形空地的边长为,则可列方程为( )
A.( B.
C. D.
6.已知是方程的一个根,则实数c的值是( )
A. B.0 C.1 D.2
7.若是一元二次方程的一个解,则的值为( )
A.0 B. C.2 D.
8.已知m,n是方程的两根,则( )
A.8 B.7 C.9 D.6
9.方程的一个实数根为m ,则的值是( )
A.2023 B.2021 C.2027 D.2029
10.如图,在矩形中,,,点从点出发沿以的速度向点移动,一直到达点为止;同时,点从点出发沿边以的速度向点移动. 设运动时间为,当时,( )
A. B.或4 C.或 D.
评卷人得分
二、填空题
11.已知有两个不相等的实数根,的取值范围是 .
12.已知是一元二次方程的两个实数根,则的值是 .
13.已知:关于x的方程①有两个符号不同的实数根,且;关于x的方程②有两个有理数根且两根之积等于2.求整数n的值 .
14.若一元二次方程的两个根为,,则的值为 .
15.已知关于的一元二次方程的一个根为2,则另一个根是 .
16.若,是方程的两根,则 .
评卷人得分
三、计算题
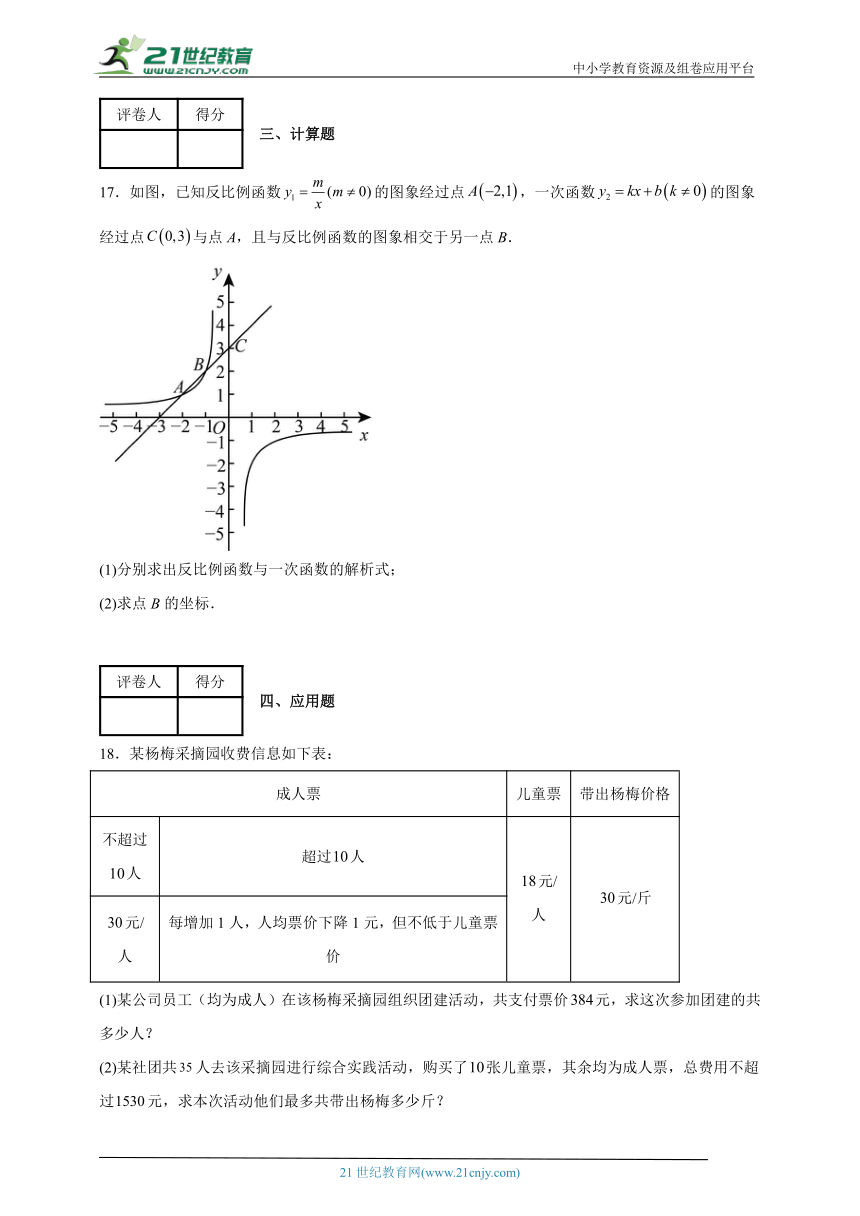
17.如图,已知反比例函数的图象经过点,一次函数的图象经过点与点A,且与反比例函数的图象相交于另一点B.
(1)分别求出反比例函数与一次函数的解析式;
(2)求点B的坐标.
评卷人得分
四、应用题
18.某杨梅采摘园收费信息如下表:
成人票 儿童票 带出杨梅价格
不超过人 超过人 元/人 元/斤
元/人 每增加1人,人均票价下降1元,但不低于儿童票价
(1)某公司员工(均为成人)在该杨梅采摘园组织团建活动,共支付票价元,求这次参加团建的共多少人?
(2)某社团共人去该采摘园进行综合实践活动,购买了张儿童票,其余均为成人票,总费用不超过元,求本次活动他们最多共带出杨梅多少斤?
参考答案:
1.C
【分析】本题主要考查一元一次方程的定义、绝对值,由是关于x的一元一次方程可得到关于a的一元一次不等式组,求解即可得到答案.
【详解】解:∵是关于x的一元一次方程,
∴,
解得:.
故选:C.
2.C
【分析】本题考查配方法解一元二次方程,利用配方法的求解过程解答即可.
【详解】解:移项,得,
配方,得,
则,
故选:C.
3.A
【分析】题目主要考查因式分解解一元二次方程及根与系数的关系,熟练掌握一元二次方程根与系数的关系是解题关键.
【详解】解:方程
即,
∴它的一个实数根为1,另外两个实数根之和为2,
∵
∴其中必有一根小于1,另一根大于1,
∴,,
∴
,
故选:A.
4.D
【分析】本题考查从实际问题中抽象出一元二次方程,解题的关键在于能够表示出第二玩耍和第三天的票房,设增长率为,则第二天的票房为,第三天的票房为,然后根据三天后累计票房收入达达18亿元列出方程即可.
【详解】解:设增长率为,则第二天的票房为,第三天的票房为,由题可得:
,
故选:D.
5.D
【分析】本题考查了由实际问题抽象出一元二次方程的知识,应熟记长方形的面积公式.另外求得剩余的空地的长和宽是解决本题的关键.
设原正方形的边长为,则剩余的空地长为,宽为.根据长方形的面积公式可列出方程.
【详解】解:设原正方形的边长为,依题意有
,
故选:D.
6.C
【分析】本题主要考查了方程的解的定义,掌握“使方程两边相等的未知数的值是方程的解”,是解题的关键.将代入得到关于c的方程,解之可得.
【详解】解:根据题意,将代入,得:
,
解得:,
故选:C.
7.B
【分析】本题考查了一元二次方程的解及解一元一次方程,将代入方程,建立关于m的一元一次方程,求解方程即可.
【详解】解:是一元二次方程的一个解,
,即,
解得:,
故选:B.
8.C
【分析】本题考查了根与系数的关系,若,是一元二次方程的两个根时,,熟记根与系数的关系是解题的关键.
先根据一元二次方程根与系数的关系得到, ,根据一元二次方程根的定义得到,然后利用整体代入的方法计算代数式的值即可.
【详解】解已知m,n是方程的两根,
,,,
,
,
=,
=,
=,
=
故选:C.
9.C
【分析】本题考查的是一元二次方程的解,求解代数式的值,本题由方程的解可得,再代入求值即可.
【详解】解:∵方程的一个实数根为m ,
∴,即,
∴,
故选C
10.C
【点评】此题考查了一元二次方程的运用.利用作垂线,构造直角三角形,运用勾股定理列方程是解题关键.
作,垂足为H,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
【详解】解:设P,Q两点从出发经过t秒时,点P,Q间的距离是,
作,垂足为H,
则,,.
,
可得:,
解得,.
答:P,Q两点从出发经过或秒时,点P,Q间的距离是.
故答案为:C.
11.且
【分析】本题主要考查根的判别式,由方程有两个不相等的实数根结合根的判别式即可得出关于的一元一次不等式,解之即可得出实数的取值范围,掌握方程根的情况与根的判别式的关系是解题的关键.
【详解】解:由题意得:,
∵有两个不相等的实数根,
∴且,
即且,
解得:且,
故答案为:且.
12./
【分析】本题考查了根与系数的关系:若,是一元二次方程的两根时,,.根据根与系数的关系得,,利用代数式变形分别得到,然后利用整体代入的方法计算.
【详解】因为是一元二次方程的两个实数根,
所以,
因为,
所以.
故答案为:
13.5或/或5
【分析】本题主要考查根与系数的关系、根的判别式、解二元一次方程组,根据①确定的取值范围,根据②利用根于系数的关系求出的值,根据方程有两个有理数根,得到,得到的二元一次方程组,求解即可.解题关键在于确定m的取值,然后分析出关于n和k的二元一次方程组.
【详解】解:∵有两个符号不同的实数根,且;
∴,
解得:;
∵的两根之积等于2,
∴,解得:或(舍去);
经检验:是原方程的解;
∴转化为:,
∵方程有两个有理数根,
∴,
∴,
∴,
∴或,
∴或;
故答案为:5或.
14.
【分析】本题考查了一元二次方程根与系数的关系;根据一元二次方程根与系数的关系可得,代入代数式,即可求解.
【详解】解:∵一元二次方程的两个根为,,
∴,
∴,
故答案为:.
15.
【分析】此题主要考查了根与系数的关系,掌握根与系数的关系式是解题关键.设方程的另一个根是,根据与系数的关系求出即可.
【详解】解:设方程的另一个根是,
根据根与系数的关系,得,
解得,
故答案为:.
16.
【分析】本题主要考查了一元二次方程解的定义,一元二次方程根与系数的关系,根据一元二次方程解的定义得到,根据根与系数的关系得到,再由进行代值求解即可.
【详解】解:∵,是方程的两根,
∴,
∴,
∴,
故答案为:.
17.(1),
(2)点B坐标为
【分析】本题考查反比例函数图象与一次函数图象的交点问题、解一元二次方程,解答关键是熟练掌握待定系数法求函数解析式的求解过程.
(1)利用待定系数法求解反比例函数与一次函数的解析式即可;
(2)联立两个函数解析式,求方程组的解即可求解.
【详解】(1)解:∵反比例函数的图象经过点,
∴,
∴反比例函数的解析式为;
∵一次函数的图象经过点与点A,
∴,解得,
∴一次函数的解析式为;
(2)解:联立方程组,解得或,
∴点B坐标为.
18.(1)
(2)
【分析】本题考查了一元二次方程的应用,一元一次不等式的应用.解题的关键在于根据题意正确的列等式、不等式.
(1)设这次参加团建的共人,由题意求得,依题意得,,计算求出满足要求的解即可;
(2)由题意求得,当成人人数大于或等于人时,成人票都是元/人, 由(人),,可得该社团购买的成人票为元/人,设本次活动他们最多共带出杨梅斤,依题意得,,计算求解,然后作答即可.
【详解】(1)解:设这次参加团建的共人,
由题意知,(元),(元),
∵,
∴,
依题意得,,整理得,,
,
∴或,
解得,或(舍去)
∴这次参加团建的共人;
(2)解:∵(人),(人),
∴当成人人数大于或等于人时,成人票都是元/人,
∵(人),,
∴该社团购买的成人票为元/人,
设本次活动他们最多共带出杨梅斤,
依题意得,,
解得,,
∴本次活动他们最多共带出杨梅斤.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年 苏科版(2012)九年级上册 第一章 一元二次方程 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1. 是关于x的一元一次方程,则( )
A.0 B.1 C. D.或1
2.用配方法解方程时,配方后所得的方程为( )
A. B. C. D.
3.已知为关于的方程的三个实数根,则( )
A.3 B.4 C.5 D.6
4.电影《长津湖》上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达18亿元,将增长率记作x,则方程可以列为( )
A. B.
C. D.
5.小区有一块正方形的空地,后来从这块空地上划出部分区域进行绿化(如图),原空地一边减少了,另一边减少了,剩余空地的面积为,求原正方形空地的边长.设原正方形空地的边长为,则可列方程为( )
A.( B.
C. D.
6.已知是方程的一个根,则实数c的值是( )
A. B.0 C.1 D.2
7.若是一元二次方程的一个解,则的值为( )
A.0 B. C.2 D.
8.已知m,n是方程的两根,则( )
A.8 B.7 C.9 D.6
9.方程的一个实数根为m ,则的值是( )
A.2023 B.2021 C.2027 D.2029
10.如图,在矩形中,,,点从点出发沿以的速度向点移动,一直到达点为止;同时,点从点出发沿边以的速度向点移动. 设运动时间为,当时,( )
A. B.或4 C.或 D.
评卷人得分
二、填空题
11.已知有两个不相等的实数根,的取值范围是 .
12.已知是一元二次方程的两个实数根,则的值是 .
13.已知:关于x的方程①有两个符号不同的实数根,且;关于x的方程②有两个有理数根且两根之积等于2.求整数n的值 .
14.若一元二次方程的两个根为,,则的值为 .
15.已知关于的一元二次方程的一个根为2,则另一个根是 .
16.若,是方程的两根,则 .
评卷人得分
三、计算题
17.如图,已知反比例函数的图象经过点,一次函数的图象经过点与点A,且与反比例函数的图象相交于另一点B.
(1)分别求出反比例函数与一次函数的解析式;
(2)求点B的坐标.
评卷人得分
四、应用题
18.某杨梅采摘园收费信息如下表:
成人票 儿童票 带出杨梅价格
不超过人 超过人 元/人 元/斤
元/人 每增加1人,人均票价下降1元,但不低于儿童票价
(1)某公司员工(均为成人)在该杨梅采摘园组织团建活动,共支付票价元,求这次参加团建的共多少人?
(2)某社团共人去该采摘园进行综合实践活动,购买了张儿童票,其余均为成人票,总费用不超过元,求本次活动他们最多共带出杨梅多少斤?
参考答案:
1.C
【分析】本题主要考查一元一次方程的定义、绝对值,由是关于x的一元一次方程可得到关于a的一元一次不等式组,求解即可得到答案.
【详解】解:∵是关于x的一元一次方程,
∴,
解得:.
故选:C.
2.C
【分析】本题考查配方法解一元二次方程,利用配方法的求解过程解答即可.
【详解】解:移项,得,
配方,得,
则,
故选:C.
3.A
【分析】题目主要考查因式分解解一元二次方程及根与系数的关系,熟练掌握一元二次方程根与系数的关系是解题关键.
【详解】解:方程
即,
∴它的一个实数根为1,另外两个实数根之和为2,
∵
∴其中必有一根小于1,另一根大于1,
∴,,
∴
,
故选:A.
4.D
【分析】本题考查从实际问题中抽象出一元二次方程,解题的关键在于能够表示出第二玩耍和第三天的票房,设增长率为,则第二天的票房为,第三天的票房为,然后根据三天后累计票房收入达达18亿元列出方程即可.
【详解】解:设增长率为,则第二天的票房为,第三天的票房为,由题可得:
,
故选:D.
5.D
【分析】本题考查了由实际问题抽象出一元二次方程的知识,应熟记长方形的面积公式.另外求得剩余的空地的长和宽是解决本题的关键.
设原正方形的边长为,则剩余的空地长为,宽为.根据长方形的面积公式可列出方程.
【详解】解:设原正方形的边长为,依题意有
,
故选:D.
6.C
【分析】本题主要考查了方程的解的定义,掌握“使方程两边相等的未知数的值是方程的解”,是解题的关键.将代入得到关于c的方程,解之可得.
【详解】解:根据题意,将代入,得:
,
解得:,
故选:C.
7.B
【分析】本题考查了一元二次方程的解及解一元一次方程,将代入方程,建立关于m的一元一次方程,求解方程即可.
【详解】解:是一元二次方程的一个解,
,即,
解得:,
故选:B.
8.C
【分析】本题考查了根与系数的关系,若,是一元二次方程的两个根时,,熟记根与系数的关系是解题的关键.
先根据一元二次方程根与系数的关系得到, ,根据一元二次方程根的定义得到,然后利用整体代入的方法计算代数式的值即可.
【详解】解已知m,n是方程的两根,
,,,
,
,
=,
=,
=,
=
故选:C.
9.C
【分析】本题考查的是一元二次方程的解,求解代数式的值,本题由方程的解可得,再代入求值即可.
【详解】解:∵方程的一个实数根为m ,
∴,即,
∴,
故选C
10.C
【点评】此题考查了一元二次方程的运用.利用作垂线,构造直角三角形,运用勾股定理列方程是解题关键.
作,垂足为H,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
【详解】解:设P,Q两点从出发经过t秒时,点P,Q间的距离是,
作,垂足为H,
则,,.
,
可得:,
解得,.
答:P,Q两点从出发经过或秒时,点P,Q间的距离是.
故答案为:C.
11.且
【分析】本题主要考查根的判别式,由方程有两个不相等的实数根结合根的判别式即可得出关于的一元一次不等式,解之即可得出实数的取值范围,掌握方程根的情况与根的判别式的关系是解题的关键.
【详解】解:由题意得:,
∵有两个不相等的实数根,
∴且,
即且,
解得:且,
故答案为:且.
12./
【分析】本题考查了根与系数的关系:若,是一元二次方程的两根时,,.根据根与系数的关系得,,利用代数式变形分别得到,然后利用整体代入的方法计算.
【详解】因为是一元二次方程的两个实数根,
所以,
因为,
所以.
故答案为:
13.5或/或5
【分析】本题主要考查根与系数的关系、根的判别式、解二元一次方程组,根据①确定的取值范围,根据②利用根于系数的关系求出的值,根据方程有两个有理数根,得到,得到的二元一次方程组,求解即可.解题关键在于确定m的取值,然后分析出关于n和k的二元一次方程组.
【详解】解:∵有两个符号不同的实数根,且;
∴,
解得:;
∵的两根之积等于2,
∴,解得:或(舍去);
经检验:是原方程的解;
∴转化为:,
∵方程有两个有理数根,
∴,
∴,
∴,
∴或,
∴或;
故答案为:5或.
14.
【分析】本题考查了一元二次方程根与系数的关系;根据一元二次方程根与系数的关系可得,代入代数式,即可求解.
【详解】解:∵一元二次方程的两个根为,,
∴,
∴,
故答案为:.
15.
【分析】此题主要考查了根与系数的关系,掌握根与系数的关系式是解题关键.设方程的另一个根是,根据与系数的关系求出即可.
【详解】解:设方程的另一个根是,
根据根与系数的关系,得,
解得,
故答案为:.
16.
【分析】本题主要考查了一元二次方程解的定义,一元二次方程根与系数的关系,根据一元二次方程解的定义得到,根据根与系数的关系得到,再由进行代值求解即可.
【详解】解:∵,是方程的两根,
∴,
∴,
∴,
故答案为:.
17.(1),
(2)点B坐标为
【分析】本题考查反比例函数图象与一次函数图象的交点问题、解一元二次方程,解答关键是熟练掌握待定系数法求函数解析式的求解过程.
(1)利用待定系数法求解反比例函数与一次函数的解析式即可;
(2)联立两个函数解析式,求方程组的解即可求解.
【详解】(1)解:∵反比例函数的图象经过点,
∴,
∴反比例函数的解析式为;
∵一次函数的图象经过点与点A,
∴,解得,
∴一次函数的解析式为;
(2)解:联立方程组,解得或,
∴点B坐标为.
18.(1)
(2)
【分析】本题考查了一元二次方程的应用,一元一次不等式的应用.解题的关键在于根据题意正确的列等式、不等式.
(1)设这次参加团建的共人,由题意求得,依题意得,,计算求出满足要求的解即可;
(2)由题意求得,当成人人数大于或等于人时,成人票都是元/人, 由(人),,可得该社团购买的成人票为元/人,设本次活动他们最多共带出杨梅斤,依题意得,,计算求解,然后作答即可.
【详解】(1)解:设这次参加团建的共人,
由题意知,(元),(元),
∵,
∴,
依题意得,,整理得,,
,
∴或,
解得,或(舍去)
∴这次参加团建的共人;
(2)解:∵(人),(人),
∴当成人人数大于或等于人时,成人票都是元/人,
∵(人),,
∴该社团购买的成人票为元/人,
设本次活动他们最多共带出杨梅斤,
依题意得,,
解得,,
∴本次活动他们最多共带出杨梅斤.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
