2023-2024学年北师大版数学九年级下册第二章二次函数单元检测试题(无答案)
文档属性
| 名称 | 2023-2024学年北师大版数学九年级下册第二章二次函数单元检测试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 506.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 00:00:00 | ||
图片预览


文档简介
二次函数单元检测试题
一、选择题(每题3分,共30分)
1.二次函数的顶点坐标是( )
A. B. C. D.
2.在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为( )
A. B. C. D.
3.已知,二次数的图象如图所示,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.将抛物线通过平移后,得到抛物线的解析式为,则平移的方向和距离是( )
A.向右平移2个单位长度,再向上平移3个单位长度
B.向右平移2个单位长度,再向下平移3个单位长度
C.向左平移2个单位长度,再向上平移3个单位长度
D.向左平移2个单位长度,再向下平移3个单位长度
5.二次函数的图象如图所示,则一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知抛物线,则当时,函数的最大值为( )
A. B. C.0 D.2
7.如图,抛物线经过正方形的三个顶点A,B,C,点B在轴上,则的值为( )
A. B. C. D.
8.如图,在菱形中,,,动点,同时从点出发,点以每秒个单位长度沿折线向终点运动;点以每秒个单位长度沿线段向终点运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为秒,的面积为个平方单位,则下列正确表示与函数关系的图象是( )
A. B. C. D.
9.如图,抛物线与x轴交于点,其中,下列四个结论:①;②;③;④不等式的解集为.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.已知,若关于x的方程的解为.关于x的方程的解为.则下列结论正确的是( )
A.B. C. D.
二、填空题(每题4分,共24分)
11.如图,抛物线与直线的两个交点坐标分别为,,则关于x的方程的解为 .
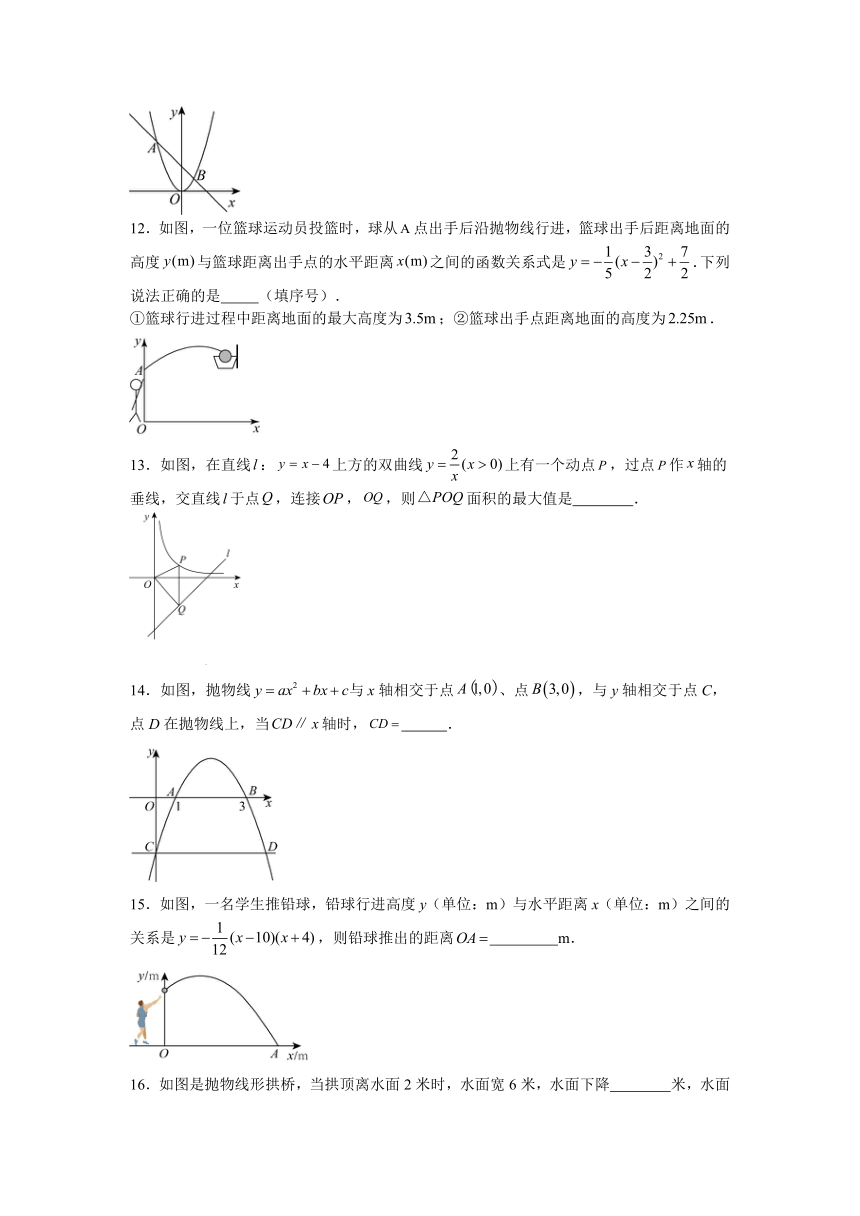
12.如图,一位篮球运动员投篮时,球从点出手后沿抛物线行进,篮球出手后距离地面的高度与篮球距离出手点的水平距离之间的函数关系式是.下列说法正确的是 (填序号).
①篮球行进过程中距离地面的最大高度为;②篮球出手点距离地面的高度为.
13.如图,在直线:上方的双曲线上有一个动点,过点作轴的垂线,交直线于点,连接,,则面积的最大值是 .
14.如图,抛物线与x轴相交于点、点,与y轴相交于点C,点D在抛物线上,当轴时, .
15.如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是,则铅球推出的距离 m.
16.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降 米,水面宽8米.
三、解答题(共66分)
17.(6分)
已知抛物线经过点和.
(1)求b,c的值;
(2)当时,求y的值.
18.(8分)
已知二次函数.
(1)求此二次函数图象的顶点坐标;
(2)当时,求函数值的取值范围.
19.(8分)
一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离的长.
20.(9分)如图,在平面直角坐标系中,直线l与x轴交于点,与y轴交于点,抛物线经过点A,B,且对称轴是直线.
(1)求直线l的解析式;
(2)求抛物线的解析式;
(3)点P是直线l下方抛物线上的一动点,过点P作轴,垂足为C,交直线l于点D,过点P作,垂足为M.求的最大值及此时P点的坐标.
21.(9分)如图,已知抛物线与y轴交于点C,与x轴交于A、B两点(点A在点B左边).
(1)请直接写出A、B、C三点的坐标;
(2)点P是第一象限内抛物线上一点,求面积最大时点P的坐标;
(3)如图①,已知点M在抛物线上,点N在x轴上,且四边形为平行四边形,求M点的横坐标.
22.(9分)在平面直角坐标系中,已知抛物线与x轴交于点两点,与y轴交于点,点P是抛物线上的一个动点.
(1)求抛物线的表达式;
(2)当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;
(3)过点P作x轴的垂线交直线于点M,连接,将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.
23.(8分)阅读下面方框内的内容,并完成相应的任务.
小丽学习了方程、不等式、函数后提出如下问题:如何求不等式的解集? 通过思考,小丽得到以下3种方法: 方法1 方程的两根为,,可得函数的图像与x轴的两个交点横坐标为、,画出函数图像,观察该图像在x轴下方的点,其横坐标的范围是不等式的解集. 方法2 不等式可变形为,问题转化为研究函数与的图像关系.画出函数图像,观察发现:两图像的交点横坐标也是、3;的图像在的图像下方的点,其横坐标的范围是该不等式的解集. 方法3 当时,不等式一定成立;当时,不等式变为;当时,不等式变为.问题转化为研究函数与的图像关系…
任务:
(1)不等式的解集为_____________;
(2)3种方法都运用了___________的数学思想方法(从下面选项中选1个序号即可);
A.分类讨论 B.转化思想 C.特殊到一般 D.数形结合
(3)请你根据方法3的思路,画出函数图像的简图,并结合图像作出解答.
24.(9分)某品牌大米远近闻名,深受广大消费者喜爱,某超市每天购进一批成本价为每千克4元的该大米,以不低于成本价且不超过每千克7元的价格销售.当每千克售价为5元时,每天售出大米;当每千克售价为6元时,每天售出大米,通过分析销售数据发现:每天销售大米的数量与每千克售价(元)满足一次函数关系.
(1)请直接写出y与x的函数关系式;
(2)超市将该大米每千克售价定为多少元时,每天销售该大米的利润可达到1800元?
(3)当每千克售价定为多少元时,每天获利最大?最大利润为多少?
答案第1页,共2页
一、选择题(每题3分,共30分)
1.二次函数的顶点坐标是( )
A. B. C. D.
2.在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为( )
A. B. C. D.
3.已知,二次数的图象如图所示,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.将抛物线通过平移后,得到抛物线的解析式为,则平移的方向和距离是( )
A.向右平移2个单位长度,再向上平移3个单位长度
B.向右平移2个单位长度,再向下平移3个单位长度
C.向左平移2个单位长度,再向上平移3个单位长度
D.向左平移2个单位长度,再向下平移3个单位长度
5.二次函数的图象如图所示,则一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知抛物线,则当时,函数的最大值为( )
A. B. C.0 D.2
7.如图,抛物线经过正方形的三个顶点A,B,C,点B在轴上,则的值为( )
A. B. C. D.
8.如图,在菱形中,,,动点,同时从点出发,点以每秒个单位长度沿折线向终点运动;点以每秒个单位长度沿线段向终点运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为秒,的面积为个平方单位,则下列正确表示与函数关系的图象是( )
A. B. C. D.
9.如图,抛物线与x轴交于点,其中,下列四个结论:①;②;③;④不等式的解集为.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.已知,若关于x的方程的解为.关于x的方程的解为.则下列结论正确的是( )
A.B. C. D.
二、填空题(每题4分,共24分)
11.如图,抛物线与直线的两个交点坐标分别为,,则关于x的方程的解为 .
12.如图,一位篮球运动员投篮时,球从点出手后沿抛物线行进,篮球出手后距离地面的高度与篮球距离出手点的水平距离之间的函数关系式是.下列说法正确的是 (填序号).
①篮球行进过程中距离地面的最大高度为;②篮球出手点距离地面的高度为.
13.如图,在直线:上方的双曲线上有一个动点,过点作轴的垂线,交直线于点,连接,,则面积的最大值是 .
14.如图,抛物线与x轴相交于点、点,与y轴相交于点C,点D在抛物线上,当轴时, .
15.如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是,则铅球推出的距离 m.
16.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降 米,水面宽8米.
三、解答题(共66分)
17.(6分)
已知抛物线经过点和.
(1)求b,c的值;
(2)当时,求y的值.
18.(8分)
已知二次函数.
(1)求此二次函数图象的顶点坐标;
(2)当时,求函数值的取值范围.
19.(8分)
一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离的长.
20.(9分)如图,在平面直角坐标系中,直线l与x轴交于点,与y轴交于点,抛物线经过点A,B,且对称轴是直线.
(1)求直线l的解析式;
(2)求抛物线的解析式;
(3)点P是直线l下方抛物线上的一动点,过点P作轴,垂足为C,交直线l于点D,过点P作,垂足为M.求的最大值及此时P点的坐标.
21.(9分)如图,已知抛物线与y轴交于点C,与x轴交于A、B两点(点A在点B左边).
(1)请直接写出A、B、C三点的坐标;
(2)点P是第一象限内抛物线上一点,求面积最大时点P的坐标;
(3)如图①,已知点M在抛物线上,点N在x轴上,且四边形为平行四边形,求M点的横坐标.
22.(9分)在平面直角坐标系中,已知抛物线与x轴交于点两点,与y轴交于点,点P是抛物线上的一个动点.
(1)求抛物线的表达式;
(2)当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;
(3)过点P作x轴的垂线交直线于点M,连接,将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.
23.(8分)阅读下面方框内的内容,并完成相应的任务.
小丽学习了方程、不等式、函数后提出如下问题:如何求不等式的解集? 通过思考,小丽得到以下3种方法: 方法1 方程的两根为,,可得函数的图像与x轴的两个交点横坐标为、,画出函数图像,观察该图像在x轴下方的点,其横坐标的范围是不等式的解集. 方法2 不等式可变形为,问题转化为研究函数与的图像关系.画出函数图像,观察发现:两图像的交点横坐标也是、3;的图像在的图像下方的点,其横坐标的范围是该不等式的解集. 方法3 当时,不等式一定成立;当时,不等式变为;当时,不等式变为.问题转化为研究函数与的图像关系…
任务:
(1)不等式的解集为_____________;
(2)3种方法都运用了___________的数学思想方法(从下面选项中选1个序号即可);
A.分类讨论 B.转化思想 C.特殊到一般 D.数形结合
(3)请你根据方法3的思路,画出函数图像的简图,并结合图像作出解答.
24.(9分)某品牌大米远近闻名,深受广大消费者喜爱,某超市每天购进一批成本价为每千克4元的该大米,以不低于成本价且不超过每千克7元的价格销售.当每千克售价为5元时,每天售出大米;当每千克售价为6元时,每天售出大米,通过分析销售数据发现:每天销售大米的数量与每千克售价(元)满足一次函数关系.
(1)请直接写出y与x的函数关系式;
(2)超市将该大米每千克售价定为多少元时,每天销售该大米的利润可达到1800元?
(3)当每千克售价定为多少元时,每天获利最大?最大利润为多少?
答案第1页,共2页
