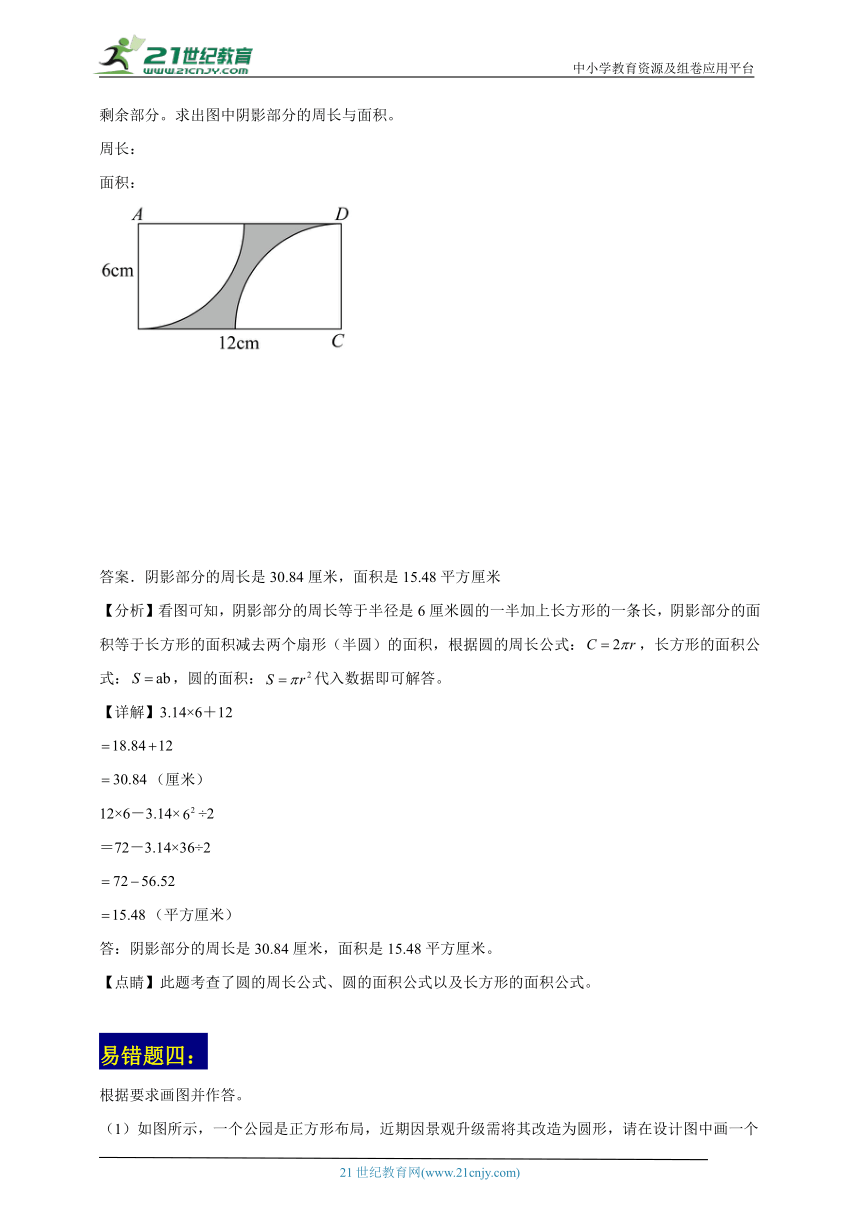
圆常考易错精选题-数学六年级上册人教版(含解析)
文档属性
| 名称 | 圆常考易错精选题-数学六年级上册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 16:22:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
圆常考易错精选题-数学六年级上册人教版
易错题一:
兰兰用3米长的绳子测量一棵树干横截面的周长,将绳子在树干上绕了3周还余17.4厘米,这棵树干的横截面的面积是多少平方厘米?
答案.706.5平方厘米
【分析】先用绳子的长减去17.4厘米,再除以3求出树干横截面的周长;由圆的周长可推导出,据此根据圆的周长求出圆的半径;最后利用圆的面积求出这棵树干的横截面的面积。
【详解】3米=300厘米
(300-17.4)÷3
=282.6÷3
=94.2(厘米)
94.2÷3.14÷2
=30÷2
=15(厘米)
3.14×152
=3.14×225
=706.5(平方厘米)
答:这棵树干的横截面的面积是706.5平方厘米。
【点睛】此题考查了圆的周长、圆的面积计算公式。在计算圆的面积时,不要把当成计算,应是。
易错题二:
下图是一面我国唐代外圆内方的铜镜。铜镜的直径是24cm。外面的圆与内部的正方形之间的面积是多少?
答案.164.16平方厘米
【分析】外面的圆与内部的正方形之间的面积=圆的面积-正方形的面积=圆的面积-三角形的面积×2,据此解答。
【详解】
=164.16(平方厘米)
答:外面的圆与内部的正方形之间的面积是164.16平方厘米。
【点睛】掌握圆的面积计算公式的应用是解答题目的关键。
易错题三:
请用圆规在图中长方形内,分别以、为圆心作圆心角是的最大扇形,并用阴影表示长方形的剩余部分。求出图中阴影部分的周长与面积。
周长:
面积:
答案.阴影部分的周长是30.84厘米,面积是15.48平方厘米
【分析】看图可知,阴影部分的周长等于半径是6厘米圆的一半加上长方形的一条长,阴影部分的面积等于长方形的面积减去两个扇形(半圆)的面积,根据圆的周长公式:,长方形的面积公式:,圆的面积:代入数据即可解答。
【详解】3.14×6+12
(厘米)
12×6-3.14×÷2
=72-3.14×36÷2
(平方厘米)
答:阴影部分的周长是30.84厘米,面积是15.48平方厘米。
【点睛】此题考查了圆的周长公式、圆的面积公式以及长方形的面积公式。
易错题四:
根据要求画图并作答。
(1)如图所示,一个公园是正方形布局,近期因景观升级需将其改造为圆形,请在设计图中画一个最小的圆,使它恰好能够围住正方形。(先用虚线表示出你是怎样找到圆心的,并给圆心标上字母O,再用实线画圆。)
(2)公园的南门到北门距离200米,扩建后公园面积增加多少平方米?
(3)小明现在的位置在公园的中心,他计划从东门离开搭乘地铁回家。地铁站在公园东门北偏东30°距离100米的位置,请画出小明前往地铁站的路线图。
答案.(1)见详解
(2)11400平方米
(3)见详解
【分析】(1)画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。据此先用虚线画出正方形对角线,对角线的交点是圆心,半径=对角线的一半,据此画出圆。
(2)增加的面积=圆的面积-正方形面积,南门到北门距离是圆的直径,圆的面积=圆周率×半径的平方,正方形可以看成两个三角形,三角形面积=底×高÷2,据此求出增加的面积。
(3)用方向和距离结合来画路线时,要注意三个要素:一是观测点(即参照物),二是方向,三是距离。看图可知,图上1段表示50米,实际距离÷50=要画的段数。
【详解】(1)如下图:
(3)100÷50=2(段),如下图:
(2)200÷2=100(米)
3.14×1002-200×100÷2×2
=3.14×10000-20000
=31400-20000
=11400(平方米)
答:扩建后公园面积增加11400平方米。
【点睛】关键是掌握画圆的方法,能根据方向、角度和距离画出路线图。
精选题练习
一、选择题
1.A、B两只小蚂蚁从甲到乙分别走两条路,比较这两条路线( )。
A.蚂蚁A走的长 B.蚂蚁B走的长 C.一样长 D.无法确定
2.下图的周长是( )。
A.(π+1)d B.πd+d
C.d D.πd
3.半圆的周长是20.56cm的圆,则直径的长度是( )。
A.4cm B.6cm C.8cm D.10cm
4.如图,图形(单位:分米)涂色部分的面积是( )。
A.12.84dm B.9.24dm C.18.24dm D.9.42dm
5.在图中画一个最大的正方形,如图所示,已知阴影部分的面积为a平方厘米,则圆的面积是( )平方厘米.
A.2aπ B.πa C.4a+π D.4a+
6.小圆半径是大圆半径的,小圆的面积是大圆面积的( )。
A. B. C. D.
二、填空题
7.用圆规和直尺画一个半圆,圆规两脚张开3cm,这个半圆的周长是( )cm,面积是( )cm2。
8.一个圆形水池的直径是6m,在这个水池的周围修一条宽1m的小路,这条小路的面积是( )m2。为了安全,在水池的一周围上栏杆,栏杆长( )m。
9.在一个正方形里画一个最大的圆,这个圆的周长是这个正方形周长的( ),这个圆的面积是正方形面积的( ).
10.在一块长130厘米,宽118厘米的长方形钢板上,最多能截取( )个半径是2分米的圆形钢板。
11.如图,圆的面积是12.56平方厘米,正方形的面积是( )平方厘米。
12.一个圆的半径和直径的比是( );如果两个圆的直径的比是2∶3,那么它们的面积比是( )。
13.用一张周长为24dm的正方形纸,剪一个最大的圆,它的面积是( ).
14.如图,把一个圆平均分成若干份,拼成一个近似的平行四边形,这个平行四边形的周长比圆的周长多8cm,这个圆的面积是( )cm2。
三、图形计算
15.计算图中阴影部分的面积。(单位:厘米)
16.计算下图中阴影部分的面积。
四、解答题
17.用一根长30分米的绳子绕一根圆柱形柱子三圈后还多1.74分米,这根圆柱形柱子的直径是多少分米?
18.如图,李奶奶用竹篱笆靠墙围成一个半径为5米的半圆形养鸡场,篱笆长多少米?
19.王老师家到学校的路程是3500米,他8:10时骑自行车从家到学校去,这辆自行车车轮外直径是60厘米,平均每分钟转100周。如果学校8:30上班,请问王老师能不能按时到校?为什么?
20.一个圆环,内圆的周长是31.4厘米,外圆的周长是62.8厘米,圆环的宽是多少厘米?
21.大本钟——伦敦市的标志性建筑物,钟盘上时针的长度是2.75m。
(1)大本钟的时针经过8小时,时针的尖端走过的路程是多少米?(得数保留两位小数)
(2)如果这个时钟的时针尖端走过的路程是8.635m,则时针走过了多少小时?
22.如下图,一个圆形环岛的直径是60m,中间是一个直径是20m的圆形花坛,其他地方是草坪。如果每平方米草皮8元,铺满这个环形草坪买草皮需要多少钱?(π取3.14)
参考答案:
1.C
【分析】假设大圆直径是D,三个小圆直径分别是d1,d2,d3,根据圆的周长公式,计算出大圆周长的一半,三个小圆周长一半的和,进行比较即可。
【详解】假设大圆直径是D,三个小圆直径分别是d1,d2,d3,D= d1+d2+d3,
大圆周长的一半=πD÷2
三个小圆周长一半的和:πd1÷2+πd2÷2+πd3÷2=π(d1+d2+d3)÷2=πD÷2
两条路线一样长。
故答案为:C
【点睛】关键是熟悉圆的周长公式,圆的周长=πd。
2.A
【解析】略
3.C
【分析】把半圆的直径设为未知数,半圆的周长比圆周长的一半多一条直径的长度,根据“”表示出圆周长的一半,等量关系式:圆周长的一半+直径=半圆的周长,据此解答。
【详解】解:设直径的长度是dcm。
3.14d÷2+d=20.56
1.57d+d=20.56
2.57d=20.56
d=20.56÷2.57
d=8
所以,直径的长度是8cm。
故答案为:C
【点睛】掌握圆的周长计算公式,理解圆的一半的周长和半圆周长的区别是解答题目的关键。
4.C
【分析】根据图形可知,涂色部分的面积=圆的面积-两个三角形的面积,已知圆的直径是8dm,可求出圆的面积;三角形的底边长就是圆的直径,高就是圆的半径,据此解答即可。
【详解】圆的面积:3.14×(8÷2)2
=3.14×16
=50.24(平方分米)
两个三角形的面积:8×4÷2×2
=32÷2×2
=16×2
=32(平方分米)
涂色部分的面积:50.24-32=18.24(平方分米)
故选:C
【点睛】本题考查圆的面积和三角形的面积,熟记它们的面积公式是解题的关键。
5.A
【详解】试题分析:因为阴影部分是一个等腰直角三角形,两条直角边等于圆的半径,设出圆的半径,则阴影部分面积,=r×r÷2,即可计算出圆的半径的平方,代入圆的面积公式计算即可.
解:设圆的半径为r,则阴影部分面积为:
r2÷2=a,所以r2=2a(平方厘米),
圆的面积为:π×2a=2aπ(平方厘米).
故选A.
点评:解决本题的关键是明确阴影部分是一个等腰直角三角形,两条直角边等于圆的半径,求出圆的半径的平方.
6.C
【分析】假设大圆的半径是5,根据分数乘法的意义,求出小圆的半径等于4,再利用圆的面积公式:S=,分别求出大圆和小圆的面积,再用小圆的面积除以大圆的面积,即可求出小圆的面积是大圆面积的几分之几。
【详解】假设大圆的半径是5,
5×=4
3.14×42÷(3.14×52)
=3.14×16÷(3.14×25)
=3.14×16÷3.14÷25
=3.14÷3.14×(16÷25)
=1×
=
故答案为:C
【点睛】此题的解题关键是通过分数乘法的意义,利用圆的面积公式,根据求一个数占另一个数的几分之几的计算方法,求出结果。
7. 15.42 14.13
【分析】圆规两脚间的距离是圆的半径。圆周长C=2πr,圆面积S=πr2,将数据代入公式,求出半径是3cm圆的周长和面积。将圆的周长除以2,再加上直径,求出半圆的周长。将圆的面积除以2,求出半圆的面积。
【详解】2×3.14×3÷2+3×2
=9.42+6
=15.42(cm)
3.14×32÷2
=28.26÷2
=14.13(cm2)
所以,这个半圆的周长是15.42cm,面积是14.13cm2。
【点睛】本题考查了半圆的周长和面积,灵活运用圆的周长和面积公式是解题的关键。
8. 21.98 18.84
【分析】根据题意,在圆形水池的周围修一条宽1m小路,求这条小路的面积,就是求圆环的面积;根据圆环的面积公式S环=π(R2-r2),求出这条小路的面积;
在水池的一周围上栏杆,求栏杆的长度,就是求圆形水池的周长,根据圆的周长公式C=πd,代入数据计算即可。
【详解】6÷2=3(m)
3+1=4(m)
圆环的面积(小路的面积):
3.14×(42-32)
=3.14×(16-9)
=3.14×7
=21.98(m2)
圆的周长(栏杆的长度):
3.14×6=18.84(m)
这条小路的面积是21.98m2,栏杆长18.84m。
【点睛】本题考查圆环的面积、圆的周长公式的运用,找出圆环的内圆、外圆的半径是求圆环面积的关键。
9.
【详解】本题考查的是正方形与圆的相关知识.要求它们周长、面积之间的关系,应该分别将它们的周长、面积表示出来,再找关系.
在一个正方形里面画一个最大的圆,则这个圆的直径就是正方形的边长.我们不妨设正方形的边长为a,则圆的直径也是a,所以正方形的周长是4a,面积是a2;圆的周长是πa,面积是π=.故圆的周长是正方形周长的=;圆的面积是正方形面积的=.
10.6
【分析】先统一单位,2分米=20厘米,半径是20厘米的圆形钢板直径是40厘米,先分别计算出在长方形钢板的长和宽上,各能截取多少个40厘米,再将得到的值相乘,就是能截取的直径为40厘米的圆形钢板的个数。
【详解】2分米=20厘米
130÷40≈3(个)
118÷40≈2(个)
3×2=6(个)
【点睛】此题属于图形的切拼,要注意不能用总面积除以每个小圆形的面积。
11.4
【分析】观察图形可知,圆的半径相当于正方形的边长,根据圆的面积公式:S=πr2,据此可求出半径的平方是多少,因为正方形的面积=边长×边长即圆的半径的平方。据此解答即可。
【详解】12.56÷3.14=4(平方厘米)
【点睛】本题考查正方形和圆的面积,明确该图中圆的半径相当于正方形的边长是解题的关键。
12. 1∶2 4∶9
【分析】假设r为1,根据d=2r,则d为2,根据比的意义写出半径和直径的比即可;如果两个圆的直径的比是2∶3,则它们的半径比也是2∶3,根据S=πr2,则它们的面积比是(4π)∶(9π),再化简即可。
【详解】假设r为1,
1×2=2
一个圆的半径和直径的比是1∶2,
根据直径和半径的关系,如果两个圆的直径的比是2∶3,则它们的半径比也是2∶3,
(π×2×2)∶(π×3×3)
=(4π)∶(9π)
=(4π÷π)∶(9π÷π)
=4∶9
如果两个圆的直径的比是2∶3,那么它们的面积比是4∶9。
【点睛】本题考查了比的意义和化简,关键是掌握圆的半径、直径和面积之间的关系。
13.28.26dm2
【解析】略
14.50.24
【分析】把一个圆平均分成若干份,拼成一个近似的平行四边形,这个平行四边形的周长比圆的周长多两条半径的长度,即8cm,据此求出一条半径的长度,再根据圆的面积公式:S=πr2,据此计算即可。
【详解】8÷2=4(cm)
3.14×42
=3.14×16
=50.24(cm2)
则这个圆的面积是50.24cm2。
【点睛】本题考查圆的周长和面积,明确该平行四边形的周长比圆的周长多两条半径的长度是解题的关键。
15.0.86平方厘米
【分析】图中阴影部分的面积=正方形的面积-圆的面积,图中圆的直径相当于正方形的边长,根据正方形的面积=边长×边长,圆的面积公式:S=πr2,据此代入数值进行计算即可。
【详解】2×2-3.14×(2÷2)2
=4-3.14×1
=4-3.14
=0.86(平方厘米)
16.6.28cm2
【分析】
如图,把下面的阴影小半圆移补到空白小半圆处,这样阴影部分是一个直径为4cm的大半圆;根据圆的面积公式S=πr2,求出圆的面积,再除以2,即是阴影部分的面积。
【详解】3.14×(4÷2)2÷2
=3.14×4÷2
=12.56÷2
=6.28(cm2)
17.3分米
【分析】用这个绳子的长度减去剩余的1.74分米,求出这个柱子底面周长的3倍,再除以3求出柱子的底面周长,然后根据圆的周长公式:C=πd,那么d=C÷π,把数据代入公式解答。
【详解】(30-1.74)÷3÷3.14
=28.26÷3÷3.14
=9.42÷3.14
=3(分米)
答:这个柱子的直径是3分米。
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
18.15.7米
【分析】观察题意可知,篱笆的长度相当于半径是5米的圆周长的一半,根据圆周长公式:C=2πr,用2×3.14×5÷2即可求出篱笆长多少米。
【详解】2×3.14×5÷2
=31.4÷2
=15.7(米)
答:篱笆长15.7米。
【点睛】本题考查了圆周长公式的灵活应用。
19.能;车轮20分钟转动的圈数比从家到学校需要转动的圈数多
【分析】根据圆的周长公式,求出车轮转一周的距离,用路程÷转一周的距离=转的圈数,再求出20分钟转的圈数,比较即可。
【详解】8:30-8:10=20(分)
3500÷(3.14×0.6)
=3500÷1.884
≈1857.7(圈)
20×100=2000(圈)
1857.7<2000
答:王老师能按时到校,车轮20分钟转动的圈数比从家到学校需要转动的圈数多。
【点睛】关键是掌握圆的周长公式,圆的周长=πd,终点时间-起点时间=经过时间。
20.5cm
【详解】C内=2πr内=31.4
r内=31.4÷3.14÷2=5(cm)
C外=2πr外=62.8
r外=62.8÷3.14÷2=10(cm)
r外-r内=10-5=5(cm)
21.(1)11.51m
(2)6小时
【分析】(1)因为时针走一圈是12小时,当大本钟的时针经过8小时即是走了圆周长的,求走过的路程即是求以275米为半径的圆周长的即可;
(2)如果这个时钟的时针尖端走过的路程是8.635m,则时针走过了几小时,用走过的路程除以周长,结果即是时针走过的时间与12小时的分率,据此解答。
【详解】(1)3.14×2.75×2×
=8.635×2×
=17.27×
≈11.51(m)
答:时针的尖端走过的路程是11.51米。
(2)8.635÷(3.14×2.75×2)×12
=8.635÷17.27×12
=0.5×12
=6(小时)
答:时针走过了6小时。
【点睛】此题考查的是圆周长在实际生活中的应用,关键是把实际问题转化成数学问题进行解答。
22.20096元
【分析】根据题意,用圆形环岛的面积减去中间圆形花坛的面积就是草坪的占地面积,再用草坪的占地面积乘每平方米草皮的单价,即可求出铺满这个环形草坪买草皮需要的钱数。
【详解】60÷2=30(米)
20÷2=10(米)
3.14×(302-102)×8
=3.14×(900-100)×8
=3.14×800×8
=2512×8
=20096(元)
答:铺满这个环形草坪买草皮需要20096元钱。
【点睛】本题主要考查圆环的面积的计算方法,即大圆的面积减去小圆的面积。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆常考易错精选题-数学六年级上册人教版
易错题一:
兰兰用3米长的绳子测量一棵树干横截面的周长,将绳子在树干上绕了3周还余17.4厘米,这棵树干的横截面的面积是多少平方厘米?
答案.706.5平方厘米
【分析】先用绳子的长减去17.4厘米,再除以3求出树干横截面的周长;由圆的周长可推导出,据此根据圆的周长求出圆的半径;最后利用圆的面积求出这棵树干的横截面的面积。
【详解】3米=300厘米
(300-17.4)÷3
=282.6÷3
=94.2(厘米)
94.2÷3.14÷2
=30÷2
=15(厘米)
3.14×152
=3.14×225
=706.5(平方厘米)
答:这棵树干的横截面的面积是706.5平方厘米。
【点睛】此题考查了圆的周长、圆的面积计算公式。在计算圆的面积时,不要把当成计算,应是。
易错题二:
下图是一面我国唐代外圆内方的铜镜。铜镜的直径是24cm。外面的圆与内部的正方形之间的面积是多少?
答案.164.16平方厘米
【分析】外面的圆与内部的正方形之间的面积=圆的面积-正方形的面积=圆的面积-三角形的面积×2,据此解答。
【详解】
=164.16(平方厘米)
答:外面的圆与内部的正方形之间的面积是164.16平方厘米。
【点睛】掌握圆的面积计算公式的应用是解答题目的关键。
易错题三:
请用圆规在图中长方形内,分别以、为圆心作圆心角是的最大扇形,并用阴影表示长方形的剩余部分。求出图中阴影部分的周长与面积。
周长:
面积:
答案.阴影部分的周长是30.84厘米,面积是15.48平方厘米
【分析】看图可知,阴影部分的周长等于半径是6厘米圆的一半加上长方形的一条长,阴影部分的面积等于长方形的面积减去两个扇形(半圆)的面积,根据圆的周长公式:,长方形的面积公式:,圆的面积:代入数据即可解答。
【详解】3.14×6+12
(厘米)
12×6-3.14×÷2
=72-3.14×36÷2
(平方厘米)
答:阴影部分的周长是30.84厘米,面积是15.48平方厘米。
【点睛】此题考查了圆的周长公式、圆的面积公式以及长方形的面积公式。
易错题四:
根据要求画图并作答。
(1)如图所示,一个公园是正方形布局,近期因景观升级需将其改造为圆形,请在设计图中画一个最小的圆,使它恰好能够围住正方形。(先用虚线表示出你是怎样找到圆心的,并给圆心标上字母O,再用实线画圆。)
(2)公园的南门到北门距离200米,扩建后公园面积增加多少平方米?
(3)小明现在的位置在公园的中心,他计划从东门离开搭乘地铁回家。地铁站在公园东门北偏东30°距离100米的位置,请画出小明前往地铁站的路线图。
答案.(1)见详解
(2)11400平方米
(3)见详解
【分析】(1)画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。据此先用虚线画出正方形对角线,对角线的交点是圆心,半径=对角线的一半,据此画出圆。
(2)增加的面积=圆的面积-正方形面积,南门到北门距离是圆的直径,圆的面积=圆周率×半径的平方,正方形可以看成两个三角形,三角形面积=底×高÷2,据此求出增加的面积。
(3)用方向和距离结合来画路线时,要注意三个要素:一是观测点(即参照物),二是方向,三是距离。看图可知,图上1段表示50米,实际距离÷50=要画的段数。
【详解】(1)如下图:
(3)100÷50=2(段),如下图:
(2)200÷2=100(米)
3.14×1002-200×100÷2×2
=3.14×10000-20000
=31400-20000
=11400(平方米)
答:扩建后公园面积增加11400平方米。
【点睛】关键是掌握画圆的方法,能根据方向、角度和距离画出路线图。
精选题练习
一、选择题
1.A、B两只小蚂蚁从甲到乙分别走两条路,比较这两条路线( )。
A.蚂蚁A走的长 B.蚂蚁B走的长 C.一样长 D.无法确定
2.下图的周长是( )。
A.(π+1)d B.πd+d
C.d D.πd
3.半圆的周长是20.56cm的圆,则直径的长度是( )。
A.4cm B.6cm C.8cm D.10cm
4.如图,图形(单位:分米)涂色部分的面积是( )。
A.12.84dm B.9.24dm C.18.24dm D.9.42dm
5.在图中画一个最大的正方形,如图所示,已知阴影部分的面积为a平方厘米,则圆的面积是( )平方厘米.
A.2aπ B.πa C.4a+π D.4a+
6.小圆半径是大圆半径的,小圆的面积是大圆面积的( )。
A. B. C. D.
二、填空题
7.用圆规和直尺画一个半圆,圆规两脚张开3cm,这个半圆的周长是( )cm,面积是( )cm2。
8.一个圆形水池的直径是6m,在这个水池的周围修一条宽1m的小路,这条小路的面积是( )m2。为了安全,在水池的一周围上栏杆,栏杆长( )m。
9.在一个正方形里画一个最大的圆,这个圆的周长是这个正方形周长的( ),这个圆的面积是正方形面积的( ).
10.在一块长130厘米,宽118厘米的长方形钢板上,最多能截取( )个半径是2分米的圆形钢板。
11.如图,圆的面积是12.56平方厘米,正方形的面积是( )平方厘米。
12.一个圆的半径和直径的比是( );如果两个圆的直径的比是2∶3,那么它们的面积比是( )。
13.用一张周长为24dm的正方形纸,剪一个最大的圆,它的面积是( ).
14.如图,把一个圆平均分成若干份,拼成一个近似的平行四边形,这个平行四边形的周长比圆的周长多8cm,这个圆的面积是( )cm2。
三、图形计算
15.计算图中阴影部分的面积。(单位:厘米)
16.计算下图中阴影部分的面积。
四、解答题
17.用一根长30分米的绳子绕一根圆柱形柱子三圈后还多1.74分米,这根圆柱形柱子的直径是多少分米?
18.如图,李奶奶用竹篱笆靠墙围成一个半径为5米的半圆形养鸡场,篱笆长多少米?
19.王老师家到学校的路程是3500米,他8:10时骑自行车从家到学校去,这辆自行车车轮外直径是60厘米,平均每分钟转100周。如果学校8:30上班,请问王老师能不能按时到校?为什么?
20.一个圆环,内圆的周长是31.4厘米,外圆的周长是62.8厘米,圆环的宽是多少厘米?
21.大本钟——伦敦市的标志性建筑物,钟盘上时针的长度是2.75m。
(1)大本钟的时针经过8小时,时针的尖端走过的路程是多少米?(得数保留两位小数)
(2)如果这个时钟的时针尖端走过的路程是8.635m,则时针走过了多少小时?
22.如下图,一个圆形环岛的直径是60m,中间是一个直径是20m的圆形花坛,其他地方是草坪。如果每平方米草皮8元,铺满这个环形草坪买草皮需要多少钱?(π取3.14)
参考答案:
1.C
【分析】假设大圆直径是D,三个小圆直径分别是d1,d2,d3,根据圆的周长公式,计算出大圆周长的一半,三个小圆周长一半的和,进行比较即可。
【详解】假设大圆直径是D,三个小圆直径分别是d1,d2,d3,D= d1+d2+d3,
大圆周长的一半=πD÷2
三个小圆周长一半的和:πd1÷2+πd2÷2+πd3÷2=π(d1+d2+d3)÷2=πD÷2
两条路线一样长。
故答案为:C
【点睛】关键是熟悉圆的周长公式,圆的周长=πd。
2.A
【解析】略
3.C
【分析】把半圆的直径设为未知数,半圆的周长比圆周长的一半多一条直径的长度,根据“”表示出圆周长的一半,等量关系式:圆周长的一半+直径=半圆的周长,据此解答。
【详解】解:设直径的长度是dcm。
3.14d÷2+d=20.56
1.57d+d=20.56
2.57d=20.56
d=20.56÷2.57
d=8
所以,直径的长度是8cm。
故答案为:C
【点睛】掌握圆的周长计算公式,理解圆的一半的周长和半圆周长的区别是解答题目的关键。
4.C
【分析】根据图形可知,涂色部分的面积=圆的面积-两个三角形的面积,已知圆的直径是8dm,可求出圆的面积;三角形的底边长就是圆的直径,高就是圆的半径,据此解答即可。
【详解】圆的面积:3.14×(8÷2)2
=3.14×16
=50.24(平方分米)
两个三角形的面积:8×4÷2×2
=32÷2×2
=16×2
=32(平方分米)
涂色部分的面积:50.24-32=18.24(平方分米)
故选:C
【点睛】本题考查圆的面积和三角形的面积,熟记它们的面积公式是解题的关键。
5.A
【详解】试题分析:因为阴影部分是一个等腰直角三角形,两条直角边等于圆的半径,设出圆的半径,则阴影部分面积,=r×r÷2,即可计算出圆的半径的平方,代入圆的面积公式计算即可.
解:设圆的半径为r,则阴影部分面积为:
r2÷2=a,所以r2=2a(平方厘米),
圆的面积为:π×2a=2aπ(平方厘米).
故选A.
点评:解决本题的关键是明确阴影部分是一个等腰直角三角形,两条直角边等于圆的半径,求出圆的半径的平方.
6.C
【分析】假设大圆的半径是5,根据分数乘法的意义,求出小圆的半径等于4,再利用圆的面积公式:S=,分别求出大圆和小圆的面积,再用小圆的面积除以大圆的面积,即可求出小圆的面积是大圆面积的几分之几。
【详解】假设大圆的半径是5,
5×=4
3.14×42÷(3.14×52)
=3.14×16÷(3.14×25)
=3.14×16÷3.14÷25
=3.14÷3.14×(16÷25)
=1×
=
故答案为:C
【点睛】此题的解题关键是通过分数乘法的意义,利用圆的面积公式,根据求一个数占另一个数的几分之几的计算方法,求出结果。
7. 15.42 14.13
【分析】圆规两脚间的距离是圆的半径。圆周长C=2πr,圆面积S=πr2,将数据代入公式,求出半径是3cm圆的周长和面积。将圆的周长除以2,再加上直径,求出半圆的周长。将圆的面积除以2,求出半圆的面积。
【详解】2×3.14×3÷2+3×2
=9.42+6
=15.42(cm)
3.14×32÷2
=28.26÷2
=14.13(cm2)
所以,这个半圆的周长是15.42cm,面积是14.13cm2。
【点睛】本题考查了半圆的周长和面积,灵活运用圆的周长和面积公式是解题的关键。
8. 21.98 18.84
【分析】根据题意,在圆形水池的周围修一条宽1m小路,求这条小路的面积,就是求圆环的面积;根据圆环的面积公式S环=π(R2-r2),求出这条小路的面积;
在水池的一周围上栏杆,求栏杆的长度,就是求圆形水池的周长,根据圆的周长公式C=πd,代入数据计算即可。
【详解】6÷2=3(m)
3+1=4(m)
圆环的面积(小路的面积):
3.14×(42-32)
=3.14×(16-9)
=3.14×7
=21.98(m2)
圆的周长(栏杆的长度):
3.14×6=18.84(m)
这条小路的面积是21.98m2,栏杆长18.84m。
【点睛】本题考查圆环的面积、圆的周长公式的运用,找出圆环的内圆、外圆的半径是求圆环面积的关键。
9.
【详解】本题考查的是正方形与圆的相关知识.要求它们周长、面积之间的关系,应该分别将它们的周长、面积表示出来,再找关系.
在一个正方形里面画一个最大的圆,则这个圆的直径就是正方形的边长.我们不妨设正方形的边长为a,则圆的直径也是a,所以正方形的周长是4a,面积是a2;圆的周长是πa,面积是π=.故圆的周长是正方形周长的=;圆的面积是正方形面积的=.
10.6
【分析】先统一单位,2分米=20厘米,半径是20厘米的圆形钢板直径是40厘米,先分别计算出在长方形钢板的长和宽上,各能截取多少个40厘米,再将得到的值相乘,就是能截取的直径为40厘米的圆形钢板的个数。
【详解】2分米=20厘米
130÷40≈3(个)
118÷40≈2(个)
3×2=6(个)
【点睛】此题属于图形的切拼,要注意不能用总面积除以每个小圆形的面积。
11.4
【分析】观察图形可知,圆的半径相当于正方形的边长,根据圆的面积公式:S=πr2,据此可求出半径的平方是多少,因为正方形的面积=边长×边长即圆的半径的平方。据此解答即可。
【详解】12.56÷3.14=4(平方厘米)
【点睛】本题考查正方形和圆的面积,明确该图中圆的半径相当于正方形的边长是解题的关键。
12. 1∶2 4∶9
【分析】假设r为1,根据d=2r,则d为2,根据比的意义写出半径和直径的比即可;如果两个圆的直径的比是2∶3,则它们的半径比也是2∶3,根据S=πr2,则它们的面积比是(4π)∶(9π),再化简即可。
【详解】假设r为1,
1×2=2
一个圆的半径和直径的比是1∶2,
根据直径和半径的关系,如果两个圆的直径的比是2∶3,则它们的半径比也是2∶3,
(π×2×2)∶(π×3×3)
=(4π)∶(9π)
=(4π÷π)∶(9π÷π)
=4∶9
如果两个圆的直径的比是2∶3,那么它们的面积比是4∶9。
【点睛】本题考查了比的意义和化简,关键是掌握圆的半径、直径和面积之间的关系。
13.28.26dm2
【解析】略
14.50.24
【分析】把一个圆平均分成若干份,拼成一个近似的平行四边形,这个平行四边形的周长比圆的周长多两条半径的长度,即8cm,据此求出一条半径的长度,再根据圆的面积公式:S=πr2,据此计算即可。
【详解】8÷2=4(cm)
3.14×42
=3.14×16
=50.24(cm2)
则这个圆的面积是50.24cm2。
【点睛】本题考查圆的周长和面积,明确该平行四边形的周长比圆的周长多两条半径的长度是解题的关键。
15.0.86平方厘米
【分析】图中阴影部分的面积=正方形的面积-圆的面积,图中圆的直径相当于正方形的边长,根据正方形的面积=边长×边长,圆的面积公式:S=πr2,据此代入数值进行计算即可。
【详解】2×2-3.14×(2÷2)2
=4-3.14×1
=4-3.14
=0.86(平方厘米)
16.6.28cm2
【分析】
如图,把下面的阴影小半圆移补到空白小半圆处,这样阴影部分是一个直径为4cm的大半圆;根据圆的面积公式S=πr2,求出圆的面积,再除以2,即是阴影部分的面积。
【详解】3.14×(4÷2)2÷2
=3.14×4÷2
=12.56÷2
=6.28(cm2)
17.3分米
【分析】用这个绳子的长度减去剩余的1.74分米,求出这个柱子底面周长的3倍,再除以3求出柱子的底面周长,然后根据圆的周长公式:C=πd,那么d=C÷π,把数据代入公式解答。
【详解】(30-1.74)÷3÷3.14
=28.26÷3÷3.14
=9.42÷3.14
=3(分米)
答:这个柱子的直径是3分米。
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
18.15.7米
【分析】观察题意可知,篱笆的长度相当于半径是5米的圆周长的一半,根据圆周长公式:C=2πr,用2×3.14×5÷2即可求出篱笆长多少米。
【详解】2×3.14×5÷2
=31.4÷2
=15.7(米)
答:篱笆长15.7米。
【点睛】本题考查了圆周长公式的灵活应用。
19.能;车轮20分钟转动的圈数比从家到学校需要转动的圈数多
【分析】根据圆的周长公式,求出车轮转一周的距离,用路程÷转一周的距离=转的圈数,再求出20分钟转的圈数,比较即可。
【详解】8:30-8:10=20(分)
3500÷(3.14×0.6)
=3500÷1.884
≈1857.7(圈)
20×100=2000(圈)
1857.7<2000
答:王老师能按时到校,车轮20分钟转动的圈数比从家到学校需要转动的圈数多。
【点睛】关键是掌握圆的周长公式,圆的周长=πd,终点时间-起点时间=经过时间。
20.5cm
【详解】C内=2πr内=31.4
r内=31.4÷3.14÷2=5(cm)
C外=2πr外=62.8
r外=62.8÷3.14÷2=10(cm)
r外-r内=10-5=5(cm)
21.(1)11.51m
(2)6小时
【分析】(1)因为时针走一圈是12小时,当大本钟的时针经过8小时即是走了圆周长的,求走过的路程即是求以275米为半径的圆周长的即可;
(2)如果这个时钟的时针尖端走过的路程是8.635m,则时针走过了几小时,用走过的路程除以周长,结果即是时针走过的时间与12小时的分率,据此解答。
【详解】(1)3.14×2.75×2×
=8.635×2×
=17.27×
≈11.51(m)
答:时针的尖端走过的路程是11.51米。
(2)8.635÷(3.14×2.75×2)×12
=8.635÷17.27×12
=0.5×12
=6(小时)
答:时针走过了6小时。
【点睛】此题考查的是圆周长在实际生活中的应用,关键是把实际问题转化成数学问题进行解答。
22.20096元
【分析】根据题意,用圆形环岛的面积减去中间圆形花坛的面积就是草坪的占地面积,再用草坪的占地面积乘每平方米草皮的单价,即可求出铺满这个环形草坪买草皮需要的钱数。
【详解】60÷2=30(米)
20÷2=10(米)
3.14×(302-102)×8
=3.14×(900-100)×8
=3.14×800×8
=2512×8
=20096(元)
答:铺满这个环形草坪买草皮需要20096元钱。
【点睛】本题主要考查圆环的面积的计算方法,即大圆的面积减去小圆的面积。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
