2023-2024学年北师大版数学九年级上册1.1.2菱形的判定课件(19张ppt)
文档属性
| 名称 | 2023-2024学年北师大版数学九年级上册1.1.2菱形的判定课件(19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 13:30:09 | ||
图片预览






文档简介
(共19张PPT)
1.2 菱形的判定
1. 掌握菱形的判定方法;
2.能运用菱形的判定方法解题。
学习目标:(1分钟)
自学指导1:(8分钟)
(一)认真阅读P5-6的内容,思考并完成:
1.根据定义可知:
的平行四边形叫做菱形;
2.阅读“议一议”之前的内容,你能得到菱形的什么判定方法?
A
B
D
O
C
有一组邻边相等
已知:在口ABCD中,AC ⊥ BD
A
B
C
D
求证:口ABCD是菱形
证明:
∴口ABCD是菱形
又∵ AC ⊥ BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
数学语言:
∵四边形ABCD是平行四边形; AC ⊥ BD;
∴ □ ABCD是菱形
O
方法2:对角线互相垂直的平行四边形是菱形.
自学指导二:认真阅读P5-6的“议一议”,在课本上完成定理的证明
命题:有四条边相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
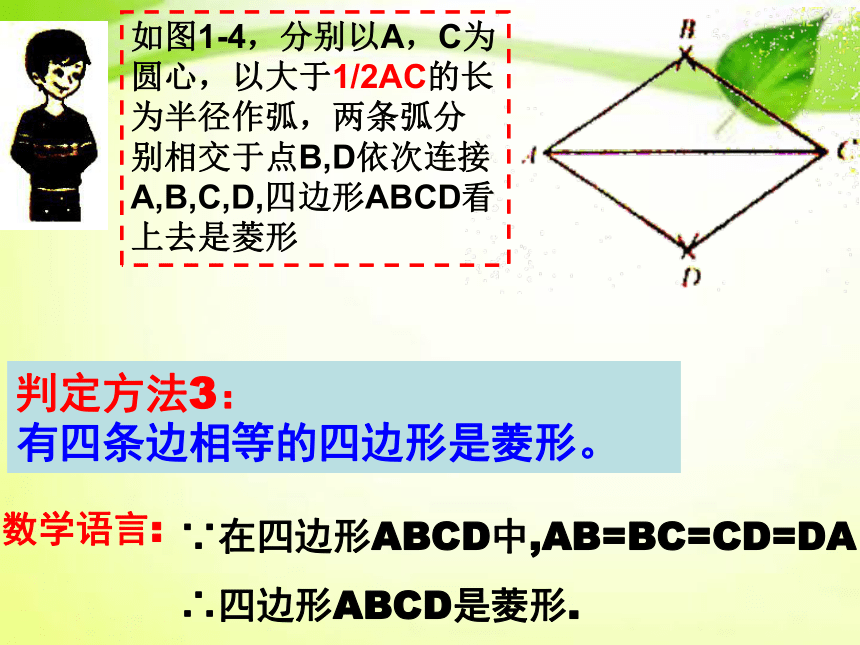
判定方法3:
有四条边相等的四边形是菱形。
数学语言:
∵在四边形ABCD中,AB=BC=CD=DA
∴四边形ABCD是菱形.
如图1-4,分别以A,C为圆心,以大于1/2AC的长为半径作弧,两条弧分别相交于点B,D依次连接A,B,C,D,四边形ABCD看上去是菱形
归纳 菱形的判定方法:
A
B
D
C
O
1. 的 是菱形。
几何语言:∵四边形ABCD是平行四边形且AB=AD,
∴四边形ABCD是菱形
2. 都相等的 是菱形。
几何语言:∵AB=BC=CD=AD
∴四边形ABCD是菱形
3. 的 是菱形。
几何语言:∵ 四边形ABCD是平行四边形且 AC⊥BD,
∴四边形ABCD是菱形
对角线
边
平行四边形
平行四边形
一组邻边相等
四条边
四边形
对角线垂直
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
做一做:
自学检测1:(10分钟)
1.如图,若四边形ABCD为平行四边形,则需加条件 ,才能使四边形ABCD为菱形。
A
B
D
C
O
2.已知口ABCD的对角线AC、BD相交于点O,则下列条件不能判定口ABCD为菱形的是( )
A.AB=AD B.AC⊥BD C.∠BAD=∠CDA D.CA平分∠BCD
证明:在△AOB中,
∴AB2=OA2+OB2
∴△AOB是直角三角形.
∴AC⊥BD
∴□ABCD是菱形
∵ AB= √5,OA=2,OB=1
认真阅读课本P6的例2,
自学指导2:(5分钟)
完成P7的知识技能-1T,2T;
自学检测2:(10分钟)完成习题1.2
3.在四边形纸片ABCD中,AD∥BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD边上的点C′处,折痕DE交BC于点E,连接C′E,你能确定四边形CDC′E的形状吗?证明你的结论。
四边形CDC′E是菱形.
理由:根据折叠的性质,可得:CD=C′D,
∠C′DE=∠CDE,CE=C′E.
∵AD∥BC,
∴∠C′DE=∠CED.
∴∠CDE=∠CED.
∴CD=CE.
∴CD=C′D=C′E=CE.
∴四边形CDC′E为菱形.
1.已知:如图,在□ABCD中,AE平分∠BAD,与BC相交于点E,EF∥AB,与AD相交于点F , 求证:四边形ABEF是菱形.
2.已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
判断四边形AEDF的形状。
3
2
1
A
B
C
D
E
F
求证:EF⊥AD
当堂训练
3.已知如图,在△ABC中,∠BAC=900,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E, EF⊥BC于F,那么形成的四边形AEFG是什么四边形?并说明理由。
D
B
A
C
E
G
F
1.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.
中考链接:
2.已知:如图,在 ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形 请说明理由.
3.如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.
(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
文字语言 图形语言 符号语言
判定法一
判定 法二 对角线互相垂直的平行四边形是菱形
判定法三 四边相等的四边形是菱形
菱形的判定:
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
一组邻边相等的平行四边形是菱形
1.2 菱形的判定
1. 掌握菱形的判定方法;
2.能运用菱形的判定方法解题。
学习目标:(1分钟)
自学指导1:(8分钟)
(一)认真阅读P5-6的内容,思考并完成:
1.根据定义可知:
的平行四边形叫做菱形;
2.阅读“议一议”之前的内容,你能得到菱形的什么判定方法?
A
B
D
O
C
有一组邻边相等
已知:在口ABCD中,AC ⊥ BD
A
B
C
D
求证:口ABCD是菱形
证明:
∴口ABCD是菱形
又∵ AC ⊥ BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
数学语言:
∵四边形ABCD是平行四边形; AC ⊥ BD;
∴ □ ABCD是菱形
O
方法2:对角线互相垂直的平行四边形是菱形.
自学指导二:认真阅读P5-6的“议一议”,在课本上完成定理的证明
命题:有四条边相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
判定方法3:
有四条边相等的四边形是菱形。
数学语言:
∵在四边形ABCD中,AB=BC=CD=DA
∴四边形ABCD是菱形.
如图1-4,分别以A,C为圆心,以大于1/2AC的长为半径作弧,两条弧分别相交于点B,D依次连接A,B,C,D,四边形ABCD看上去是菱形
归纳 菱形的判定方法:
A
B
D
C
O
1. 的 是菱形。
几何语言:∵四边形ABCD是平行四边形且AB=AD,
∴四边形ABCD是菱形
2. 都相等的 是菱形。
几何语言:∵AB=BC=CD=AD
∴四边形ABCD是菱形
3. 的 是菱形。
几何语言:∵ 四边形ABCD是平行四边形且 AC⊥BD,
∴四边形ABCD是菱形
对角线
边
平行四边形
平行四边形
一组邻边相等
四条边
四边形
对角线垂直
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
做一做:
自学检测1:(10分钟)
1.如图,若四边形ABCD为平行四边形,则需加条件 ,才能使四边形ABCD为菱形。
A
B
D
C
O
2.已知口ABCD的对角线AC、BD相交于点O,则下列条件不能判定口ABCD为菱形的是( )
A.AB=AD B.AC⊥BD C.∠BAD=∠CDA D.CA平分∠BCD
证明:在△AOB中,
∴AB2=OA2+OB2
∴△AOB是直角三角形.
∴AC⊥BD
∴□ABCD是菱形
∵ AB= √5,OA=2,OB=1
认真阅读课本P6的例2,
自学指导2:(5分钟)
完成P7的知识技能-1T,2T;
自学检测2:(10分钟)完成习题1.2
3.在四边形纸片ABCD中,AD∥BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD边上的点C′处,折痕DE交BC于点E,连接C′E,你能确定四边形CDC′E的形状吗?证明你的结论。
四边形CDC′E是菱形.
理由:根据折叠的性质,可得:CD=C′D,
∠C′DE=∠CDE,CE=C′E.
∵AD∥BC,
∴∠C′DE=∠CED.
∴∠CDE=∠CED.
∴CD=CE.
∴CD=C′D=C′E=CE.
∴四边形CDC′E为菱形.
1.已知:如图,在□ABCD中,AE平分∠BAD,与BC相交于点E,EF∥AB,与AD相交于点F , 求证:四边形ABEF是菱形.
2.已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
判断四边形AEDF的形状。
3
2
1
A
B
C
D
E
F
求证:EF⊥AD
当堂训练
3.已知如图,在△ABC中,∠BAC=900,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E, EF⊥BC于F,那么形成的四边形AEFG是什么四边形?并说明理由。
D
B
A
C
E
G
F
1.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.
中考链接:
2.已知:如图,在 ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形 请说明理由.
3.如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.
(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
文字语言 图形语言 符号语言
判定法一
判定 法二 对角线互相垂直的平行四边形是菱形
判定法三 四边相等的四边形是菱形
菱形的判定:
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
一组邻边相等的平行四边形是菱形
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
