2024河南中考数学专题复习第四章 第四节 全等、相似三角形的性质与判定 课件(共39张PPT)
文档属性
| 名称 | 2024河南中考数学专题复习第四章 第四节 全等、相似三角形的性质与判定 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 14:09:20 | ||
图片预览





文档简介
(共39张PPT)
一题串讲重难点
2
1
考点精讲
第四节 全等、相似三角形的性质与判定
课标要求
1. 理解全等三角形的概念,能识别全等三角形中的对应边、对应角;
2. 掌握基本事实:两边及其夹角分别相等的两个三角形全等;
3. 掌握基本事实:两角及其夹边分别相等的两个三角形全等;
4. 掌握基本事实:三边分别相等的两个三角形全等;
5. 证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等;
6. 探索并掌握判定直角三角形全等的“斜边、直角边”定理.
命题点1 全等三角形的性质与判定(9年13考)
考情及趋势分析
考情分析 年份 题号 题型 分值 考查内容 判定方法
2023 14 填空题 3 已知三角形的三边相等 SSS
2023 18 解答题 9 已知三角形的两边及其夹角相等 SAS
2022 23(2)(3) 解答题 7 已知直角三角形的一条直角边与斜边相等 HL
2021 23(1)(2) 解答题 7 已知直角三角形的一条直角边与斜边相等,三角形的三条边相等 HL,SAS
2020 20 解答题 9 已知三角形的两边及其夹角相等 SAS
2020 22(1)② 解答题 2 已知三角形的一条边和一个角相等,需证明另一个角或另一条边相等 AAS/ASA
2019 17(1) 解答题 5 已知三角形的一个角相等,需证明一条边及另一个角相等 ASA
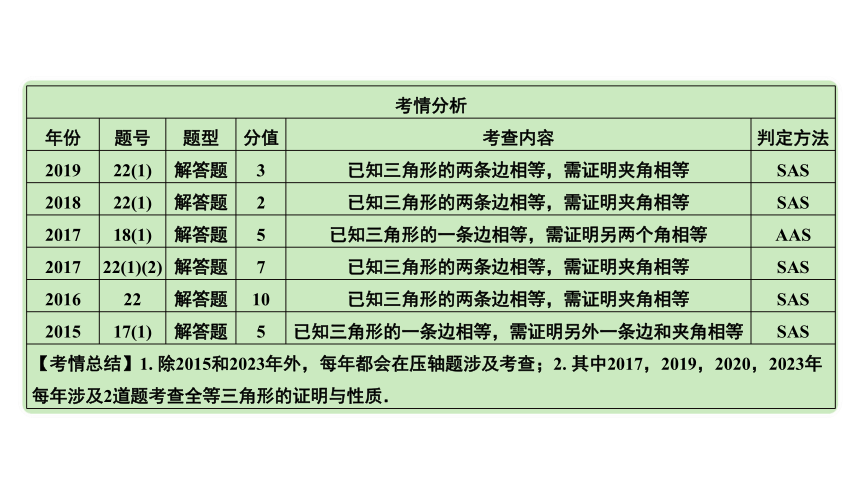
考情分析 年份 题号 题型 分值 考查内容 判定方法
2019 22(1) 解答题 3 已知三角形的两条边相等,需证明夹角相等 SAS
2018 22(1) 解答题 2 已知三角形的两条边相等,需证明夹角相等 SAS
2017 18(1) 解答题 5 已知三角形的一条边相等,需证明另两个角相等 AAS
2017 22(1)(2) 解答题 7 已知三角形的两条边相等,需证明夹角相等 SAS
2016 22 解答题 10 已知三角形的两条边相等,需证明夹角相等 SAS
2015 17(1) 解答题 5 已知三角形的一条边相等,需证明另外一条边和夹角相等 SAS
【考情总结】1. 除2015和2023年外,每年都会在压轴题涉及考查;2. 其中2017,2019,2020,2023年每年涉及2道题考查全等三角形的证明与性质.
课标要求
1. 通过具体实例认识图形的相似.了解相似多边形和相似比;
2. 掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例;
3. 了解相似三角形的判定定理:两角分别相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似.*了解相似三角形判定定理的证明;
4. 了解相似三角形的性质定理:相似三角形对应线段的比等于相似比;面积比等于相似比的平方;
5. 了解图形的位似,知道利用位似可以将一个图形放大或缩小.
命题点2 相似三角形的性质与判定(9年9考)
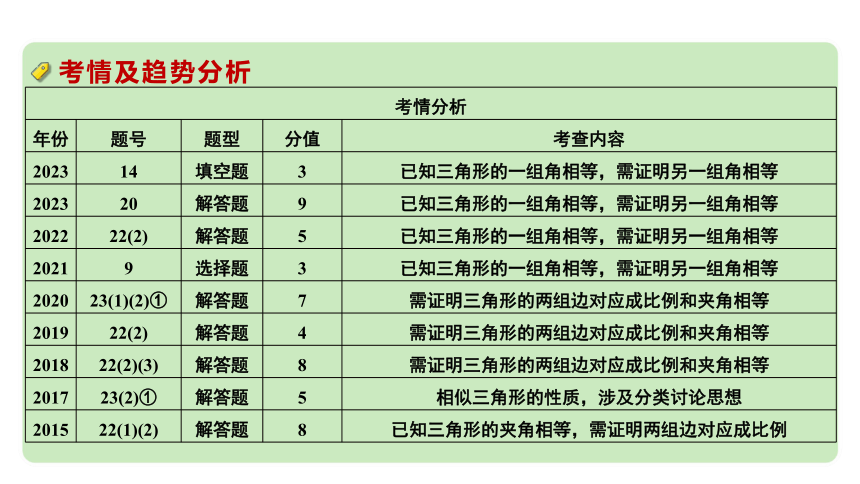
考情及趋势分析
考情分析 年份 题号 题型 分值 考查内容
2023 14 填空题 3 已知三角形的一组角相等,需证明另一组角相等
2023 20 解答题 9 已知三角形的一组角相等,需证明另一组角相等
2022 22(2) 解答题 5 已知三角形的一组角相等,需证明另一组角相等
2021 9 选择题 3 已知三角形的一组角相等,需证明另一组角相等
2020 23(1)(2)① 解答题 7 需证明三角形的两组边对应成比例和夹角相等
2019 22(2) 解答题 4 需证明三角形的两组边对应成比例和夹角相等
2018 22(2)(3) 解答题 8 需证明三角形的两组边对应成比例和夹角相等
2017 23(2)① 解答题 5 相似三角形的性质,涉及分类讨论思想
2015 22(1)(2) 解答题 8 已知三角形的夹角相等,需证明两组边对应成比例
【考情总结】
1. 仅 2016 年未考查,2021 年在选择题考查,2023年在填空题考查,其他年份均在解答题考查;
2. 除2016,2021,2023年,其余年份每年都会在压轴题涉及考查相似三角形的判定与性质;
3. 三边对应成比例,暂时未考.
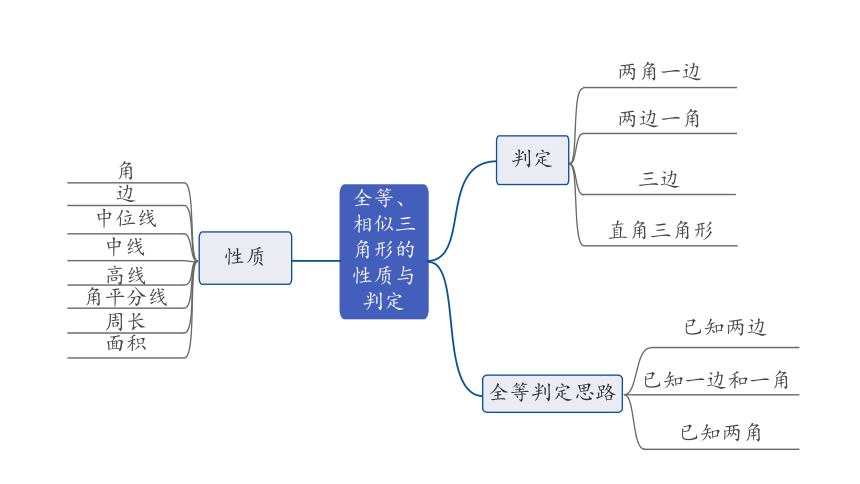
全等、
相似三
角形的
性质与
判定
性质
边
中位线
角平分线
周长
中线
角
高线
面积
两角一边
两边一角
三边
直角三角形
判定
全等判定思路
已知两边
已知两角
已知一边和一角
考点精讲
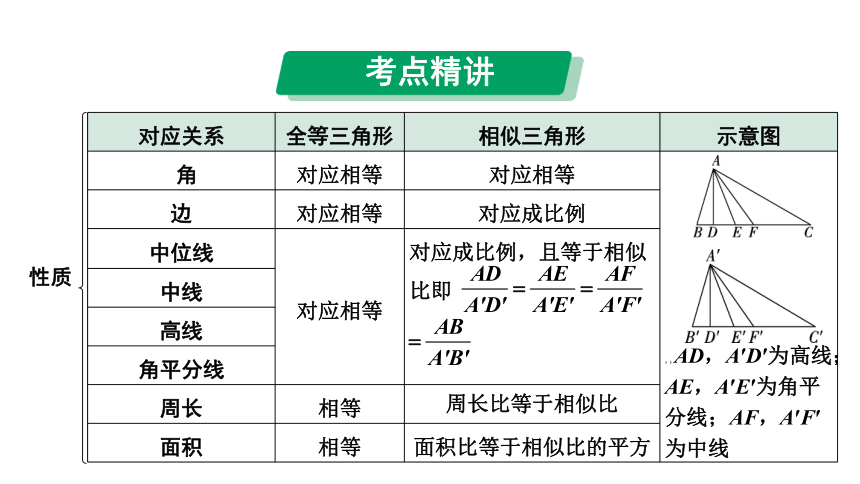
性质
对应关系 全等三角形 相似三角形 示意图
角 对应相等 对应相等 ,,AD,A′D′为高线;AE,A′E′为角平分线;AF,A′F′为中线
边 对应相等 对应成比例 中位线 对应相等 对应成比例,且等于相似比即 中线 高线 角平分线 周长 相等 周长比等于相似比 面积 相等 面积比等于相似比的平方
判定
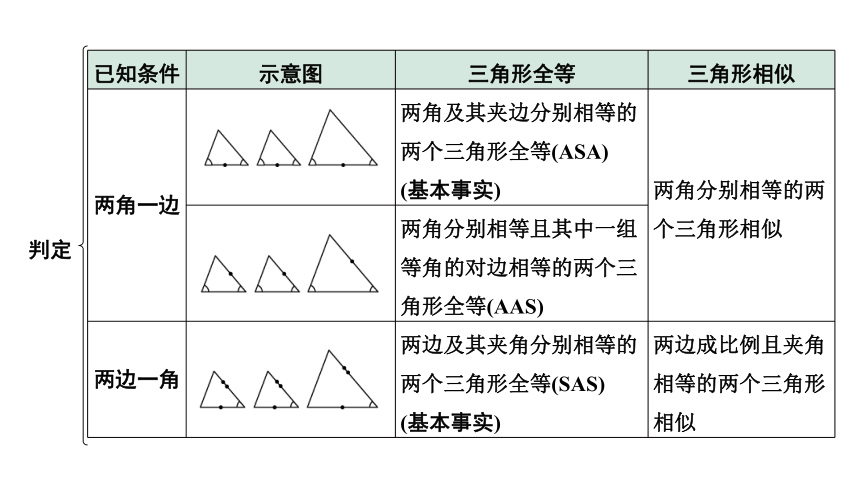
已知条件 示意图 三角形全等 三角形相似
两角一边 两角及其夹边分别相等的两个三角形全等(ASA) (基本事实) 两角分别相等的两个三角形相似
两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS) 两边一角 两边及其夹角分别相等的两个三角形全等(SAS) (基本事实) 两边成比例且夹角相等的两个三角形相似
判定
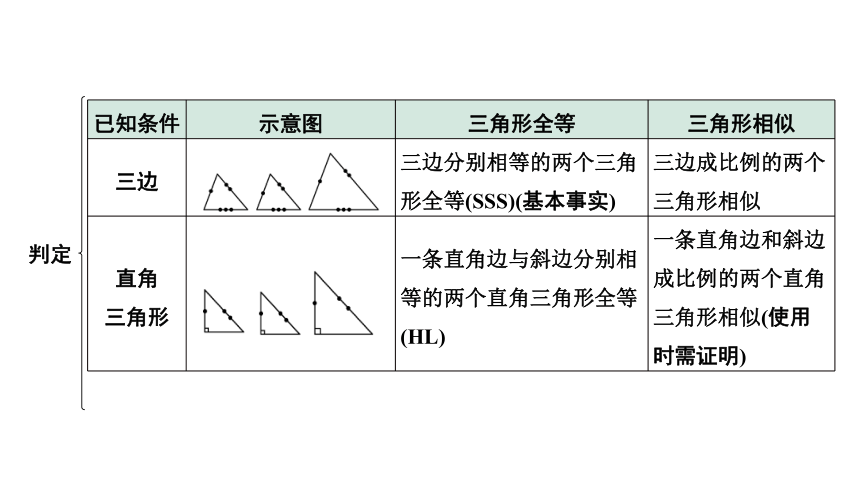
已知条件 示意图 三角形全等 三角形相似
三边 三边分别相等的两个三角形全等(SSS)(基本事实) 三边成比例的两个三角形相似
直角 三角形 一条直角边与斜边分别相等的两个直角三角形全等(HL) 一条直角边和斜边成比例的两个直角三角形相似(使用时需证明)
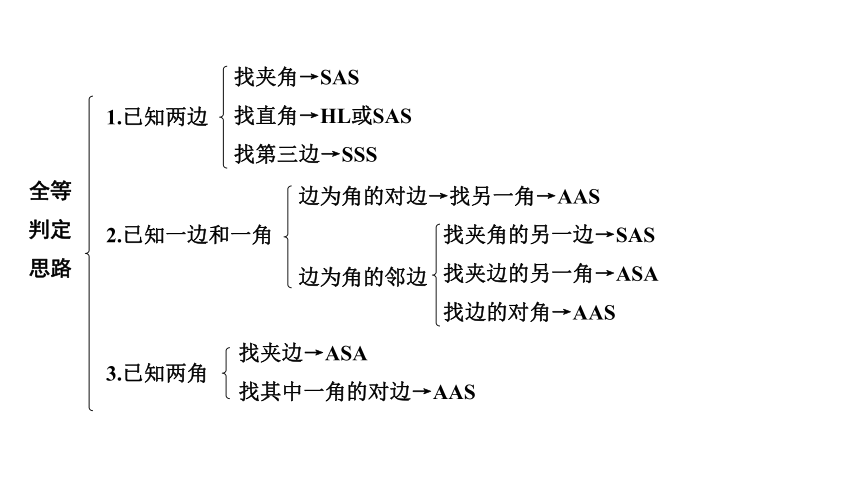
全等判定思路
1.已知两边
找夹角→SAS
找直角→HL或SAS
找第三边→SSS
2.已知一边和一角
边为角的对边→找另一角→AAS
边为角的邻边
找夹角的另一边→SAS
找夹边的另一角→ASA
找边的对角→AAS
3.已知两角
找夹边→ASA
找其中一角的对边→AAS
一题串讲重难点
全等模型分析
平移型
旋转型
对称型 有公共边
有公共顶点
解题 思路 (1)找等边:公共边、中点、等底角、相等边、通过线段和差关系得对应边相等;
(2)找等角:公共角、对顶角、垂直找直角、等腰得等角、平行线的性质得等角等.
全等三角形的简单模型
例1 如图,已知△ABC和△DEF,且点B,E,C,F在同一直线上.AC交DE于点H,已知∠B=∠DEF,∠ACB=∠DFE.
(1)请找出图中的相似三角形并说明依据;
例1题图
一题多解法
解:(1)△ABC∽△HEC;
依据:两角分别相等的两个三角形相似;
△EHC∽△EDF;
依据:两角分别相等的两个三角形相似;
△ABC∽△DEF,
依据:两角分别相等的两个三角形相似;
(2)请添加一个条件,使得△ABC≌△DEF,并写出证明过程及依据.
例1题图
(2)方法一:添加条件BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
依据:两角及其夹边分别相等的两个三角形全等;
方法二:添加条件AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
依据:两角分别相等且其中一组等角的对边相等
的两个三角形全等;
例1题图
方法三:添加条件AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
依据:两角分别相等且其中一组等角的对边相等的
两个三角形全等.(答案不唯一,选一种即可)
例1题图
变式1 改变△DEF放置方式
如图,如果将△ABC和△DEF如图放置.
一题多解法
(1)已知 ,请添加一个条件,使得△ABC∽△EDF,并选择一个写出证明过程及依据;
变式1题图
解:(1)方法一:添加条件∠A=∠FED,
∵ = ,∠A=∠FED,
∴△ABC∽△EDF,依据:两边成比例且夹角相等
的两个三角形相似;
方法二:添加条件 = ,
∵ = = ,
∴△ABC∽△EDF,依据:三边成比例的两个三角形相似;(答案不唯一,选一种即可)
变式1题图
(2)已知AB=DE,AC=EF(即 =1),请添加一个条件,使得△ABC≌△EDF,并写出证明过程及依据.
变式1题图
(2)方法一:添加条件∠A=∠FED,
∵∠A=∠FED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SAS),依据:两边及其夹角
分别相等的两个三角形全等;
方法二:添加条件BC=DF,
∵BC=DF,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS),依据:三边分别相等的
两个三角形全等.(答案不唯一,选一种即可)
变式1题图
相似模型分析
A字型
8字型
解题 思路 (1)找等角:找同侧(或异侧)的一组角相等、有平行线的截线用平行线的性质找等角;
(2)找对应边:有等角,找等角的两边对应成比例.
相似三角形的简单模型
例2 如图,已知△ABC和△ADE,且点B,A,D在同一直线上,点C,A,E在同一直线上,若∠BAC=∠DAE=90°.
(1)请添加一个条件,使得△ABC∽△ADE,并选择一个写出证明过程及依据;
一题多解法
例2题图
解:(1)方法一:添加条件∠B=∠D,
∵∠B=∠D,∠BAC=∠DAE,
∴△ABC∽△ADE,依据:两角分别相等的两个三角形相似;
方法二:添加条件∠C=∠E,
∵∠C=∠E,∠BAC=∠DAE,
∴△ABC∽△ADE,依据:两角分别相等的两个三角形相似;
例2题图
方法三:添加条件 = ,
∵ = ,∠BAC=∠DAE,
∴△ABC∽△ADE,依据:两边成比例且夹角相等
的两个三角形相似;(答案不唯一,选一种即可)
(2)已知AB=AD,请添加一个条件,使得△ABC≌△ADE,并写出证明过程及依据.
例2题图
(2)方法一:添加条件AC=AE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS),
依据:两边及其夹角分别相等的两个三角形全等;
一题多解法
思路点拨:
解法二:添加条件∠B=∠D,依据:ASA;
解法三:添加条件∠C=∠E,依据:AAS;
解法四:添加条件BC=DE,依据:HL.
方法二:添加条件∠B=∠D,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA),
依据:两角及其夹边分别相等的两个三角形全等;
例2题图
方法三:添加条件∠C=∠E,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
依据:两角分别相等且其中一组等角的对边相等的两个三角形全等;
例2题图
例2题图
方法四:添加条件BC=DE,
在Rt△ABC和Rt△ADE中,
,
∴△ABC≌△ADE(HL),
依据:一条直角边与斜边分别相等的两个直角三角形全等.(答案不唯一,选一种即可)
例3 如图,在△ABC中,点D是AB上的点,点E是AC上的点,连接CD与BE交于点F.
(1)请添加一个条件,使得△BFD∽△CFE,并选择一个写出证明过程及依据;
一题多解法
例3题图
解:(1)方法一:添加条件∠BDF=∠CEF,
∵∠BDF=∠CEF,∠BFD=∠CFE,
∴△BFD∽△CFE,依据:两角分别相等的两个三角形相似;
方法二:添加条件∠DBF=∠ECF,
∵∠DBF=∠ECF,∠BFD=∠CFE,
∴△BFD∽△CFE,依据:两角分别相等的两个三角形相似;
例3题图
方法三:添加条件 = ,
∵ = ,∠BFD=∠CFE,
∴△BFD∽△CFE,依据:两边成比例且夹角相等
的两个三角形相似;(答案不唯一,选一种即可)
(2)已知BD=CE,请添加一个条件,使得△BDF≌△CEF,并写出证明过程及依据.若BF=3,求CF的长.
例3题图
(2)方法一:添加条件∠BDF=∠CEF,
∵∠BDF=∠CEF,
在△BDF和△CEF中,
,
∴△BDF≌△CEF(AAS),依据:两角分别相等且其中
一组等角的对边相等的两个三角形全等;
∴CF=BF=3;
一题多解法
解法:添加条件∠DBF=∠ECF,依据:AAS.
例3题图
方法二:添加条件∠DBF=∠ECF,
∵∠DBF=∠ECF,
在△BDF和△CEF中,
,
∴△BDF≌△CEF(AAS),
依据:两角分别相等且其中一组等角的对边相等的
两个三角形全等;
∴CF=BF=3.(答案不唯一,选一种即可)
请完成精练本习题
一题串讲重难点
2
1
考点精讲
第四节 全等、相似三角形的性质与判定
课标要求
1. 理解全等三角形的概念,能识别全等三角形中的对应边、对应角;
2. 掌握基本事实:两边及其夹角分别相等的两个三角形全等;
3. 掌握基本事实:两角及其夹边分别相等的两个三角形全等;
4. 掌握基本事实:三边分别相等的两个三角形全等;
5. 证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等;
6. 探索并掌握判定直角三角形全等的“斜边、直角边”定理.
命题点1 全等三角形的性质与判定(9年13考)
考情及趋势分析
考情分析 年份 题号 题型 分值 考查内容 判定方法
2023 14 填空题 3 已知三角形的三边相等 SSS
2023 18 解答题 9 已知三角形的两边及其夹角相等 SAS
2022 23(2)(3) 解答题 7 已知直角三角形的一条直角边与斜边相等 HL
2021 23(1)(2) 解答题 7 已知直角三角形的一条直角边与斜边相等,三角形的三条边相等 HL,SAS
2020 20 解答题 9 已知三角形的两边及其夹角相等 SAS
2020 22(1)② 解答题 2 已知三角形的一条边和一个角相等,需证明另一个角或另一条边相等 AAS/ASA
2019 17(1) 解答题 5 已知三角形的一个角相等,需证明一条边及另一个角相等 ASA
考情分析 年份 题号 题型 分值 考查内容 判定方法
2019 22(1) 解答题 3 已知三角形的两条边相等,需证明夹角相等 SAS
2018 22(1) 解答题 2 已知三角形的两条边相等,需证明夹角相等 SAS
2017 18(1) 解答题 5 已知三角形的一条边相等,需证明另两个角相等 AAS
2017 22(1)(2) 解答题 7 已知三角形的两条边相等,需证明夹角相等 SAS
2016 22 解答题 10 已知三角形的两条边相等,需证明夹角相等 SAS
2015 17(1) 解答题 5 已知三角形的一条边相等,需证明另外一条边和夹角相等 SAS
【考情总结】1. 除2015和2023年外,每年都会在压轴题涉及考查;2. 其中2017,2019,2020,2023年每年涉及2道题考查全等三角形的证明与性质.
课标要求
1. 通过具体实例认识图形的相似.了解相似多边形和相似比;
2. 掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例;
3. 了解相似三角形的判定定理:两角分别相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似.*了解相似三角形判定定理的证明;
4. 了解相似三角形的性质定理:相似三角形对应线段的比等于相似比;面积比等于相似比的平方;
5. 了解图形的位似,知道利用位似可以将一个图形放大或缩小.
命题点2 相似三角形的性质与判定(9年9考)
考情及趋势分析
考情分析 年份 题号 题型 分值 考查内容
2023 14 填空题 3 已知三角形的一组角相等,需证明另一组角相等
2023 20 解答题 9 已知三角形的一组角相等,需证明另一组角相等
2022 22(2) 解答题 5 已知三角形的一组角相等,需证明另一组角相等
2021 9 选择题 3 已知三角形的一组角相等,需证明另一组角相等
2020 23(1)(2)① 解答题 7 需证明三角形的两组边对应成比例和夹角相等
2019 22(2) 解答题 4 需证明三角形的两组边对应成比例和夹角相等
2018 22(2)(3) 解答题 8 需证明三角形的两组边对应成比例和夹角相等
2017 23(2)① 解答题 5 相似三角形的性质,涉及分类讨论思想
2015 22(1)(2) 解答题 8 已知三角形的夹角相等,需证明两组边对应成比例
【考情总结】
1. 仅 2016 年未考查,2021 年在选择题考查,2023年在填空题考查,其他年份均在解答题考查;
2. 除2016,2021,2023年,其余年份每年都会在压轴题涉及考查相似三角形的判定与性质;
3. 三边对应成比例,暂时未考.
全等、
相似三
角形的
性质与
判定
性质
边
中位线
角平分线
周长
中线
角
高线
面积
两角一边
两边一角
三边
直角三角形
判定
全等判定思路
已知两边
已知两角
已知一边和一角
考点精讲
性质
对应关系 全等三角形 相似三角形 示意图
角 对应相等 对应相等 ,,AD,A′D′为高线;AE,A′E′为角平分线;AF,A′F′为中线
边 对应相等 对应成比例 中位线 对应相等 对应成比例,且等于相似比即 中线 高线 角平分线 周长 相等 周长比等于相似比 面积 相等 面积比等于相似比的平方
判定
已知条件 示意图 三角形全等 三角形相似
两角一边 两角及其夹边分别相等的两个三角形全等(ASA) (基本事实) 两角分别相等的两个三角形相似
两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS) 两边一角 两边及其夹角分别相等的两个三角形全等(SAS) (基本事实) 两边成比例且夹角相等的两个三角形相似
判定
已知条件 示意图 三角形全等 三角形相似
三边 三边分别相等的两个三角形全等(SSS)(基本事实) 三边成比例的两个三角形相似
直角 三角形 一条直角边与斜边分别相等的两个直角三角形全等(HL) 一条直角边和斜边成比例的两个直角三角形相似(使用时需证明)
全等判定思路
1.已知两边
找夹角→SAS
找直角→HL或SAS
找第三边→SSS
2.已知一边和一角
边为角的对边→找另一角→AAS
边为角的邻边
找夹角的另一边→SAS
找夹边的另一角→ASA
找边的对角→AAS
3.已知两角
找夹边→ASA
找其中一角的对边→AAS
一题串讲重难点
全等模型分析
平移型
旋转型
对称型 有公共边
有公共顶点
解题 思路 (1)找等边:公共边、中点、等底角、相等边、通过线段和差关系得对应边相等;
(2)找等角:公共角、对顶角、垂直找直角、等腰得等角、平行线的性质得等角等.
全等三角形的简单模型
例1 如图,已知△ABC和△DEF,且点B,E,C,F在同一直线上.AC交DE于点H,已知∠B=∠DEF,∠ACB=∠DFE.
(1)请找出图中的相似三角形并说明依据;
例1题图
一题多解法
解:(1)△ABC∽△HEC;
依据:两角分别相等的两个三角形相似;
△EHC∽△EDF;
依据:两角分别相等的两个三角形相似;
△ABC∽△DEF,
依据:两角分别相等的两个三角形相似;
(2)请添加一个条件,使得△ABC≌△DEF,并写出证明过程及依据.
例1题图
(2)方法一:添加条件BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
依据:两角及其夹边分别相等的两个三角形全等;
方法二:添加条件AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
依据:两角分别相等且其中一组等角的对边相等
的两个三角形全等;
例1题图
方法三:添加条件AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
依据:两角分别相等且其中一组等角的对边相等的
两个三角形全等.(答案不唯一,选一种即可)
例1题图
变式1 改变△DEF放置方式
如图,如果将△ABC和△DEF如图放置.
一题多解法
(1)已知 ,请添加一个条件,使得△ABC∽△EDF,并选择一个写出证明过程及依据;
变式1题图
解:(1)方法一:添加条件∠A=∠FED,
∵ = ,∠A=∠FED,
∴△ABC∽△EDF,依据:两边成比例且夹角相等
的两个三角形相似;
方法二:添加条件 = ,
∵ = = ,
∴△ABC∽△EDF,依据:三边成比例的两个三角形相似;(答案不唯一,选一种即可)
变式1题图
(2)已知AB=DE,AC=EF(即 =1),请添加一个条件,使得△ABC≌△EDF,并写出证明过程及依据.
变式1题图
(2)方法一:添加条件∠A=∠FED,
∵∠A=∠FED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SAS),依据:两边及其夹角
分别相等的两个三角形全等;
方法二:添加条件BC=DF,
∵BC=DF,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS),依据:三边分别相等的
两个三角形全等.(答案不唯一,选一种即可)
变式1题图
相似模型分析
A字型
8字型
解题 思路 (1)找等角:找同侧(或异侧)的一组角相等、有平行线的截线用平行线的性质找等角;
(2)找对应边:有等角,找等角的两边对应成比例.
相似三角形的简单模型
例2 如图,已知△ABC和△ADE,且点B,A,D在同一直线上,点C,A,E在同一直线上,若∠BAC=∠DAE=90°.
(1)请添加一个条件,使得△ABC∽△ADE,并选择一个写出证明过程及依据;
一题多解法
例2题图
解:(1)方法一:添加条件∠B=∠D,
∵∠B=∠D,∠BAC=∠DAE,
∴△ABC∽△ADE,依据:两角分别相等的两个三角形相似;
方法二:添加条件∠C=∠E,
∵∠C=∠E,∠BAC=∠DAE,
∴△ABC∽△ADE,依据:两角分别相等的两个三角形相似;
例2题图
方法三:添加条件 = ,
∵ = ,∠BAC=∠DAE,
∴△ABC∽△ADE,依据:两边成比例且夹角相等
的两个三角形相似;(答案不唯一,选一种即可)
(2)已知AB=AD,请添加一个条件,使得△ABC≌△ADE,并写出证明过程及依据.
例2题图
(2)方法一:添加条件AC=AE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS),
依据:两边及其夹角分别相等的两个三角形全等;
一题多解法
思路点拨:
解法二:添加条件∠B=∠D,依据:ASA;
解法三:添加条件∠C=∠E,依据:AAS;
解法四:添加条件BC=DE,依据:HL.
方法二:添加条件∠B=∠D,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA),
依据:两角及其夹边分别相等的两个三角形全等;
例2题图
方法三:添加条件∠C=∠E,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
依据:两角分别相等且其中一组等角的对边相等的两个三角形全等;
例2题图
例2题图
方法四:添加条件BC=DE,
在Rt△ABC和Rt△ADE中,
,
∴△ABC≌△ADE(HL),
依据:一条直角边与斜边分别相等的两个直角三角形全等.(答案不唯一,选一种即可)
例3 如图,在△ABC中,点D是AB上的点,点E是AC上的点,连接CD与BE交于点F.
(1)请添加一个条件,使得△BFD∽△CFE,并选择一个写出证明过程及依据;
一题多解法
例3题图
解:(1)方法一:添加条件∠BDF=∠CEF,
∵∠BDF=∠CEF,∠BFD=∠CFE,
∴△BFD∽△CFE,依据:两角分别相等的两个三角形相似;
方法二:添加条件∠DBF=∠ECF,
∵∠DBF=∠ECF,∠BFD=∠CFE,
∴△BFD∽△CFE,依据:两角分别相等的两个三角形相似;
例3题图
方法三:添加条件 = ,
∵ = ,∠BFD=∠CFE,
∴△BFD∽△CFE,依据:两边成比例且夹角相等
的两个三角形相似;(答案不唯一,选一种即可)
(2)已知BD=CE,请添加一个条件,使得△BDF≌△CEF,并写出证明过程及依据.若BF=3,求CF的长.
例3题图
(2)方法一:添加条件∠BDF=∠CEF,
∵∠BDF=∠CEF,
在△BDF和△CEF中,
,
∴△BDF≌△CEF(AAS),依据:两角分别相等且其中
一组等角的对边相等的两个三角形全等;
∴CF=BF=3;
一题多解法
解法:添加条件∠DBF=∠ECF,依据:AAS.
例3题图
方法二:添加条件∠DBF=∠ECF,
∵∠DBF=∠ECF,
在△BDF和△CEF中,
,
∴△BDF≌△CEF(AAS),
依据:两角分别相等且其中一组等角的对边相等的
两个三角形全等;
∴CF=BF=3.(答案不唯一,选一种即可)
请完成精练本习题
同课章节目录
