2024河南中考数学专题复习第四章 微专题 遇到中点如何添加辅助线 课件(共26张PPT)
文档属性
| 名称 | 2024河南中考数学专题复习第四章 微专题 遇到中点如何添加辅助线 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 663.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 14:10:38 | ||
图片预览





文档简介
(共26张PPT)
遇到中点如何添加辅助线
微专题
一阶 方法训练
方法解读
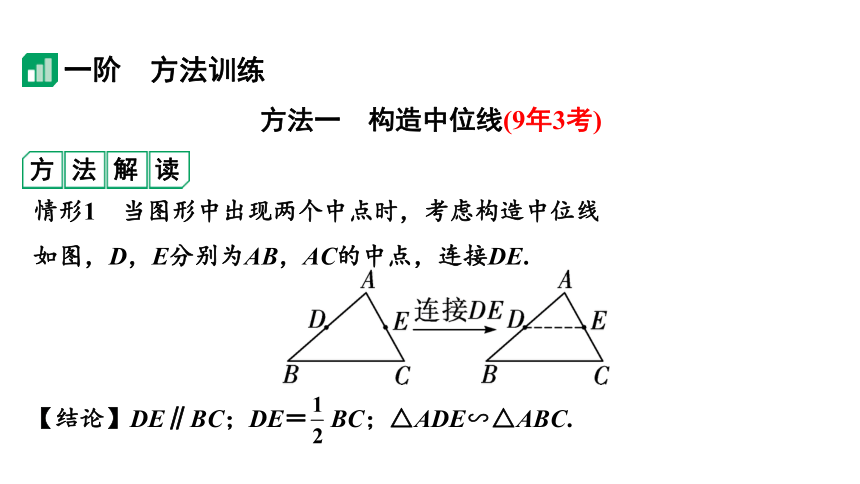
情形1 当图形中出现两个中点时,考虑构造中位线
如图,D,E分别为AB,AC的中点,连接DE.
【结论】DE∥BC;DE= BC;△ADE∽△ABC.
方法一 构造中位线(9年3考)
情形2 当图形中出现中点,考虑过中点作已知边的平行线构造中位线
如图,点D为AB的中点,过点D作DE∥BC交AC于点E.
【结论】AE=CE;DE= BC;△ADE∽△ABC.
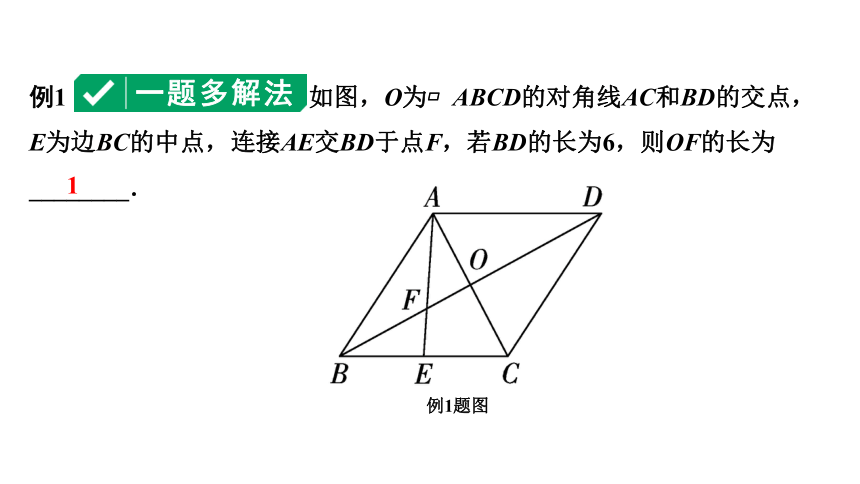
例1 如图,O为 ABCD的对角线AC和BD的交点,E为边BC的中点,连接AE交BD于点F,若BD的长为6,则OF的长为________.
一题多解法
例1题图
1
例2 如图,在△ABC中,D为AC的中点,过点D作DE⊥AC交AB于点F,交CB的延长线于点E,若F为DE的中点,BF=3,求AF的长.
一题多解法
例2题图
解法一:解:如图,过点D作DG∥AB交BC于点G,
∵点F为DE的中点,∴BF为△EGD的中位线,
∴DG=2BF=6.
∵D为AC的中点,∴DG为△ABC的中位线,
∴AB=2DG=12,
∴AF=AB-BF=12-3=9.
G
一题多解法
思路点拨:
例2
解法:如图,过点D作DH∥BC交AB于点H,证明△HDF≌△BEF.
解法二:解:如图,过点D作DH∥BC交AB于点H,
∵DH∥BC,∴∠HDF=∠E,∠FHD=∠EBF.
∵F为ED中点,∴EF=DF,
∴△HDF≌△BEF,
∴HF=FB=3,∴BH=6.
∵D为AC中点,
∴H为AB中点,
∴AH=HB=6,∴AB=12,
∴AF=AB-BF=9.
例2题图
H
方法解读
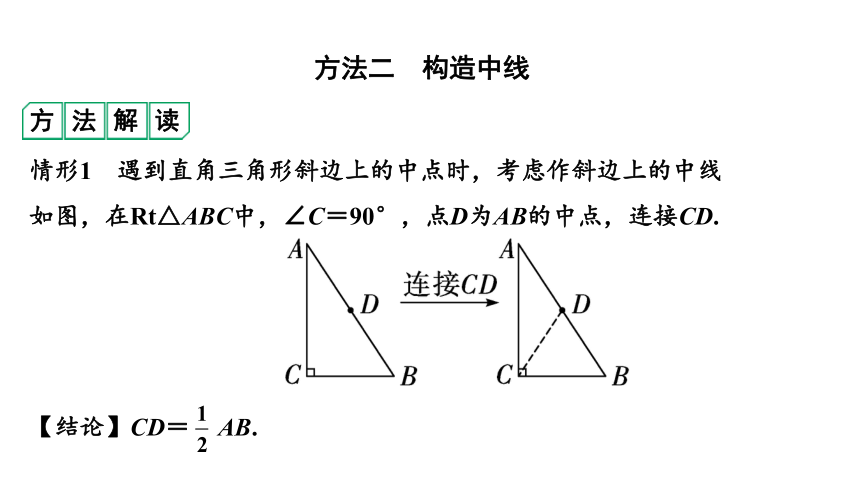
情形1 遇到直角三角形斜边上的中点时,考虑作斜边上的中线
如图,在Rt△ABC中,∠C=90°,点D为AB的中点,连接CD.
【结论】CD= AB.
方法二 构造中线
方法解读
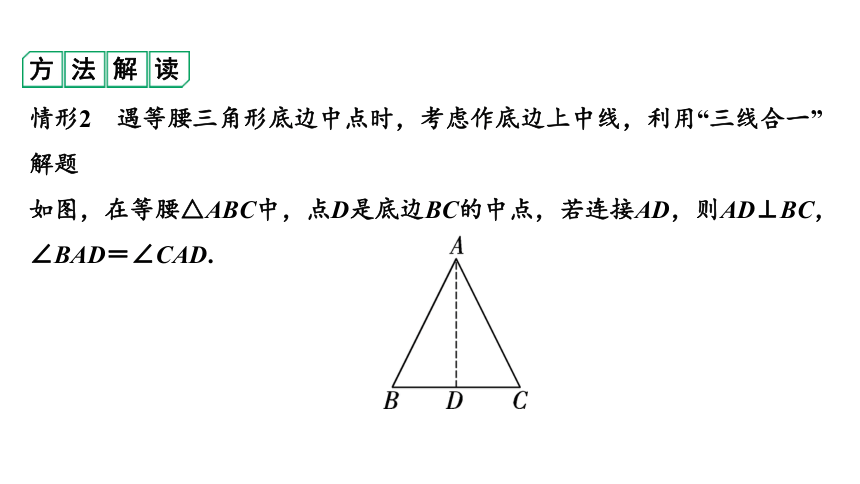
情形2 遇等腰三角形底边中点时,考虑作底边上中线,利用“三线合一”解题
如图,在等腰△ABC中,点D是底边BC的中点,若连接AD,则AD⊥BC,∠BAD=∠CAD.
例3 如图,在等腰Rt△ABC中,∠ABC=90°,D为边AC的中点,E,F分别是AB,BC边上的点,且DE⊥DF,连接EF,若AE=4,FC=3,则EF的长为________.
例3题图
5
例4 如图,将两个含30°且大小不一样的两个直角三角板(Rt△ABC和Rt△BCD)如图摆放在一起,∠ACB=∠BDC=90°,E为AB的中点,连接DE.若AC=2,则DE的长为________.
例4题图
例5 如图,在△ABC中,D是BC上的点,E,F分别是AC,BD的中点,连接AD,EF,若AD=AB,AC=6,则EF的长度为________.
例5题图
3
方法解读
①如图,AD是BC边的中线,若延长AD至点E,使得DE=AD,连接BE,则△ACD≌△EBD.
方法三 构造倍长中线
②如图,D是BC边的中点,E是AB上一点,连接ED,延长ED至点F,使得DF=ED,连接CF,则△BDE≌△CDF.
注:连接EC,ED实质为△BEC的中线.
倍长中线的本质可以理解为平移变换或中心对称.
例6 如图,AD是△ABC的中线,在AD上取一点F,连接BF并延长交AC于点E,使AE=EF,求证:BF=AC.
一题多解法
例6题图
解法一:证明:如图,延长AD至点H,使DH=AD,连接BH,
∵AD是△ABC的中线,∴BD=CD.
又∵∠ADC=∠BDH,AD=DH,
∴△ADC≌△HDB(SAS),
∴AC=BH,∠CAD=∠H.
H
∵AE=EF,
∴∠EAF=∠AFE.
∵∠AFE=∠BFH,
∴∠H=∠BFH,
∴BF=BH,
∴BF=AC.
例6题图
H
解法二:证明:如图,延长FD到点G,使DG=DF,连接CG,
∵AD是△ABC的中线,∴BD=CD.
在△BDF和△CDG中, ,
∴△BDF≌△CDG(SAS),
∴BF=CG,∠BFD=∠G.
∵AE=EF,∴∠EAF=∠EFA=∠BFD,
∴∠G=∠CAG,
∴AC=CG,∴BF=AC.
例6题图
G
二阶 综合训练
1.如图,在Rt△ABC中,∠BAC=90°,BC=4,E,F分别是BC,AC的中点,延长BA到点D,使AD= AB,连接DE,DF,则DF的长为________.
第1题图
2
【解析】如图,连接EF,AE. ∵E,F分别为BC,AC的中点,
∴BE=EC,AF=CF,∴EF∥AB,EF= AB,
∵AD= AB,∴AD=EF,
∴四边形ADFE是平行四边形,∴DF=AE,
∵∠BAC=90°,∴AE= BC=2,∴DF=AE=2.
第2题图
2. 如图,在正方形ABCD中,AB=6,点E是BC边上一点,连接AE,作∠AEF=∠DAE,交CD于点F,若点F是CD的中点,则EF的长为________.
【解析】如图,延长EF,AD交于点G,
∵∠AEF=∠DAE,∴AG=EG.
设DG=x,则EG=AG=6+x,
∵四边形ABCD是正方形,
∴∠C=∠ADC=90°=∠GDF,AB=CD=6.
∵点F是CD的中点,∴CF=DF=3,
G
又∵∠CFE=∠DFG,∴△CEF≌△DGF,
∴CE=DG=x,EF=GF= .
在Rt△CEF中,根据勾股定理,
得CF2+CE2=EF2,
即32+x2=( )2,解得x=4或x=0(舍去),
∴EF= =5.
【答案】5
第2题图
G
解题关键点
延长EF,AD交于点G,证得△CEF≌△DGF,再根据勾股定理求解.
3. 如图,在△ABC中,AC=BC=13,AB=10,点D是AB的中点,E是AC边上一点,连接BE交CD于点F,若CE=7,求CF的长.
第3题图
解:∵AC=BC=13,D是AB的中点,
∴∠ADC=∠BDC=90°,AD=BD=5.
∵CE=7,
∴AE=AC-CE=13-7=6.
如图,过点D作DG∥AC交BE于点G,
G
∵AD=BD,∴DG是△BAE的中位线,∴DG= AE=3.
∵DG∥AC,∴△DGF∽△CEF,
∴ = ,即 = .
在Rt△BDC中,根据勾股定理,
得CD= = =12,
∴ = ,解得CF= .
第3题图
G
【解题思路】
∵AC=BC=13,D是AB的中点,可得∠ADC=∠BDC=90°,AD=BD=5,AE=AC-CE=6,如解图,过点D作DG∥BE交AC于点G,由中位线定理得AG=GE=3,CG=10,可证得△CEF∽△CGD,得出 ,由勾股定理解得CD的长,最后求出CF的长.
第3题解图
一题多解
4. 如图,在矩形ABCD中,点E在CB的延长线上,连接AE,AC,点F是AE的中点,连接DF,若AB=6,AD=8,CE=AC,求DF的长.
第4题图
解:如图,过点F作FH⊥CD交AB于点G,交CD于点H,
∵在矩形ABCD中,BC⊥CD,
∴FH∥BC,
∵F是AE的中点,
∴FG是△ABE的中位线,
∴FG= BE,AG=BG.
∟
G
H
由FH⊥CD和矩形的性质可得,DH=CH= CD= AB=3,
在Rt△ABC中,AB=6,BC=8,
∴AC=10,
∵CA=CE,BC=8,
∴BE=2,
∴FH=FG+GH= BE+BC=9,
∴在Rt△DFH中,
DF= = =3 .
第4题图
∟
G
H
解题关键点
过点F作FH⊥CD于点H,交AB于点G,证FG是△ABE的中位线.
请完成精练本习题
遇到中点如何添加辅助线
微专题
一阶 方法训练
方法解读
情形1 当图形中出现两个中点时,考虑构造中位线
如图,D,E分别为AB,AC的中点,连接DE.
【结论】DE∥BC;DE= BC;△ADE∽△ABC.
方法一 构造中位线(9年3考)
情形2 当图形中出现中点,考虑过中点作已知边的平行线构造中位线
如图,点D为AB的中点,过点D作DE∥BC交AC于点E.
【结论】AE=CE;DE= BC;△ADE∽△ABC.
例1 如图,O为 ABCD的对角线AC和BD的交点,E为边BC的中点,连接AE交BD于点F,若BD的长为6,则OF的长为________.
一题多解法
例1题图
1
例2 如图,在△ABC中,D为AC的中点,过点D作DE⊥AC交AB于点F,交CB的延长线于点E,若F为DE的中点,BF=3,求AF的长.
一题多解法
例2题图
解法一:解:如图,过点D作DG∥AB交BC于点G,
∵点F为DE的中点,∴BF为△EGD的中位线,
∴DG=2BF=6.
∵D为AC的中点,∴DG为△ABC的中位线,
∴AB=2DG=12,
∴AF=AB-BF=12-3=9.
G
一题多解法
思路点拨:
例2
解法:如图,过点D作DH∥BC交AB于点H,证明△HDF≌△BEF.
解法二:解:如图,过点D作DH∥BC交AB于点H,
∵DH∥BC,∴∠HDF=∠E,∠FHD=∠EBF.
∵F为ED中点,∴EF=DF,
∴△HDF≌△BEF,
∴HF=FB=3,∴BH=6.
∵D为AC中点,
∴H为AB中点,
∴AH=HB=6,∴AB=12,
∴AF=AB-BF=9.
例2题图
H
方法解读
情形1 遇到直角三角形斜边上的中点时,考虑作斜边上的中线
如图,在Rt△ABC中,∠C=90°,点D为AB的中点,连接CD.
【结论】CD= AB.
方法二 构造中线
方法解读
情形2 遇等腰三角形底边中点时,考虑作底边上中线,利用“三线合一”解题
如图,在等腰△ABC中,点D是底边BC的中点,若连接AD,则AD⊥BC,∠BAD=∠CAD.
例3 如图,在等腰Rt△ABC中,∠ABC=90°,D为边AC的中点,E,F分别是AB,BC边上的点,且DE⊥DF,连接EF,若AE=4,FC=3,则EF的长为________.
例3题图
5
例4 如图,将两个含30°且大小不一样的两个直角三角板(Rt△ABC和Rt△BCD)如图摆放在一起,∠ACB=∠BDC=90°,E为AB的中点,连接DE.若AC=2,则DE的长为________.
例4题图
例5 如图,在△ABC中,D是BC上的点,E,F分别是AC,BD的中点,连接AD,EF,若AD=AB,AC=6,则EF的长度为________.
例5题图
3
方法解读
①如图,AD是BC边的中线,若延长AD至点E,使得DE=AD,连接BE,则△ACD≌△EBD.
方法三 构造倍长中线
②如图,D是BC边的中点,E是AB上一点,连接ED,延长ED至点F,使得DF=ED,连接CF,则△BDE≌△CDF.
注:连接EC,ED实质为△BEC的中线.
倍长中线的本质可以理解为平移变换或中心对称.
例6 如图,AD是△ABC的中线,在AD上取一点F,连接BF并延长交AC于点E,使AE=EF,求证:BF=AC.
一题多解法
例6题图
解法一:证明:如图,延长AD至点H,使DH=AD,连接BH,
∵AD是△ABC的中线,∴BD=CD.
又∵∠ADC=∠BDH,AD=DH,
∴△ADC≌△HDB(SAS),
∴AC=BH,∠CAD=∠H.
H
∵AE=EF,
∴∠EAF=∠AFE.
∵∠AFE=∠BFH,
∴∠H=∠BFH,
∴BF=BH,
∴BF=AC.
例6题图
H
解法二:证明:如图,延长FD到点G,使DG=DF,连接CG,
∵AD是△ABC的中线,∴BD=CD.
在△BDF和△CDG中, ,
∴△BDF≌△CDG(SAS),
∴BF=CG,∠BFD=∠G.
∵AE=EF,∴∠EAF=∠EFA=∠BFD,
∴∠G=∠CAG,
∴AC=CG,∴BF=AC.
例6题图
G
二阶 综合训练
1.如图,在Rt△ABC中,∠BAC=90°,BC=4,E,F分别是BC,AC的中点,延长BA到点D,使AD= AB,连接DE,DF,则DF的长为________.
第1题图
2
【解析】如图,连接EF,AE. ∵E,F分别为BC,AC的中点,
∴BE=EC,AF=CF,∴EF∥AB,EF= AB,
∵AD= AB,∴AD=EF,
∴四边形ADFE是平行四边形,∴DF=AE,
∵∠BAC=90°,∴AE= BC=2,∴DF=AE=2.
第2题图
2. 如图,在正方形ABCD中,AB=6,点E是BC边上一点,连接AE,作∠AEF=∠DAE,交CD于点F,若点F是CD的中点,则EF的长为________.
【解析】如图,延长EF,AD交于点G,
∵∠AEF=∠DAE,∴AG=EG.
设DG=x,则EG=AG=6+x,
∵四边形ABCD是正方形,
∴∠C=∠ADC=90°=∠GDF,AB=CD=6.
∵点F是CD的中点,∴CF=DF=3,
G
又∵∠CFE=∠DFG,∴△CEF≌△DGF,
∴CE=DG=x,EF=GF= .
在Rt△CEF中,根据勾股定理,
得CF2+CE2=EF2,
即32+x2=( )2,解得x=4或x=0(舍去),
∴EF= =5.
【答案】5
第2题图
G
解题关键点
延长EF,AD交于点G,证得△CEF≌△DGF,再根据勾股定理求解.
3. 如图,在△ABC中,AC=BC=13,AB=10,点D是AB的中点,E是AC边上一点,连接BE交CD于点F,若CE=7,求CF的长.
第3题图
解:∵AC=BC=13,D是AB的中点,
∴∠ADC=∠BDC=90°,AD=BD=5.
∵CE=7,
∴AE=AC-CE=13-7=6.
如图,过点D作DG∥AC交BE于点G,
G
∵AD=BD,∴DG是△BAE的中位线,∴DG= AE=3.
∵DG∥AC,∴△DGF∽△CEF,
∴ = ,即 = .
在Rt△BDC中,根据勾股定理,
得CD= = =12,
∴ = ,解得CF= .
第3题图
G
【解题思路】
∵AC=BC=13,D是AB的中点,可得∠ADC=∠BDC=90°,AD=BD=5,AE=AC-CE=6,如解图,过点D作DG∥BE交AC于点G,由中位线定理得AG=GE=3,CG=10,可证得△CEF∽△CGD,得出 ,由勾股定理解得CD的长,最后求出CF的长.
第3题解图
一题多解
4. 如图,在矩形ABCD中,点E在CB的延长线上,连接AE,AC,点F是AE的中点,连接DF,若AB=6,AD=8,CE=AC,求DF的长.
第4题图
解:如图,过点F作FH⊥CD交AB于点G,交CD于点H,
∵在矩形ABCD中,BC⊥CD,
∴FH∥BC,
∵F是AE的中点,
∴FG是△ABE的中位线,
∴FG= BE,AG=BG.
∟
G
H
由FH⊥CD和矩形的性质可得,DH=CH= CD= AB=3,
在Rt△ABC中,AB=6,BC=8,
∴AC=10,
∵CA=CE,BC=8,
∴BE=2,
∴FH=FG+GH= BE+BC=9,
∴在Rt△DFH中,
DF= = =3 .
第4题图
∟
G
H
解题关键点
过点F作FH⊥CD于点H,交AB于点G,证FG是△ABE的中位线.
请完成精练本习题
同课章节目录
