数学人教A版(2019)必修第一册5.2.2同角三角函数的基本关系 课件(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.2.2同角三角函数的基本关系 课件(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 724.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 18:51:06 | ||
图片预览










文档简介
(共30张PPT)
§5.2.2 同角三角函数的基本关系
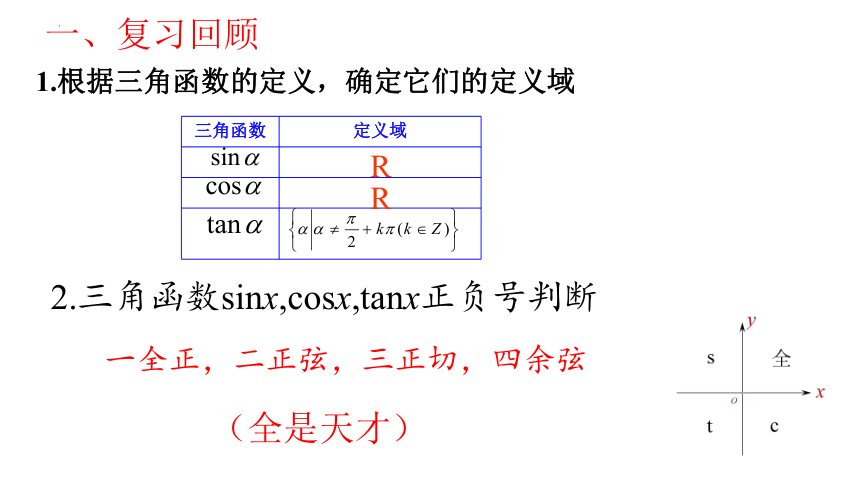
1.根据三角函数的定义,确定它们的定义域
三角函数 定义域
R
R
一全正,二正弦,三正切,四余弦
2.三角函数sinx,cosx,tanx正负号判断
(全是天才)
一、复习回顾
角α 00 900 1800 2700 3600
角α的弧度数
sinα
cosα
tanα
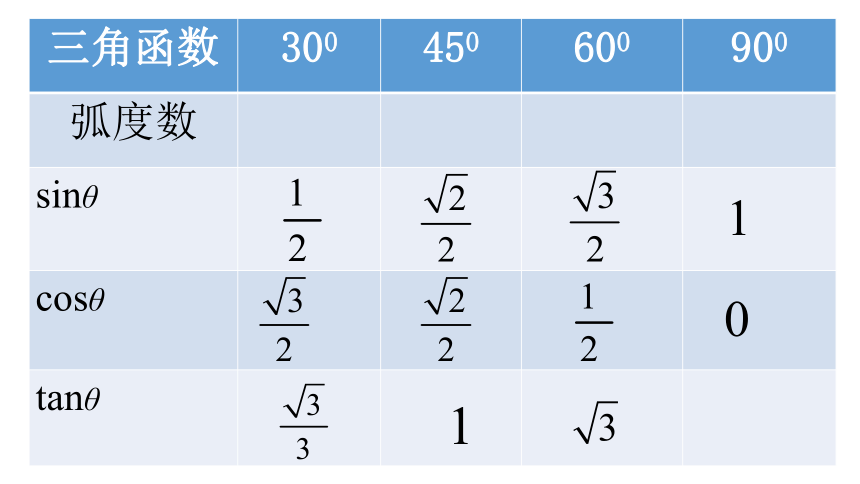
3.特殊角的三角函数值
三角函数 300 450 600 900
弧度数
sinθ
cosθ
tanθ
平方关系:
商数关系:
同一个角的正弦、余弦的平方和等于1
同一个角的正弦、余弦的商等于角的正切
二、同角三角函数的基本关系
思考:对于平方关系 可作哪些变形?
思考:对于商数关系 可作哪些变形?
概念辨析:
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
三、例题解析
从而
解:因为 , 所以 是第三或第四象限角.
由 得
如果 是第三象限角,那么
如果 是第四象限角,那么
分类讨论:符号看象限!
知一求二
探究点一 sin α,cos α,tan α知一求二
(2)已知tan α=-2,求cos α,sin α.
探究点二 已知正切值求值
(3)4sin2α-3sin αcos α-5cos2α.
即时训练2-1:已知tan α=3,求下列各式的值.
(3)cos2α-3sin αcos α.
方法总结
已知角α的正切值,求由sin α和cos α构成的代数式的值,构成的代数式通常是分式齐次式或整式齐次式.
探究点三 三角函数式的证明
sin α+cos α,sin α-cos α,sin αcos α之间的关系
1.(sin α±cos α)2=1±2sin αcos α.
2.(sin α+cos α)2+(sin α-cos α)2=2.
探究点四 同角三角函数的基本关系的综合应用
反思感悟
1.关于sin α,cos α的齐次式,可以通过分子、分母同除以cos α或cos2α转化为关于tan α的式子后再求值.
2.已知正切值求形如sin αcos α,2sin2α-3cos2α等的值,代数式中不含分母,可以视分母为1,灵活地进行“1”的代换.即先将1=sin2α+cos2α代换后,再同除以cos2α,构造出关于tan α的代数式.
课堂达标
A
D
3.化简(1+tan2α)·cos2α= .
答案:1
§5.2.2 同角三角函数的基本关系
1.根据三角函数的定义,确定它们的定义域
三角函数 定义域
R
R
一全正,二正弦,三正切,四余弦
2.三角函数sinx,cosx,tanx正负号判断
(全是天才)
一、复习回顾
角α 00 900 1800 2700 3600
角α的弧度数
sinα
cosα
tanα
3.特殊角的三角函数值
三角函数 300 450 600 900
弧度数
sinθ
cosθ
tanθ
平方关系:
商数关系:
同一个角的正弦、余弦的平方和等于1
同一个角的正弦、余弦的商等于角的正切
二、同角三角函数的基本关系
思考:对于平方关系 可作哪些变形?
思考:对于商数关系 可作哪些变形?
概念辨析:
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
三、例题解析
从而
解:因为 , 所以 是第三或第四象限角.
由 得
如果 是第三象限角,那么
如果 是第四象限角,那么
分类讨论:符号看象限!
知一求二
探究点一 sin α,cos α,tan α知一求二
(2)已知tan α=-2,求cos α,sin α.
探究点二 已知正切值求值
(3)4sin2α-3sin αcos α-5cos2α.
即时训练2-1:已知tan α=3,求下列各式的值.
(3)cos2α-3sin αcos α.
方法总结
已知角α的正切值,求由sin α和cos α构成的代数式的值,构成的代数式通常是分式齐次式或整式齐次式.
探究点三 三角函数式的证明
sin α+cos α,sin α-cos α,sin αcos α之间的关系
1.(sin α±cos α)2=1±2sin αcos α.
2.(sin α+cos α)2+(sin α-cos α)2=2.
探究点四 同角三角函数的基本关系的综合应用
反思感悟
1.关于sin α,cos α的齐次式,可以通过分子、分母同除以cos α或cos2α转化为关于tan α的式子后再求值.
2.已知正切值求形如sin αcos α,2sin2α-3cos2α等的值,代数式中不含分母,可以视分母为1,灵活地进行“1”的代换.即先将1=sin2α+cos2α代换后,再同除以cos2α,构造出关于tan α的代数式.
课堂达标
A
D
3.化简(1+tan2α)·cos2α= .
答案:1
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
