数学人教A版(2019)必修第二册6.1平面向量的概念 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册6.1平面向量的概念 课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 491.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 18:52:16 | ||
图片预览




文档简介
(共20张PPT)
6.1 平面向量的概念
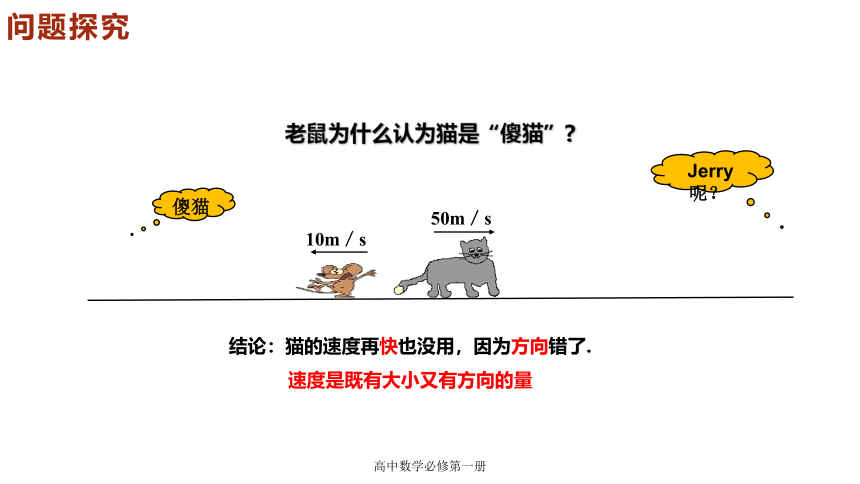
老鼠为什么认为猫是“傻猫”
结论:猫的速度再快也没用,因为方向错了.
速度是既有大小又有方向的量
50m/s
傻猫
10m/s
Jerry呢?
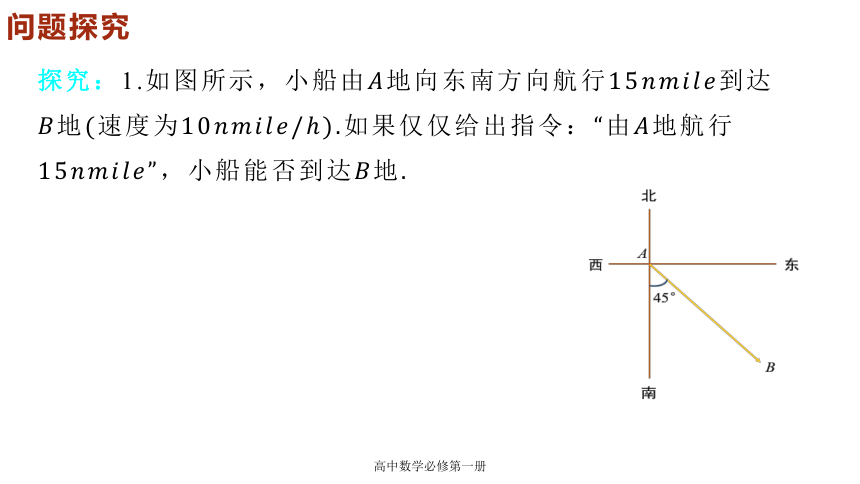
探究:1.如图所示,小船由地向东南方向航行到达地(速度为如果仅仅给出指令:“由地航行”,小船能否到达地.
探究:2.我们从一支笔、一棵树、一本书中抽象出只有大小的数量“1”.类似地,我们可以对“位移”“速度”进行抽象,它们的共同特征是什么?
探究:2.你还能举出具有这种特征的量吗?
1.向量的概念
(1)向量:在数学中,我们把既有大小又有方向的量叫做向量.
(2)数量:只有大小没有方向的量叫做数量.
矢量
标量
探究:3.我们知道数量可以用实数表示,而实数与数轴上的点一一对应,所以数量可以用数轴上的点表示,那么我们用什么表示这样既有大小又有方向的量呢?
A
(起点)
(终点)
B
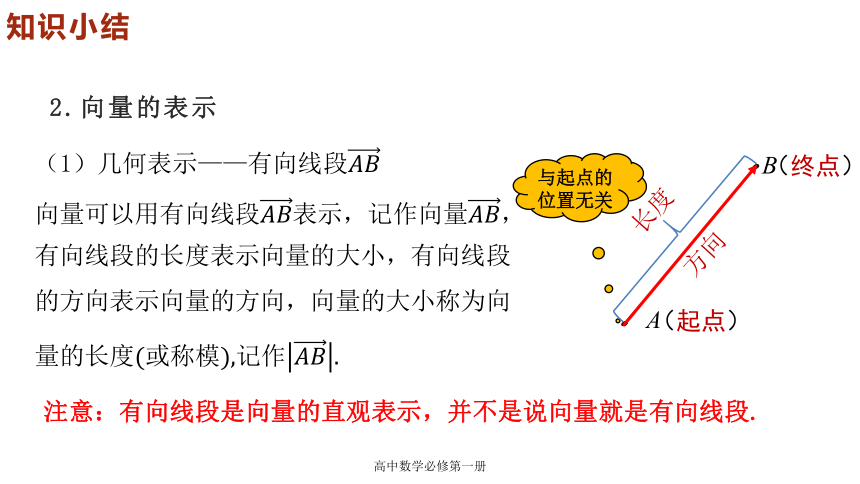
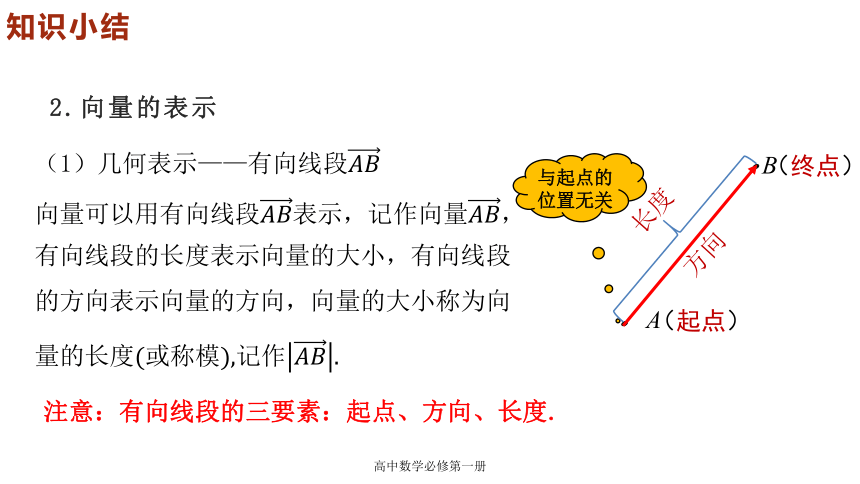
2.向量的表示
(1)几何表示——有向线段
向量可以用有向线段表示,记作向量,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向,向量的大小称为向量的长度(或称模),记作
与起点的位置无关
A
方向
(起点)
(终点)
B
长度
注意:有向线段是向量的直观表示,并不是说向量就是有向线段.
2.向量的表示
(1)几何表示——有向线段
向量可以用有向线段表示,记作向量,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向,向量的大小称为向量的长度(或称模),记作
与起点的位置无关
A
方向
(起点)
(终点)
B
长度
注意:有向线段的三要素:起点、方向、长度.
2.向量的表示
(1)几何表示——有向线段
向量可以用有向线段表示,记作向量,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向,向量的大小称为向量的长度(或称模),记作
与起点的位置无关
A
方向
(起点)
(终点)
B
长度
注意:向量不能比较大小,向量的模可以比较大小.
2.向量的表示
(1)字母表示——向量可以用字母表示(印刷时黑体表示).
手写时用.
注意:手写向量时要带箭头.
例1 某人从点出发向东走了5米到达点,然后改变方向按东北方向走了10米到达点,到达点后又改变方向向西走了10米到达点.
(1)作出向量,,;
例1 某人从点出发向东走了5米到达点,然后改变方向按东北方向走了10米到达点,到达点后又改变方向向西走了10米到达点.
(2)求的模;
长度
3.两个特殊向量
(1)零向量——
长度:长度为0的向量;
方向:方向为任意的向量.
(2)单位向量
长度:长度为1的向量;
方向:方向不确定的向量.
1个
无数个
例2 (1)(多选)下列说法错误的是( )
A.数量可以比较大小,向量也可以比较大小
B.方向不同的向量不能比较大小,但同向的可以比较大小
C.向量的大小与方向有关
D.向量的模可以比较大小
ABC
向量不能比较大小
向量的大小即向量的模即长度
向量的模是数量
例2 (2)给出下列说法:
①零向量是没有方向的;
②零向量的长度为0;
③零向量的方向是任意的;
④单位向量都相等.
其中正确的是_______.(填序号)
②③
零向量方向任意,不是没有
单位向量方向
不一定相同
4.向量间的两种特殊关系
(1)平行(共线)向量——
长度:非零;
方向:相同或相反.
(2)相等向量——
长度:长度相等;
方向:方向相同.
注意:零向量与任意向量平行.
例4 如图所示,的三边均不相等,分别是的中点.
(1)写出与共线的向量;
例4 如图所示,的三边均不相等,分别是的中点.
(2)写出模与的模相等的向量;
(3)写出与相等的向量.
例4 如图所示,设是正六边形的中心.
(1)写出图中的共线向量;
(2)分别写出图中与相等的向量.
6.1 平面向量的概念
老鼠为什么认为猫是“傻猫”
结论:猫的速度再快也没用,因为方向错了.
速度是既有大小又有方向的量
50m/s
傻猫
10m/s
Jerry呢?
探究:1.如图所示,小船由地向东南方向航行到达地(速度为如果仅仅给出指令:“由地航行”,小船能否到达地.
探究:2.我们从一支笔、一棵树、一本书中抽象出只有大小的数量“1”.类似地,我们可以对“位移”“速度”进行抽象,它们的共同特征是什么?
探究:2.你还能举出具有这种特征的量吗?
1.向量的概念
(1)向量:在数学中,我们把既有大小又有方向的量叫做向量.
(2)数量:只有大小没有方向的量叫做数量.
矢量
标量
探究:3.我们知道数量可以用实数表示,而实数与数轴上的点一一对应,所以数量可以用数轴上的点表示,那么我们用什么表示这样既有大小又有方向的量呢?
A
(起点)
(终点)
B
2.向量的表示
(1)几何表示——有向线段
向量可以用有向线段表示,记作向量,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向,向量的大小称为向量的长度(或称模),记作
与起点的位置无关
A
方向
(起点)
(终点)
B
长度
注意:有向线段是向量的直观表示,并不是说向量就是有向线段.
2.向量的表示
(1)几何表示——有向线段
向量可以用有向线段表示,记作向量,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向,向量的大小称为向量的长度(或称模),记作
与起点的位置无关
A
方向
(起点)
(终点)
B
长度
注意:有向线段的三要素:起点、方向、长度.
2.向量的表示
(1)几何表示——有向线段
向量可以用有向线段表示,记作向量,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向,向量的大小称为向量的长度(或称模),记作
与起点的位置无关
A
方向
(起点)
(终点)
B
长度
注意:向量不能比较大小,向量的模可以比较大小.
2.向量的表示
(1)字母表示——向量可以用字母表示(印刷时黑体表示).
手写时用.
注意:手写向量时要带箭头.
例1 某人从点出发向东走了5米到达点,然后改变方向按东北方向走了10米到达点,到达点后又改变方向向西走了10米到达点.
(1)作出向量,,;
例1 某人从点出发向东走了5米到达点,然后改变方向按东北方向走了10米到达点,到达点后又改变方向向西走了10米到达点.
(2)求的模;
长度
3.两个特殊向量
(1)零向量——
长度:长度为0的向量;
方向:方向为任意的向量.
(2)单位向量
长度:长度为1的向量;
方向:方向不确定的向量.
1个
无数个
例2 (1)(多选)下列说法错误的是( )
A.数量可以比较大小,向量也可以比较大小
B.方向不同的向量不能比较大小,但同向的可以比较大小
C.向量的大小与方向有关
D.向量的模可以比较大小
ABC
向量不能比较大小
向量的大小即向量的模即长度
向量的模是数量
例2 (2)给出下列说法:
①零向量是没有方向的;
②零向量的长度为0;
③零向量的方向是任意的;
④单位向量都相等.
其中正确的是_______.(填序号)
②③
零向量方向任意,不是没有
单位向量方向
不一定相同
4.向量间的两种特殊关系
(1)平行(共线)向量——
长度:非零;
方向:相同或相反.
(2)相等向量——
长度:长度相等;
方向:方向相同.
注意:零向量与任意向量平行.
例4 如图所示,的三边均不相等,分别是的中点.
(1)写出与共线的向量;
例4 如图所示,的三边均不相等,分别是的中点.
(2)写出模与的模相等的向量;
(3)写出与相等的向量.
例4 如图所示,设是正六边形的中心.
(1)写出图中的共线向量;
(2)分别写出图中与相等的向量.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
