第六章 反比例函数期末章节拔高练习(含答案)
文档属性
| 名称 | 第六章 反比例函数期末章节拔高练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 658.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 04:07:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版数学九年级上册第六章反比例函数期末章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,函数的图象经过斜边OB的中点C,连结AC.如果,那么的周长为( ).
A. B. C. D.
2.已知点在函数的图象上,则m的值是( )
A.-3 B.-12 C.1· D.-1
3.如果等腰三角形的底边长为x,底边上的高为y,则它的面积为定值S时,x与y的函数关系为( )
A. B. C. D.
4.已知点(-2,),(3,)是反比例函数图象上的两点,则有( )
A. B. C. D.
5.如图所示,在平面直角坐标系中y=﹣(x<0)与直线y=﹣x﹣3的图象交于点A(m,n),则的值为( )
A.﹣3 B.﹣1 C.3 D.1
6.下列函数是反比例函数的是( )
A.y=-1 B.y= C.y= D.y=
7.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系.
B.菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系.
C.一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的密度之间的关系.
D.压力为600N时,压强p与受力面积S之间的关系.
8.(2016广西钦州市)已知点A(,)、B(,)是反比例函数图象上的两点,若<0<,则有( )
A. B. C. D.
9.如图,函数和函数的图象相交于点,.若,则的取值范围是( )
A.或 B.或
C.或 D.或
10.如图,已知是反比例函数的图象上的一个动点,是轴上的一个动点,且,当点在图象上自左向右运动过程中,的面积变化情况是( )
A.逐渐增大 B.逐渐减小 C.不变 D.以上都不是
二、填空题
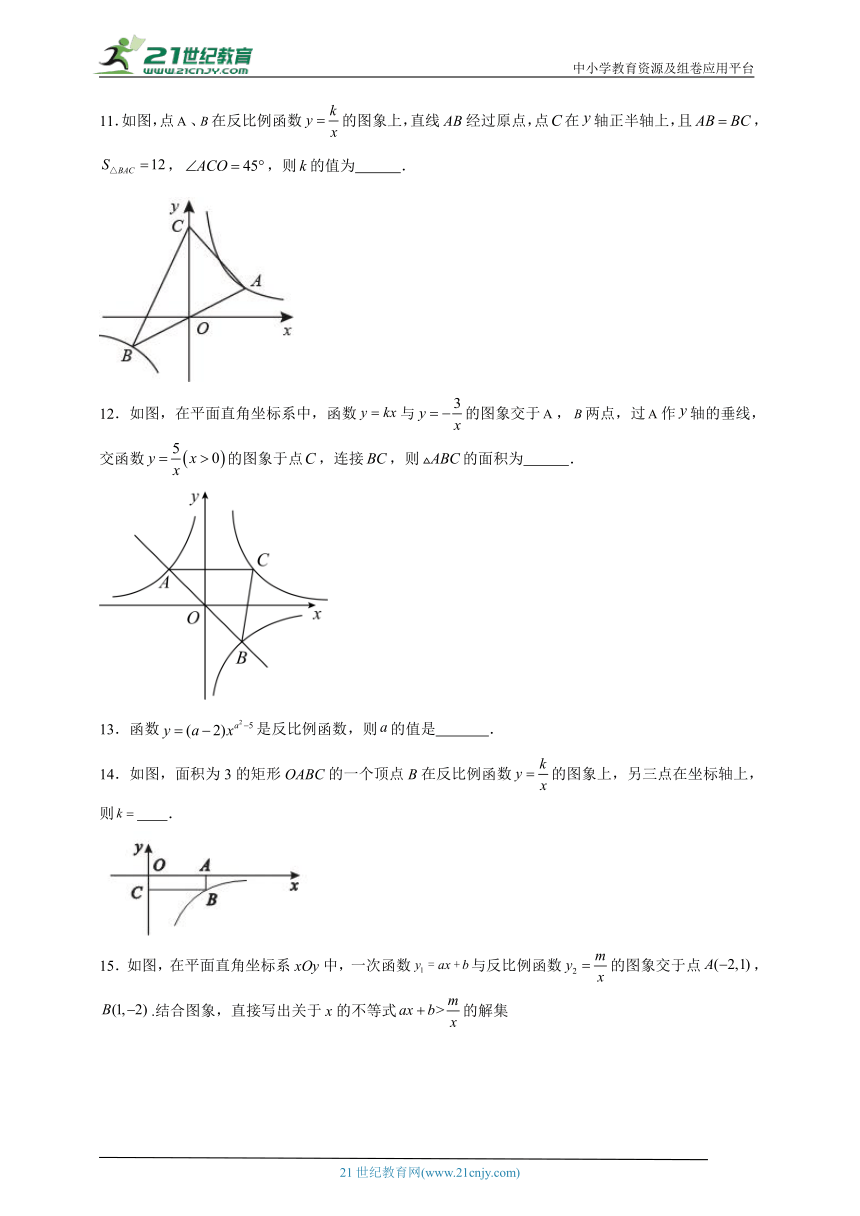
11.如图,点、在反比例函数的图象上,直线经过原点,点在轴正半轴上,且,,,则的值为 .
12.如图,在平面直角坐标系中,函数与的图象交于,两点,过作轴的垂线,交函数的图象于点,连接,则的面积为 .
13.函数是反比例函数,则的值是 .
14.如图,面积为3的矩形OABC的一个顶点B在反比例函数的图象上,另三点在坐标轴上,则 .
15.如图,在平面直角坐标系xOy中,一次函数与反比例函数的图象交于点,.结合图象,直接写出关于x的不等式的解集
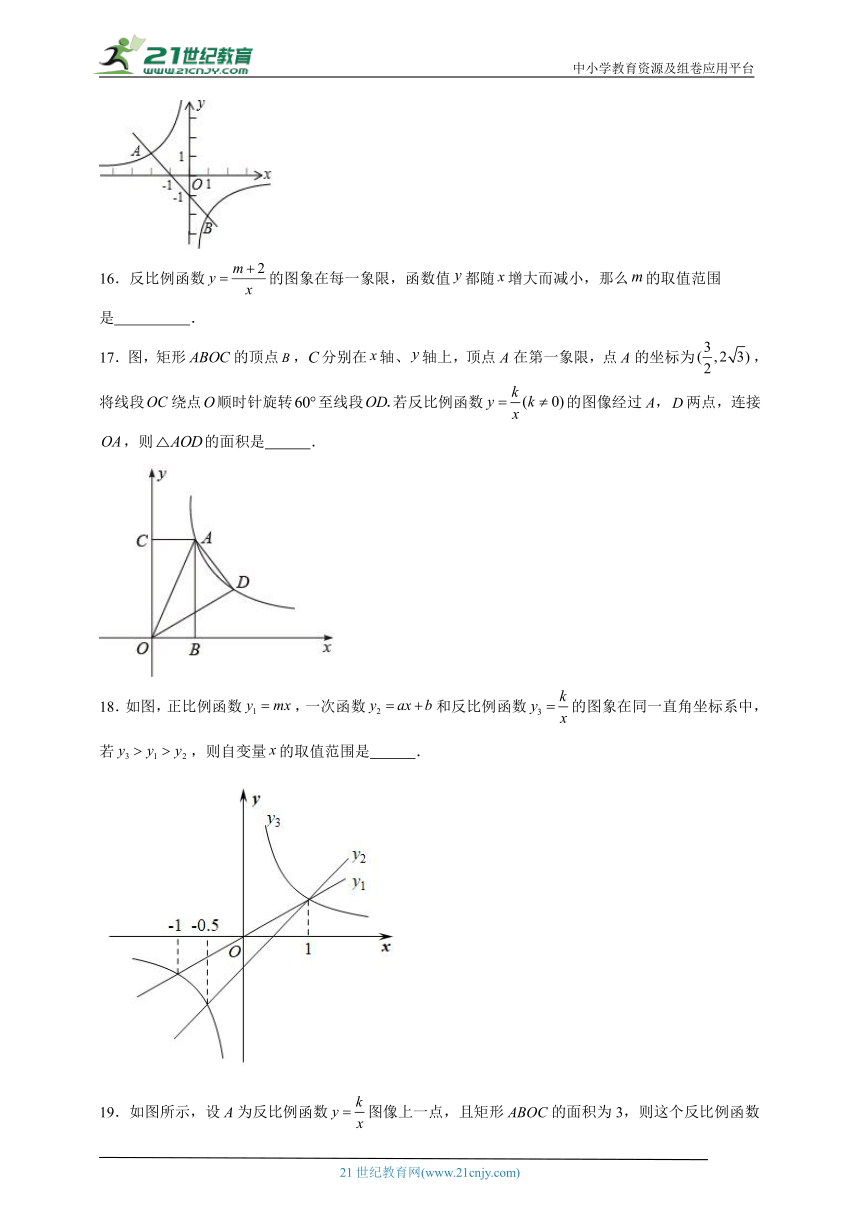
16.反比例函数的图象在每一象限,函数值都随增大而减小,那么的取值范围是 .
17.图,矩形的顶点,分别在轴、轴上,顶点A在第一象限,点A的坐标为,将线段绕点顺时针旋转至线段若反比例函数的图像经过A,两点,连接,则的面积是 .
18.如图,正比例函数,一次函数和反比例函数的图象在同一直角坐标系中,若,则自变量的取值范围是 .
19.如图所示,设A为反比例函数图像上一点,且矩形ABOC的面积为3,则这个反比例函数解析式为 .
20.如图,点A的坐标为(2,0),点B的坐标为(0,4),点C在反比例函数y= k>0,x>0)的图象上,AC⊥AB,过点C作CD∥AB,交反比例函数于点D,且CD=2AB,则k的值为 .
三、解答题
21.某农业大学计划修建一块面积为的矩形试验田.
(1)试验田的长y(单位:m)关于宽x(单位:m)的函数解析式是什么?
(2)如果试验田的长与宽的比为,那么试验田的长与宽分别为多少?
22.如图,一次函数的图象与反比例函数的图象交于点两点.
(1)求一次函数与反比例函数的解析式;
(2)求的面积;
23.为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
24.如图,在平面直角坐标系中,为坐标原点,的边垂直于轴、垂足为点,反比例函数的图象经过的中点、且与相交于点.经过、两点的一次函数解析式为,若点的坐标为,.且.
(1)求反比例函数的解析式;
(2)在直线上有一点,的面积等于.求满足条件的点的坐标;
(3)请观察图象直接写出不等式的解集.
25.如图,一次函数的图象与坐标轴相交于点A(,0)和点B,与反比例函数相交于点C(2,m).
(1)求出一次函数与反比例函数的解析式;
(2)若点是反比例函数图象上的一点,连接并延长,交轴正半轴于点,若时,
①求出直线的表达式;
②求出的面积.
参考答案:
1.D
2.A
3.C
4.A
5.D
6.C
7.C
8.D
9.A
10.C
11.4.
12.8.
13.
14.-3
15.x<-2或016.m>-2
17./
18.或
19.
20.
21.(1);(2),
22.(1),;(2)8
23.(1)y=2x;(2)y=;(3)此次消毒有效时间为16﹣1=15分钟.
24.(1)y1=;(2)P(2,4)或(﹣14,﹣4);(3)x<﹣4或﹣2<x<0.
25.(1)一次函数为,反比例函数为
(2)①直线的解析式为;②16
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版数学九年级上册第六章反比例函数期末章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,函数的图象经过斜边OB的中点C,连结AC.如果,那么的周长为( ).
A. B. C. D.
2.已知点在函数的图象上,则m的值是( )
A.-3 B.-12 C.1· D.-1
3.如果等腰三角形的底边长为x,底边上的高为y,则它的面积为定值S时,x与y的函数关系为( )
A. B. C. D.
4.已知点(-2,),(3,)是反比例函数图象上的两点,则有( )
A. B. C. D.
5.如图所示,在平面直角坐标系中y=﹣(x<0)与直线y=﹣x﹣3的图象交于点A(m,n),则的值为( )
A.﹣3 B.﹣1 C.3 D.1
6.下列函数是反比例函数的是( )
A.y=-1 B.y= C.y= D.y=
7.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系.
B.菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系.
C.一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的密度之间的关系.
D.压力为600N时,压强p与受力面积S之间的关系.
8.(2016广西钦州市)已知点A(,)、B(,)是反比例函数图象上的两点,若<0<,则有( )
A. B. C. D.
9.如图,函数和函数的图象相交于点,.若,则的取值范围是( )
A.或 B.或
C.或 D.或
10.如图,已知是反比例函数的图象上的一个动点,是轴上的一个动点,且,当点在图象上自左向右运动过程中,的面积变化情况是( )
A.逐渐增大 B.逐渐减小 C.不变 D.以上都不是
二、填空题
11.如图,点、在反比例函数的图象上,直线经过原点,点在轴正半轴上,且,,,则的值为 .
12.如图,在平面直角坐标系中,函数与的图象交于,两点,过作轴的垂线,交函数的图象于点,连接,则的面积为 .
13.函数是反比例函数,则的值是 .
14.如图,面积为3的矩形OABC的一个顶点B在反比例函数的图象上,另三点在坐标轴上,则 .
15.如图,在平面直角坐标系xOy中,一次函数与反比例函数的图象交于点,.结合图象,直接写出关于x的不等式的解集
16.反比例函数的图象在每一象限,函数值都随增大而减小,那么的取值范围是 .
17.图,矩形的顶点,分别在轴、轴上,顶点A在第一象限,点A的坐标为,将线段绕点顺时针旋转至线段若反比例函数的图像经过A,两点,连接,则的面积是 .
18.如图,正比例函数,一次函数和反比例函数的图象在同一直角坐标系中,若,则自变量的取值范围是 .
19.如图所示,设A为反比例函数图像上一点,且矩形ABOC的面积为3,则这个反比例函数解析式为 .
20.如图,点A的坐标为(2,0),点B的坐标为(0,4),点C在反比例函数y= k>0,x>0)的图象上,AC⊥AB,过点C作CD∥AB,交反比例函数于点D,且CD=2AB,则k的值为 .
三、解答题
21.某农业大学计划修建一块面积为的矩形试验田.
(1)试验田的长y(单位:m)关于宽x(单位:m)的函数解析式是什么?
(2)如果试验田的长与宽的比为,那么试验田的长与宽分别为多少?
22.如图,一次函数的图象与反比例函数的图象交于点两点.
(1)求一次函数与反比例函数的解析式;
(2)求的面积;
23.为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
24.如图,在平面直角坐标系中,为坐标原点,的边垂直于轴、垂足为点,反比例函数的图象经过的中点、且与相交于点.经过、两点的一次函数解析式为,若点的坐标为,.且.
(1)求反比例函数的解析式;
(2)在直线上有一点,的面积等于.求满足条件的点的坐标;
(3)请观察图象直接写出不等式的解集.
25.如图,一次函数的图象与坐标轴相交于点A(,0)和点B,与反比例函数相交于点C(2,m).
(1)求出一次函数与反比例函数的解析式;
(2)若点是反比例函数图象上的一点,连接并延长,交轴正半轴于点,若时,
①求出直线的表达式;
②求出的面积.
参考答案:
1.D
2.A
3.C
4.A
5.D
6.C
7.C
8.D
9.A
10.C
11.4.
12.8.
13.
14.-3
15.x<-2或0
17./
18.或
19.
20.
21.(1);(2),
22.(1),;(2)8
23.(1)y=2x;(2)y=;(3)此次消毒有效时间为16﹣1=15分钟.
24.(1)y1=;(2)P(2,4)或(﹣14,﹣4);(3)x<﹣4或﹣2<x<0.
25.(1)一次函数为,反比例函数为
(2)①直线的解析式为;②16
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
