第六章 反比例函数期末章节基础练习(含答案)
文档属性
| 名称 | 第六章 反比例函数期末章节基础练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 622.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版数学九年级上册第六章反比例函数期末章节基础练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如果点A(-2,y1),B(2,y2),C(-3,y3)都在反比例函数y=的图象上,那么y1,y2,y3的大小关系正确的是( )
A.y12.反比例函数y=中,当x>0时,y随x的增大而增大,则m的取值范围是( )
A.m> B.m<2 C.m< D.m>2
3.在同一平面直角坐标系中,函数y=kx与y=的图象大致是( )
A.(1)(3) B.(1)(4) C.(2)(3) D.(2)(4)
4.已知反比例函数的图象在第一、第三象限内,设函数图象上有两点、,若,则与的大小关系是( )
A. B. C. D.不能确定
5.如图,直线与双曲线交于、两点,过点作轴,垂足为,连接,若,则的值是( )
A.2 B.4 C.-2 D.-4
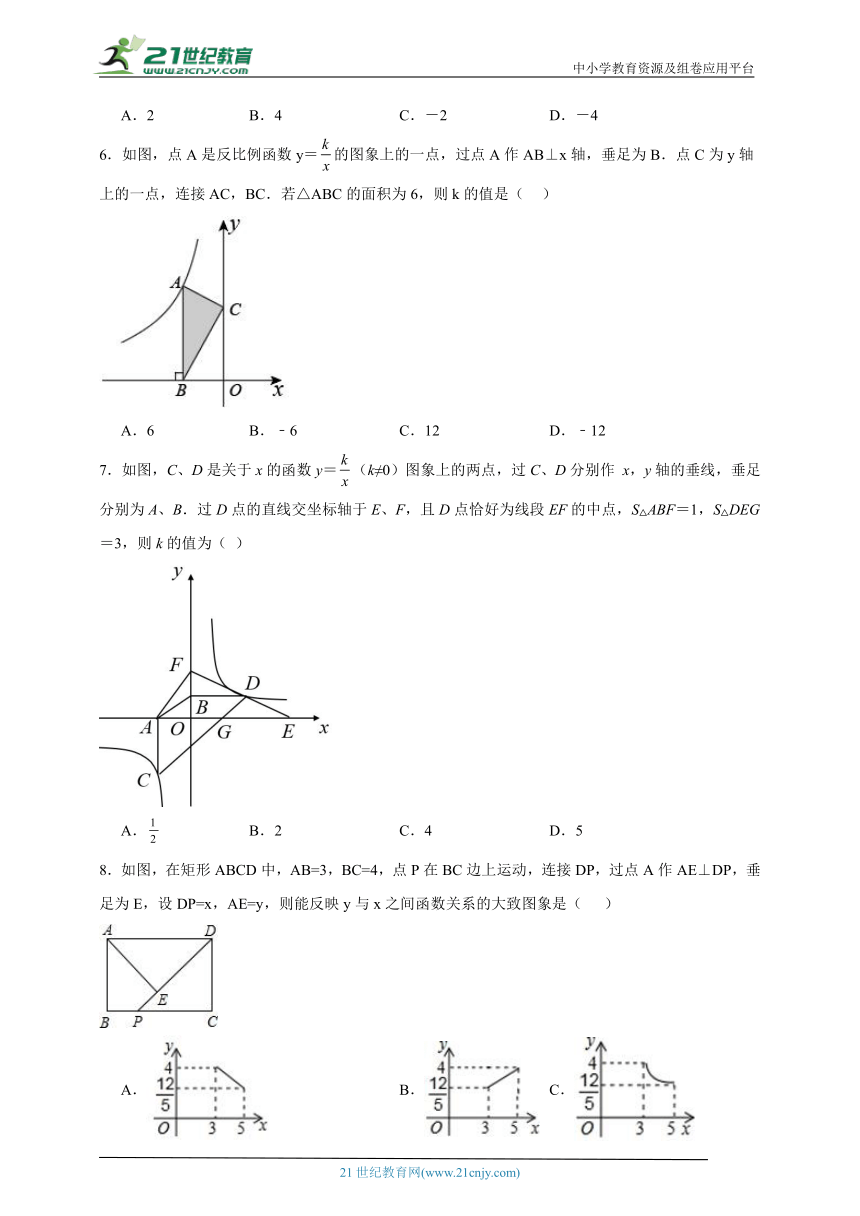
6.如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为6,则k的值是( )
A.6 B.﹣6 C.12 D.﹣12
7.如图,C、D是关于x的函数y=(k≠0)图象上的两点,过C、D分别作 x,y轴的垂线,垂足分别为A、B.过D点的直线交坐标轴于E、F,且D点恰好为线段EF的中点,S△ABF=1,S△DEG=3,则k的值为( )
A. B.2 C.4 D.5
8.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )
A. B. C. D.
9.下列说法正确的个数是( )①是的函数;②等腰三角形面积一定,它的底边和底边上的高成正比例;③在函数中,随的增大而减小;④已知,则直线经过第二,四象限.
A.1个 B.2个 C.3个 D.4个
10.已知点,,在函数(k为常数)的图像上,则下列判断正确的是( )
A. B. C. D.
二、填空题
11.已知三点(a,m)、(b,n)和(c,t)在反比例函数y=(k>0)的图像上,若a<0<b<c,则m、n和t的大小关系是 .(用“<”连接)
12.如图,点A在双曲线y=上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若平行四边形ABCD面积为4,则反比例函数y=的关系式为 .
13.如图,点M是反比例函数的图象上一点,过M点作x轴、y轴的平行线,若,则此反比例函数解析式为 .
14.若函数y=x﹣1与的图象的交点坐标为(m,n),则的值为 .
15.已知一次函数的图像与反比例函数的图像交于点,当时,对应的的取值范围是 .
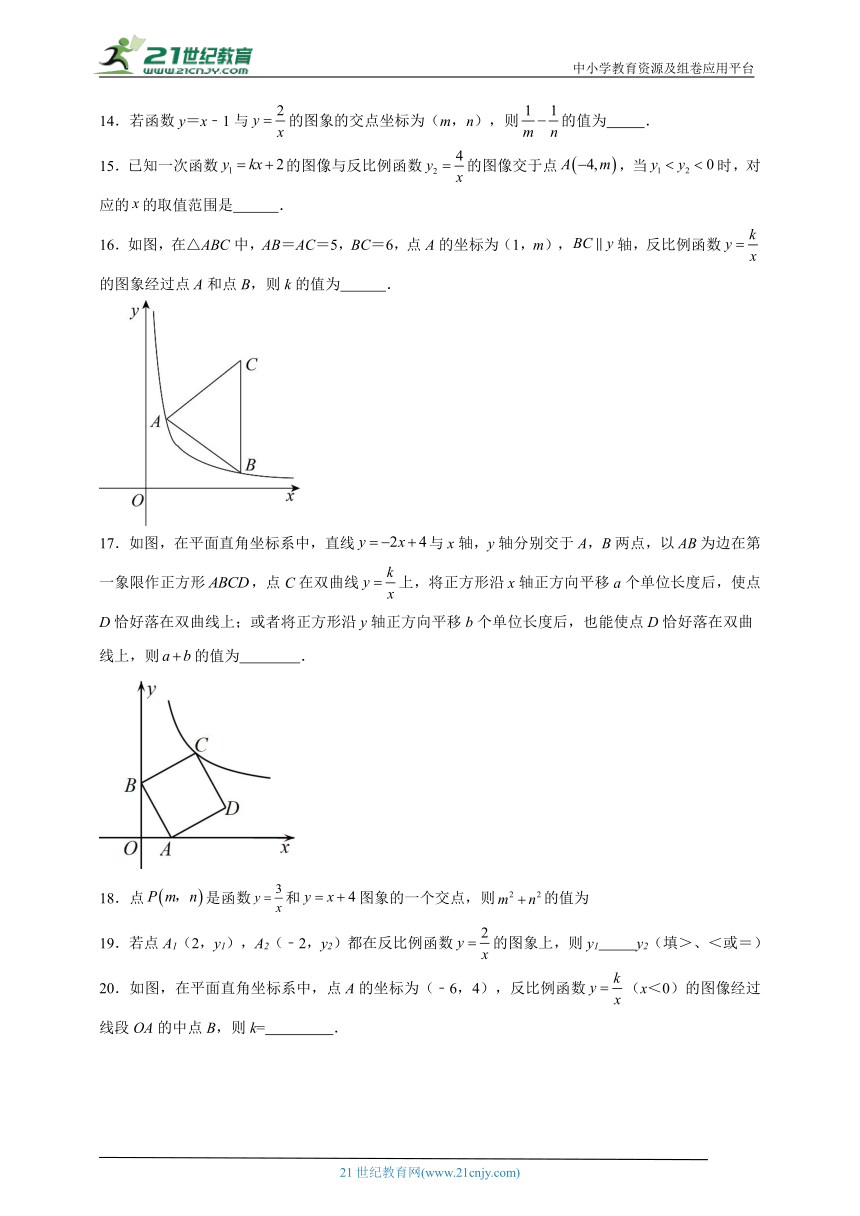
16.如图,在△ABC中,AB=AC=5,BC=6,点A的坐标为(1,m),轴,反比例函数的图象经过点A和点B,则k的值为 .
17.如图,在平面直角坐标系中,直线与x轴,y轴分别交于A,B两点,以为边在第一象限作正方形,点C在双曲线上,将正方形沿x轴正方向平移a个单位长度后,使点D恰好落在双曲线上;或者将正方形沿y轴正方向平移b个单位长度后,也能使点D恰好落在双曲线上,则的值为 .
18.点是函数和图象的一个交点,则的值为
19.若点A1(2,y1),A2(﹣2,y2)都在反比例函数的图象上,则y1 y2(填>、<或=)
20.如图,在平面直角坐标系中,点A的坐标为(﹣6,4),反比例函数(x<0)的图像经过线段OA的中点B,则k= .
三、解答题
21.如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为,C坐标为,双曲线上经过点C,直线CD:在经过点C交y轴于点D,与双曲线的另一分支相交于点.
(1)分别求双曲线和直线的函数关系式;
(2)判断点B是否在双曲线上;
(3)当时,直接写出x的取值范围.
22.如图,一次函数y=kx+b(k≠0)与反比例函数y=(a≠0)的图象在第一象限交于A、B两点,A点的坐标为(m,4),B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C.若OC=CA,
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在直线BD上是否存在一点E,使得△AOE是以AO为直角边的直角三角形,直接写出所有可能的E点坐标.
23.电流I、电阻R、电功率P之间满足关系式.已知,填写下表并回答问题.
1 2 3 4 5 6 7 8
(1)变量R是变量I的函数吗?
(2)变量R是变量I的反比例函数吗?
24.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB.BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:
(1)求线段AB和双曲线CD的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
25.如图1,点M,N在反比例函数的图象上,过点M作轴,过点N作轴,垂足分别为E,F.
(1)探究发现:
①若,则的面积为 ___________,的面积为 ___________;
②若,则的面积为 ___________,的面积为 ___________.
(2)猜想验证:
①如图1,试判断与的位置关系为 ___________;
②如图2,题中的其他条件不变,只改变点M,N的位置,请判断与的位置关系,并说明理由.
(3)推广应用:
在同一坐标系中,反比例函数与的图象上如图3所示,B,C是反比例函数的图象上的两点,过点B作x轴的平行线与的图象相交于点D,过点C作y轴的平行线的图象相交于点E,与相交于点,请求出的值.
参考答案:
1.A
2.A
3.B
4.D
5.A
6.D
7.C
8.C
9.A
10.A
11.
12.
13.
14.
15.
16.
17.8
18.
19.>
20.-6
21.(1),
(2)点B在双曲线上
(3)或
22.(1)y=,y=x+6;(2);(3)(,2)或(,2).
23.略,(1)R是I的函数;(2)R不是I的反比例函数
24.(1),
(2)20°C
(3)恒温系统最多关闭10小时,蔬菜才能避免受到伤害
25.(1)①1,1,②,
(2)①,②
(3)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版数学九年级上册第六章反比例函数期末章节基础练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如果点A(-2,y1),B(2,y2),C(-3,y3)都在反比例函数y=的图象上,那么y1,y2,y3的大小关系正确的是( )
A.y1
A.m> B.m<2 C.m< D.m>2
3.在同一平面直角坐标系中,函数y=kx与y=的图象大致是( )
A.(1)(3) B.(1)(4) C.(2)(3) D.(2)(4)
4.已知反比例函数的图象在第一、第三象限内,设函数图象上有两点、,若,则与的大小关系是( )
A. B. C. D.不能确定
5.如图,直线与双曲线交于、两点,过点作轴,垂足为,连接,若,则的值是( )
A.2 B.4 C.-2 D.-4
6.如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为6,则k的值是( )
A.6 B.﹣6 C.12 D.﹣12
7.如图,C、D是关于x的函数y=(k≠0)图象上的两点,过C、D分别作 x,y轴的垂线,垂足分别为A、B.过D点的直线交坐标轴于E、F,且D点恰好为线段EF的中点,S△ABF=1,S△DEG=3,则k的值为( )
A. B.2 C.4 D.5
8.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )
A. B. C. D.
9.下列说法正确的个数是( )①是的函数;②等腰三角形面积一定,它的底边和底边上的高成正比例;③在函数中,随的增大而减小;④已知,则直线经过第二,四象限.
A.1个 B.2个 C.3个 D.4个
10.已知点,,在函数(k为常数)的图像上,则下列判断正确的是( )
A. B. C. D.
二、填空题
11.已知三点(a,m)、(b,n)和(c,t)在反比例函数y=(k>0)的图像上,若a<0<b<c,则m、n和t的大小关系是 .(用“<”连接)
12.如图,点A在双曲线y=上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若平行四边形ABCD面积为4,则反比例函数y=的关系式为 .
13.如图,点M是反比例函数的图象上一点,过M点作x轴、y轴的平行线,若,则此反比例函数解析式为 .
14.若函数y=x﹣1与的图象的交点坐标为(m,n),则的值为 .
15.已知一次函数的图像与反比例函数的图像交于点,当时,对应的的取值范围是 .
16.如图,在△ABC中,AB=AC=5,BC=6,点A的坐标为(1,m),轴,反比例函数的图象经过点A和点B,则k的值为 .
17.如图,在平面直角坐标系中,直线与x轴,y轴分别交于A,B两点,以为边在第一象限作正方形,点C在双曲线上,将正方形沿x轴正方向平移a个单位长度后,使点D恰好落在双曲线上;或者将正方形沿y轴正方向平移b个单位长度后,也能使点D恰好落在双曲线上,则的值为 .
18.点是函数和图象的一个交点,则的值为
19.若点A1(2,y1),A2(﹣2,y2)都在反比例函数的图象上,则y1 y2(填>、<或=)
20.如图,在平面直角坐标系中,点A的坐标为(﹣6,4),反比例函数(x<0)的图像经过线段OA的中点B,则k= .
三、解答题
21.如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为,C坐标为,双曲线上经过点C,直线CD:在经过点C交y轴于点D,与双曲线的另一分支相交于点.
(1)分别求双曲线和直线的函数关系式;
(2)判断点B是否在双曲线上;
(3)当时,直接写出x的取值范围.
22.如图,一次函数y=kx+b(k≠0)与反比例函数y=(a≠0)的图象在第一象限交于A、B两点,A点的坐标为(m,4),B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C.若OC=CA,
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在直线BD上是否存在一点E,使得△AOE是以AO为直角边的直角三角形,直接写出所有可能的E点坐标.
23.电流I、电阻R、电功率P之间满足关系式.已知,填写下表并回答问题.
1 2 3 4 5 6 7 8
(1)变量R是变量I的函数吗?
(2)变量R是变量I的反比例函数吗?
24.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB.BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:
(1)求线段AB和双曲线CD的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
25.如图1,点M,N在反比例函数的图象上,过点M作轴,过点N作轴,垂足分别为E,F.
(1)探究发现:
①若,则的面积为 ___________,的面积为 ___________;
②若,则的面积为 ___________,的面积为 ___________.
(2)猜想验证:
①如图1,试判断与的位置关系为 ___________;
②如图2,题中的其他条件不变,只改变点M,N的位置,请判断与的位置关系,并说明理由.
(3)推广应用:
在同一坐标系中,反比例函数与的图象上如图3所示,B,C是反比例函数的图象上的两点,过点B作x轴的平行线与的图象相交于点D,过点C作y轴的平行线的图象相交于点E,与相交于点,请求出的值.
参考答案:
1.A
2.A
3.B
4.D
5.A
6.D
7.C
8.C
9.A
10.A
11.
12.
13.
14.
15.
16.
17.8
18.
19.>
20.-6
21.(1),
(2)点B在双曲线上
(3)或
22.(1)y=,y=x+6;(2);(3)(,2)或(,2).
23.略,(1)R是I的函数;(2)R不是I的反比例函数
24.(1),
(2)20°C
(3)恒温系统最多关闭10小时,蔬菜才能避免受到伤害
25.(1)①1,1,②,
(2)①,②
(3)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
