苏科版数学九上第二章 轴对称图形--圆复习(32张)
文档属性
| 名称 | 苏科版数学九上第二章 轴对称图形--圆复习(32张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 439.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
轴对称图形——圆
制作:没烦恼
2.8圆锥的侧面积
2.1圆
2.2圆的对称性
2.4圆周角
2.5直线和圆的位置关系
2.6正多边形与圆
2.7弧长及扇形的面积
CONTENTS
目录
2.3确定圆的条件
2.1 圆
一、圆的概念
平面内到定点O的距离等于定长r的点的集合.
.p
.o
r
r
.o
.p
r
.o
.p
op<r 点p在⊙o内
op=r 点p在⊙o上
op>r 点p在⊙o外
2.2、圆的对称性
1.定理: 垂直于弦的直径平分弦,并且平分弦所的两条弧.
·o
C
D
A
B
P
若 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
⌒
⌒
③AP=BP,
④AC=BC,
⑤AD=BD.
模型“垂径定理直角三角形”+勾股定理
2.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
二、垂径定理
●O
A
B
C
D
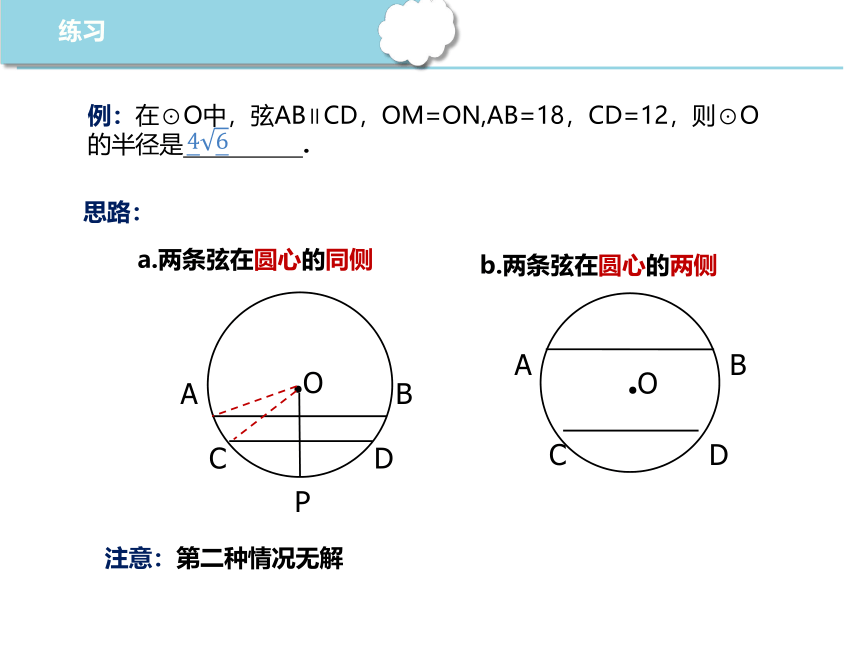
b.两条弦在圆心的两侧
注意:第二种情况无解
●O
A
B
C
D
a.两条弦在圆心的同侧
P
思路:
练习
例:在⊙O中,弦AB∥CD,OM=ON,AB=18,CD=12,则⊙O的半径是 .
【变式】CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,
求CD的长.
A
B
C
D
E
O
.
练习
【答案】26
2.3 确定圆的条件
三角形:圆的内接三角形
圆:三角形的外接圆
圆心:三角形的外心( 三条边垂直平分线的交点)
O
A
B
C
确定圆的条件:不在同一直线上的三个点唯一确定一个圆
2.3 确定圆的条件
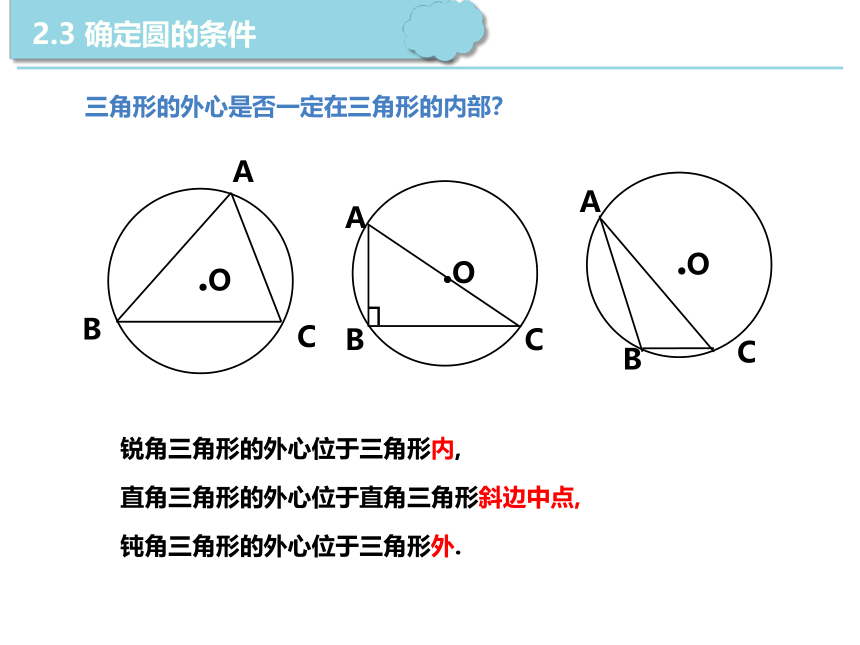
三角形的外心是否一定在三角形的内部?
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
C
A
B
┐
●O
A
B
C
●O
练习
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与⊙O的位置关系是( )
A.点A在⊙O内部 B.点A在⊙O上
C.点A在⊙O外部 D.点A不在⊙O上
【答案】D
2. 在Rt△ ABC中,∠C=90°,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B.
问:(1)A、C、D、E与⊙B的位置关系如何?
(2)AB、AC与⊙B的位置关系如何?
【答案】(1)点A,点E在圆外;点C在圆上;点D在圆内
(2) AB与⊙B相交; AC与⊙B相切,C为切点
练习
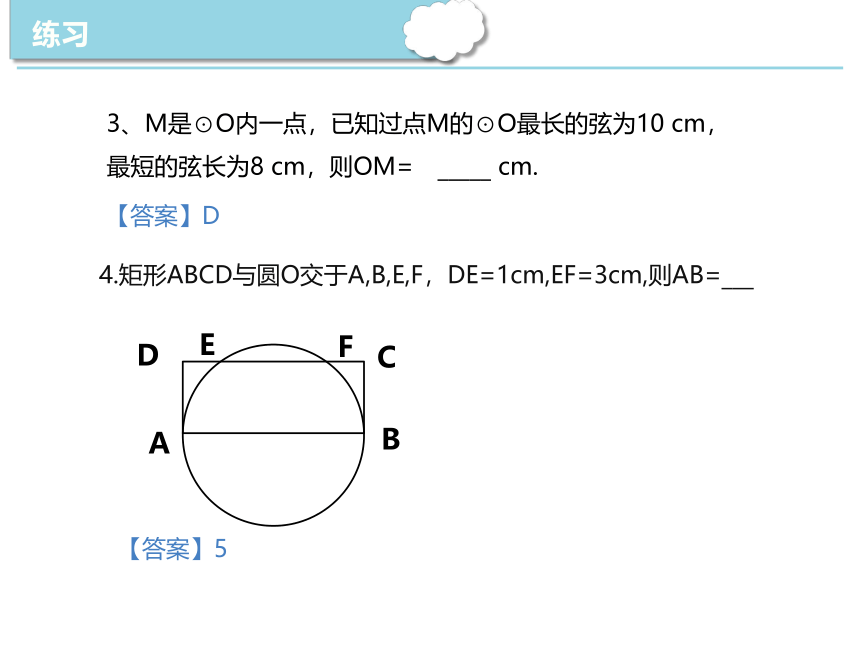
3、M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=?_____ cm.?
4.矩形ABCD与圆O交于A,B,E,F,DE=1cm,EF=3cm,则AB=___
A
B
C
D
E
F
【答案】D
【答案】5
2.4 圆周角
1.内容:在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
A
B
┓
C
A′
B′
C′
┏
·
O
如图:
若AB=A′B′
可推出
AB=A′B′
OD=O′D′
∠AOB=∠A′O′B′
OC=O′C′
⌒
⌒
一、圆心角、弧、弦、弦心距的关系
●O
B
A
C
D
E
●O
A
B
C
●O
A
B
C
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
∠ABC=∠ADC=∠AEC
推论:直径所对的圆周角是 .
90°的圆周角所对的弦是 .
二、圆周角定理及其推论
2.4 圆周角
直角
直径
练习
1、如图1,AB是⊙O的直径,C为圆上一点,弧AC度数为60°,OD⊥BC,D为垂足,且OD=10,则AB=_____,BC=_____;
2、 如图2,⊙O中弧AB的度数为60°,AC是⊙O的直径,那么∠BOC等于 ( );
A.150° B.130° C.120° D.60°
A
B
C
O
图2
A
B
C
O
D
图1
┏
20
20
C
2.5.直线与圆的位置关系
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
1、直线和圆相交
2、直线和圆相切
3、直线和圆相离
d r.
d r.
d r.
<
一、直线与圆的位置关系
=
>
2.5 直线与圆的位置关系
经过半径的外端,并且垂直于这条半径的直线是圆的切线
C
D
●O
A
┐
∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线.
二、切线的判定定理
2.5 直线与圆的位置关系
三、判定切线的方法 :
定义
圆心到直线的距离d=圆的半径r
切线的判定定理
切线的判定定理的两种应用
如果已知直线与圆有交点,往往要作出过这一点的半径,再证明直线垂直于这条半径即可;(连半径,证垂直)
如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.(作垂直,证半径)
2.5 直线与圆的位置关系
四、切线的性质定理
圆的切线垂直于过切点的半径.
∵CD切⊙O于A, OA是⊙O的半径
∴CD⊥OA.
C
D
●O
A
2.5 直线与圆的位置关系
五、切线长定理及其推论
从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.
∵PA,PB切⊙O于A,B
∴PA=PB ∠1=∠2
A
B
P
●O
┗
┏
1
2
练习
2、如图2,PA、PA是圆的切线,A、B为切点,AC为
直径,∠BAC=20°,则∠P= 。
1、已知:如图1,△ABC中,AC=BC,以BC为直径 的⊙O交AB于点D,过点D作DE⊥AC于点E,交 BC的延长线于点F.
求证:(1)AD=BD;(2)DF是⊙O的切线.
图1
A
C
B
P
图2
40°
练习
1.【答案】
证明:(1)连接CD
∵BC为⊙O的直径∴∠BDC=90°
∵AC=BC
∴AD=BD
(2)连接OD
∵ AD=BD,OB=OC
∴OD为的中位线
∴OD∥AC
∵ DE⊥AC
∴ DF⊥OD
∵ OD为半径
∴DF是⊙O的切线
图1
2.5 直线与圆的位置关系
O
A
B
C
A
B
C
I
内心:三角形内切圆的圆心
外心三角形外接圆的圆心
实质 性质
外心 三角形三边垂直平分线的交点 到三角形各顶点的距离相等
内心 三角形三内角角平分线的交点 到三角形各边的距离相等
六、三角形的外接圆和内切圆
直角三角形内切圆半径与三边关系:
三角形的内切圆半径与圆面积:
A
B
C
●
┗
┏
┓
O
D
E
F
┗
┓
┗
┗
●
A
B
C
●
O
●
D
E
F
2.5 直线与圆的位置关系
r(a+b+c)
一、判断。
1、三角形的外心到三角形各边的距离相等; ( )
2、直角三角形的外心是斜边的中点. ( )
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则它的外接圆
半径 ,内切圆半径 ;
2、等边三角形外接圆半径与内切圆半径之比 .
练习
×
√
6.5cm
2cm
2:1
练习
三、选择题:
下列命题正确的是( )
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆
四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三角形的面积为______.
C
30
2.5直线与圆的位置关系
交点个数 名称
0
外离
1
外切
2
相交
1
内切
0
内含
同心圆是内含的特殊情况
d , R , r 的关系
d > R + r
d = R + r
R-r< d < R+ r
d = R - r
d
R
r
d < R - r
七、圆线与圆的位置关系
练习
1.已知⊙O1和⊙O2的半径分别为5和2,O1O2=3,则⊙O1和⊙O2的位置关系是( )
A、外离 B、外切 C、相交 D、内切
2.已知两圆的半径分别是2和3,两圆的圆心距是4,则这两个圆的位置关系是 ( )
A.外离 B.外切 C.相交 D. 内切
3.两圆相切,圆心距为10cm,其中一个圆的半径为6cm,则另一个圆的半径为_____.
4. 已知⊙ O1与⊙ O 2的半径分别为12和2,圆心O1的坐标为(0,8),圆心
O2 的坐标为(-6,0),则两圆的位置关系是______.
B
C
内切
4或16
2.6 正多边形与圆
相关概念
正多边形的中心:外接圆的圆心
中心角:每一边所对圆心角
边心距:中心到正多边形一边的距离
每个内角的度数:
每个中心角的度数:
每个外角的度数:
2.6 正多边形与圆
正多边形的性质:
1.正多边形都只有一个外接圆,圆有无数个内接正多边形.
2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形
3.正多边形都是轴对称图形
4.边数相同的正多边形相似
5.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆
练习
1.若的内接正n边形的边长与的半径相等,则n的值为( )
A.4 B.5 C.6 D.7
2.在圆内接正六边形ABCDEF中,正六边形的边长为2,则这个正六边形的中心角和边心距分别是( )
A.30°,1 B. 45°, C. 60°, D. 120°,2
3.同圆的内接正三角形与内接正方形的边长的比是( )
A. B. C. D.
C
C
A
2.7 弧长及扇形的面积
弧长的计算公式为:
A
B
O
扇形的面积公式为:
·2
S==
2.8 圆锥的侧面积
圆锥侧面积:
圆锥全面积:
母线长:
==n
=S侧+S底
=n+r2
O
P
A
B
r
h
l
练习
例1:小红准备自己动手用纸板制作圆锥形的生日礼帽,如图,圆锥帽底面积半径为9cm,母线长为36cm,请你帮助他们计算制作一个这样的生日礼帽需要纸板的面积为_______.(保留 )
|--36cm---|
9cm
.
324
练习
P
.
A
B
C
例2: 如图,有一圆锥形粮堆,其正视图为边长是6m的正三角形ABC,粮堆的母线AC的中点P处有一老鼠正在偷吃粮食.此时小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是 .
3
轴对称图形——圆
制作:没烦恼
2.8圆锥的侧面积
2.1圆
2.2圆的对称性
2.4圆周角
2.5直线和圆的位置关系
2.6正多边形与圆
2.7弧长及扇形的面积
CONTENTS
目录
2.3确定圆的条件
2.1 圆
一、圆的概念
平面内到定点O的距离等于定长r的点的集合.
.p
.o
r
r
.o
.p
r
.o
.p
op<r 点p在⊙o内
op=r 点p在⊙o上
op>r 点p在⊙o外
2.2、圆的对称性
1.定理: 垂直于弦的直径平分弦,并且平分弦所的两条弧.
·o
C
D
A
B
P
若 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
⌒
⌒
③AP=BP,
④AC=BC,
⑤AD=BD.
模型“垂径定理直角三角形”+勾股定理
2.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
二、垂径定理
●O
A
B
C
D
b.两条弦在圆心的两侧
注意:第二种情况无解
●O
A
B
C
D
a.两条弦在圆心的同侧
P
思路:
练习
例:在⊙O中,弦AB∥CD,OM=ON,AB=18,CD=12,则⊙O的半径是 .
【变式】CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,
求CD的长.
A
B
C
D
E
O
.
练习
【答案】26
2.3 确定圆的条件
三角形:圆的内接三角形
圆:三角形的外接圆
圆心:三角形的外心( 三条边垂直平分线的交点)
O
A
B
C
确定圆的条件:不在同一直线上的三个点唯一确定一个圆
2.3 确定圆的条件
三角形的外心是否一定在三角形的内部?
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
C
A
B
┐
●O
A
B
C
●O
练习
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与⊙O的位置关系是( )
A.点A在⊙O内部 B.点A在⊙O上
C.点A在⊙O外部 D.点A不在⊙O上
【答案】D
2. 在Rt△ ABC中,∠C=90°,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B.
问:(1)A、C、D、E与⊙B的位置关系如何?
(2)AB、AC与⊙B的位置关系如何?
【答案】(1)点A,点E在圆外;点C在圆上;点D在圆内
(2) AB与⊙B相交; AC与⊙B相切,C为切点
练习
3、M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=?_____ cm.?
4.矩形ABCD与圆O交于A,B,E,F,DE=1cm,EF=3cm,则AB=___
A
B
C
D
E
F
【答案】D
【答案】5
2.4 圆周角
1.内容:在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
A
B
┓
C
A′
B′
C′
┏
·
O
如图:
若AB=A′B′
可推出
AB=A′B′
OD=O′D′
∠AOB=∠A′O′B′
OC=O′C′
⌒
⌒
一、圆心角、弧、弦、弦心距的关系
●O
B
A
C
D
E
●O
A
B
C
●O
A
B
C
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
∠ABC=∠ADC=∠AEC
推论:直径所对的圆周角是 .
90°的圆周角所对的弦是 .
二、圆周角定理及其推论
2.4 圆周角
直角
直径
练习
1、如图1,AB是⊙O的直径,C为圆上一点,弧AC度数为60°,OD⊥BC,D为垂足,且OD=10,则AB=_____,BC=_____;
2、 如图2,⊙O中弧AB的度数为60°,AC是⊙O的直径,那么∠BOC等于 ( );
A.150° B.130° C.120° D.60°
A
B
C
O
图2
A
B
C
O
D
图1
┏
20
20
C
2.5.直线与圆的位置关系
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
1、直线和圆相交
2、直线和圆相切
3、直线和圆相离
d r.
d r.
d r.
<
一、直线与圆的位置关系
=
>
2.5 直线与圆的位置关系
经过半径的外端,并且垂直于这条半径的直线是圆的切线
C
D
●O
A
┐
∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线.
二、切线的判定定理
2.5 直线与圆的位置关系
三、判定切线的方法 :
定义
圆心到直线的距离d=圆的半径r
切线的判定定理
切线的判定定理的两种应用
如果已知直线与圆有交点,往往要作出过这一点的半径,再证明直线垂直于这条半径即可;(连半径,证垂直)
如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.(作垂直,证半径)
2.5 直线与圆的位置关系
四、切线的性质定理
圆的切线垂直于过切点的半径.
∵CD切⊙O于A, OA是⊙O的半径
∴CD⊥OA.
C
D
●O
A
2.5 直线与圆的位置关系
五、切线长定理及其推论
从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.
∵PA,PB切⊙O于A,B
∴PA=PB ∠1=∠2
A
B
P
●O
┗
┏
1
2
练习
2、如图2,PA、PA是圆的切线,A、B为切点,AC为
直径,∠BAC=20°,则∠P= 。
1、已知:如图1,△ABC中,AC=BC,以BC为直径 的⊙O交AB于点D,过点D作DE⊥AC于点E,交 BC的延长线于点F.
求证:(1)AD=BD;(2)DF是⊙O的切线.
图1
A
C
B
P
图2
40°
练习
1.【答案】
证明:(1)连接CD
∵BC为⊙O的直径∴∠BDC=90°
∵AC=BC
∴AD=BD
(2)连接OD
∵ AD=BD,OB=OC
∴OD为的中位线
∴OD∥AC
∵ DE⊥AC
∴ DF⊥OD
∵ OD为半径
∴DF是⊙O的切线
图1
2.5 直线与圆的位置关系
O
A
B
C
A
B
C
I
内心:三角形内切圆的圆心
外心三角形外接圆的圆心
实质 性质
外心 三角形三边垂直平分线的交点 到三角形各顶点的距离相等
内心 三角形三内角角平分线的交点 到三角形各边的距离相等
六、三角形的外接圆和内切圆
直角三角形内切圆半径与三边关系:
三角形的内切圆半径与圆面积:
A
B
C
●
┗
┏
┓
O
D
E
F
┗
┓
┗
┗
●
A
B
C
●
O
●
D
E
F
2.5 直线与圆的位置关系
r(a+b+c)
一、判断。
1、三角形的外心到三角形各边的距离相等; ( )
2、直角三角形的外心是斜边的中点. ( )
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则它的外接圆
半径 ,内切圆半径 ;
2、等边三角形外接圆半径与内切圆半径之比 .
练习
×
√
6.5cm
2cm
2:1
练习
三、选择题:
下列命题正确的是( )
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆
四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三角形的面积为______.
C
30
2.5直线与圆的位置关系
交点个数 名称
0
外离
1
外切
2
相交
1
内切
0
内含
同心圆是内含的特殊情况
d , R , r 的关系
d > R + r
d = R + r
R-r< d < R+ r
d = R - r
d
R
r
d < R - r
七、圆线与圆的位置关系
练习
1.已知⊙O1和⊙O2的半径分别为5和2,O1O2=3,则⊙O1和⊙O2的位置关系是( )
A、外离 B、外切 C、相交 D、内切
2.已知两圆的半径分别是2和3,两圆的圆心距是4,则这两个圆的位置关系是 ( )
A.外离 B.外切 C.相交 D. 内切
3.两圆相切,圆心距为10cm,其中一个圆的半径为6cm,则另一个圆的半径为_____.
4. 已知⊙ O1与⊙ O 2的半径分别为12和2,圆心O1的坐标为(0,8),圆心
O2 的坐标为(-6,0),则两圆的位置关系是______.
B
C
内切
4或16
2.6 正多边形与圆
相关概念
正多边形的中心:外接圆的圆心
中心角:每一边所对圆心角
边心距:中心到正多边形一边的距离
每个内角的度数:
每个中心角的度数:
每个外角的度数:
2.6 正多边形与圆
正多边形的性质:
1.正多边形都只有一个外接圆,圆有无数个内接正多边形.
2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形
3.正多边形都是轴对称图形
4.边数相同的正多边形相似
5.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆
练习
1.若的内接正n边形的边长与的半径相等,则n的值为( )
A.4 B.5 C.6 D.7
2.在圆内接正六边形ABCDEF中,正六边形的边长为2,则这个正六边形的中心角和边心距分别是( )
A.30°,1 B. 45°, C. 60°, D. 120°,2
3.同圆的内接正三角形与内接正方形的边长的比是( )
A. B. C. D.
C
C
A
2.7 弧长及扇形的面积
弧长的计算公式为:
A
B
O
扇形的面积公式为:
·2
S==
2.8 圆锥的侧面积
圆锥侧面积:
圆锥全面积:
母线长:
==n
=S侧+S底
=n+r2
O
P
A
B
r
h
l
练习
例1:小红准备自己动手用纸板制作圆锥形的生日礼帽,如图,圆锥帽底面积半径为9cm,母线长为36cm,请你帮助他们计算制作一个这样的生日礼帽需要纸板的面积为_______.(保留 )
|--36cm---|
9cm
.
324
练习
P
.
A
B
C
例2: 如图,有一圆锥形粮堆,其正视图为边长是6m的正三角形ABC,粮堆的母线AC的中点P处有一老鼠正在偷吃粮食.此时小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是 .
3
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
