5.4-1 多边形的内角和 课件(共18张PPT) 鲁教版(五四制)数学八年级上册
文档属性
| 名称 | 5.4-1 多边形的内角和 课件(共18张PPT) 鲁教版(五四制)数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 514.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 15:18:03 | ||
图片预览






文档简介
(共18张PPT)
5.4-1 多边形的内角和
学习目标
1.经历探索多边形内角和公式的过程,体会“转化”、“分类讨论”的数学思想.
2.熟练掌握多边形内角和与外角和公式,并会运用公式解决问题.
温顾
1.定义:多边形是由一些 上的 首尾 相连组成的 平面图形。
不在同一条直线
线段
顺次
封闭
多边形的相关概念
边
内角
顶点
对角线
外角
2.各部分名称:如图
顶点、边、内角、外角、对角线
问题:n边形有多少条对角线?
能将多边形分成几个三角形?
温顾
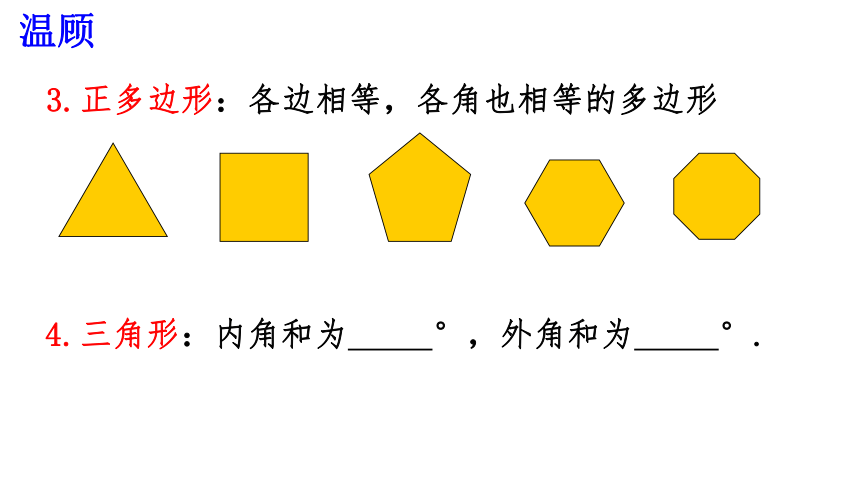
3.正多边形:各边相等,各角也相等的多边形
4.三角形:内角和为 °,外角和为 °.
问题导入
上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗 与同伴交流.
小明利用如图的方法求出了该五边形的五个内角的和,你知道他是怎样做的吗
问题探究
B
A
C
D
E
五边形内角和=3×180°=540°
按照同样的方法:
六边形能分成多少个三角形
七边形能分成多少个三角形
八边形能分成多少个三角形
……
想一想
n边形呢 (n是大于或等于3的自然数)
你能确定n边形的内角和吗
多边形 边数 分成三角形的个数 图形 内角和 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2) ·180°
(n-2)·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
…
…
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
知新
还有其他的方法求出五边形的内角和吗
180°× 4–180°= 540°
议一议
B
A
E
C
D
F
还有其他的方法求出五边形的内角和吗
180°× 5–360°= 540°
议一议
B
A
E
C
F
D
还有其他的方法求出五边形的内角和吗
180°× 4–180°= 540°
议一议
B
A
E
C
F
D
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
知新
1.九边形的内角和等于___________.
2.如果一个多边形的内角和是1440度,那么这是____边形。
3.已知多边形的每个内角都等于150°,求这个多边形的边数?
4.一个多边形当边数增加1时,它的内角和增加 .
5.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540° C.720° D.900°
新知应用
正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度 正n边形的内角是多少度
想一想
正n边形的内角=
剪掉一张长方形的纸片的一个角后,纸片还剩几个角 剪下角后得到的多边形的内角和是多少度 与同伴交流.
新知拓展
巩固练习
1.一个多边形的内角和等于 1260°,从它的一个顶点出发,可以作对角线的条数是( )
A.4 B.6 C.7 D.9
2.小东在计算多边形的内角和时不小心多加了一个内角,得到的和为 1350°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
3.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
巩固练习
4.一个多边形的各边都相等,周长是84,且它的内角和为900°,则它的边长是 .
5.如图,求∠A+∠B+∠C+∠D+∠E+∠F= ( )
A、720°B、540°C、180°D、360°
5.4-1 多边形的内角和
学习目标
1.经历探索多边形内角和公式的过程,体会“转化”、“分类讨论”的数学思想.
2.熟练掌握多边形内角和与外角和公式,并会运用公式解决问题.
温顾
1.定义:多边形是由一些 上的 首尾 相连组成的 平面图形。
不在同一条直线
线段
顺次
封闭
多边形的相关概念
边
内角
顶点
对角线
外角
2.各部分名称:如图
顶点、边、内角、外角、对角线
问题:n边形有多少条对角线?
能将多边形分成几个三角形?
温顾
3.正多边形:各边相等,各角也相等的多边形
4.三角形:内角和为 °,外角和为 °.
问题导入
上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗 与同伴交流.
小明利用如图的方法求出了该五边形的五个内角的和,你知道他是怎样做的吗
问题探究
B
A
C
D
E
五边形内角和=3×180°=540°
按照同样的方法:
六边形能分成多少个三角形
七边形能分成多少个三角形
八边形能分成多少个三角形
……
想一想
n边形呢 (n是大于或等于3的自然数)
你能确定n边形的内角和吗
多边形 边数 分成三角形的个数 图形 内角和 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2) ·180°
(n-2)·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
…
…
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
知新
还有其他的方法求出五边形的内角和吗
180°× 4–180°= 540°
议一议
B
A
E
C
D
F
还有其他的方法求出五边形的内角和吗
180°× 5–360°= 540°
议一议
B
A
E
C
F
D
还有其他的方法求出五边形的内角和吗
180°× 4–180°= 540°
议一议
B
A
E
C
F
D
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
知新
1.九边形的内角和等于___________.
2.如果一个多边形的内角和是1440度,那么这是____边形。
3.已知多边形的每个内角都等于150°,求这个多边形的边数?
4.一个多边形当边数增加1时,它的内角和增加 .
5.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540° C.720° D.900°
新知应用
正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度 正n边形的内角是多少度
想一想
正n边形的内角=
剪掉一张长方形的纸片的一个角后,纸片还剩几个角 剪下角后得到的多边形的内角和是多少度 与同伴交流.
新知拓展
巩固练习
1.一个多边形的内角和等于 1260°,从它的一个顶点出发,可以作对角线的条数是( )
A.4 B.6 C.7 D.9
2.小东在计算多边形的内角和时不小心多加了一个内角,得到的和为 1350°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
3.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
巩固练习
4.一个多边形的各边都相等,周长是84,且它的内角和为900°,则它的边长是 .
5.如图,求∠A+∠B+∠C+∠D+∠E+∠F= ( )
A、720°B、540°C、180°D、360°
