人教版8年级下册 数学第十九章 一次函数 学案
文档属性
| 名称 | 人教版8年级下册 数学第十九章 一次函数 学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 187.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 17:48:20 | ||
图片预览


文档简介
执教内容 一次函数的专题复习(1)
教学目标 1知识与技能目标 掌握根据已知条件确定一次函数的表达式; 会用待定系数法确定一次函数的表达式; 理解当k和b的不同取值范围时,一次函数图象的变化情况; 掌握一次函数与二元一次方程以及一元一次不等式的关系。
2:过程与方法目标 通过将作业前置将一次函数的相关基本知识点进行一个简单的复习,并使学生掌握基本的求解一次函数解析式的方法; 在课堂练习中,通过题组的练习将知识点再一次提升,使每个层次的学生都能达到所要求的目标; 通过能力的提升达到学生思维的发散,将不用的知识点作一个技能的叠加。
3:情感态度与价值观目标 通过将题目进行分层,使得班级的每个学生都能明确自身需要的到达的层次,每个学生在课堂上都能有所收获,增加其在数学总复习中的信心,再次建立学习和巩固数学的信心;对于优生而言,技能的叠加从而达到能力上的提升,是学生在未来的学习中能够学有所想,懂得将所学的知识进行整合,形成一个较完整的知识网络。
教学重点与难点 教学重点 1:根据所给条件求一次函数的解析式; 2:通过图象分析,理解一次函数与二元一次方程,一元一次不等式的关系,从而运用图象解决相应的问题; 3:通过对k,b正负性的判断,正确判断一次函数图象的变化情况。
教学难点 会正确利用图象解决相应的一次函数与其他知识的叠加问题。
教学手段 运用多媒体课件和教具
教学过程 教学过程 环节 教师活动 学生活动 设计意图
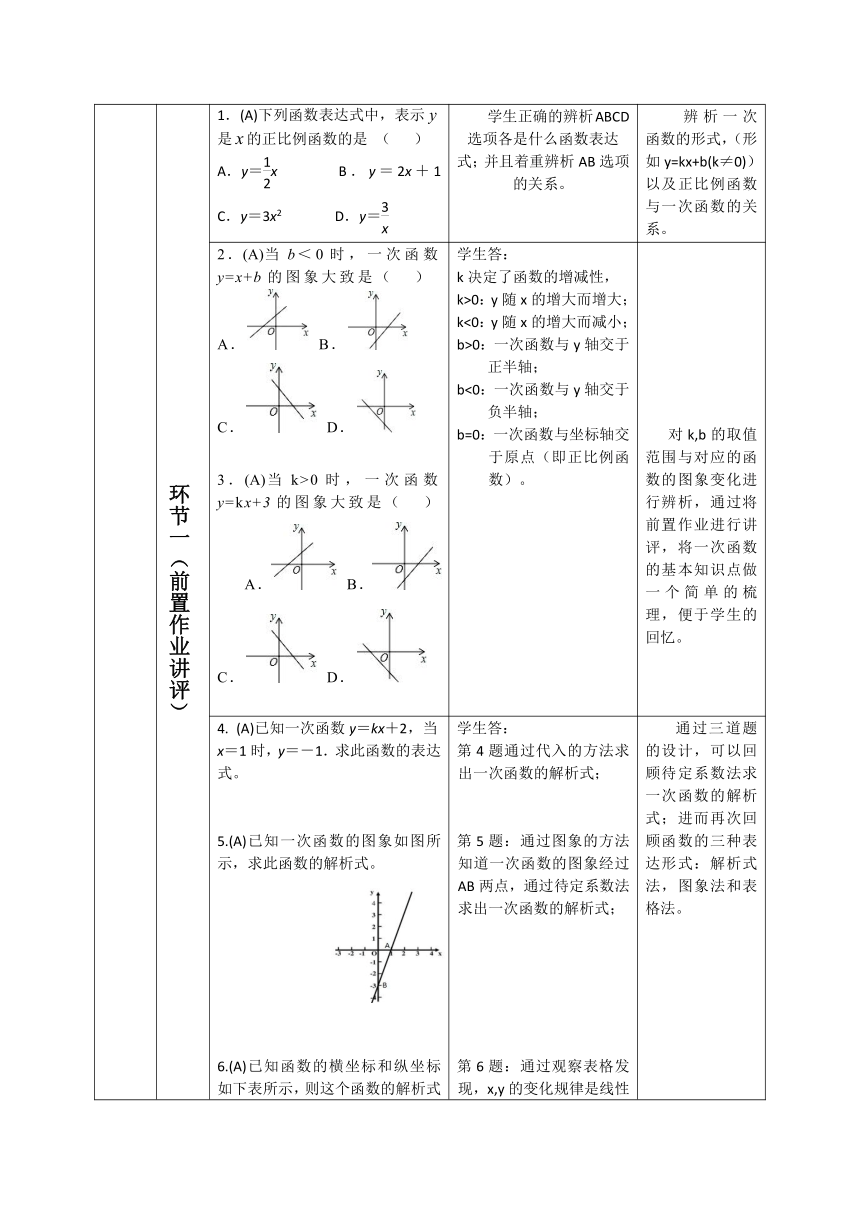
环节一(前置作业讲评) 1.(A)下列函数表达式中,表示是的正比例函数的是 ( ) A.y=x B.y=2x+1 C.y=3x2 D.y= 学生正确的辨析ABCD选项各是什么函数表达式;并且着重辨析AB选项的关系。 辨析一次函数的形式,(形如y=kx+b(k≠0))以及正比例函数与一次函数的关系。
2.(A)当b<0时,一次函数y=x+b的图象大致是( ) A. B. C. D. 3.(A)当k>0时,一次函数y=kx+3的图象大致是( ) A. B. C. D. 学生答: k决定了函数的增减性, k>0:y随x的增大而增大; k<0:y随x的增大而减小; b>0:一次函数与y轴交于正半轴; b<0:一次函数与y轴交于负半轴; b=0:一次函数与坐标轴交于原点(即正比例函数)。 对k,b的取值范围与对应的函数的图象变化进行辨析,通过将前置作业进行讲评,将一次函数的基本知识点做一个简单的梳理,便于学生的回忆。
(A)已知一次函数y=kx+2,当x=1时,y=-1.求此函数的表达式。 5.(A)已知一次函数的图象如图所示,求此函数的解析式。 6.(A)已知函数的横坐标和纵坐标如下表所示,则这个函数的解析式是多少? x-1012y630-3
学生答: 第4题通过代入的方法求出一次函数的解析式; 第5题:通过图象的方法知道一次函数的图象经过AB两点,通过待定系数法求出一次函数的解析式; 第6题:通过观察表格发现,x,y的变化规律是线性的,故而满足一次函数的形式,进而可以写出一次函数的解析式; 通过三道题的设计,可以回顾待定系数法求一次函数的解析式;进而再次回顾函数的三种表达形式:解析式法,图象法和表格法。
环节二(例题解析) 例题1、一次函数的图象如图1所示.函数与x轴交于点A(4,0),与y轴交于点B; (1)(A)函数值随增大而___; (2)(A)求函数的解析式_______; (3)(A)当= ,; (4)(B)当时,自变量的取值范围是 ; (5)(B)不等式的解集为 ; (6)(B)函数与坐标系所构成的△ABO的面积是____; (
图1
4
)(7)(C)不等式的解集为_____. 学生答: 第一问:通过图象可以知道y随x的增大而减小 第二问:可以通过点A的代入求出一次函数的解析式; 第三问:一种是纯代数方程思想;一种是图象法,看成是一次函数与X轴交点的横坐标。 第四、五问:一种是纯代数,看成是一元一次不等式求解;一种是图象法,看成是一次函数当y<0的时候的解集。 第六问:找出函数与坐标轴的两个交点,但是三角形的面积计算公式。 第七问:通过将一次函数向右平移3个单位得到。 此题组在层次的设计上进行了分成,适合各个层次的学生,使学生不至于无事可做,学生可以算自己会算的题目,特别是后面的题组可以发现,通过图象法可以让学生很轻易地得出答案,体会到数形结合的好处和优势。最后一问则是考虑到函数的左右平移变换,不用求解,直接通过图象的平移即可得到答案,体现了图象法在解决题目的好用之处。
环节三(练习巩固) 环节三(练习巩固) 在图2的坐标系中,画出直线:和直线:;若直线和直线相交于C点,且直线、分别与轴交于A,D两点 (1)(A)方程的解是 ; (2)(A)不等式的解集是 ; (3)(B)不等式的解集为_______. (4)(B)利用图象求出不等式的解集为: ; (5)(B)利用图象解方程组得 . (6)(B)△ABD的面积是 ; (
图
2
) 学生答: 利用图象可以很快的回答出第一问即是与x轴的交点的横坐标, 第二问:通过代数解决可以,也可以看成是在x轴上方对应的图象在x轴的投影的解集。 第三问:和上面例题的第七问是一样的方法,通过左右平移可以得到;第四问:通过观察两个图象的交点,我们发现,不等式即是≥进而找到交点,分区域,比大小的方法解决。 此题组旨在让学生再一次巩固图象法解决问题的方法,具体需要找什么条件,关键的交点在哪?
2.(A)已知甲、乙两个函数图象上部分点的横坐标x与对应的纵坐标y分别如下表所示.若这两个函数图象仅有一个交点,则交点的纵坐标y是 ( ) A.0 B.3 (
甲
乙
)C.4 D.6 学生答:两个表格中,相同的横纵坐标即是交点,取纵坐标y=3 识表格得出表格所显示的函数的两个特征。
3. (B)若函数的图象如图3所示,则关于的不等式 的解集为( ) B. (
图3
)C. D. 4. (C)若函数的图象如图4所示,则关于的不等式 的解集为( ) B. (
图4
)C. D. 学生答:通过平移,将函数向右平移3个单位,与x轴的交点也向右平移3个单位,得到x<5 学生答:不知道。误以为和第3题是一样,简单的左右平移。 再次巩固图象的左右平移对于解决相应的不等式的解集的好处。第4题的设置,告诉学生知识不是生搬硬套的,一直都是简单的左右平移,而应该注意关注式子的结构特征,加以转换成我们需要的式子结构。
5.如图,直线y=-x+2分别与x,y轴交于点B,C,点A(-2,0),P是直线BC上的动点。 (1)(A)求∠ABC的大小; (2)(B)求点P的坐标, 使∠APO=30°; (3)(C)在平面直角坐标系中,平移直线BC,试探索:当BC在不同位置时,∠APO=30°的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由。 作为本节课的能力提高题,对于少部分学生而言还是很有必要的,对于学生在思维的拓展方面,以及技能的叠加方面,有个横向和纵向的提升。
板书设计 (
图
2
) (
图1
4
) 一次函数专题复习(1) 概念:一次函数 正比例函数 K决定 b决定 三种表示法: 草稿版面
教学反思
教学目标 1知识与技能目标 掌握根据已知条件确定一次函数的表达式; 会用待定系数法确定一次函数的表达式; 理解当k和b的不同取值范围时,一次函数图象的变化情况; 掌握一次函数与二元一次方程以及一元一次不等式的关系。
2:过程与方法目标 通过将作业前置将一次函数的相关基本知识点进行一个简单的复习,并使学生掌握基本的求解一次函数解析式的方法; 在课堂练习中,通过题组的练习将知识点再一次提升,使每个层次的学生都能达到所要求的目标; 通过能力的提升达到学生思维的发散,将不用的知识点作一个技能的叠加。
3:情感态度与价值观目标 通过将题目进行分层,使得班级的每个学生都能明确自身需要的到达的层次,每个学生在课堂上都能有所收获,增加其在数学总复习中的信心,再次建立学习和巩固数学的信心;对于优生而言,技能的叠加从而达到能力上的提升,是学生在未来的学习中能够学有所想,懂得将所学的知识进行整合,形成一个较完整的知识网络。
教学重点与难点 教学重点 1:根据所给条件求一次函数的解析式; 2:通过图象分析,理解一次函数与二元一次方程,一元一次不等式的关系,从而运用图象解决相应的问题; 3:通过对k,b正负性的判断,正确判断一次函数图象的变化情况。
教学难点 会正确利用图象解决相应的一次函数与其他知识的叠加问题。
教学手段 运用多媒体课件和教具
教学过程 教学过程 环节 教师活动 学生活动 设计意图
环节一(前置作业讲评) 1.(A)下列函数表达式中,表示是的正比例函数的是 ( ) A.y=x B.y=2x+1 C.y=3x2 D.y= 学生正确的辨析ABCD选项各是什么函数表达式;并且着重辨析AB选项的关系。 辨析一次函数的形式,(形如y=kx+b(k≠0))以及正比例函数与一次函数的关系。
2.(A)当b<0时,一次函数y=x+b的图象大致是( ) A. B. C. D. 3.(A)当k>0时,一次函数y=kx+3的图象大致是( ) A. B. C. D. 学生答: k决定了函数的增减性, k>0:y随x的增大而增大; k<0:y随x的增大而减小; b>0:一次函数与y轴交于正半轴; b<0:一次函数与y轴交于负半轴; b=0:一次函数与坐标轴交于原点(即正比例函数)。 对k,b的取值范围与对应的函数的图象变化进行辨析,通过将前置作业进行讲评,将一次函数的基本知识点做一个简单的梳理,便于学生的回忆。
(A)已知一次函数y=kx+2,当x=1时,y=-1.求此函数的表达式。 5.(A)已知一次函数的图象如图所示,求此函数的解析式。 6.(A)已知函数的横坐标和纵坐标如下表所示,则这个函数的解析式是多少? x-1012y630-3
学生答: 第4题通过代入的方法求出一次函数的解析式; 第5题:通过图象的方法知道一次函数的图象经过AB两点,通过待定系数法求出一次函数的解析式; 第6题:通过观察表格发现,x,y的变化规律是线性的,故而满足一次函数的形式,进而可以写出一次函数的解析式; 通过三道题的设计,可以回顾待定系数法求一次函数的解析式;进而再次回顾函数的三种表达形式:解析式法,图象法和表格法。
环节二(例题解析) 例题1、一次函数的图象如图1所示.函数与x轴交于点A(4,0),与y轴交于点B; (1)(A)函数值随增大而___; (2)(A)求函数的解析式_______; (3)(A)当= ,; (4)(B)当时,自变量的取值范围是 ; (5)(B)不等式的解集为 ; (6)(B)函数与坐标系所构成的△ABO的面积是____; (
图1
4
)(7)(C)不等式的解集为_____. 学生答: 第一问:通过图象可以知道y随x的增大而减小 第二问:可以通过点A的代入求出一次函数的解析式; 第三问:一种是纯代数方程思想;一种是图象法,看成是一次函数与X轴交点的横坐标。 第四、五问:一种是纯代数,看成是一元一次不等式求解;一种是图象法,看成是一次函数当y<0的时候的解集。 第六问:找出函数与坐标轴的两个交点,但是三角形的面积计算公式。 第七问:通过将一次函数向右平移3个单位得到。 此题组在层次的设计上进行了分成,适合各个层次的学生,使学生不至于无事可做,学生可以算自己会算的题目,特别是后面的题组可以发现,通过图象法可以让学生很轻易地得出答案,体会到数形结合的好处和优势。最后一问则是考虑到函数的左右平移变换,不用求解,直接通过图象的平移即可得到答案,体现了图象法在解决题目的好用之处。
环节三(练习巩固) 环节三(练习巩固) 在图2的坐标系中,画出直线:和直线:;若直线和直线相交于C点,且直线、分别与轴交于A,D两点 (1)(A)方程的解是 ; (2)(A)不等式的解集是 ; (3)(B)不等式的解集为_______. (4)(B)利用图象求出不等式的解集为: ; (5)(B)利用图象解方程组得 . (6)(B)△ABD的面积是 ; (
图
2
) 学生答: 利用图象可以很快的回答出第一问即是与x轴的交点的横坐标, 第二问:通过代数解决可以,也可以看成是在x轴上方对应的图象在x轴的投影的解集。 第三问:和上面例题的第七问是一样的方法,通过左右平移可以得到;第四问:通过观察两个图象的交点,我们发现,不等式即是≥进而找到交点,分区域,比大小的方法解决。 此题组旨在让学生再一次巩固图象法解决问题的方法,具体需要找什么条件,关键的交点在哪?
2.(A)已知甲、乙两个函数图象上部分点的横坐标x与对应的纵坐标y分别如下表所示.若这两个函数图象仅有一个交点,则交点的纵坐标y是 ( ) A.0 B.3 (
甲
乙
)C.4 D.6 学生答:两个表格中,相同的横纵坐标即是交点,取纵坐标y=3 识表格得出表格所显示的函数的两个特征。
3. (B)若函数的图象如图3所示,则关于的不等式 的解集为( ) B. (
图3
)C. D. 4. (C)若函数的图象如图4所示,则关于的不等式 的解集为( ) B. (
图4
)C. D. 学生答:通过平移,将函数向右平移3个单位,与x轴的交点也向右平移3个单位,得到x<5 学生答:不知道。误以为和第3题是一样,简单的左右平移。 再次巩固图象的左右平移对于解决相应的不等式的解集的好处。第4题的设置,告诉学生知识不是生搬硬套的,一直都是简单的左右平移,而应该注意关注式子的结构特征,加以转换成我们需要的式子结构。
5.如图,直线y=-x+2分别与x,y轴交于点B,C,点A(-2,0),P是直线BC上的动点。 (1)(A)求∠ABC的大小; (2)(B)求点P的坐标, 使∠APO=30°; (3)(C)在平面直角坐标系中,平移直线BC,试探索:当BC在不同位置时,∠APO=30°的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由。 作为本节课的能力提高题,对于少部分学生而言还是很有必要的,对于学生在思维的拓展方面,以及技能的叠加方面,有个横向和纵向的提升。
板书设计 (
图
2
) (
图1
4
) 一次函数专题复习(1) 概念:一次函数 正比例函数 K决定 b决定 三种表示法: 草稿版面
教学反思
