27.3 第1课时 弧长、扇形面积公式 课件 华东师大版数学九年级下册(20张PPT)
文档属性
| 名称 | 27.3 第1课时 弧长、扇形面积公式 课件 华东师大版数学九年级下册(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 943.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 17:54:47 | ||
图片预览








文档简介
(共20张PPT)
第27章 圆
27.3 圆中的计算问题
第1课时 弧长、扇形面积公式
1.知道弧长、扇形面积的公式,会推导两者之间的关系.
2.会恰当熟练地运用公式计算弧长及扇形面积,增强数学应用能力.
◎重点:弧长及扇形面积公式的推导及应用.
◎难点:弧长及扇形面积公式的应用.
一块空旷的草地上有一根柱子,柱子上拴着一条长3米的绳子,绳子的另一端拴着一条狗.(1)这条狗的最大活动区域有多大?(2)如果这条狗只能绕柱子转过n°,那么它的最大活动区域有多大?
弧长公式
阅读课本本课时开始至第一个“探索”部分的内容,完成下面问题.
1.半径为r的圆的周长为 2πr ,圆的周长可以看作是 360° 的圆心角所对的弧长.
2πr
360°
2.填表.
圆心角的度数 1° 90° 180° n°
占周角的比例
所对弧占圆周长的比例
弧长
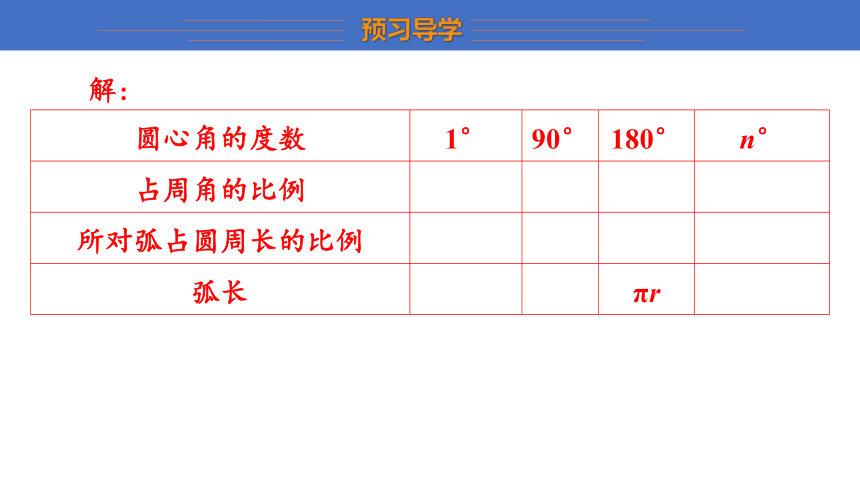
解:
圆心角的度数 1° 90° 180° n°
占周角的比例
所对弧占圆周长的比例
弧长 πr
解:
归纳总结 如果弧长为l,圆心角的度数为n,圆的半径为r,那么弧长公式为l= .
·导学建议·
通过回顾圆周长公式,加强新旧知识的联系,类比旧知识,学习新知识.
扇形的面积
阅读课本本课时第二个“思考”至“例1”的内容,完成下面问题.
1.扇形是由组成圆心角的两条 半径 和圆心角所对的 弧 围成的图形.
半径
弧
2.半径为r的圆的面积为 πr2 ,圆心角是1°时,占整个周角的 ,因此圆心角是1°的扇形面积占圆的面积的 ,由此可得,圆心角是1°,半径为r的扇形的面积是 .
归纳总结 半径为r,圆心角为n°的扇形面积S= .
πr2
【讨论】已知扇形的半径是r,弧长为l,请你根据弧长公式和面积公式,用l,r表示扇形的面积.
答:S==r×=lr.
·导学建议·
扇形公式S=lr与三角形面积公式类似,指导学生记忆时可把弧长看作底,半径看成高.
1.圆心角为120°,半径为6 cm的扇形的弧长是 4π cm.
2.圆心角是60°且半径为2的扇形面积为 π (结果保留π).
4π
π
利用弧长公式进行计算
1.(1)已知圆弧的半径为3 cm,圆心角为120°,则此圆弧的长度为 2π cm .
(2)有一条弧的长为2π cm,半径为2 cm,则这条弧所对的圆心角的度数是 180° .
(3)一条长度为10π cm的弧所对的圆心角为60°,则这条弧所在的圆的半径是 30 cm .
2π cm
180°
30 cm
利用扇形面积公式进行计算
2.(1)在半径为6的☉O中,30°圆心角所对的扇形的面积为 3π .
(2)若扇形的面积为3π,圆心角为60°,则该扇形的半径为 3 .
(3)若扇形的面积为3π,半径是3,则该扇形的圆心角为 120° .
3π
3
120°
3.(1)已知一个扇形的半径为3,弧长为3,则这个扇形的面积为 .
(2)如图,将长为8 cm的铁丝AB首尾相接围成半径为2 cm的扇形,则S扇形= 4 cm2.
4
变式演练 如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( D )
D
A.6 B.7 C.8 D.9
求不规则图形的面积
4.如图,AB是☉O的直径,弦CD⊥AB,∠C=30°,CD=2,则S阴影=( D )
A.π B.2π
C. D.π
D
方法归纳交流 求图形面积的方法一般有两种:规则图形直接使用面积公式计算;不规则图形则进行割补,拼成 规则图形 再进行计算.
规则图
形
(1)已知扇形的面积为12π cm2,圆心角为120°,则扇形的弧长为 4π cm.
(2)圆心角为120°的扇形的弧长是6π,则此扇形的面积是 27π .
4π
27π
第27章 圆
27.3 圆中的计算问题
第1课时 弧长、扇形面积公式
1.知道弧长、扇形面积的公式,会推导两者之间的关系.
2.会恰当熟练地运用公式计算弧长及扇形面积,增强数学应用能力.
◎重点:弧长及扇形面积公式的推导及应用.
◎难点:弧长及扇形面积公式的应用.
一块空旷的草地上有一根柱子,柱子上拴着一条长3米的绳子,绳子的另一端拴着一条狗.(1)这条狗的最大活动区域有多大?(2)如果这条狗只能绕柱子转过n°,那么它的最大活动区域有多大?
弧长公式
阅读课本本课时开始至第一个“探索”部分的内容,完成下面问题.
1.半径为r的圆的周长为 2πr ,圆的周长可以看作是 360° 的圆心角所对的弧长.
2πr
360°
2.填表.
圆心角的度数 1° 90° 180° n°
占周角的比例
所对弧占圆周长的比例
弧长
解:
圆心角的度数 1° 90° 180° n°
占周角的比例
所对弧占圆周长的比例
弧长 πr
解:
归纳总结 如果弧长为l,圆心角的度数为n,圆的半径为r,那么弧长公式为l= .
·导学建议·
通过回顾圆周长公式,加强新旧知识的联系,类比旧知识,学习新知识.
扇形的面积
阅读课本本课时第二个“思考”至“例1”的内容,完成下面问题.
1.扇形是由组成圆心角的两条 半径 和圆心角所对的 弧 围成的图形.
半径
弧
2.半径为r的圆的面积为 πr2 ,圆心角是1°时,占整个周角的 ,因此圆心角是1°的扇形面积占圆的面积的 ,由此可得,圆心角是1°,半径为r的扇形的面积是 .
归纳总结 半径为r,圆心角为n°的扇形面积S= .
πr2
【讨论】已知扇形的半径是r,弧长为l,请你根据弧长公式和面积公式,用l,r表示扇形的面积.
答:S==r×=lr.
·导学建议·
扇形公式S=lr与三角形面积公式类似,指导学生记忆时可把弧长看作底,半径看成高.
1.圆心角为120°,半径为6 cm的扇形的弧长是 4π cm.
2.圆心角是60°且半径为2的扇形面积为 π (结果保留π).
4π
π
利用弧长公式进行计算
1.(1)已知圆弧的半径为3 cm,圆心角为120°,则此圆弧的长度为 2π cm .
(2)有一条弧的长为2π cm,半径为2 cm,则这条弧所对的圆心角的度数是 180° .
(3)一条长度为10π cm的弧所对的圆心角为60°,则这条弧所在的圆的半径是 30 cm .
2π cm
180°
30 cm
利用扇形面积公式进行计算
2.(1)在半径为6的☉O中,30°圆心角所对的扇形的面积为 3π .
(2)若扇形的面积为3π,圆心角为60°,则该扇形的半径为 3 .
(3)若扇形的面积为3π,半径是3,则该扇形的圆心角为 120° .
3π
3
120°
3.(1)已知一个扇形的半径为3,弧长为3,则这个扇形的面积为 .
(2)如图,将长为8 cm的铁丝AB首尾相接围成半径为2 cm的扇形,则S扇形= 4 cm2.
4
变式演练 如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( D )
D
A.6 B.7 C.8 D.9
求不规则图形的面积
4.如图,AB是☉O的直径,弦CD⊥AB,∠C=30°,CD=2,则S阴影=( D )
A.π B.2π
C. D.π
D
方法归纳交流 求图形面积的方法一般有两种:规则图形直接使用面积公式计算;不规则图形则进行割补,拼成 规则图形 再进行计算.
规则图
形
(1)已知扇形的面积为12π cm2,圆心角为120°,则扇形的弧长为 4π cm.
(2)圆心角为120°的扇形的弧长是6π,则此扇形的面积是 27π .
4π
27π
