1.3 不共线三点确定二次函数的表达式 课件 湘教版数学九年级下册(18张PPT)
文档属性
| 名称 | 1.3 不共线三点确定二次函数的表达式 课件 湘教版数学九年级下册(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 315.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 17:55:43 | ||
图片预览





文档简介
(共18张PPT)
第一章 二次函数
1.3 不共线三点确定二次函数的表达式
复习导入
y=ax2+bx+c
对称轴是:
顶点坐标是:
当 时,函数达到最大值(当a<0)或最小值(当a>0): .
复习导入
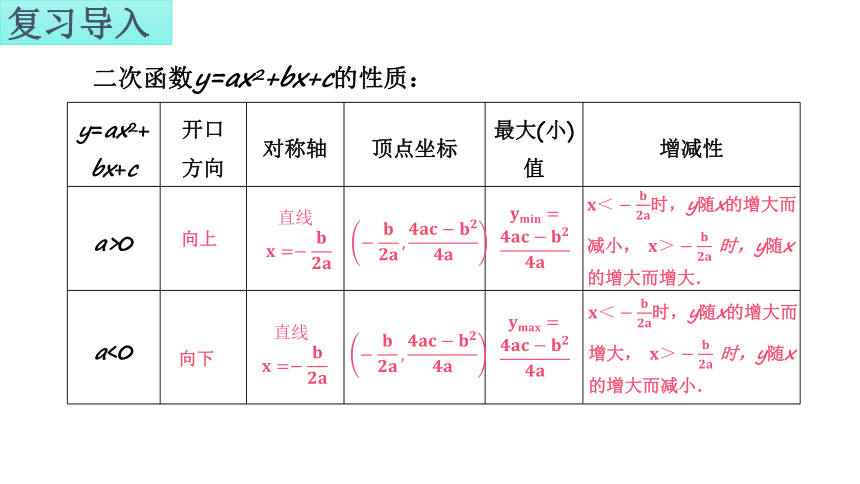
二次函数y=ax2+bx+c的性质:
y=ax2+bx+c 开口 方向 对称轴 顶点坐标 最大(小)值 增减性
a>0
a<0
向上
向下
时,y随x的增大而减小, 时,y随x的增大而增大.
时,y随x的增大而增大, 时,y随x的增大而减小.
1、怎样用待定系数法确定一次函数的解析式?
y=kx+b (k≠0)
系数k,
b待定
找两个点
确定两个方程
解二元一次方程组
2、二次函数的表达式有哪些?
一般式: y=ax2+bx+c
顶点式: y=a(x-h)2+k
复习导入
如何求二次函数的表达式?
探究新知
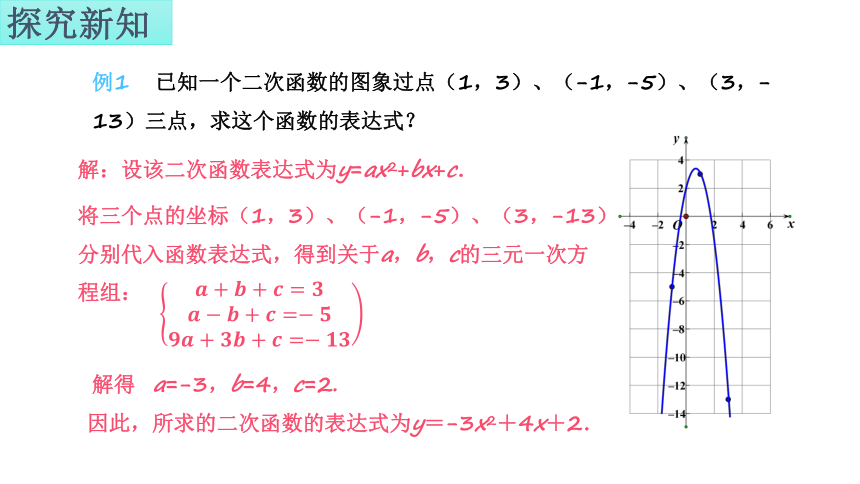
例1 已知一个二次函数的图象过点(1,3)、(-1,-5)、(3,-13)三点,求这个函数的表达式?
解:设该二次函数表达式为y=ax2+bx+c.
将三个点的坐标(1,3)、(-1,-5)、(3,-13)分别代入函数表达式,得到关于a,b,c的三元一次方程组:
解得 a=-3,b=4,c=2.
因此,所求的二次函数的表达式为y=-3x2+4x+2.
探究新知
例2 已知一个二次函数的图象过点(-1,0)、(3,0)、(1,-4)三点,求这个函数的表达式?
分析:二次函数的交点式:y=a(x-x1)(x-x2)(a≠0),给出三点,其中两点为函数图象与x轴的交点(x1,0),(x2,0)时可利用此式来求.
解:∵二次函数的图象过点(-1,0)、(3,0)
∴设该二次函数表达式为y=a(x+1)(x-3).
将(1,-4)代入函数表达式,可得:
-4=a(1+1)(1-3)
解得 a=1.
∴所求的二次函数的表达式为y=(x+1)(x-3),即 y=x2-2x-3 .
知识要点
已知三点求二次函数的解析式的一般步骤:
1.设:设二次函数的解析式为:y=ax2+bx+c或y=a(x-x1)(x-x2);
2.代:把三点的坐标代入所设的函数解析式;
3.解:解方程(组);
4.写:回代解析式,写成一般形式.
那么如何判断三个点是否在一条直线上?
求经过其中两个点的直线表达式,再判断第三个点是否适合这个表达式.
典例精析
例3 已知三个点的坐标,是否有一个二次函数,它的图象经过这三个点?
(1)P(1,-5),Q(-1,3),R(2,-3);
(2)P(1,-5),Q(-1,3),M(2,-9).
典例精析
(1)P(1,-5),Q(-1,3),R(2,-3)
解:设有二次函数y=ax2+bx+c,它的图象经过点P,Q,R三点,则得到关于a,b,c的三元一次方程组:
解得 a=2,b=-4,c=-3.
因此,二次函数y=2x2-4x-3的图象经过P,Q,R三点.
典例精析
(2)P(1,-5),Q(-1,3),M(2,-9)
解:设有二次函数y=ax2+bx+c,它的图象经过点P,Q,M三点,则得到关于a,b,c的三元一次方程组:
解得 a=0,b=-4,c=-1.
因此,一次函数y=-4x-1的图象经过P,Q,M三点.这说明没有这样的二次函数,它的图象能经过P,Q,M三点.
y = - 4x – 1
例2中:两点P(1, -5), Q(-1, 3)确定了一个一次函数 y = - 4x - 1 .
点 R(2, -3)的坐标不适合 y = - 4x - 1 , 因此点 R 不在直线 PQ 上,即P, Q, R 三点不共线.
点 M(2, -9)的坐标适合 y = - 4x - 1,因此点 M在直线 PQ 上,即 P,Q,M 三点共线.
典例精析
如何判断三个点是否在一条直线上?
求经过其中两个点的直线表达式,再判断第三个点是否适合这个表达式.
知识要点
通过例2的解答你可以得到什么结论?
1、二次函数y=ax2+bx+c的图象上任意三个不同的点都不在一条直线上.
2、若给定不共线三点的坐标,且它们的横坐标两两不等,则可以确定唯一的一个二次函数,它的图象经过这三点.
典例精析
例3 选取顶点(-2,1)和点(1,-8),试求出这个二次函数的表达式。
解:设这个二次函数的表达式是y=a(x-h)2+k,
把顶点(-2,1)代入y=a(x-h)2+k得
y=a(x+2)2+1
再把点(1,-8)代入上式得
a(1-h)2+1=-8,
解得a=-1
因此,所求的二次函数的表达式为y=-(x+2)2+1或y=-x2-4x-3
知识要点
通过例3的解答你可以得到什么结论?
1.若已知抛物线的顶点坐标和抛物线上的另一个点的坐标时,通常设函数的解析式为y=a(x-h)2+k。
2.特别地,当抛物线的顶点为原点时,h=0,k=0,可设函数的解析式为y=ax2。
3.当抛物线的对称轴为y轴时,h=0,可设函数的解析式为y=ax2+k。
4.当抛物线的对称轴为x轴时,k=0,可设函数的解析式为y=a(x-h)2。
当堂练习
1.已知二次函数的图象经过点(0,3)、(-3,0)、(2,-5)
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
解:(1)设此二次函数的解析式为y=ax2+bx+c,
将(0,3)、(-3,0)、(2,-5)代入y=ax2+bx+c,
解得 a=-1,b=-2,c=3.
∴此二次函数的解析式是y=-x2-2x+3.
(2)当x=-2时,y=-(-2)2-2×(-2)+3=3,
∴点P(-2,3)在此二次函数的图象上.
当堂练习
2. 若抛物线经过点 (3, 0)和(2, -3), 且以直线 x =1为对称轴,
则该抛物线的表达式为( )
A.y=-x2-2x-3 B.y=x2-2x+3
C.y=x2-2x-3 D.y=-x2+2x-3
C
3. 抛物线 y= ax2+bx+c 与 x 轴的两个交点分别为(-1, 0),
(3, 0),其形状和开口方向与抛物线 y=-2x2 相同,则抛物线
y=ax2+bx+c 的表达式为( )
A.y=-2x2-x+3
B.y=-2x2+4x+5
C.y=-2x2+4x+8
D.y=-2x2+4x+6
D
3.(分类讨论题)已知抛物线过点 A(2,0),B(-1,0),与 y 轴交于点 C, 且 OC =2, 则这条抛物线的表达式为( )
A.y=x2-x-2
B.y=-x2+x+2
C.y=x2-x-2 或 y=-x2+x+2
D.y=-x2-x-2 或 y=x2+x+2
C
4. 已知抛物线 y=-x2+bx+c 如图所示, 则此抛物线
的表达式为_________________.
y =-x2+2x+3
当堂练习
课堂小结
求二次函数解析式的三种表达式的形式.
(1)已知三点坐标,设二次函数解析式为 y = ax2+bx+c.
(2)已知顶点坐标:设二次函数解析式为 y=a(x-h)2+k.
(3)已知抛物线与 x 轴两交点坐标为(x1,0),(x2,0)可设二次函数解析式为 y = a(x-x1)(x-x2).
如何判断三个点是否在一条直线上?
求经过其中两个点的直线表达式,再判断第三个点是否适合这个表达式.
第一章 二次函数
1.3 不共线三点确定二次函数的表达式
复习导入
y=ax2+bx+c
对称轴是:
顶点坐标是:
当 时,函数达到最大值(当a<0)或最小值(当a>0): .
复习导入
二次函数y=ax2+bx+c的性质:
y=ax2+bx+c 开口 方向 对称轴 顶点坐标 最大(小)值 增减性
a>0
a<0
向上
向下
时,y随x的增大而减小, 时,y随x的增大而增大.
时,y随x的增大而增大, 时,y随x的增大而减小.
1、怎样用待定系数法确定一次函数的解析式?
y=kx+b (k≠0)
系数k,
b待定
找两个点
确定两个方程
解二元一次方程组
2、二次函数的表达式有哪些?
一般式: y=ax2+bx+c
顶点式: y=a(x-h)2+k
复习导入
如何求二次函数的表达式?
探究新知
例1 已知一个二次函数的图象过点(1,3)、(-1,-5)、(3,-13)三点,求这个函数的表达式?
解:设该二次函数表达式为y=ax2+bx+c.
将三个点的坐标(1,3)、(-1,-5)、(3,-13)分别代入函数表达式,得到关于a,b,c的三元一次方程组:
解得 a=-3,b=4,c=2.
因此,所求的二次函数的表达式为y=-3x2+4x+2.
探究新知
例2 已知一个二次函数的图象过点(-1,0)、(3,0)、(1,-4)三点,求这个函数的表达式?
分析:二次函数的交点式:y=a(x-x1)(x-x2)(a≠0),给出三点,其中两点为函数图象与x轴的交点(x1,0),(x2,0)时可利用此式来求.
解:∵二次函数的图象过点(-1,0)、(3,0)
∴设该二次函数表达式为y=a(x+1)(x-3).
将(1,-4)代入函数表达式,可得:
-4=a(1+1)(1-3)
解得 a=1.
∴所求的二次函数的表达式为y=(x+1)(x-3),即 y=x2-2x-3 .
知识要点
已知三点求二次函数的解析式的一般步骤:
1.设:设二次函数的解析式为:y=ax2+bx+c或y=a(x-x1)(x-x2);
2.代:把三点的坐标代入所设的函数解析式;
3.解:解方程(组);
4.写:回代解析式,写成一般形式.
那么如何判断三个点是否在一条直线上?
求经过其中两个点的直线表达式,再判断第三个点是否适合这个表达式.
典例精析
例3 已知三个点的坐标,是否有一个二次函数,它的图象经过这三个点?
(1)P(1,-5),Q(-1,3),R(2,-3);
(2)P(1,-5),Q(-1,3),M(2,-9).
典例精析
(1)P(1,-5),Q(-1,3),R(2,-3)
解:设有二次函数y=ax2+bx+c,它的图象经过点P,Q,R三点,则得到关于a,b,c的三元一次方程组:
解得 a=2,b=-4,c=-3.
因此,二次函数y=2x2-4x-3的图象经过P,Q,R三点.
典例精析
(2)P(1,-5),Q(-1,3),M(2,-9)
解:设有二次函数y=ax2+bx+c,它的图象经过点P,Q,M三点,则得到关于a,b,c的三元一次方程组:
解得 a=0,b=-4,c=-1.
因此,一次函数y=-4x-1的图象经过P,Q,M三点.这说明没有这样的二次函数,它的图象能经过P,Q,M三点.
y = - 4x – 1
例2中:两点P(1, -5), Q(-1, 3)确定了一个一次函数 y = - 4x - 1 .
点 R(2, -3)的坐标不适合 y = - 4x - 1 , 因此点 R 不在直线 PQ 上,即P, Q, R 三点不共线.
点 M(2, -9)的坐标适合 y = - 4x - 1,因此点 M在直线 PQ 上,即 P,Q,M 三点共线.
典例精析
如何判断三个点是否在一条直线上?
求经过其中两个点的直线表达式,再判断第三个点是否适合这个表达式.
知识要点
通过例2的解答你可以得到什么结论?
1、二次函数y=ax2+bx+c的图象上任意三个不同的点都不在一条直线上.
2、若给定不共线三点的坐标,且它们的横坐标两两不等,则可以确定唯一的一个二次函数,它的图象经过这三点.
典例精析
例3 选取顶点(-2,1)和点(1,-8),试求出这个二次函数的表达式。
解:设这个二次函数的表达式是y=a(x-h)2+k,
把顶点(-2,1)代入y=a(x-h)2+k得
y=a(x+2)2+1
再把点(1,-8)代入上式得
a(1-h)2+1=-8,
解得a=-1
因此,所求的二次函数的表达式为y=-(x+2)2+1或y=-x2-4x-3
知识要点
通过例3的解答你可以得到什么结论?
1.若已知抛物线的顶点坐标和抛物线上的另一个点的坐标时,通常设函数的解析式为y=a(x-h)2+k。
2.特别地,当抛物线的顶点为原点时,h=0,k=0,可设函数的解析式为y=ax2。
3.当抛物线的对称轴为y轴时,h=0,可设函数的解析式为y=ax2+k。
4.当抛物线的对称轴为x轴时,k=0,可设函数的解析式为y=a(x-h)2。
当堂练习
1.已知二次函数的图象经过点(0,3)、(-3,0)、(2,-5)
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
解:(1)设此二次函数的解析式为y=ax2+bx+c,
将(0,3)、(-3,0)、(2,-5)代入y=ax2+bx+c,
解得 a=-1,b=-2,c=3.
∴此二次函数的解析式是y=-x2-2x+3.
(2)当x=-2时,y=-(-2)2-2×(-2)+3=3,
∴点P(-2,3)在此二次函数的图象上.
当堂练习
2. 若抛物线经过点 (3, 0)和(2, -3), 且以直线 x =1为对称轴,
则该抛物线的表达式为( )
A.y=-x2-2x-3 B.y=x2-2x+3
C.y=x2-2x-3 D.y=-x2+2x-3
C
3. 抛物线 y= ax2+bx+c 与 x 轴的两个交点分别为(-1, 0),
(3, 0),其形状和开口方向与抛物线 y=-2x2 相同,则抛物线
y=ax2+bx+c 的表达式为( )
A.y=-2x2-x+3
B.y=-2x2+4x+5
C.y=-2x2+4x+8
D.y=-2x2+4x+6
D
3.(分类讨论题)已知抛物线过点 A(2,0),B(-1,0),与 y 轴交于点 C, 且 OC =2, 则这条抛物线的表达式为( )
A.y=x2-x-2
B.y=-x2+x+2
C.y=x2-x-2 或 y=-x2+x+2
D.y=-x2-x-2 或 y=x2+x+2
C
4. 已知抛物线 y=-x2+bx+c 如图所示, 则此抛物线
的表达式为_________________.
y =-x2+2x+3
当堂练习
课堂小结
求二次函数解析式的三种表达式的形式.
(1)已知三点坐标,设二次函数解析式为 y = ax2+bx+c.
(2)已知顶点坐标:设二次函数解析式为 y=a(x-h)2+k.
(3)已知抛物线与 x 轴两交点坐标为(x1,0),(x2,0)可设二次函数解析式为 y = a(x-x1)(x-x2).
如何判断三个点是否在一条直线上?
求经过其中两个点的直线表达式,再判断第三个点是否适合这个表达式.
