人教版八年级下册 第十九章 一次函数 19.2一次函数的定义(课件)(21张PPT)
文档属性
| 名称 | 人教版八年级下册 第十九章 一次函数 19.2一次函数的定义(课件)(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 378.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 18:06:26 | ||
图片预览








文档简介
(共21张PPT)
欢迎进入数学课堂
19.2.2.1 一次函数的定义
19.2 一次函数
情境导学
思考:假设故事中,瓶子为圆柱形,每个石子体积相同,瓶里原有水深 5 cm,放一粒石子水位上升 0.3 cm,那么放 x 粒石子后,水瓶的水深 y cm怎样表示呢?
y = 0.3x+5
它是正比例函数吗?
1、理解一次函数的定义
2、掌握一次函数与正比例函数的关系
3、能运用一次函数的相关知识解决实际问题
学习目标
下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式,这些函数解析式有哪些共同特征?
(1)有人发现,在20 ℃~25 ℃时蟋蟀每分鸣叫次数c 与温度 t(单位:℃)有关,且 c 的值约是 t 的7 倍与35的差;
(2)一种计算成年人标准体重G(单位:kg)的方法是,以厘米为单位量出身高值 h ,再减常数105,所得差是G 的值;
(3)某城市的市内电话的月收费额 y(单位:元)包括月租费22元和拨打电话 x min 的计时费(按0.1元/min收取);
(4)把一个长10 cm,宽5 cm的矩形的长减少 x cm, 宽不变,矩形面积 y(单位:cm2)随x的值而变化.
自主探究
(2)G=h-105
(3)y=0.1x+22
(4)y=-5x+50(0≤x<10)
(1)C=7t-35(20≤t≤25)
共同特征:
上面这些函数都是常数k与自变量的积与
常数b的和的形式。
合作探究
这些函数解析式有哪些共同特征?
(k、b为常数,且k≠0)
+b
k
(k、b为常数,且k≠0)
+b
k
=
一次函数的定义:
一般地,形如y=kx+b(k、b是常数,且k≠0)的函数,叫做一次函数。
1
函数
y
自变量
x
b为常数
b
(k 为常数,且k≠0)
k
学以致用
下列函数关系式中,哪些是一次函数,并说出k和b的值分别是多少?
(1) y= -3x+4
(2) y= -2x-5
(3) y= x2
(4)y=2x2+6
(5)
提示:先判断自变量x的最高次数是否为1,再判断一般形式为y=kx+b(k≠0)。
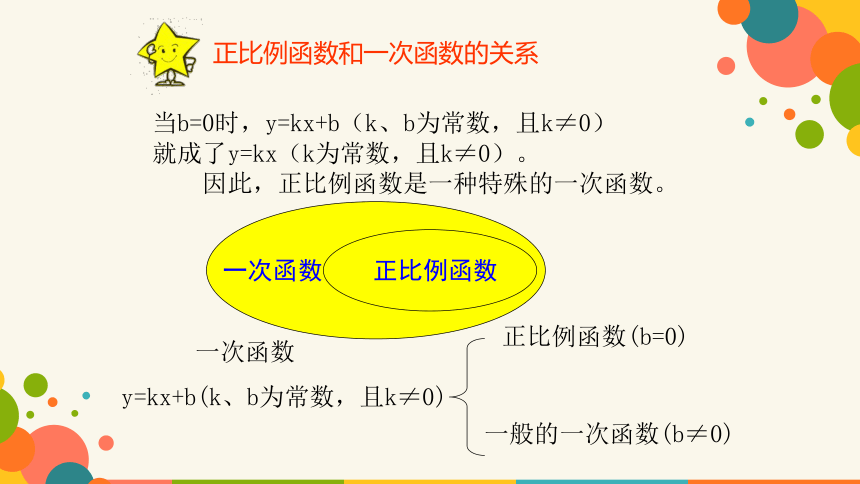
正比例函数和一次函数的关系
当b=0时,y=kx+b(k、b为常数,且k≠0)
就成了y=kx(k为常数,且k≠0)。
因此,正比例函数是一种特殊的一次函数。
一次函数
y=kx+b(k、b为常数,且k≠0)
正比例函数(b=0)
一般的一次函数(b≠0)
一次函数
正比例函数
已知函数 ,
当k __________时,它是一次函数;
当k __________时,它是正比例函数.
y=(k-1)x+k2 -1
k≠1
k=-1
学以致用
你已进入闯关大阵营
大家准备好了吗?
下列说法不正确的是( )
(A)一次函数不一定是正比例函数
(B)不是一次函数就一定不是正比例函数
(C)正比例函数是特定的一次函数
(D)不是正比例函数就不是一次函数
D
第一关
下列函数关系式中,哪些是一次函数,哪些又是正比例函数?
(1) y= -8x
(3)y=5x2+6
(2)
(4)y=-0.5x-1
解:_____________是一次函数,
___________是正比例函数。
(1)、(4)
(1)
第二关
下列函数中,是一次函数但不是正比例函数的是( )
(A) y= 2x
(B)
(C) y= 3.5-2x
(D)y=2x2-1
C
第三关
要使函数 是
一次函数,应满足( )
y=(m-2)xn-1+n
(A) m≠2,n≠2
(B) m=2,n=2
(C) m≠2,n=2
(D) m=2,n=0
C
第四关
1、已知函数y=(2-m)x+2m-3.求当m为何值时,
(1)此函数为一次函数;
(2) 此函数为正比例函数。
解:(1)由题意得, k = 2-m≠0, m≠2,所以m≠2时,此函数为一次函数。
(2)由题意, k = 2-m≠0, 解得,m≠2,
又因为b = 2m-3= 0, 解得,m=
所以当 m= 时,函数为正比例函数y= x。
第五关
已知一次函数y=kx+b ,
当x=1时y=5; x=-1时y=1. 求k、b的值.
解: 由题意得,
k+b=5
-k+b=1 ,
解得
k=2
b=3 .
第六关
写出下列各题中x和y之间的关系式,并并判断y是否是x的一次函数?是否为正比例函数?
(1)汽车以60千米/时的速度匀速行驶,行驶路程中y(千米)与行驶时间x(时)之间的关系式:
(2)一棵树现在高50厘米,每个月长高2厘米,x个月后这棵树的高度为y(厘米):
解:(1)函数关系式为:y=60x
它是正比例函数,也是一次函数。
(2)函数关系式为:y=2x+50
它是一次函数,不是正比例函数
第七关
1.一次函数的概念
2.一次函数与正比例函数的区别与联系
3.你的疑惑?
你的启示。
一般地,形如y=kx+b
(k、b为常数,k≠0)的函数,
叫做一次函数.
当b=0时,y=kx+b(k、b为常数,且k≠0)
就成了y=kx(k为常数,且k≠0)。
因此,正比例函数是一种特殊的一次函数。
畅所欲言
课堂总结
成功
天资
环境
勤奋和方法
作业
请同学们举出 一个一次函数的实际问题的例子和同桌交流,
然后写出其一次项系数k和常数项b的值。
欢迎进入数学课堂
19.2.2.1 一次函数的定义
19.2 一次函数
情境导学
思考:假设故事中,瓶子为圆柱形,每个石子体积相同,瓶里原有水深 5 cm,放一粒石子水位上升 0.3 cm,那么放 x 粒石子后,水瓶的水深 y cm怎样表示呢?
y = 0.3x+5
它是正比例函数吗?
1、理解一次函数的定义
2、掌握一次函数与正比例函数的关系
3、能运用一次函数的相关知识解决实际问题
学习目标
下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式,这些函数解析式有哪些共同特征?
(1)有人发现,在20 ℃~25 ℃时蟋蟀每分鸣叫次数c 与温度 t(单位:℃)有关,且 c 的值约是 t 的7 倍与35的差;
(2)一种计算成年人标准体重G(单位:kg)的方法是,以厘米为单位量出身高值 h ,再减常数105,所得差是G 的值;
(3)某城市的市内电话的月收费额 y(单位:元)包括月租费22元和拨打电话 x min 的计时费(按0.1元/min收取);
(4)把一个长10 cm,宽5 cm的矩形的长减少 x cm, 宽不变,矩形面积 y(单位:cm2)随x的值而变化.
自主探究
(2)G=h-105
(3)y=0.1x+22
(4)y=-5x+50(0≤x<10)
(1)C=7t-35(20≤t≤25)
共同特征:
上面这些函数都是常数k与自变量的积与
常数b的和的形式。
合作探究
这些函数解析式有哪些共同特征?
(k、b为常数,且k≠0)
+b
k
(k、b为常数,且k≠0)
+b
k
=
一次函数的定义:
一般地,形如y=kx+b(k、b是常数,且k≠0)的函数,叫做一次函数。
1
函数
y
自变量
x
b为常数
b
(k 为常数,且k≠0)
k
学以致用
下列函数关系式中,哪些是一次函数,并说出k和b的值分别是多少?
(1) y= -3x+4
(2) y= -2x-5
(3) y= x2
(4)y=2x2+6
(5)
提示:先判断自变量x的最高次数是否为1,再判断一般形式为y=kx+b(k≠0)。
正比例函数和一次函数的关系
当b=0时,y=kx+b(k、b为常数,且k≠0)
就成了y=kx(k为常数,且k≠0)。
因此,正比例函数是一种特殊的一次函数。
一次函数
y=kx+b(k、b为常数,且k≠0)
正比例函数(b=0)
一般的一次函数(b≠0)
一次函数
正比例函数
已知函数 ,
当k __________时,它是一次函数;
当k __________时,它是正比例函数.
y=(k-1)x+k2 -1
k≠1
k=-1
学以致用
你已进入闯关大阵营
大家准备好了吗?
下列说法不正确的是( )
(A)一次函数不一定是正比例函数
(B)不是一次函数就一定不是正比例函数
(C)正比例函数是特定的一次函数
(D)不是正比例函数就不是一次函数
D
第一关
下列函数关系式中,哪些是一次函数,哪些又是正比例函数?
(1) y= -8x
(3)y=5x2+6
(2)
(4)y=-0.5x-1
解:_____________是一次函数,
___________是正比例函数。
(1)、(4)
(1)
第二关
下列函数中,是一次函数但不是正比例函数的是( )
(A) y= 2x
(B)
(C) y= 3.5-2x
(D)y=2x2-1
C
第三关
要使函数 是
一次函数,应满足( )
y=(m-2)xn-1+n
(A) m≠2,n≠2
(B) m=2,n=2
(C) m≠2,n=2
(D) m=2,n=0
C
第四关
1、已知函数y=(2-m)x+2m-3.求当m为何值时,
(1)此函数为一次函数;
(2) 此函数为正比例函数。
解:(1)由题意得, k = 2-m≠0, m≠2,所以m≠2时,此函数为一次函数。
(2)由题意, k = 2-m≠0, 解得,m≠2,
又因为b = 2m-3= 0, 解得,m=
所以当 m= 时,函数为正比例函数y= x。
第五关
已知一次函数y=kx+b ,
当x=1时y=5; x=-1时y=1. 求k、b的值.
解: 由题意得,
k+b=5
-k+b=1 ,
解得
k=2
b=3 .
第六关
写出下列各题中x和y之间的关系式,并并判断y是否是x的一次函数?是否为正比例函数?
(1)汽车以60千米/时的速度匀速行驶,行驶路程中y(千米)与行驶时间x(时)之间的关系式:
(2)一棵树现在高50厘米,每个月长高2厘米,x个月后这棵树的高度为y(厘米):
解:(1)函数关系式为:y=60x
它是正比例函数,也是一次函数。
(2)函数关系式为:y=2x+50
它是一次函数,不是正比例函数
第七关
1.一次函数的概念
2.一次函数与正比例函数的区别与联系
3.你的疑惑?
你的启示。
一般地,形如y=kx+b
(k、b为常数,k≠0)的函数,
叫做一次函数.
当b=0时,y=kx+b(k、b为常数,且k≠0)
就成了y=kx(k为常数,且k≠0)。
因此,正比例函数是一种特殊的一次函数。
畅所欲言
课堂总结
成功
天资
环境
勤奋和方法
作业
请同学们举出 一个一次函数的实际问题的例子和同桌交流,
然后写出其一次项系数k和常数项b的值。
