18.1.2平行四边形的判定课件
文档属性
| 名称 | 18.1.2平行四边形的判定课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 373.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-21 00:00:00 | ||
图片预览


文档简介
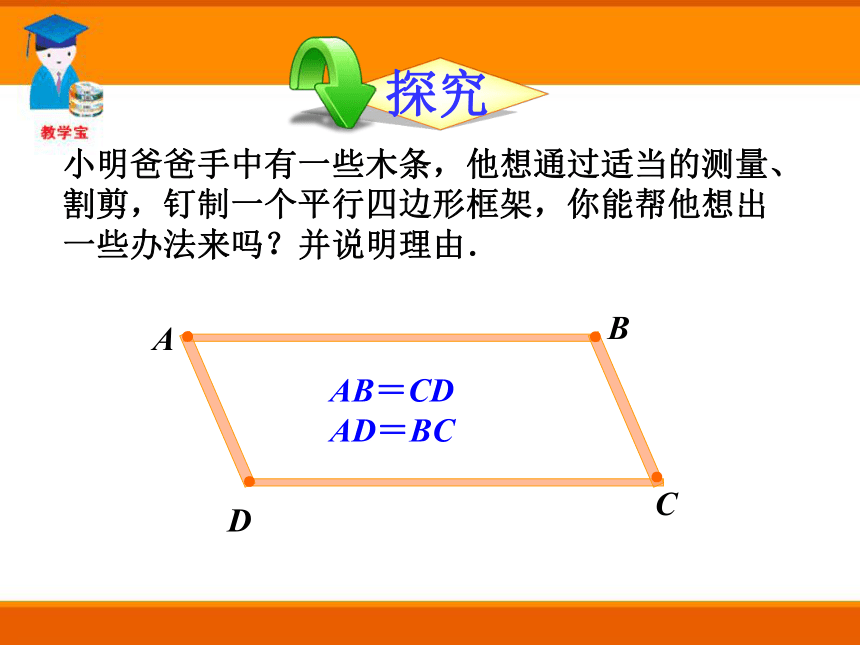
课件37张PPT。 下面图片中,哪些是平行四边形?你是怎样判断的?回顾旧知 平行四边形的判定小明爸爸手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗?并说明理由.●●●●ACBDAB=CD
AD=BC证明:连接AC.
∵ AB=CD,AD=BC,AC=AC
∴△ACD≌△CAD(SSS)
∴∠CAB=∠DCA
∴AB∥CD
同理,∠CAD=∠ACB
∴ AD∥BC
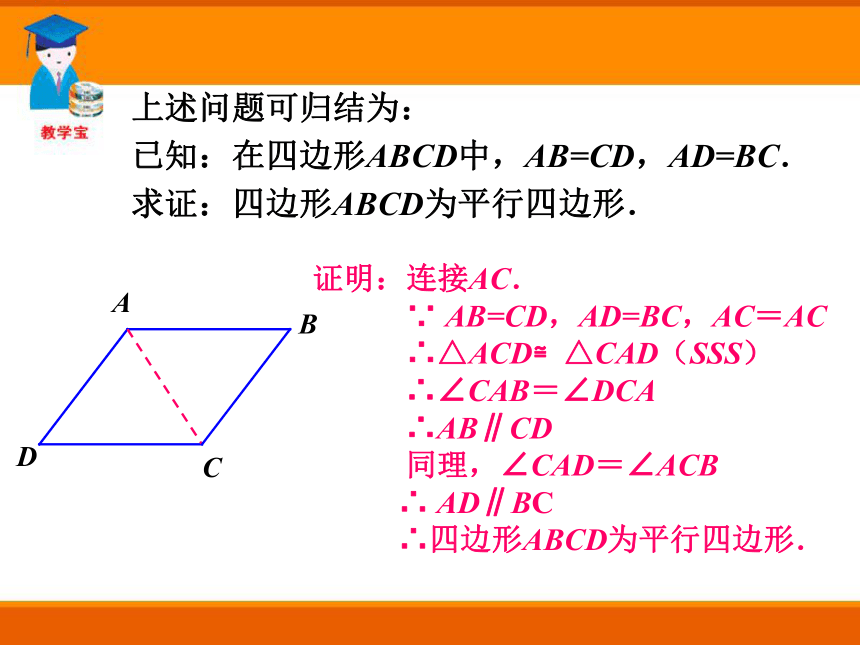
∴四边形ABCD为平行四边形.上述问题可归结为:
已知:在四边形ABCD中,AB=CD,AD=BC.
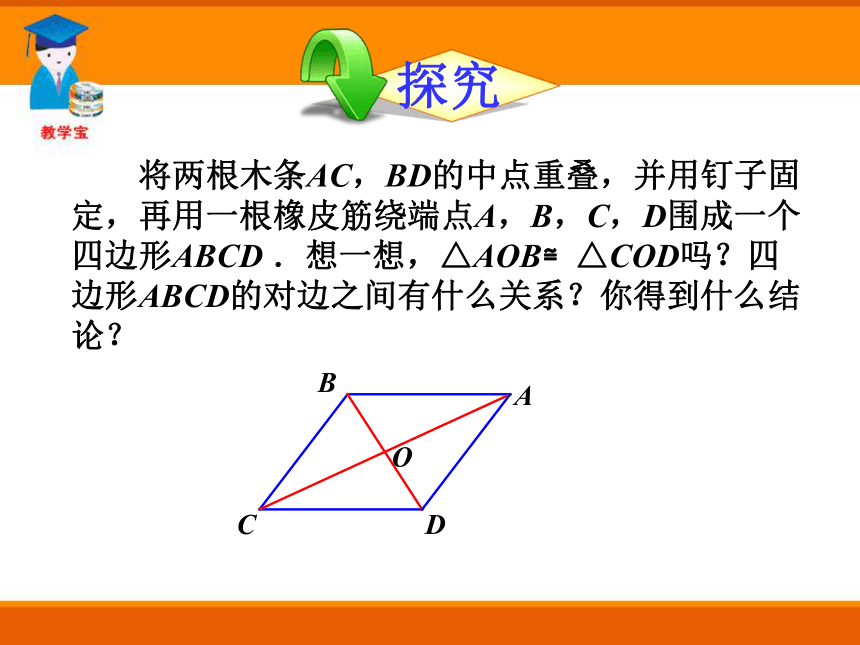
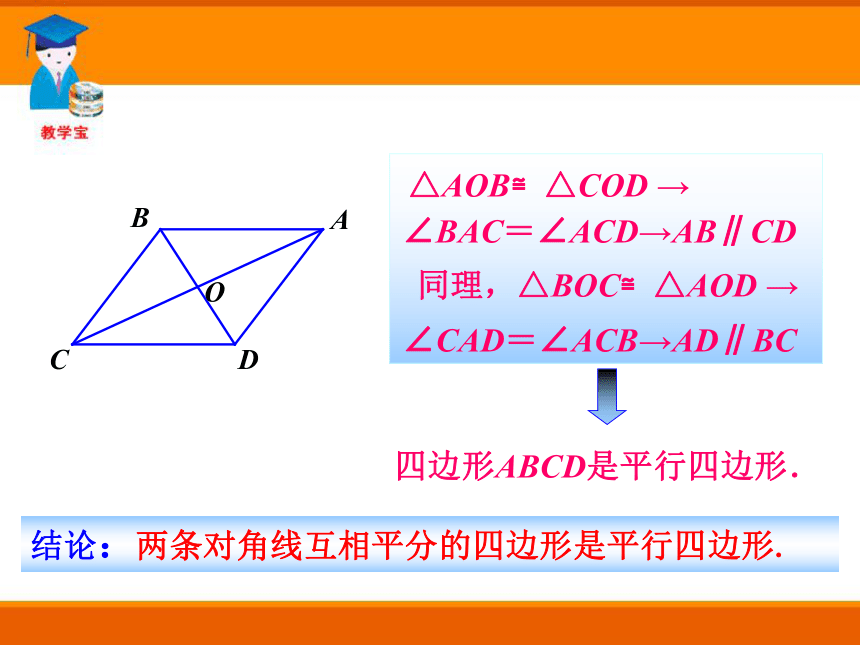
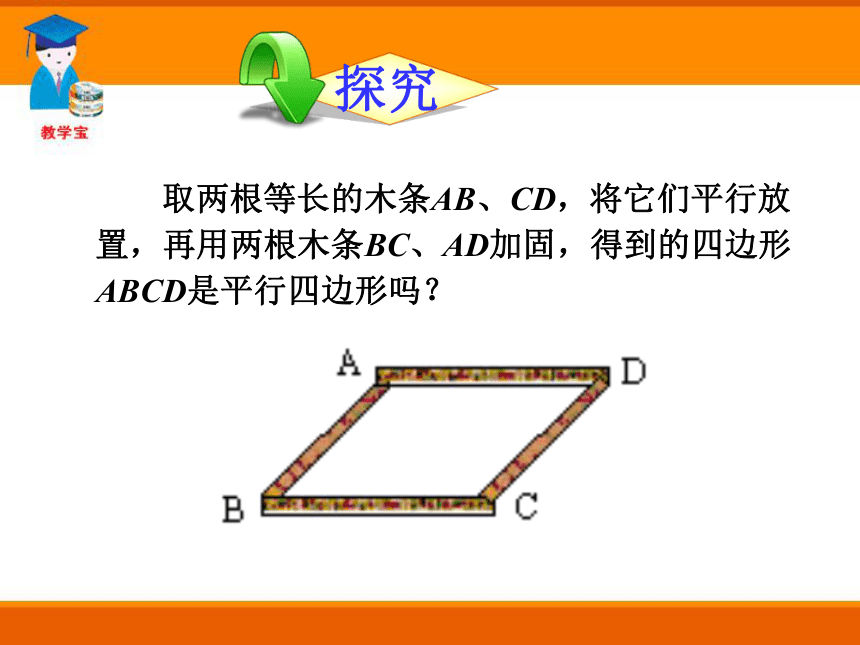
求证:四边形ABCD为平行四边形. 将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD .想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论? ACBOD△AOB≌△COD →∠BAC=∠ACD→AB∥CD∠CAD=∠ACB→AD∥BC同理,△BOC≌△AOD →四边形ABCD是平行四边形.结论:两条对角线互相平分的四边形是平行四边形. 取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?证明:连接AC
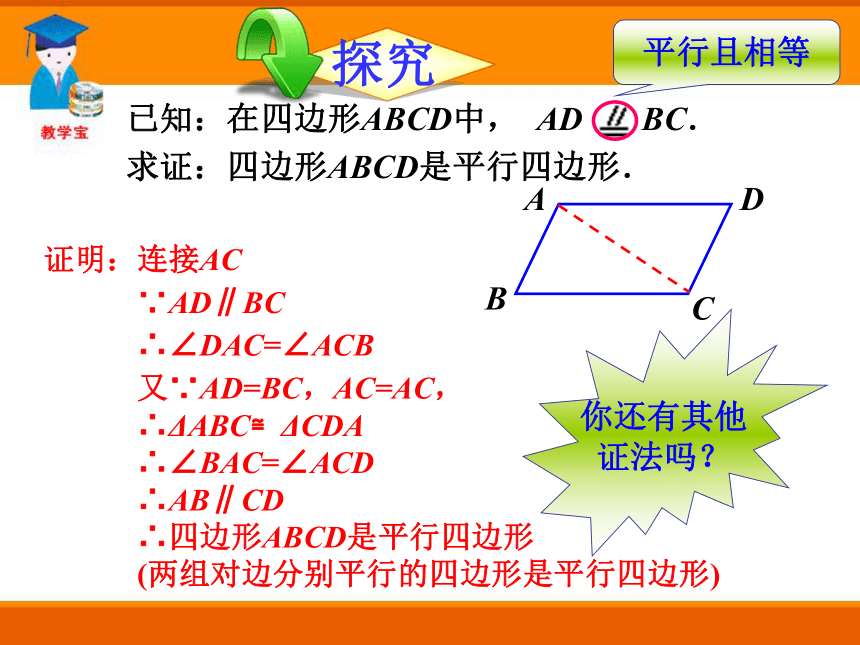
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)已知:在四边形ABCD中, AD BC.
求证:四边形ABCD是平行四边形. 平行且相等你还有其他
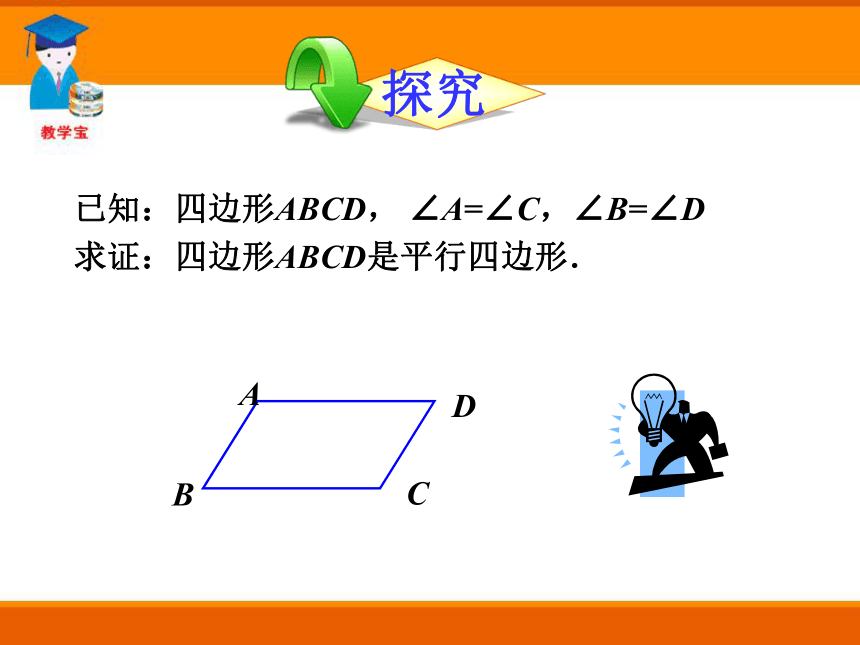
证法吗?已知:四边形ABCD, ∠A=∠C,∠B=∠D
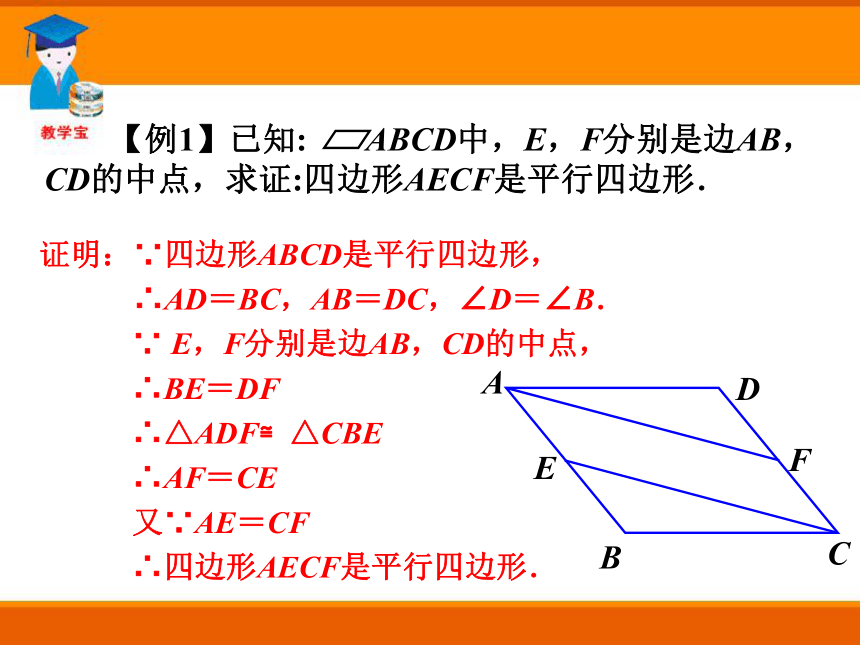
求证:四边形ABCD是平行四边形.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC,∠D=∠B.
∵ E,F分别是边AB,CD的中点,
∴BE=DF
∴△ADF≌△CBE
∴AF=CE
又∵AE=CF
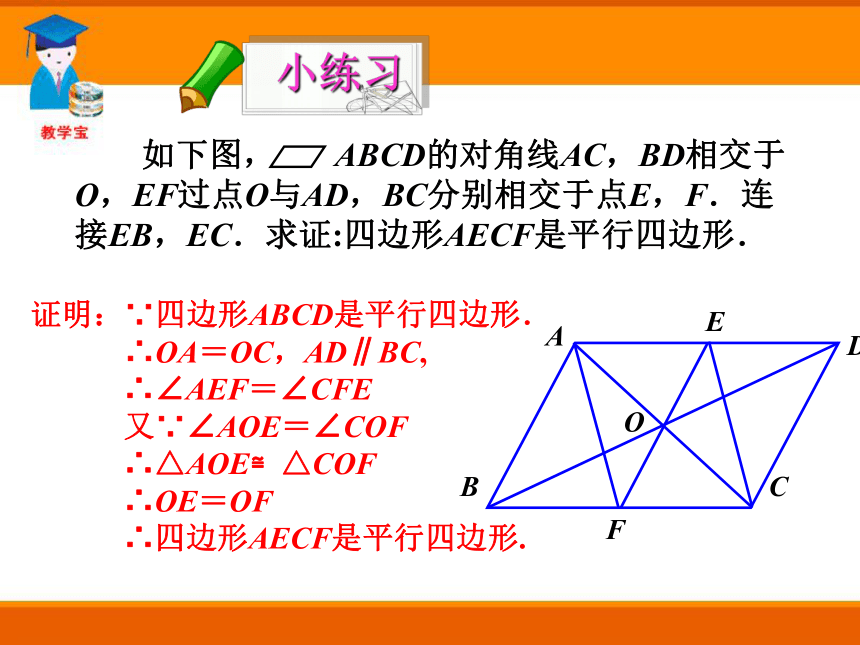
∴四边形AECF是平行四边形.小练习证明:∵四边形ABCD是平行四边形.
∴OA=OC,AD∥BC,
∴∠AEF=∠CFE
又∵∠AOE=∠COF
∴△AOE≌△COF
∴OE=OF
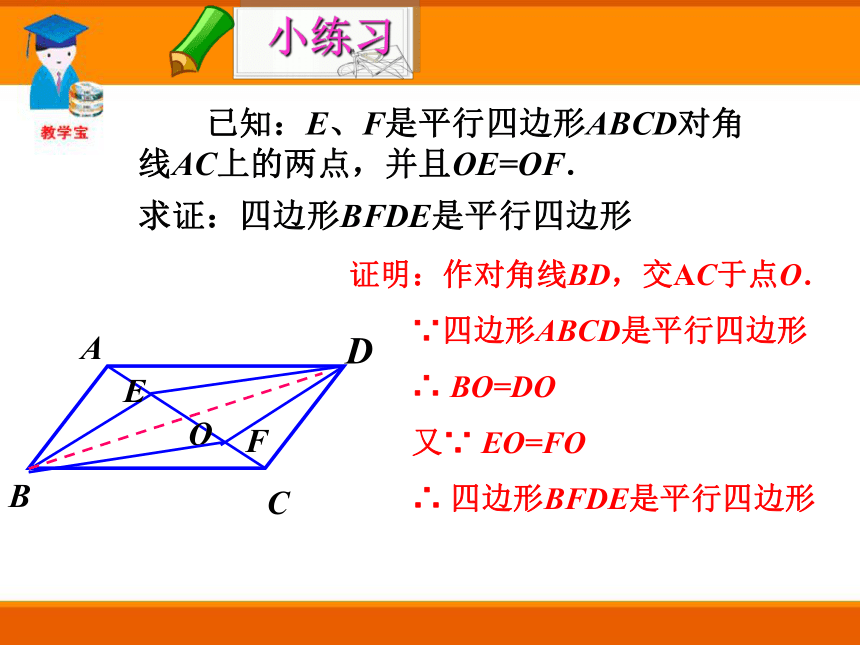
∴四边形AECF是平行四边形. 证明:作对角线BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ BO=DO
又∵ EO=FO
∴ 四边形BFDE是平行四边形 已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF.
求证:四边形BFDE是平行四边形DOABCEF小练习O ∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形证明:连接对角线BD,交AC于点O 【例2】已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.还有其他证明方法吗?AE=CF
∠EAD=∠FCB
AD=BC证明:∵四边形ABCD是平行四边形
∴AD ∥ BC且AD =BC
∴∠EAD=∠FCB
在△AED和△CFB中∴△AED ≌△CFB(SAS)
∴DE=BF
同理可证:BE=DF
四边形BFDE是平行四边形. 已知:E、F是平行四边形ABCD对角线AC上的两点,当点E,F满足什么条件时,四边形BFDE是平行四边形?已知:如图,A′B′∥BA,B′C′∥CB,
C′A′∥AC.
求证:
(1) ∠ABC=∠B′, ∠CAB=∠A′,
∠BCA=∠C′;
(2) △ABC的顶点分别是△B′C′A′各边的
中点.小练习证明:(1) ∵ A′B′∥BA,C′B′∥BC,
∴ 四边形ABCB′是平行四边形.
∴ ∠ABC=∠B′(平行四边形的对角相等).
同理∠CAB=∠A′,∠BCA=∠C′.
(2) 由(1)证得四边形ABCB′是平行四边形.同理,四边形ABA′C是平行四边形.
∴ AB=B′C, AB=A′C(平行四边形的对边相等).
∴ B′C=A′C.
同理 B′A=C′A, A′B=C′B.
∴ △ABC的顶点A、B、C分别是△B′C′A′的边B′C′、C′A′、A′B′的中点. 小明用手中六个全等的正三角形做拼图游戏时,拼成一个六边形.你能在图中找出所有的平行四边形吗?并说说你的理由. 解:有6个平行四边形,分别是:
ABOF, ABCO, BCDO,
CDEO, DEFO, EFAO.
理由是:因为正△ABO≌正△AOF,所以AB=BO,OF=FA.根据 “两组对边分别相等的四边形是平行四边形”,可知四边形ABCD是平行四边形.其它五个同理. 在一方格纸上,画一个有一组对边平行且相等的四边形. 步骤1:画一线段AD.
步骤2:平移线段AD到BC. 根据平移的特征,AD、BC有怎样的关系? 连结AB、DC,得到四边形ABCD,它是一组对边平行且相等的四边形CBDA 在 ABCD中,E、G是AD的三等分点,F、H是BC的三等分点,则图中的平行四边形有______个 . 抢答6 已知:如图, ABCD中,E、F分别是AD、BC的中点,求证:BE=DF.小练习证明:∵ 四边形ABCD是平行四边形,
∴ AD∥CB,AD=CD.
∵ E、F分别是AD、BC的中点,
∴ DE∥BF,且DE=AD,BF=BC.
∴ DE=BF.
∴ 四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
∴ BE=DF. 【例3】已知:如图, ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形. 证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,且AB∥CD.
∴ ∠BAE=∠DCF.
∵ BE⊥AC于E,DF⊥AC于F,
∴ BE∥DF,且∠BEA=∠DFC=90°.
∴ △ABE≌△CDF (AAS).
∴ BE=DF.
∴ 四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行) 已知:如图,AC∥ED,点B在AC上,且AB=ED=BC, 找出图中的平行四边形,并说明理由.四边形ABDE和四边形BCDE是平行四边形.
理由:一组对边平行且相等的四边形平行四边形.小练习已知:如图,在 ABCD中,AE、CF分别是
∠DAB、∠BCD的平分线.
求证:四边形AFCE是平行四边形.提示:利用“一组对边平行且相等的四边形平行四边形”.小练习平行四边形的判定方法从边来判定两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形1.下列四边形哪些是平行四边形?为什么?ADCB110°70°110°ABCD120°60°5㎝5㎝2.根据下列条件,不能判定一个四边形为平行
四边形的是( )
A.两组对边分别相等
B.两条对角线互相平分
C.两条对角线相等
D.两组对边分别平行C3.如图四边形ABCD中,AB//CD,只需添加
一个条件,能使四边形ABCD是平行四边
形,现有条件:①AB=CD,②BC=AD,
③AD//BC,④∠ABC=∠ADC,
这些条件中,满足要求的有( )
A.1个 B.2个 C.3个 D.4个C4.在下列条件中,不能判定四边形是平行四边形
的是( )
A.AB∥CD,AD∥BC
B. AB=CD,AD=BC
C.AB∥CD,AB=CD
D. AB∥CD,AD=BCDC5.如图,在 ABCD中,对角线AC,BD相交于点O,AC=10,BD=8,则AD长度的取值范围是 ( )
A.AD>1 B.AD<9
C.AD>10 D.1 BC、CA的中点,以这些点为顶点,你能在
图中画出多少个平行四边形?3个.7.(1)已知:平行四边形ABCD中,E、F分别
是边AD、BC的中点;求证:EB=DF. (2)在(1)的图中,AF交BE于G,CE交
DF于H;求证:EF与GH相互平分.提示:(1)由△ABE≌△CDF→ EB=DF.
(2)先证GE=FH
EH=GF四边形EGFH为平行四边形.
AD=BC证明:连接AC.
∵ AB=CD,AD=BC,AC=AC
∴△ACD≌△CAD(SSS)
∴∠CAB=∠DCA
∴AB∥CD
同理,∠CAD=∠ACB
∴ AD∥BC
∴四边形ABCD为平行四边形.上述问题可归结为:
已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD为平行四边形. 将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD .想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论? ACBOD△AOB≌△COD →∠BAC=∠ACD→AB∥CD∠CAD=∠ACB→AD∥BC同理,△BOC≌△AOD →四边形ABCD是平行四边形.结论:两条对角线互相平分的四边形是平行四边形. 取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)已知:在四边形ABCD中, AD BC.
求证:四边形ABCD是平行四边形. 平行且相等你还有其他
证法吗?已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC,∠D=∠B.
∵ E,F分别是边AB,CD的中点,
∴BE=DF
∴△ADF≌△CBE
∴AF=CE
又∵AE=CF
∴四边形AECF是平行四边形.小练习证明:∵四边形ABCD是平行四边形.
∴OA=OC,AD∥BC,
∴∠AEF=∠CFE
又∵∠AOE=∠COF
∴△AOE≌△COF
∴OE=OF
∴四边形AECF是平行四边形. 证明:作对角线BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ BO=DO
又∵ EO=FO
∴ 四边形BFDE是平行四边形 已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF.
求证:四边形BFDE是平行四边形DOABCEF小练习O ∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形证明:连接对角线BD,交AC于点O 【例2】已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.还有其他证明方法吗?AE=CF
∠EAD=∠FCB
AD=BC证明:∵四边形ABCD是平行四边形
∴AD ∥ BC且AD =BC
∴∠EAD=∠FCB
在△AED和△CFB中∴△AED ≌△CFB(SAS)
∴DE=BF
同理可证:BE=DF
四边形BFDE是平行四边形. 已知:E、F是平行四边形ABCD对角线AC上的两点,当点E,F满足什么条件时,四边形BFDE是平行四边形?已知:如图,A′B′∥BA,B′C′∥CB,
C′A′∥AC.
求证:
(1) ∠ABC=∠B′, ∠CAB=∠A′,
∠BCA=∠C′;
(2) △ABC的顶点分别是△B′C′A′各边的
中点.小练习证明:(1) ∵ A′B′∥BA,C′B′∥BC,
∴ 四边形ABCB′是平行四边形.
∴ ∠ABC=∠B′(平行四边形的对角相等).
同理∠CAB=∠A′,∠BCA=∠C′.
(2) 由(1)证得四边形ABCB′是平行四边形.同理,四边形ABA′C是平行四边形.
∴ AB=B′C, AB=A′C(平行四边形的对边相等).
∴ B′C=A′C.
同理 B′A=C′A, A′B=C′B.
∴ △ABC的顶点A、B、C分别是△B′C′A′的边B′C′、C′A′、A′B′的中点. 小明用手中六个全等的正三角形做拼图游戏时,拼成一个六边形.你能在图中找出所有的平行四边形吗?并说说你的理由. 解:有6个平行四边形,分别是:
ABOF, ABCO, BCDO,
CDEO, DEFO, EFAO.
理由是:因为正△ABO≌正△AOF,所以AB=BO,OF=FA.根据 “两组对边分别相等的四边形是平行四边形”,可知四边形ABCD是平行四边形.其它五个同理. 在一方格纸上,画一个有一组对边平行且相等的四边形. 步骤1:画一线段AD.
步骤2:平移线段AD到BC. 根据平移的特征,AD、BC有怎样的关系? 连结AB、DC,得到四边形ABCD,它是一组对边平行且相等的四边形CBDA 在 ABCD中,E、G是AD的三等分点,F、H是BC的三等分点,则图中的平行四边形有______个 . 抢答6 已知:如图, ABCD中,E、F分别是AD、BC的中点,求证:BE=DF.小练习证明:∵ 四边形ABCD是平行四边形,
∴ AD∥CB,AD=CD.
∵ E、F分别是AD、BC的中点,
∴ DE∥BF,且DE=AD,BF=BC.
∴ DE=BF.
∴ 四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
∴ BE=DF. 【例3】已知:如图, ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形. 证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,且AB∥CD.
∴ ∠BAE=∠DCF.
∵ BE⊥AC于E,DF⊥AC于F,
∴ BE∥DF,且∠BEA=∠DFC=90°.
∴ △ABE≌△CDF (AAS).
∴ BE=DF.
∴ 四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行) 已知:如图,AC∥ED,点B在AC上,且AB=ED=BC, 找出图中的平行四边形,并说明理由.四边形ABDE和四边形BCDE是平行四边形.
理由:一组对边平行且相等的四边形平行四边形.小练习已知:如图,在 ABCD中,AE、CF分别是
∠DAB、∠BCD的平分线.
求证:四边形AFCE是平行四边形.提示:利用“一组对边平行且相等的四边形平行四边形”.小练习平行四边形的判定方法从边来判定两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形1.下列四边形哪些是平行四边形?为什么?ADCB110°70°110°ABCD120°60°5㎝5㎝2.根据下列条件,不能判定一个四边形为平行
四边形的是( )
A.两组对边分别相等
B.两条对角线互相平分
C.两条对角线相等
D.两组对边分别平行C3.如图四边形ABCD中,AB//CD,只需添加
一个条件,能使四边形ABCD是平行四边
形,现有条件:①AB=CD,②BC=AD,
③AD//BC,④∠ABC=∠ADC,
这些条件中,满足要求的有( )
A.1个 B.2个 C.3个 D.4个C4.在下列条件中,不能判定四边形是平行四边形
的是( )
A.AB∥CD,AD∥BC
B. AB=CD,AD=BC
C.AB∥CD,AB=CD
D. AB∥CD,AD=BCDC5.如图,在 ABCD中,对角线AC,BD相交于点O,AC=10,BD=8,则AD长度的取值范围是 ( )
A.AD>1 B.AD<9
C.AD>10 D.1
图中画出多少个平行四边形?3个.7.(1)已知:平行四边形ABCD中,E、F分别
是边AD、BC的中点;求证:EB=DF. (2)在(1)的图中,AF交BE于G,CE交
DF于H;求证:EF与GH相互平分.提示:(1)由△ABE≌△CDF→ EB=DF.
(2)先证GE=FH
EH=GF四边形EGFH为平行四边形.
