2.2 整式的加减 (第1课时)课件 40张PPT 2023-2024学年人教版七年级上
文档属性
| 名称 | 2.2 整式的加减 (第1课时)课件 40张PPT 2023-2024学年人教版七年级上 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 18:59:35 | ||
图片预览









文档简介
(共40张PPT)
第二章 整式的加减
2.2 整式的加减 第1课时
1.通过实例理解同类项的定义;
一、学习目标
2.知道只有同类项之间才能进行加减运算,掌握合并同类项的方法;
3.学会将一个多项式进行升(降)幂排列;即按一个字母的次数的
大小规律排列.
二、新课导入
观察下列物品摆放
饮料摆放
水果摆放
思考:这些物品摆放有什么特点?
三、概念剖析
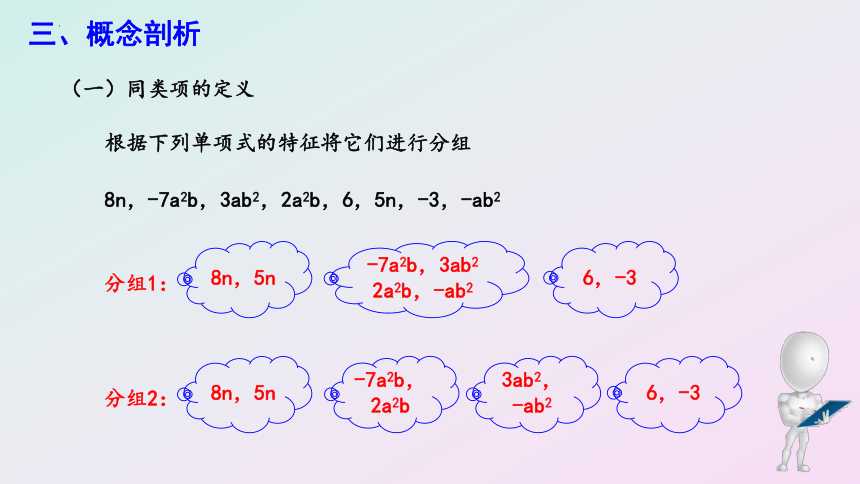
根据下列单项式的特征将它们进行分组
8n,-7a2b,3ab2,2a2b,6,5n,-3,-ab2
(一)同类项的定义
分组1:
8n,5n
6,-3
-7a2b,3ab2
2a2b,-ab2
分组2:
8n,5n
6,-3
-7a2b,2a2b
3ab2,
-ab2
三、概念剖析
所含字母相同,并且相同字母的指数也分别相同的项叫做同类项
例如上面分组中单项式5n和8n是同类项,-7a2b和2a2b是同类项;-7a2b
和3ab2不是同类项,因为它们字母的指数不相同.
所有的常数项也看做同类项
(一)同类项的定义
例如上面分组中单项式6和-3是同类项.
三、概念剖析
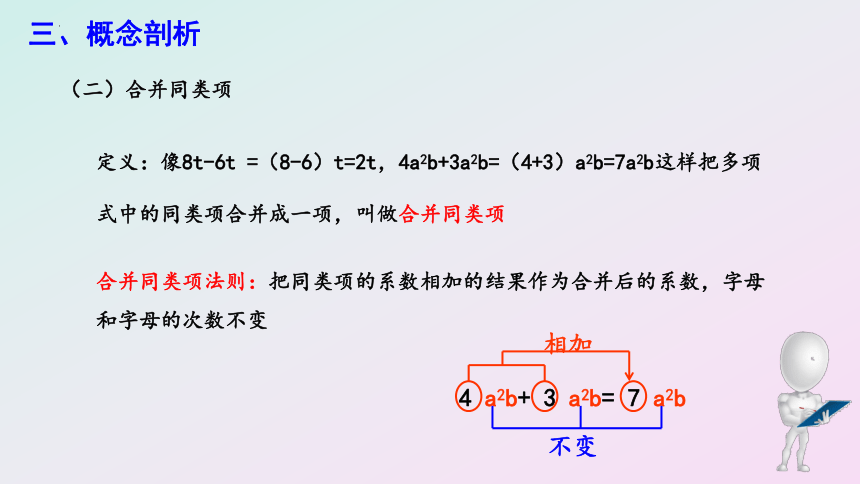
定义:像8t-6t =(8-6)t=2t,4a2b+3a2b=(4+3)a2b=7a2b这样把多项式中的同类项合并成一项,叫做合并同类项
合并同类项法则:把同类项的系数相加的结果作为合并后的系数,字母和字母的次数不变
(二)合并同类项
4 a2b+ 3 a2b= 7 a2b
相加
不变
三、概念剖析
把一个多项式按照某个字母指数从大到小排列,叫降幂排列.
(三)多项式的排列
如:a2 + a-1
注意:交换项的位置时,要连同项的符号一起交换!
把一个多项式按照某个字母指数从小到大排列,叫升幂排列.
如:-1+a+a2
四、典型例题
(一)同类项的定义
例1.下列的每组式子分别是同类项吗?
(1)2x2与-x2 (2)3a2b与3ab2
(3)4m2n3与2n3m2 (4)3π2a与-2a
(5)6与-0.5 (6)8s与11t
是
不是
是
是
是
不是
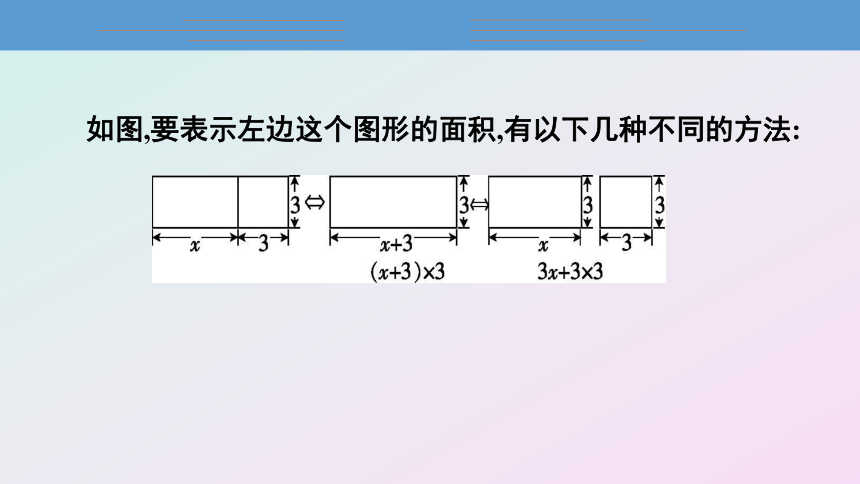
如图,要表示左边这个图形的面积,有以下几种不同的方法:
右边两个图中的图形面积是否相等呢 显然是相等的,于是我们可以得到一个等式:(x+3)×3=3x+3×3.
可见,代数式去括号法则与有理数的去括号法则是一样的.
阅读教材本课时所有内容,回答下列问题.
1.(1)如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号 ;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号 .
(2)括号前只有因数“+”或者“-”号的,可以分别看作数字因数是 或者 .
相反
整式去括号法则
-1
1
相同
化简下列各式.
(1)(5a+3b)-(3a-2b)
=5a+3b
= ;
-3a+2b
2a+5b
(2)2(4x-6y)-3(2x+3y-1)
=8x-12y
= .
-6x-9y+3
2x-21y+3
·导学建议·
去括号是整式运算中的基础运算,重点强调学生按照相应的步骤进行计算,先去括号,然后进行合并同类项.尤其注意括号外面有系数以及负号时,更要认真计算,避免前面变了号,后面就忘了变号.
·学习小助手·
对于有多重括号的整式,特别是括号外面还有负号的式子,在去括号的时候注意从里到外层层“脱落”,并注意遇到括号外面是负号的,每个式子都得变号.
去括号法则
1.下列去括号,正确的是 ( )
A.a2-(2a-1)=a2-2a-1
B.a2+(2a-3)=a2-2a+3
C.-(a+b)+(c-d)=-a-b-c+d
D.-(a+b)+(d-1)=-a-b+d-1
D
添括号
2.将多项式3x3-2x2+4x-5添括号后正确的是 ( )
A.3x3-(2x2+4x-5)
B.(3x3+4x)-(2x2+5)
C.(3x3-5)+(-2x2-4x)
D.2x2+(3x3+4x-5)
B
方法归纳交流 添括号法则:①所添括号前面是“+”号,括到括号里的各项都不变符号;②所添括号前面是“-”号,括到括号里的各项都改变符号.
变式演练 不改变x-(y-3z)的值,把括号前的“-”号变成“+”号,结果应是( )
A.x+(y-3z) B.x+(-y-3z)
C.x+(y+3z) D.x+(-y+3z)
D
3.先去括号,再合并同类项.
(1)6a+(4a-2b); (2)x-3(2x+5y-6).
解:(1)原式=10a-2b;
(2)原式=-5x-15y+18.
去括号合并同类项
变式演练 先化简,再求值:
解:原式=3a-2a2-(5a-2a2+3a-4a2)=3a-2a2-5a+2a2-3a+4a2=4a2-5a.
4.为资助贫困地区儿童入学,某校甲、乙、丙三位同学决定把平时节省下来的零花钱捐给希望工程.已知甲同学捐款x元,乙同学的捐款数比甲同学的3倍少6元,丙同学的捐款数是甲的2倍.
(1)甲、乙、丙的捐款总数是多少元
(2)当x=30时,甲、乙、丙共捐款多少元
解:(1)由题知乙同学捐款(3x-6)元,丙同学捐款2x元.所以甲、乙、丙三人共捐款:x+(3x-6)+2x=6x-6(元).
(2)当x=30时,原式=6×30-6=180-6=174(元).
用去括号法则解决实际问题
·导学建议·
本节课初步学习了用整式去括号法则解决实际问题,下一个课时将进一步学习用整式的加减运算解决代数问题与实际问题.
·学习小助手·
去括号与添括号一样,关注括号外面的符号,如果是正号,里面的符号都不变.如果是负号,里面的符号都改变,要养成及时检查的习惯.
1.当a=-1,b=2时,代数式3a+b+2(3a+b)+1的值为 ( )
A.-2 B.0
C.1 D.3
A
2.化简-[-(-a2)-b2]-[+(-b2)]的结果是 ( )
A.2b2-a2 B.-a2
C.a2 D.a2-2b2
3.多项式mx2-(1-x-6x2)化简后不含x的二次项,则m的值为 .
-6
A
四、典型例题
例2.已知3x2my3 和 -2x2yn 是同类项,则式子m+n的值是多少?
(一)同类项的定义
解:因为3x2my3 和 -2x2yn 是同类项,所以2m=2,3=n ,所以
m=1,n=3;则m+n=4.
总结:两个式子是否为同类项与系数无关,与字母顺序无关;几个
常数项也是同类项.
四、典型例题
【当堂检测】
1.判断下列各组是否是同类项,是打“√”,不是打“×”.
(1) 3x与 3mx ( ) (2) 2ab与 -5ab ( )
(3) 5ab2与 -2ab2c ( ) (4) 23与 32 ( )
√
×
×
√
【当堂检测】
2.若5x3yn和﹣xmy2是同类项,则3m﹣7n= .
-5
四、典型例题
(二)合并同类项
例3.合并下列各式的同类项
(1)-2a2b+3ab2-3a2b+2ab2 (2)3x2+5xy+y2-3x2-3xy
解:(1)原式=(-2-3)a2b+(3+2)ab2=-5a2b+5ab2
(2)原式=(3-3)x2+(5-3)xy+y2=2xy+y2
总结:合并同类项时:先找出多项式中的同类项;再利用加法的交换
律,将不同类的同类项集中到不同的括号内;最后将同一括号
内的同类项相加即可.
四、典型例题
【当堂检测】
3.x2y -πx+x3y2+3按照x指数进行升幂排列为 .
3-πx+x2y+x3y2
总结:进行降幂排列,交换项的位置时,要连同项的符号一起交换.
【当堂检测】
4.合并同类项:
解:原式=(2+1-2)a+(1-2)b
=a-b
解:原式=(3-5+3)a +(1-7)ab+(-1+7)b
=a -6ab+6b
例4.(1)求多项式2x2 -5x+x2 +4x-3x2 -2的值,其中x=1.
解:2x2-5x+x2+4x-3x2-2=(2+1-3)x2+(-5+4)x-2=-x-2
当x=1时,原式=-1-2=-3.
四、典型例题
(三)化简、求值
(2)化简、求值: 其中 .
解:
四、典型例题
当 时,
原式
【当堂检测】
5.当x=-1时,求-x +2x+x -x+1的值.
解:-x2+2x+x2-x+1
=-x2+x2+2x-x+1
=(-x2+x2)+(2x-x)+1
=x+1.
当x=-1时,原式=-1+1=0.
【当堂检测】
6.有一道题,求3a2-4a2b+3ab+4a2b-ab+a2-2ab的值,其中a=-1,b=6,小明同学把b=6错写成了b=9,但他计算的结果是正确的,请你通过计算说明这是怎么回事.
解:原式=4a2,当a=-1,b=6时,原式=4,与b的值无关.
例5.(1)水库中水位第一天连续下降了a小时,每小时平均下降2cm;第二天连续上升了a小时,每小时平均上升0.5cm,这两天水位总的变化情况如何?
解:把下降的水位变化量记为负,上升的水位变化量记为正,
第一天水位的变化量为-2a cm,第二天水位的变化量为0.5a cm.
两天水位的总变化量为:-2a+0.5a=(-2+0.5)a=-1.5a cm
四、典型例题
(四)合并同类项的应用
(2)某商店原有5袋大米,每袋大米为x千克,上午卖出3袋, 下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克
解:把进货的数量记为正,售出的数量记为负,进货后这个商店共
有大米5x-3x+4x=(5-3+4)x=6x千克.
四、典型例题
【当堂检测】
7.某中学3名老师带着18名学生去某景点写生,门票有两种购买方法:一种是老师每人a元,学生半价;一种是不论老师学生一律七五折,请你帮他们算一算,按哪种方法购买门票比较省钱.
解:第一种购票方法所需费用为3a+18×0.5a=12a(元)
第二种购票方法所需费用为(18+3)×0.75a=15.75a(元),
因为12a<15.75a,所以第一种购票方法较省钱.
第二章 整式的加减
2.2 整式的加减 第1课时
1.通过实例理解同类项的定义;
一、学习目标
2.知道只有同类项之间才能进行加减运算,掌握合并同类项的方法;
3.学会将一个多项式进行升(降)幂排列;即按一个字母的次数的
大小规律排列.
二、新课导入
观察下列物品摆放
饮料摆放
水果摆放
思考:这些物品摆放有什么特点?
三、概念剖析
根据下列单项式的特征将它们进行分组
8n,-7a2b,3ab2,2a2b,6,5n,-3,-ab2
(一)同类项的定义
分组1:
8n,5n
6,-3
-7a2b,3ab2
2a2b,-ab2
分组2:
8n,5n
6,-3
-7a2b,2a2b
3ab2,
-ab2
三、概念剖析
所含字母相同,并且相同字母的指数也分别相同的项叫做同类项
例如上面分组中单项式5n和8n是同类项,-7a2b和2a2b是同类项;-7a2b
和3ab2不是同类项,因为它们字母的指数不相同.
所有的常数项也看做同类项
(一)同类项的定义
例如上面分组中单项式6和-3是同类项.
三、概念剖析
定义:像8t-6t =(8-6)t=2t,4a2b+3a2b=(4+3)a2b=7a2b这样把多项式中的同类项合并成一项,叫做合并同类项
合并同类项法则:把同类项的系数相加的结果作为合并后的系数,字母和字母的次数不变
(二)合并同类项
4 a2b+ 3 a2b= 7 a2b
相加
不变
三、概念剖析
把一个多项式按照某个字母指数从大到小排列,叫降幂排列.
(三)多项式的排列
如:a2 + a-1
注意:交换项的位置时,要连同项的符号一起交换!
把一个多项式按照某个字母指数从小到大排列,叫升幂排列.
如:-1+a+a2
四、典型例题
(一)同类项的定义
例1.下列的每组式子分别是同类项吗?
(1)2x2与-x2 (2)3a2b与3ab2
(3)4m2n3与2n3m2 (4)3π2a与-2a
(5)6与-0.5 (6)8s与11t
是
不是
是
是
是
不是
如图,要表示左边这个图形的面积,有以下几种不同的方法:
右边两个图中的图形面积是否相等呢 显然是相等的,于是我们可以得到一个等式:(x+3)×3=3x+3×3.
可见,代数式去括号法则与有理数的去括号法则是一样的.
阅读教材本课时所有内容,回答下列问题.
1.(1)如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号 ;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号 .
(2)括号前只有因数“+”或者“-”号的,可以分别看作数字因数是 或者 .
相反
整式去括号法则
-1
1
相同
化简下列各式.
(1)(5a+3b)-(3a-2b)
=5a+3b
= ;
-3a+2b
2a+5b
(2)2(4x-6y)-3(2x+3y-1)
=8x-12y
= .
-6x-9y+3
2x-21y+3
·导学建议·
去括号是整式运算中的基础运算,重点强调学生按照相应的步骤进行计算,先去括号,然后进行合并同类项.尤其注意括号外面有系数以及负号时,更要认真计算,避免前面变了号,后面就忘了变号.
·学习小助手·
对于有多重括号的整式,特别是括号外面还有负号的式子,在去括号的时候注意从里到外层层“脱落”,并注意遇到括号外面是负号的,每个式子都得变号.
去括号法则
1.下列去括号,正确的是 ( )
A.a2-(2a-1)=a2-2a-1
B.a2+(2a-3)=a2-2a+3
C.-(a+b)+(c-d)=-a-b-c+d
D.-(a+b)+(d-1)=-a-b+d-1
D
添括号
2.将多项式3x3-2x2+4x-5添括号后正确的是 ( )
A.3x3-(2x2+4x-5)
B.(3x3+4x)-(2x2+5)
C.(3x3-5)+(-2x2-4x)
D.2x2+(3x3+4x-5)
B
方法归纳交流 添括号法则:①所添括号前面是“+”号,括到括号里的各项都不变符号;②所添括号前面是“-”号,括到括号里的各项都改变符号.
变式演练 不改变x-(y-3z)的值,把括号前的“-”号变成“+”号,结果应是( )
A.x+(y-3z) B.x+(-y-3z)
C.x+(y+3z) D.x+(-y+3z)
D
3.先去括号,再合并同类项.
(1)6a+(4a-2b); (2)x-3(2x+5y-6).
解:(1)原式=10a-2b;
(2)原式=-5x-15y+18.
去括号合并同类项
变式演练 先化简,再求值:
解:原式=3a-2a2-(5a-2a2+3a-4a2)=3a-2a2-5a+2a2-3a+4a2=4a2-5a.
4.为资助贫困地区儿童入学,某校甲、乙、丙三位同学决定把平时节省下来的零花钱捐给希望工程.已知甲同学捐款x元,乙同学的捐款数比甲同学的3倍少6元,丙同学的捐款数是甲的2倍.
(1)甲、乙、丙的捐款总数是多少元
(2)当x=30时,甲、乙、丙共捐款多少元
解:(1)由题知乙同学捐款(3x-6)元,丙同学捐款2x元.所以甲、乙、丙三人共捐款:x+(3x-6)+2x=6x-6(元).
(2)当x=30时,原式=6×30-6=180-6=174(元).
用去括号法则解决实际问题
·导学建议·
本节课初步学习了用整式去括号法则解决实际问题,下一个课时将进一步学习用整式的加减运算解决代数问题与实际问题.
·学习小助手·
去括号与添括号一样,关注括号外面的符号,如果是正号,里面的符号都不变.如果是负号,里面的符号都改变,要养成及时检查的习惯.
1.当a=-1,b=2时,代数式3a+b+2(3a+b)+1的值为 ( )
A.-2 B.0
C.1 D.3
A
2.化简-[-(-a2)-b2]-[+(-b2)]的结果是 ( )
A.2b2-a2 B.-a2
C.a2 D.a2-2b2
3.多项式mx2-(1-x-6x2)化简后不含x的二次项,则m的值为 .
-6
A
四、典型例题
例2.已知3x2my3 和 -2x2yn 是同类项,则式子m+n的值是多少?
(一)同类项的定义
解:因为3x2my3 和 -2x2yn 是同类项,所以2m=2,3=n ,所以
m=1,n=3;则m+n=4.
总结:两个式子是否为同类项与系数无关,与字母顺序无关;几个
常数项也是同类项.
四、典型例题
【当堂检测】
1.判断下列各组是否是同类项,是打“√”,不是打“×”.
(1) 3x与 3mx ( ) (2) 2ab与 -5ab ( )
(3) 5ab2与 -2ab2c ( ) (4) 23与 32 ( )
√
×
×
√
【当堂检测】
2.若5x3yn和﹣xmy2是同类项,则3m﹣7n= .
-5
四、典型例题
(二)合并同类项
例3.合并下列各式的同类项
(1)-2a2b+3ab2-3a2b+2ab2 (2)3x2+5xy+y2-3x2-3xy
解:(1)原式=(-2-3)a2b+(3+2)ab2=-5a2b+5ab2
(2)原式=(3-3)x2+(5-3)xy+y2=2xy+y2
总结:合并同类项时:先找出多项式中的同类项;再利用加法的交换
律,将不同类的同类项集中到不同的括号内;最后将同一括号
内的同类项相加即可.
四、典型例题
【当堂检测】
3.x2y -πx+x3y2+3按照x指数进行升幂排列为 .
3-πx+x2y+x3y2
总结:进行降幂排列,交换项的位置时,要连同项的符号一起交换.
【当堂检测】
4.合并同类项:
解:原式=(2+1-2)a+(1-2)b
=a-b
解:原式=(3-5+3)a +(1-7)ab+(-1+7)b
=a -6ab+6b
例4.(1)求多项式2x2 -5x+x2 +4x-3x2 -2的值,其中x=1.
解:2x2-5x+x2+4x-3x2-2=(2+1-3)x2+(-5+4)x-2=-x-2
当x=1时,原式=-1-2=-3.
四、典型例题
(三)化简、求值
(2)化简、求值: 其中 .
解:
四、典型例题
当 时,
原式
【当堂检测】
5.当x=-1时,求-x +2x+x -x+1的值.
解:-x2+2x+x2-x+1
=-x2+x2+2x-x+1
=(-x2+x2)+(2x-x)+1
=x+1.
当x=-1时,原式=-1+1=0.
【当堂检测】
6.有一道题,求3a2-4a2b+3ab+4a2b-ab+a2-2ab的值,其中a=-1,b=6,小明同学把b=6错写成了b=9,但他计算的结果是正确的,请你通过计算说明这是怎么回事.
解:原式=4a2,当a=-1,b=6时,原式=4,与b的值无关.
例5.(1)水库中水位第一天连续下降了a小时,每小时平均下降2cm;第二天连续上升了a小时,每小时平均上升0.5cm,这两天水位总的变化情况如何?
解:把下降的水位变化量记为负,上升的水位变化量记为正,
第一天水位的变化量为-2a cm,第二天水位的变化量为0.5a cm.
两天水位的总变化量为:-2a+0.5a=(-2+0.5)a=-1.5a cm
四、典型例题
(四)合并同类项的应用
(2)某商店原有5袋大米,每袋大米为x千克,上午卖出3袋, 下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克
解:把进货的数量记为正,售出的数量记为负,进货后这个商店共
有大米5x-3x+4x=(5-3+4)x=6x千克.
四、典型例题
【当堂检测】
7.某中学3名老师带着18名学生去某景点写生,门票有两种购买方法:一种是老师每人a元,学生半价;一种是不论老师学生一律七五折,请你帮他们算一算,按哪种方法购买门票比较省钱.
解:第一种购票方法所需费用为3a+18×0.5a=12a(元)
第二种购票方法所需费用为(18+3)×0.75a=15.75a(元),
因为12a<15.75a,所以第一种购票方法较省钱.
