期末真题分类特训:选择题-数学六年级上册苏教版(含解析)
文档属性
| 名称 | 期末真题分类特训:选择题-数学六年级上册苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末真题分类特训:选择题-数学六年级上册苏教版
1.(2022上·江苏镇江·六年级校考期末)把2个棱长1分米的正方体拼成一个长方体后,表面积比原来减少了( )。
A. B. C. D.
2.(2022上·江苏盐城·六年级统考期末)一个长2分米、宽6厘米、高5厘米的长方体盒子,最多能放( )个棱长是2厘米的正方体木块。
A.6 B.75 C.60 D.无法确定
3.(2022上·江苏扬州·六年级统考期末)图( )是下面正方体的展开图。
A. B.。 C. D.
4.(2022上·江苏淮安·六年级统考期末)一个长方体,如果高减少3厘米,就变成一个正方体。这时表面积比原来减少48平方厘米。原来长方体的体积是( )立方厘米。
A.48 B.64 C.96 D.112
5.(2022上·河南平顶山·六年级统考期末)硬纸包装的长方体酸奶盒,从外面量长5厘米、宽4厘米、高11厘米,它所装酸奶的量比较合理的应该是( )。
A.230毫升 B.200毫升 C.120毫升
6.(2022上·广西防城港·六年级统考期末)体积是30立方厘米的长方体木块,挖掉一块正方体后,表面积( )。
A.比原来小 B.比原来大 C.和原来同样大
7.(2022上·江苏泰州·六年级校考期末)把长7厘米,宽5厘米,厚3厘米的长方体肥皂两块包装在一起,用( )平方厘米包装纸最节省。
A.127 B.242 C.214 D.254
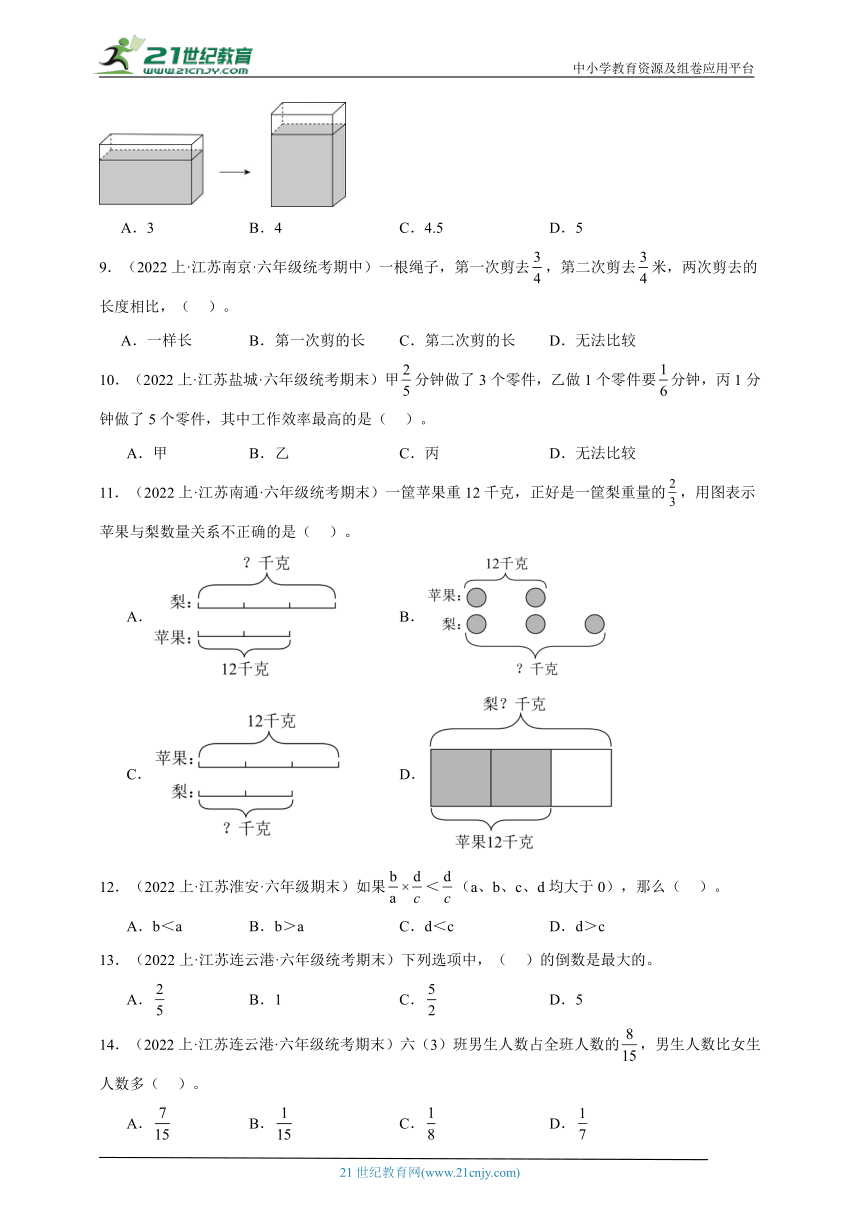
8.(2022上·江苏常州·六年级统考期末)一个密封玻璃缸,存水的空间长6分米、宽1分米、高4分米,现在缸内的水深3分米。如果把缸竖起来(如图),缸内水深( )分米。
A.3 B.4 C.4.5 D.5
9.(2022上·江苏南京·六年级统考期中)一根绳子,第一次剪去,第二次剪去米,两次剪去的长度相比,( )。
A.一样长 B.第一次剪的长 C.第二次剪的长 D.无法比较
10.(2022上·江苏盐城·六年级统考期末)甲分钟做了3个零件,乙做1个零件要分钟,丙1分钟做了5个零件,其中工作效率最高的是( )。
A.甲 B.乙 C.丙 D.无法比较
11.(2022上·江苏南通·六年级统考期末)一筐苹果重12千克,正好是一筐梨重量的,用图表示苹果与梨数量关系不正确的是( )。
A. B.
C. D.
12.(2022上·江苏淮安·六年级期末)如果×<(a、b、c、d均大于0),那么( )。
A.b<a B.b>a C.d<c D.d>c
13.(2022上·江苏连云港·六年级统考期末)下列选项中,( )的倒数是最大的。
A. B.1 C. D.5
14.(2022上·江苏连云港·六年级统考期末)六(3)班男生人数占全班人数的,男生人数比女生人数多( )。
A. B. C. D.
15.(2022上·福建宁德·六年级统考期末)若把甲仓存粮的运给乙仓,则两仓存粮量相等,那么原来( )。
A.甲仓比乙仓多存 B.乙仓占甲仓的
C.乙仓比甲仓少存 D.甲仓比乙少
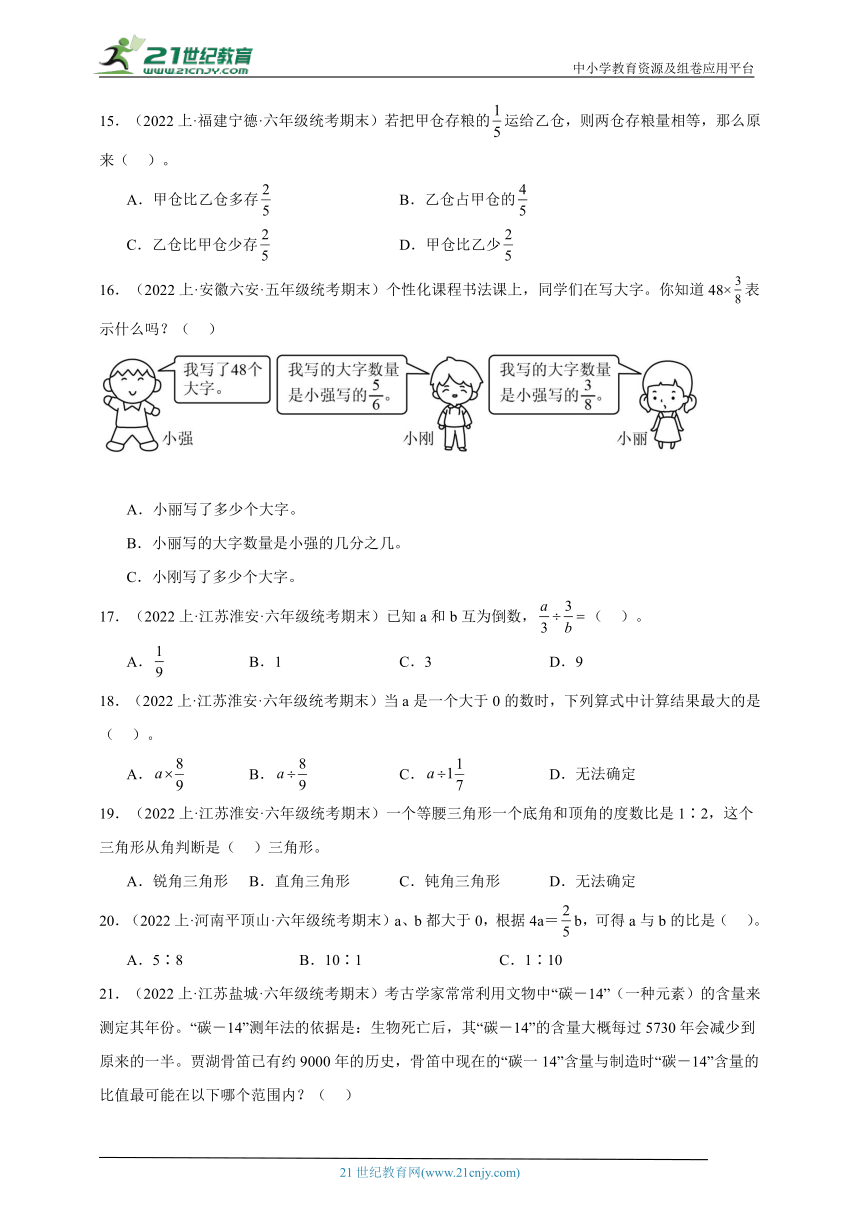
16.(2022上·安徽六安·五年级统考期末)个性化课程书法课上,同学们在写大字。你知道48×表示什么吗?( )
A.小丽写了多少个大字。
B.小丽写的大字数量是小强的几分之几。
C.小刚写了多少个大字。
17.(2022上·江苏淮安·六年级统考期末)已知a和b互为倒数,( )。
A. B.1 C.3 D.9
18.(2022上·江苏淮安·六年级统考期末)当a是一个大于0的数时,下列算式中计算结果最大的是( )。
A. B. C. D.无法确定
19.(2022上·江苏淮安·六年级统考期末)一个等腰三角形一个底角和顶角的度数比是1∶2,这个三角形从角判断是( )三角形。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
20.(2022上·河南平顶山·六年级统考期末)a、b都大于0,根据4a=b,可得a与b的比是( )。
A.5∶8 B.10∶1 C.1∶10
21.(2022上·江苏盐城·六年级统考期末)考古学家常常利用文物中“碳-14”(一种元素)的含量来测定其年份。“碳-14”测年法的依据是:生物死亡后,其“碳-14”的含量大概每过5730年会减少到原来的一半。贾湖骨笛已有约9000年的历史,骨笛中现在的“碳一14”含量与制造时“碳-14”含量的比值最可能在以下哪个范围内?( )
A. B. C. D.
22.(2022上·江苏常州·六年级统考期末)加工一个零件要小时,小时能加工多少个零件?下列解答正确的是( )。
A.÷=(个) B.÷=3(个)
C.×=(个) D.+=(个)
23.(2022上·江苏盐城·六年级统考期末)一套课桌椅的价格是320元,其中椅子的价格是课桌的,课桌的价格是( )元。
A.120 B.192 C.128 D.200
24.(2022上·江苏南通·六年级统考期末)把四根绳子分别放在盒子里,露出来的部分一样长,绳子最长的是( )。
A. B.
C. D.
25.(2022上·江苏南通·六年级统考期末)将的前项加上6,要使比值不变,后项应该( )。
A.加上6 B.乘2 C.加上8 D.乘3
26.(2019上·福建莆田·六年级统考期末)从甲地到乙地,货车用了4小时,客车用了6小时,货车和客车速度比是( )。
A.4∶6 B.2∶3 C.3∶2 D.6∶4
27.(2022上·江苏宿迁·六年级统考期末)甲数比乙数多3,甲数的4倍与乙数的4倍的和是332,甲数是( )。
A.40 B.43 C.32
28.(2022上·江苏徐州·六年级统考期末)根据左边的天平,想一想,要使右边的天平平衡,在方框里只放白球,要放( )个。
A.4 B.5 C.6 D.7
29.(2022上·山西临汾·六年级统考期末)4个水瓶和6个茶杯共220元。每个水瓶比每个茶杯贵30元。每个茶杯( )元。
A.10 B.28 C.30
30.(2022上·江苏苏州·六年级统考期末)8块高钙饼干的钙含量相当于1杯牛奶的钙含量,小欣早晨吃了12块高钙饼干,喝了1杯牛奶,合计含钙600毫克。一杯牛奶的钙含量是( )毫克。
A.240 B.20 C.360 D.30
31.(2022上·江苏·六年级校考期末)如图,3个杯子叠起来高15厘米,5个杯子叠起来高19厘米。个杯子叠起来的高度是( )厘米。
A. B. C. D.
32.(2021上·山西临汾·六年级统考期末)根据如图,=( )克。
A.50 B.48 C.64
33.(2022上·河南平顶山·六年级统考期末)有一道古题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”你得出的这道古代名题的结果是( )。
A.鸡14只,兔21只 B.鸡21只,兔14只
C.鸡23只,兔12只 D.鸡12只,兔23只
34.(2022上·江苏南通·六年级校考期末)如果用替换的策略解决下面的问题,可以选择哪个条件?
用30元买了2支钢笔和4支圆珠笔,( ),圆珠笔和钢笔的单价各是多少元?
A.一支圆珠笔比一支钢笔便宜3元B.买钢笔用去14元 C.买圆珠笔用去16元
35.(2022上·江苏常州·六年级统考期末)下列( )填在算式×+÷□的方框中,这个算式就能简便计算。
A.6 B. C. D.
36.(2022上·江苏徐州·六年级统考期末)一位同学把(a+)×3错当成a+×3进行计算,这样计算与正确的结果相差30。a的值是( )。
A.15 B.20 C.25 D.30
37.(2022上·江苏连云港·六年级统考期末)一桶油漆重18千克,用去,还剩( )千克。
A. B.3 C.15 D.
38.(2022上·江苏连云港·六年级统考期末)运算顺序是( )。
A.除、加、减 B.加、除、减 C.除、减、加 D.减、加、除
39.(2022上·安徽合肥·六年级统考期末)有甲、乙两根绳子,甲绳先用去米,再用去剩下的;乙绳先用去,再用去米,结果两根绳子剩下的长度相等,原来两根绳子相比,( )。
A.甲绳长 B.乙绳长 C.一样长
40.(2022上·山西临汾·六年级统考期末)光明小学有600名学生,其中女生占,后来转来一批男生,这时女生人数占总人数的,转来男生( )人。
A.120 B.80 C.240
41.(2019下·全国·六年级统考小升初模拟)水结成冰后体积会增加,那么冰化成水后体积会减少( )。
A. B. C. D.
42.(2022上·河南平顶山·六年级统考期末)刘叔叔去年使用微信消费1.8万元,__________。使用支付宝消费多少万元?如果用算式解决问题,横线上应补充下面信息( )。
A.使用微信消费比支付宝少 B.使用支付宝消费比微信少
C.使用支付宝消费是微信的 D.使用支付宝消费比微信多
43.(2022上·江苏淮安·六年级统考期末)在含盐率为20%的盐水中加入20克盐和20克水,盐水的浓度( )。
A.提高了 B.降低了 C.没有改变 D.无法确定
44.(2022上·江苏淮安·六年级统考期末)六(1)班星期一这天2人生病请假未到校,3人迟到,45人正常到校,六(1)班星期一这天的出勤率是( )%。
A.90% B.94% C.96% D.98%
45.(2022上·江苏宿迁·六年级统考期末)鲜蘑菇经晾干后减少原重量的85%,现有干蘑菇15千克,它是由多少千克鲜蘑菇晾干成的?列算式是( )。
A.15÷85% B.15×(1-85%) C.15÷(1-85%)
46.(2022上·江苏盐城·六年级统考期末)用4G下载一部《流浪地球》电影需要300秒,如果用5G下载所需时间约是4G的10%,只需( )秒。
A.50 B.30 C.0.03 D.15
47.(2022上·江苏宿迁·六年级统考期末)一杯糖水的含糖率是20%,加入6克糖和10克水后,这杯糖水的含糖率比原来( )。
A.提高了 B.降低了 C.不变
48.(2022上·江苏扬州·六年级统考期末)在含糖率8%的糖水中加入8克糖和100克水,现在糖水的含糖率( )。
A.变低了 B.变高了
C.不变 D.无法确定
49.(2022上·江苏盐城·六年级统考期末)一台电脑,将原标价先提价10%,再降价10%,结果两次调价后的价格比原来标价( )。
A.高 B.低 C.相等 D.无法比较
50.(2022上·江苏盐城·六年级统考期末)一杯糖水的含糖率是20%,喝去半杯后,含糖率是( )。
A.小于20% B.大于20% C.等于20% D.无法确定
参考答案:
1.C
【分析】减少的表面积就是重合的两个正方形的面积,用减少的表面积除以原来的表面积,即为表面积比原来减少了几分之几,据此解答。
【详解】1×1×2=2(平方分米)
2÷(1×1×6×2)
=2÷12
=
所以表面积比原来减少了。
故答案为:C
【点睛】解答本题的关键是明确减少的表面积也就是重合的两个正方形的面积。
2.C
【分析】求长方体盒子最多能放几个棱长是2厘米的正方体木块,就是求长方体的长、宽、高里分别有几个2厘米,用除法计算;再根据长方体的体积公式V=abh,把长、宽、高最多能放小正方体的个数相乘,即可求出小正方体的总个数。注意单位的换算:1分米=10厘米。
【详解】2分米=20厘米
20÷2=10(个)
6÷2=3(个)
5÷2=2(个)……1(厘米)
一共:10×3×2=60(个)
最多能放60个棱长是2厘米的正方体木块。
故答案为:C
【点睛】先分别求出长方体的长、宽、高最多能放几个小正方体,再利用长方体体积公式求出小正方体的总个数。
3.C
【分析】根据正方体的视图可知,带点的面和涂色面是相邻面,根据图形的折叠可知,选项A、D折成正方体后,带点的面和涂色面是相对面,B不是正方体的展开图,只有C折成正方体后,带点的面和涂色面是相邻面。据此判断即可。
【详解】根据正方体的视图可知,带点的面和涂色面是相邻面。
A.折成正方体后,带点的面和涂色面是相对面,不符合题意;
B.不是正方体的展开图,不符合题意;
C.折成正方体后,带点的面和涂色面是相邻面,符合题意;
D.折成正方体后,带点的面和涂色面是相对面,不符合题意。
故答案为:C
【点睛】此题考查了学生的空间想象能力以及对正方体展开图的熟练掌握程度。
4.D
【分析】根据长方体的高减少3厘米,就剩下一个正方体可知,这个正方体比原长方体表面积减少的高为3厘米的长方体的侧面积,即48平方厘米,则剩下的正方体的棱长为48÷4÷3=4厘米,原长方体的高为4+3=7厘米,再根据长方体的体积公式:V=abh,据此计算即可。
【详解】48÷4÷3
=12÷3
=4(厘米)
4+3=7(厘米)
4×4×7
=16×7
=112(立方厘米)
则原来长方体的体积是112立方厘米。
故答案为:D
【点睛】本题考查长方体的体积,求出原来长方体的长、宽和高是解题的关键。
5.B
【分析】根据体积、容积的意义,物体所占空间的大小叫做物体的体积,物体所容纳物体的体积叫做物体的容积。一个容器壁再薄也有厚度,因此,一个物体的容积要小于它的体积。根据长方体的体积=长×宽×高,用5×4×11即可求出长方体盒装的体积,它的容积比它的体积要小,据此解答。
【详解】5×4×11=220(立方厘米)
220立方厘米=220毫升
A.230毫升>220毫升
不符合题意;
B.200毫升<220毫升
符合题意;
C.120毫升<220毫升
120毫升太少,不符题意。
它所装酸奶的量比较合理的应该是200毫升。
故答案为:B
【点睛】本题主要是考查物体体积、容积的意义以及长方体体积公式的应用。物体体积、容积计算方法虽然相同。但度量时不同,计算体积从外面度量,计算容积从里面度量。
6.C
【分析】根据图意可知,从一个顶点处沿着长宽高挖掉一个小正方体,减少的面与增加的面个数是相等的都是3个面,所以长方体的表面积没发生变化。
【详解】因为在长方体的顶点上挖掉一个小正方体后,对于这个图形减少的面与增加的面个数是相等的都是3个,所以长方体的表面积没发生变化。
故答案为:C
【点睛】本题考查了关于长方体的表面积的问题,考查了学生观察,分析,解决问题的能力。
7.C
【分析】把这两块肥皂包装在一起,要想使表面积最小,那么应该把它们的最大的面相粘合,由此拼成的新长方体的长、宽、高分别是:7厘米、5厘米、6厘米,根据长方体的表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】把这两块肥皂包装在一起,拼成的新长方体的长、宽、高分别是:7厘米、5厘米、3×2=6(厘米)
(7×5+7×6+5×6)×2
=(35+42+30)×2
=(77+30)×2
=107×2
=214(平方厘米)
把长7厘米,宽5厘米,厚3厘米的长方体肥皂两块包装在一起,用214平方厘米包装纸最节省。
故答案为:C
【点睛】此题主要考查长方体的表面积公式的灵活运用;解答关键是理解:把它们的最大的面相粘合,包装最省纸。
8.C
【分析】根据题意可知:玻璃缸无论横放还是竖放水的体积不变,首先根据长方体的体积公式:体积=长×宽×高;求出玻璃缸内水的体积,然后用水的体积除以竖放时玻璃缸的底面积即可。
【详解】6×1×3÷(1×4)
=6×3÷4
=18÷4
=4.5(分米)
如果把缸竖起来,缸内水深4.5分米。
故答案为:C
【点睛】熟练掌握和灵活运用长方体体积公式是解答本题的关键。
9.B
【分析】把这根绳子的长度当作单位“1”,第一次剪去全长的,则剩下的占全长的(1-),即,因为 >,所以第二次不管剪去多少,都比第一次剪去的少。
【详解】1-=
>,第一次剪的长。
一根绳子,第一次剪去,第二次剪去米,两次剪去的长度相比,第一次长。
故答案为:B
【点睛】解答本题的关键是区分两个,一个是分率,一个是具体数量。
10.A
【分析】根据工作效率=工作量÷工作时间这一公式,分别算出甲、乙、丙三人的工作效率,再比较即可。
【详解】甲:3÷
=
=
乙:1÷
=1×6
=6
丙:5÷1=5
因为>6>5,所以丙的效率最甲。
故答案为:A
【点睛】此题考查了分数除法运算以及工作量、工作时间、工作效率三者之间的关系。
11.C
【分析】由题意可知,把梨的重量看作单位“1”,平均分成3份,其中的2份就是苹果的重量,即12千克,据此逐一分析各项即可。
【详解】A.表示把梨的重量看作单位“1”,平均分成3份,其中的2份就是苹果的重量,符合题意;
B.表示把梨的重量看作单位“1”,平均分成3份,其中的2份就是苹果的重量,符合题意;
C.表示把苹果的重量看作单位“1”,平均分成3份,其中的2份就是梨的重量,不符合题意;
D.表示把梨的重量看作单位“1”,平均分成3份,其中的2份就是苹果的重量,符合题意。
故答案为:C
【点睛】本题考查求一个数的几分之几是多少,明确单位“1”是解题的关键。
12.A
【分析】一个数(0除外)乘小于1的数,积比原来的数小。
分子比分母小的分数叫做真分数;真分数<1。
【详解】×<
则<1,那么b<a。
故答案为:A
【点睛】本题考查判断积与因数之间大小关系的方法以及真分数的认识。
13.A
【分析】根据倒数的意义,乘积是1的两个数互为倒数。求真分数和假分数的倒数时,把分子和分母调换位置即可,最后比较大小。
【详解】的倒数是;1的倒数是1;的倒数是;5的倒数是;
>1>>
的倒数是最大的。
故答案为:A
【点睛】此题考查的目的是理解倒数的意义,掌握求倒数的方法。
14.D
【分析】假设全班人数为30人,已知男生人数占全班人数的,则把全班人数看作单位“1”,根据分数乘法的意义,用30×即可求出男生人数,然后用全班人数减去男生人数,即可求出女生人数;求一个数比另一个数多几分之几,用相差数除以另一个数,则用男女生人数差除以女生人数,即可求出男生人数比女生人数多几分之几。
【详解】假设全班人数为30人,
男生:30×=16(人)
女生:30-16=14(人)
(16-14)÷14
=2÷14
=
男生人数比女生人数多。
故答案为:D
【点睛】本题主要考查了分数的应用,可用假设法解决问题,明确求一个数比另一个数多几分之几,用除法计算。
15.C
【分析】把甲仓库的吨数看作单位“1”,平均分成5份,每份是它的,把其中1份运给乙仓库,则两仓库存粮相等,说明甲仓库比乙仓库多这样的2份,乙仓库比甲仓库少2个,即,据此解答。
【详解】×2=
若把甲仓存粮的运给乙仓,则两仓存粮量相等,那么原来乙仓比甲仓少存。
故答案为:C
【点睛】本题考查分数的意义,关键明确:把甲仓库原来存粮的吨数平均分成5份,比乙仓库多2份,这两份就是。
16.A
【分析】把小强写的大字的个数看作单位“1”,是小丽写的大字占小强写的大字的分率,所以48×表示小丽写了多少个大字;据此选择即可。
【详解】8×表示小丽写了多少个大字。
故答案为:A。
【点睛】本题主要考查了分数乘法应用题,解题的关键是掌握:求一个数的几分之几是多少,用乘法计算。
17.A
【分析】根据倒数的意义可知,a×b=1,把a×b=1代入,计算即可。
【详解】
=
=
=
故答案为:A
【点睛】此题考查了用字母表示数、倒数的意义以及分数除法。
18.B
【分析】一个不为零的数乘上一个小于1的数,结果比原数小;一个不为零的数乘上一个大于1的数,结果比原数大。
【详解】A.因为,所以<a
B.=,因为,所以>a;
C.,因为,所以<a;
D.说法错误。
故答案为:B
【点睛】此题考查了积与乘数之间的关系。要求熟练掌握并灵活运用。
19.B
【分析】根据等腰三角形的两个底角相等,则等腰三角形的三个内角的度数比为1∶1∶2,再根据三角形的内角和是180°,根据按比例分配的方法,求出最大角的度数,再根据三角形按照角的大小分类情况进行判断即可。
【详解】180°÷(1+1+2)
=180°÷4
=45°
45°×2=90°
则有一个角是90度的三角形是直角三角形,所以这个三角形是直角三角形。
故答案为:B
【点睛】本题考查按比分配问题,结合等腰三角形的特征是解题的关键。
20.C
【分析】可以设4a=b=1,然后根据“因数=积÷另一个因数”,分别求出a、b的值,再根据比的意义写出a与b的比,最后化简比即可。
【详解】设4a=b=1。
a=1÷4=
b=1÷=1×=
a∶b
=∶
=(×4)∶(×4)
=1∶10
a与b的比是1∶10。
故答案为:C
【点睛】本题考查比的意义以及化简比,运用赋值法,根据乘法中各部分的关系计算出a、b的值是解题的关键。
21.B
【分析】根据题意,可以假设原来的含量为单位“1”,则5730年后为,9000大约是5720的1.5倍,不超过2倍。所以9000年后含有的量比÷2=×=多,比少。
【详解】设原来的含量为1,则5730年后为,所以9000年后含有的量比值在之间。
故答案为:B
【点睛】此题考查了分数的意义,要求熟练掌握并灵活运用。
22.B
【分析】已知加工一个零件要小时,求小时能加工多少个零件,就是求里面有几个,用除法计算。
【详解】÷
=×6
=3(个)
小时能加工3个零件。
解答正确的是:÷=3(个)
故答案为:B
【点睛】本题考查分数除法的应用,理解包含除法的意义是解题的关键。
23.D
【分析】将课桌价格看作单位“1”,一套课桌椅的价格是课桌价格的(1+),一套课桌椅的价格÷对应分率=课桌的价格,据此列式计算。
【详解】320÷(1+)
=320÷
=320×
=200(元)
课桌的价格是200元。
故答案为:D
【点睛】关键是确定单位“1”,理解分数除法的意义。
24.A
【分析】露出来的部分一样长,可设露出的长度为1,根据分数除法的意义分别求出四根绳子的长度再比较即可。
【详解】设露出的长度为1
A.1÷=1×6=6,A选项这根长为6;
B.1÷=1×5=5,B选项这根长为5;
C.1÷=1×4=4,C选项这根长为4;
D.1÷=1×3=3,D选项这根长为3;
6>5>4>3,所以A选项这根绳子最长。
故答案为:A
【点睛】本题主要考查分数除法的应用,明确已知量÷对应分率=表示单位“1”的量是解题的关键。
25.D
【分析】根据比的基本性质:比的前项和后项同时乘或除以一个不为0的数,比值不变;用3+6,再除以3,求出比的前项扩大到原来的多少倍,进而求出后项扩大到原来的多少倍,即可解答。
【详解】(3+6)÷3
=9÷3
=3
将3∶8的前项加上6,要使比值不变,后项应该乘3。
故答案为:D
【点睛】熟练掌握比的基本性质是解答本题的关键。
26.C
【分析】把甲地到乙地的路程看作单位“1”,先分别求出货车和客车的速度,进而写出货车和客车的速度比并化简比。
【详解】货车的速度:1÷4=
客车的速度:1÷6=
货车和客车速度比:∶
=(×12)∶(×12)
=3∶2
货车和客车速度比是3∶2
故答案为:C
【点睛】此题关键是先求出货车和客车的速度,进而写出货车和客车的速度比并化简比。
27.B
【分析】甲数的4倍与乙数的4倍的和是332,则甲数与乙数的和是332÷4=83。根据甲数比乙数多3,可设甲数是x,则乙数是x-3。再根据等量关系“甲数+乙数=83”列出方程,解方程可求出甲数。
【详解】解:设甲数是x。
x+(x-3)=332÷4
x+x-3=83
2x-3=83
2x=83+3
2x=86
x=86÷2
x=43
所以甲数是43。
故答案为:B
【点睛】已知两个数的和与差,可以用字母表示数,列方程解答。
28.B
【分析】观察左边图形可知,左上角托盘两个大黑球和一个小白球等于右上角托盘一个大黑球和四个小白球,托盘两边同时减去一个大黑球和一个小白球,结果是左上角托盘一个大黑球等于右上角托盘三个小白球,观察右边图形可知,左上角托盘里有两个小白球和一个大黑球,一个大黑球等于三个小白球,由此可知,右上角托盘应该放2+3=5个白球,据此解答。
【详解】根据分析可知,根据左边的天平,想一想,要使右边的天平平衡,在方框里只放白球,要放5个小白球。
故答案为:B
【点睛】解答本题的关键是找出大黑球与小白球之间的关系。
29.A
【分析】根据题意可知,每个茶杯的价格+30元=每个水瓶的价格,根据单价×数量=总价,用水瓶的单价×水瓶的数量+茶杯的单价×茶杯的数量=220元,据此设每个茶杯x元,列方程为:(x+30)×4+6x=220,然后解出方程即可。
【详解】解:设每个茶杯x元。
(x+30)×4+6x=220
4x+120+6x=220
10x+120=220
10x+120-120=220-120
10x=100
10x÷10=100÷10
x=10
每个茶杯10元。
故答案为:A
【点睛】本题可用列方程解决问题,找到相应的关系式是解答本题的关键。
30.A
【分析】根据题意可知,8块高钙饼干的钙含量=1杯牛奶的钙含量,12块高钙饼干的钙含量+1杯牛奶的钙含量=含钙600毫克,则(12+8)块高钙饼干的钙含量=含钙600毫克,用600÷(12+8)即可求出1块高钙饼干的钙含量,再乘8即可求出1杯牛奶的钙含量。
【详解】600÷(12+8)×8
=600÷20×8
=240(毫克)
一杯牛奶的钙含量是240毫克。
故答案为:A
【点睛】根据对应的等量代换找到合适的解题方法即可。
31.B
【分析】根据图形可知,3个杯子叠在一起的总高度是一个杯子的高度与2个杯口上升高度的和,5个杯子叠在一起的总高度是一个杯子的高度与4个杯口上升高度的和;用19减去15即为两个杯口上升的高度,用除法计算,即可求出一个杯口上升的高度,进而求出一个杯子的高度;根据总高度=一个杯口上升的高度×(杯子个数-1)+一个杯子的高度,用字母表示即可解答。
【详解】(19-15)÷(5-3)
=4÷2
=2(厘米)
15-2×2
=15-4
=11(厘米)
2×(a-1)+11
=2a-2+11
=9+2a(厘米)
如图,3个杯子叠起来高15厘米,5个杯子叠起来高19厘米。a个杯子叠起来的高度是9+2a厘米。
故答案为:B
【点睛】解答本题的关键是先计算出一个叠加部分的高度和最下面一个杯子的高度,最后计算出n个杯子叠加起来的高度。
32.C
【分析】先由图1可以得到一个较大圆=24克,再由图2可知,一个小圆为24×2÷3=16(克),由图3可知,最大圆为16×4=64(克),据此解答即可。
【详解】图1可以得到一个较大圆是24克
由图2可知,一个小圆是
24×2÷3
=48÷3
=16(克)
由图3可知,最大圆是
16×4=64(克)
故答案为:C
【点睛】由图1可以得到一个较大圆=24克,再求出小圆的值,是解答此题的关键。
33.C
【分析】假设都是兔,则应有35×4=140足,比实际多140-94=46足,多出的足数是将每只鸡的足数多算4-2=2足,故鸡有46÷2=23只,兔有35-23=12只;据此解答。
【详解】鸡:(35×4-94)÷(4-2)
=(140-94)÷2
=46÷2
=23(只)
兔:35-23=12(只)
故答案为:C
【点睛】本题主要考查鸡兔同笼问题,解答此类问题通常采用假设法。
34.A
【分析】由于要用替换的策略解决问题,想要求圆珠笔和钢笔的单价各是多少,已经有了钢笔和圆珠笔各自支数的总价,此时需要知道钢笔和圆珠笔的单价之间的关系,这样才可以用替换法解决,据此即可选择。
【详解】由分析可知:
一支圆珠笔比一支钢笔便宜3元,这是钢笔和圆珠笔之间的关系,其它条件不符合。
故答案为:A
【点睛】本题主要考查简单的等量代还的计算及应用,理解题意,找出数量关系。
35.C
【分析】在分数计算中,除以一个不为0的数等于乘它的倒数,这个算式可以运用乘法分配律a×c+b×c=(a+b)×c,因为+=1,方框中可以填的倒数即。
【详解】×+×=×+÷
填在算式×+÷□的方框中,这个算式就能简便计算。
故答案为:C
【点睛】本题主要考查了分数的简便运算,明确整数的运算律在分数中同样适用。
36.A
【分析】因为(a+)×3比a+×3多30,则可列方程为(a+)×3-(a+×3)=30,然后根据等式的性质解方程即可。
【详解】(a+)×3-(a+×3)=30
解:3a+×3-a-×3=30
2a=30
a=30÷2
a=15
a的值是15。
故答案为:A
【点睛】根据题意列出方程并熟练掌握分数乘法的运算定律是解答题目的关键。
37.B
【分析】把一桶油漆的重量看作单位“1”,已知用去,则剩下的重量占总重量的(1-),根据分数乘法的意义,用18×(1-)即可求出还剩多少千克。
【详解】18×(1-)
=18×
=3(千克)
还剩3千克。
故答案为:B
【点睛】本题主要考查了分数乘法的应用,明确求一个数的几分之几是多少,用乘法计算。
38.D
【分析】如果一个算式中只有加减法或者只有乘除法,要从左到右按顺序计算;如果算式中既有加减法,又有乘除法,要先算乘除法,后算加减法;如果算式中有括号,要先算括号里的;如果既有中括号又有小括号,要先算小括号里的,再算中括号里面的,据此解答。
【详解】根据运算顺序,在计算÷[+(1-)]时,先计算小括号里的减法,再计算中括号里的加法,最后计算括号外的除法,所以运算顺序是减→加→除。
故答案为:D
【点睛】熟练掌握分数四则混合运算顺序和运算法则是解答本题的关键。
39.B
【分析】可设甲绳长x米,乙绳长y米,甲绳先用去米,再用去剩下的;乙绳先用去,再用去米,可知甲剩下(x-)×(1-)米,乙剩下y×(1-)-米,因为两根绳子剩下的长度相等,即(x-)×(1-)=y×(1-)-,可通过计算,得出x与y之间的关系,进而解答。
【详解】解:设甲绳长x米,乙绳长y米,根据题意可得:
(x-)×(1-)=y×(1-)-
(x-)×=y-
x-=y-
y-x=-
y-x=-
y-x=
9y-90x=1
90(y-x)=1
y-x=1÷90
y-x=
y>x,即乙绳长>甲绳长。
有甲、乙两根绳子,甲绳先用去米,再用去剩下的;乙绳先用去,再用去米,结果两根绳子剩下的长度相等,原来两根绳子相比,乙绳长。
故答案为:B
【点睛】理解数量米和分数的不同,找出甲、乙两根绳子剩下部分的等量关系是解答本题的关键。
40.C
【分析】由题意可知:女生人数不变,先将原来的学生人数看成单位“1”,根据分数乘法的意义,用600×求出女生人数;再将现在的人数看成单位“1”,根据分数除法的意义,用女生人数÷现在的分率,求出现在的人数,最后用现在人数-原来人数求出转来男生的人数。
【详解】600×÷-600
=350÷-600
=350×-600
=840-600
=240(人)
转来男生240人。
故答案为:C
【点睛】本题考查“求一个数的几分之几”及“已知一个数的几分之几是多少求这个数”的简单运用。
41.D
【分析】设水的体积是1;把水的体积看作单位“1”,则冰的体积是水的体积的(1+),再用水的体积×(1+),求出冰的体积,再用冰与水的体积差,除以冰的体积,即可求出冰化成水后体积会减少的分率;据此解答。
【详解】设水的体积是1。
1×(1+)
=1×
=
(-1)÷
=×
=
水结成冰后体积会增加,那么冰化成水后体积会减少。
故答案为:D
【点睛】解决此题关键是找准单位“1”,水结成冰,水的体积是单位“1”;冰化成水,冰的体积是单位“1”。
42.A
【分析】求一个数的几分之几是多少用乘法;已知一个数的几分之几是多少,求这个数用除法;据此逐项分析各选项即可。
【详解】A.使用微信消费比支付宝少,是将使用支付宝消费的钱数看成单位“1”,使用微信消费比支付宝少,则使用微信消费是支付宝的1-,求使用支付宝消费的钱数,用1.8÷(1-)计算,该选项符合题意;
B.使用支付宝消费比微信少,是将使用微信消费的钱数看成单位“1”,使用支付宝消费比微信少,则使用支付宝消费是微信的1-,求使用支付宝消费的钱数,用1.8×(1-)计算,该选项不符合题意;
C.使用支付宝消费是微信的,是将微信消费钱数看成单位“1”,求使用支付宝消费钱数,用1.8×计算,该选项不符合题意;
D.使用支付宝消费比微信多,是将微信消费钱数看成单位“1”,使用支付宝消费的钱数是微信的1+,求使用支付宝消费的钱数,用1.8×(1+)计算,该选项不符合题意;
故答案为:A
【点睛】熟练掌握求比一个数多\少几分之几的数是多少及已知比一个数多/少几分之几的数是多少,求这个数的解题方法是解题的关键。
43.A
【分析】根据含盐率=盐的重量÷盐水的重量×100%,已知盐重20克,水重20克,则盐水重20+20=40克,可求出加入盐水的含盐率,再同原来盐水的含盐率进行比较,若加入盐水的含盐率高于原来的含盐率,盐水的浓度就提高了,反之就降低了。
【详解】20÷(20+20)×100%
=20÷40×100%
=0.5×100%
=50%
50%>20%
则在含盐率为20%的盐水中加入20克盐和20克水,盐水的浓度提高了。
故答案为:A
【点睛】本题考查含盐率,明确含盐率的计算方法是解题的关键。
44.C
【分析】根据题意,先用正常到校的人数加上请病假的人数,再加上迟到的人数,求出六(1)班的总人数;用正常到校人数加上迟到人数,求出六(1)班今天出勤的人数。
再根据“出勤率=出勤的人数÷总人数×100%”,代入数据计算,即可求解。
【详解】(45+3)÷(45+2+3)×100%
=48÷50×100%
=0.96×100%
=96%
六(1)班星期一这天的出勤率是96%。
故答案为:C
【点睛】本题考查百分率问题,掌握出勤率的意义及计算方法是解题的关键。
45.C
【分析】根据题意,干蘑菇的质量比鲜蘑菇的质量少85%,那么干蘑菇的质量是鲜蘑菇质量的(1-85%)。将鲜蘑菇的质量看作单位“1”,单位“1”未知,用干蘑菇质量除以(1-85%),即可求出它是由多少千克鲜蘑菇晾干成的。
【详解】求15千克干蘑菇是由多少千克鲜蘑菇晾干成的?列算式是15÷(1-85%)。
故答案为:C
【点睛】本题考查了含百分数的运算,已知比一个数少百分之几的数是多少,求这个数用除法。
46.B
【分析】根据题意,可以用300乘上10%即可算出答案。
【详解】300×10%=30(秒),只需30秒。
故答案为:B
【点睛】此题考查了百分数的应用,要求熟练掌握并灵活运用。
47.A
【分析】用6克糖除以(6+10)克糖水,求出加入部分糖水的含糖率。如果它比原来的含糖率高,则最终整杯糖水的含糖率比原来就提高了。反之则降低,据此解题。
【详解】6÷(6+10)
=6÷16
=37.5%
37.5%>20%,所以加入6克糖和10克水后,这杯糖水的含糖率比原来提高了。
故答案为:A
【点睛】本题考查了百分率问题,求一个数是另一个数的百分之几,用这个数除以另一个数。
48.A
【分析】含糖率表示糖的质量占糖水质量的百分之几,计算方法:含糖率=糖的质量÷糖水的质量×100%,由此求出加入的糖水的含糖率,与原来的含糖率相比较,得出结论。
【详解】加入的糖水的含糖率:
8÷(8+100)×100%
=8÷108×100%
≈0.074×100%
=7.4%
7.4<8%
现在糖水的含糖率变低了。
故答案为:A
【点睛】本题考查百分率问题,掌握含糖率的意义及计算方法是解题的关键。
49.B
【分析】设这台电脑的原价是1,先提价10%,是把原价看作单位“1”,则提价后的价格是原价的(1+10%),单位“1”已知,根据百分数乘法的意义求出提价后的价格;
再降价10%,是把提价后的价格看作单位“1”,则降价后的价格是提价后价格的(1-10%);单位“1”已知,用乘法求出现价,再与原价相比较,得出结论。
【详解】设这台电脑的原价是1。
1×(1+10%)×(1-10%)
=1×1.1×0.9
=0.99
0.99<1
结果两次调价后的价格比原来标价低。
故答案为:B
【点睛】本题考查百分数乘法的应用,区分两个单位“1”的不同,明确求比一个数多或少百分之几的数是多少,用乘法计算。
50.C
【分析】含糖20%的糖水,喝去半杯后,剩下的糖水并没有加水,也没有加糖,因此含糖率不变,还是20%,据此分析。
【详解】根据分析,一杯糖水的含糖率是20%,喝去半杯后,含糖率不变,还是等于20%。
故答案为:C
【点睛】关键是理解百分率的意义,掌握百分率的求法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题分类特训:选择题-数学六年级上册苏教版
1.(2022上·江苏镇江·六年级校考期末)把2个棱长1分米的正方体拼成一个长方体后,表面积比原来减少了( )。
A. B. C. D.
2.(2022上·江苏盐城·六年级统考期末)一个长2分米、宽6厘米、高5厘米的长方体盒子,最多能放( )个棱长是2厘米的正方体木块。
A.6 B.75 C.60 D.无法确定
3.(2022上·江苏扬州·六年级统考期末)图( )是下面正方体的展开图。
A. B.。 C. D.
4.(2022上·江苏淮安·六年级统考期末)一个长方体,如果高减少3厘米,就变成一个正方体。这时表面积比原来减少48平方厘米。原来长方体的体积是( )立方厘米。
A.48 B.64 C.96 D.112
5.(2022上·河南平顶山·六年级统考期末)硬纸包装的长方体酸奶盒,从外面量长5厘米、宽4厘米、高11厘米,它所装酸奶的量比较合理的应该是( )。
A.230毫升 B.200毫升 C.120毫升
6.(2022上·广西防城港·六年级统考期末)体积是30立方厘米的长方体木块,挖掉一块正方体后,表面积( )。
A.比原来小 B.比原来大 C.和原来同样大
7.(2022上·江苏泰州·六年级校考期末)把长7厘米,宽5厘米,厚3厘米的长方体肥皂两块包装在一起,用( )平方厘米包装纸最节省。
A.127 B.242 C.214 D.254
8.(2022上·江苏常州·六年级统考期末)一个密封玻璃缸,存水的空间长6分米、宽1分米、高4分米,现在缸内的水深3分米。如果把缸竖起来(如图),缸内水深( )分米。
A.3 B.4 C.4.5 D.5
9.(2022上·江苏南京·六年级统考期中)一根绳子,第一次剪去,第二次剪去米,两次剪去的长度相比,( )。
A.一样长 B.第一次剪的长 C.第二次剪的长 D.无法比较
10.(2022上·江苏盐城·六年级统考期末)甲分钟做了3个零件,乙做1个零件要分钟,丙1分钟做了5个零件,其中工作效率最高的是( )。
A.甲 B.乙 C.丙 D.无法比较
11.(2022上·江苏南通·六年级统考期末)一筐苹果重12千克,正好是一筐梨重量的,用图表示苹果与梨数量关系不正确的是( )。
A. B.
C. D.
12.(2022上·江苏淮安·六年级期末)如果×<(a、b、c、d均大于0),那么( )。
A.b<a B.b>a C.d<c D.d>c
13.(2022上·江苏连云港·六年级统考期末)下列选项中,( )的倒数是最大的。
A. B.1 C. D.5
14.(2022上·江苏连云港·六年级统考期末)六(3)班男生人数占全班人数的,男生人数比女生人数多( )。
A. B. C. D.
15.(2022上·福建宁德·六年级统考期末)若把甲仓存粮的运给乙仓,则两仓存粮量相等,那么原来( )。
A.甲仓比乙仓多存 B.乙仓占甲仓的
C.乙仓比甲仓少存 D.甲仓比乙少
16.(2022上·安徽六安·五年级统考期末)个性化课程书法课上,同学们在写大字。你知道48×表示什么吗?( )
A.小丽写了多少个大字。
B.小丽写的大字数量是小强的几分之几。
C.小刚写了多少个大字。
17.(2022上·江苏淮安·六年级统考期末)已知a和b互为倒数,( )。
A. B.1 C.3 D.9
18.(2022上·江苏淮安·六年级统考期末)当a是一个大于0的数时,下列算式中计算结果最大的是( )。
A. B. C. D.无法确定
19.(2022上·江苏淮安·六年级统考期末)一个等腰三角形一个底角和顶角的度数比是1∶2,这个三角形从角判断是( )三角形。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
20.(2022上·河南平顶山·六年级统考期末)a、b都大于0,根据4a=b,可得a与b的比是( )。
A.5∶8 B.10∶1 C.1∶10
21.(2022上·江苏盐城·六年级统考期末)考古学家常常利用文物中“碳-14”(一种元素)的含量来测定其年份。“碳-14”测年法的依据是:生物死亡后,其“碳-14”的含量大概每过5730年会减少到原来的一半。贾湖骨笛已有约9000年的历史,骨笛中现在的“碳一14”含量与制造时“碳-14”含量的比值最可能在以下哪个范围内?( )
A. B. C. D.
22.(2022上·江苏常州·六年级统考期末)加工一个零件要小时,小时能加工多少个零件?下列解答正确的是( )。
A.÷=(个) B.÷=3(个)
C.×=(个) D.+=(个)
23.(2022上·江苏盐城·六年级统考期末)一套课桌椅的价格是320元,其中椅子的价格是课桌的,课桌的价格是( )元。
A.120 B.192 C.128 D.200
24.(2022上·江苏南通·六年级统考期末)把四根绳子分别放在盒子里,露出来的部分一样长,绳子最长的是( )。
A. B.
C. D.
25.(2022上·江苏南通·六年级统考期末)将的前项加上6,要使比值不变,后项应该( )。
A.加上6 B.乘2 C.加上8 D.乘3
26.(2019上·福建莆田·六年级统考期末)从甲地到乙地,货车用了4小时,客车用了6小时,货车和客车速度比是( )。
A.4∶6 B.2∶3 C.3∶2 D.6∶4
27.(2022上·江苏宿迁·六年级统考期末)甲数比乙数多3,甲数的4倍与乙数的4倍的和是332,甲数是( )。
A.40 B.43 C.32
28.(2022上·江苏徐州·六年级统考期末)根据左边的天平,想一想,要使右边的天平平衡,在方框里只放白球,要放( )个。
A.4 B.5 C.6 D.7
29.(2022上·山西临汾·六年级统考期末)4个水瓶和6个茶杯共220元。每个水瓶比每个茶杯贵30元。每个茶杯( )元。
A.10 B.28 C.30
30.(2022上·江苏苏州·六年级统考期末)8块高钙饼干的钙含量相当于1杯牛奶的钙含量,小欣早晨吃了12块高钙饼干,喝了1杯牛奶,合计含钙600毫克。一杯牛奶的钙含量是( )毫克。
A.240 B.20 C.360 D.30
31.(2022上·江苏·六年级校考期末)如图,3个杯子叠起来高15厘米,5个杯子叠起来高19厘米。个杯子叠起来的高度是( )厘米。
A. B. C. D.
32.(2021上·山西临汾·六年级统考期末)根据如图,=( )克。
A.50 B.48 C.64
33.(2022上·河南平顶山·六年级统考期末)有一道古题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”你得出的这道古代名题的结果是( )。
A.鸡14只,兔21只 B.鸡21只,兔14只
C.鸡23只,兔12只 D.鸡12只,兔23只
34.(2022上·江苏南通·六年级校考期末)如果用替换的策略解决下面的问题,可以选择哪个条件?
用30元买了2支钢笔和4支圆珠笔,( ),圆珠笔和钢笔的单价各是多少元?
A.一支圆珠笔比一支钢笔便宜3元B.买钢笔用去14元 C.买圆珠笔用去16元
35.(2022上·江苏常州·六年级统考期末)下列( )填在算式×+÷□的方框中,这个算式就能简便计算。
A.6 B. C. D.
36.(2022上·江苏徐州·六年级统考期末)一位同学把(a+)×3错当成a+×3进行计算,这样计算与正确的结果相差30。a的值是( )。
A.15 B.20 C.25 D.30
37.(2022上·江苏连云港·六年级统考期末)一桶油漆重18千克,用去,还剩( )千克。
A. B.3 C.15 D.
38.(2022上·江苏连云港·六年级统考期末)运算顺序是( )。
A.除、加、减 B.加、除、减 C.除、减、加 D.减、加、除
39.(2022上·安徽合肥·六年级统考期末)有甲、乙两根绳子,甲绳先用去米,再用去剩下的;乙绳先用去,再用去米,结果两根绳子剩下的长度相等,原来两根绳子相比,( )。
A.甲绳长 B.乙绳长 C.一样长
40.(2022上·山西临汾·六年级统考期末)光明小学有600名学生,其中女生占,后来转来一批男生,这时女生人数占总人数的,转来男生( )人。
A.120 B.80 C.240
41.(2019下·全国·六年级统考小升初模拟)水结成冰后体积会增加,那么冰化成水后体积会减少( )。
A. B. C. D.
42.(2022上·河南平顶山·六年级统考期末)刘叔叔去年使用微信消费1.8万元,__________。使用支付宝消费多少万元?如果用算式解决问题,横线上应补充下面信息( )。
A.使用微信消费比支付宝少 B.使用支付宝消费比微信少
C.使用支付宝消费是微信的 D.使用支付宝消费比微信多
43.(2022上·江苏淮安·六年级统考期末)在含盐率为20%的盐水中加入20克盐和20克水,盐水的浓度( )。
A.提高了 B.降低了 C.没有改变 D.无法确定
44.(2022上·江苏淮安·六年级统考期末)六(1)班星期一这天2人生病请假未到校,3人迟到,45人正常到校,六(1)班星期一这天的出勤率是( )%。
A.90% B.94% C.96% D.98%
45.(2022上·江苏宿迁·六年级统考期末)鲜蘑菇经晾干后减少原重量的85%,现有干蘑菇15千克,它是由多少千克鲜蘑菇晾干成的?列算式是( )。
A.15÷85% B.15×(1-85%) C.15÷(1-85%)
46.(2022上·江苏盐城·六年级统考期末)用4G下载一部《流浪地球》电影需要300秒,如果用5G下载所需时间约是4G的10%,只需( )秒。
A.50 B.30 C.0.03 D.15
47.(2022上·江苏宿迁·六年级统考期末)一杯糖水的含糖率是20%,加入6克糖和10克水后,这杯糖水的含糖率比原来( )。
A.提高了 B.降低了 C.不变
48.(2022上·江苏扬州·六年级统考期末)在含糖率8%的糖水中加入8克糖和100克水,现在糖水的含糖率( )。
A.变低了 B.变高了
C.不变 D.无法确定
49.(2022上·江苏盐城·六年级统考期末)一台电脑,将原标价先提价10%,再降价10%,结果两次调价后的价格比原来标价( )。
A.高 B.低 C.相等 D.无法比较
50.(2022上·江苏盐城·六年级统考期末)一杯糖水的含糖率是20%,喝去半杯后,含糖率是( )。
A.小于20% B.大于20% C.等于20% D.无法确定
参考答案:
1.C
【分析】减少的表面积就是重合的两个正方形的面积,用减少的表面积除以原来的表面积,即为表面积比原来减少了几分之几,据此解答。
【详解】1×1×2=2(平方分米)
2÷(1×1×6×2)
=2÷12
=
所以表面积比原来减少了。
故答案为:C
【点睛】解答本题的关键是明确减少的表面积也就是重合的两个正方形的面积。
2.C
【分析】求长方体盒子最多能放几个棱长是2厘米的正方体木块,就是求长方体的长、宽、高里分别有几个2厘米,用除法计算;再根据长方体的体积公式V=abh,把长、宽、高最多能放小正方体的个数相乘,即可求出小正方体的总个数。注意单位的换算:1分米=10厘米。
【详解】2分米=20厘米
20÷2=10(个)
6÷2=3(个)
5÷2=2(个)……1(厘米)
一共:10×3×2=60(个)
最多能放60个棱长是2厘米的正方体木块。
故答案为:C
【点睛】先分别求出长方体的长、宽、高最多能放几个小正方体,再利用长方体体积公式求出小正方体的总个数。
3.C
【分析】根据正方体的视图可知,带点的面和涂色面是相邻面,根据图形的折叠可知,选项A、D折成正方体后,带点的面和涂色面是相对面,B不是正方体的展开图,只有C折成正方体后,带点的面和涂色面是相邻面。据此判断即可。
【详解】根据正方体的视图可知,带点的面和涂色面是相邻面。
A.折成正方体后,带点的面和涂色面是相对面,不符合题意;
B.不是正方体的展开图,不符合题意;
C.折成正方体后,带点的面和涂色面是相邻面,符合题意;
D.折成正方体后,带点的面和涂色面是相对面,不符合题意。
故答案为:C
【点睛】此题考查了学生的空间想象能力以及对正方体展开图的熟练掌握程度。
4.D
【分析】根据长方体的高减少3厘米,就剩下一个正方体可知,这个正方体比原长方体表面积减少的高为3厘米的长方体的侧面积,即48平方厘米,则剩下的正方体的棱长为48÷4÷3=4厘米,原长方体的高为4+3=7厘米,再根据长方体的体积公式:V=abh,据此计算即可。
【详解】48÷4÷3
=12÷3
=4(厘米)
4+3=7(厘米)
4×4×7
=16×7
=112(立方厘米)
则原来长方体的体积是112立方厘米。
故答案为:D
【点睛】本题考查长方体的体积,求出原来长方体的长、宽和高是解题的关键。
5.B
【分析】根据体积、容积的意义,物体所占空间的大小叫做物体的体积,物体所容纳物体的体积叫做物体的容积。一个容器壁再薄也有厚度,因此,一个物体的容积要小于它的体积。根据长方体的体积=长×宽×高,用5×4×11即可求出长方体盒装的体积,它的容积比它的体积要小,据此解答。
【详解】5×4×11=220(立方厘米)
220立方厘米=220毫升
A.230毫升>220毫升
不符合题意;
B.200毫升<220毫升
符合题意;
C.120毫升<220毫升
120毫升太少,不符题意。
它所装酸奶的量比较合理的应该是200毫升。
故答案为:B
【点睛】本题主要是考查物体体积、容积的意义以及长方体体积公式的应用。物体体积、容积计算方法虽然相同。但度量时不同,计算体积从外面度量,计算容积从里面度量。
6.C
【分析】根据图意可知,从一个顶点处沿着长宽高挖掉一个小正方体,减少的面与增加的面个数是相等的都是3个面,所以长方体的表面积没发生变化。
【详解】因为在长方体的顶点上挖掉一个小正方体后,对于这个图形减少的面与增加的面个数是相等的都是3个,所以长方体的表面积没发生变化。
故答案为:C
【点睛】本题考查了关于长方体的表面积的问题,考查了学生观察,分析,解决问题的能力。
7.C
【分析】把这两块肥皂包装在一起,要想使表面积最小,那么应该把它们的最大的面相粘合,由此拼成的新长方体的长、宽、高分别是:7厘米、5厘米、6厘米,根据长方体的表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】把这两块肥皂包装在一起,拼成的新长方体的长、宽、高分别是:7厘米、5厘米、3×2=6(厘米)
(7×5+7×6+5×6)×2
=(35+42+30)×2
=(77+30)×2
=107×2
=214(平方厘米)
把长7厘米,宽5厘米,厚3厘米的长方体肥皂两块包装在一起,用214平方厘米包装纸最节省。
故答案为:C
【点睛】此题主要考查长方体的表面积公式的灵活运用;解答关键是理解:把它们的最大的面相粘合,包装最省纸。
8.C
【分析】根据题意可知:玻璃缸无论横放还是竖放水的体积不变,首先根据长方体的体积公式:体积=长×宽×高;求出玻璃缸内水的体积,然后用水的体积除以竖放时玻璃缸的底面积即可。
【详解】6×1×3÷(1×4)
=6×3÷4
=18÷4
=4.5(分米)
如果把缸竖起来,缸内水深4.5分米。
故答案为:C
【点睛】熟练掌握和灵活运用长方体体积公式是解答本题的关键。
9.B
【分析】把这根绳子的长度当作单位“1”,第一次剪去全长的,则剩下的占全长的(1-),即,因为 >,所以第二次不管剪去多少,都比第一次剪去的少。
【详解】1-=
>,第一次剪的长。
一根绳子,第一次剪去,第二次剪去米,两次剪去的长度相比,第一次长。
故答案为:B
【点睛】解答本题的关键是区分两个,一个是分率,一个是具体数量。
10.A
【分析】根据工作效率=工作量÷工作时间这一公式,分别算出甲、乙、丙三人的工作效率,再比较即可。
【详解】甲:3÷
=
=
乙:1÷
=1×6
=6
丙:5÷1=5
因为>6>5,所以丙的效率最甲。
故答案为:A
【点睛】此题考查了分数除法运算以及工作量、工作时间、工作效率三者之间的关系。
11.C
【分析】由题意可知,把梨的重量看作单位“1”,平均分成3份,其中的2份就是苹果的重量,即12千克,据此逐一分析各项即可。
【详解】A.表示把梨的重量看作单位“1”,平均分成3份,其中的2份就是苹果的重量,符合题意;
B.表示把梨的重量看作单位“1”,平均分成3份,其中的2份就是苹果的重量,符合题意;
C.表示把苹果的重量看作单位“1”,平均分成3份,其中的2份就是梨的重量,不符合题意;
D.表示把梨的重量看作单位“1”,平均分成3份,其中的2份就是苹果的重量,符合题意。
故答案为:C
【点睛】本题考查求一个数的几分之几是多少,明确单位“1”是解题的关键。
12.A
【分析】一个数(0除外)乘小于1的数,积比原来的数小。
分子比分母小的分数叫做真分数;真分数<1。
【详解】×<
则<1,那么b<a。
故答案为:A
【点睛】本题考查判断积与因数之间大小关系的方法以及真分数的认识。
13.A
【分析】根据倒数的意义,乘积是1的两个数互为倒数。求真分数和假分数的倒数时,把分子和分母调换位置即可,最后比较大小。
【详解】的倒数是;1的倒数是1;的倒数是;5的倒数是;
>1>>
的倒数是最大的。
故答案为:A
【点睛】此题考查的目的是理解倒数的意义,掌握求倒数的方法。
14.D
【分析】假设全班人数为30人,已知男生人数占全班人数的,则把全班人数看作单位“1”,根据分数乘法的意义,用30×即可求出男生人数,然后用全班人数减去男生人数,即可求出女生人数;求一个数比另一个数多几分之几,用相差数除以另一个数,则用男女生人数差除以女生人数,即可求出男生人数比女生人数多几分之几。
【详解】假设全班人数为30人,
男生:30×=16(人)
女生:30-16=14(人)
(16-14)÷14
=2÷14
=
男生人数比女生人数多。
故答案为:D
【点睛】本题主要考查了分数的应用,可用假设法解决问题,明确求一个数比另一个数多几分之几,用除法计算。
15.C
【分析】把甲仓库的吨数看作单位“1”,平均分成5份,每份是它的,把其中1份运给乙仓库,则两仓库存粮相等,说明甲仓库比乙仓库多这样的2份,乙仓库比甲仓库少2个,即,据此解答。
【详解】×2=
若把甲仓存粮的运给乙仓,则两仓存粮量相等,那么原来乙仓比甲仓少存。
故答案为:C
【点睛】本题考查分数的意义,关键明确:把甲仓库原来存粮的吨数平均分成5份,比乙仓库多2份,这两份就是。
16.A
【分析】把小强写的大字的个数看作单位“1”,是小丽写的大字占小强写的大字的分率,所以48×表示小丽写了多少个大字;据此选择即可。
【详解】8×表示小丽写了多少个大字。
故答案为:A。
【点睛】本题主要考查了分数乘法应用题,解题的关键是掌握:求一个数的几分之几是多少,用乘法计算。
17.A
【分析】根据倒数的意义可知,a×b=1,把a×b=1代入,计算即可。
【详解】
=
=
=
故答案为:A
【点睛】此题考查了用字母表示数、倒数的意义以及分数除法。
18.B
【分析】一个不为零的数乘上一个小于1的数,结果比原数小;一个不为零的数乘上一个大于1的数,结果比原数大。
【详解】A.因为,所以<a
B.=,因为,所以>a;
C.,因为,所以<a;
D.说法错误。
故答案为:B
【点睛】此题考查了积与乘数之间的关系。要求熟练掌握并灵活运用。
19.B
【分析】根据等腰三角形的两个底角相等,则等腰三角形的三个内角的度数比为1∶1∶2,再根据三角形的内角和是180°,根据按比例分配的方法,求出最大角的度数,再根据三角形按照角的大小分类情况进行判断即可。
【详解】180°÷(1+1+2)
=180°÷4
=45°
45°×2=90°
则有一个角是90度的三角形是直角三角形,所以这个三角形是直角三角形。
故答案为:B
【点睛】本题考查按比分配问题,结合等腰三角形的特征是解题的关键。
20.C
【分析】可以设4a=b=1,然后根据“因数=积÷另一个因数”,分别求出a、b的值,再根据比的意义写出a与b的比,最后化简比即可。
【详解】设4a=b=1。
a=1÷4=
b=1÷=1×=
a∶b
=∶
=(×4)∶(×4)
=1∶10
a与b的比是1∶10。
故答案为:C
【点睛】本题考查比的意义以及化简比,运用赋值法,根据乘法中各部分的关系计算出a、b的值是解题的关键。
21.B
【分析】根据题意,可以假设原来的含量为单位“1”,则5730年后为,9000大约是5720的1.5倍,不超过2倍。所以9000年后含有的量比÷2=×=多,比少。
【详解】设原来的含量为1,则5730年后为,所以9000年后含有的量比值在之间。
故答案为:B
【点睛】此题考查了分数的意义,要求熟练掌握并灵活运用。
22.B
【分析】已知加工一个零件要小时,求小时能加工多少个零件,就是求里面有几个,用除法计算。
【详解】÷
=×6
=3(个)
小时能加工3个零件。
解答正确的是:÷=3(个)
故答案为:B
【点睛】本题考查分数除法的应用,理解包含除法的意义是解题的关键。
23.D
【分析】将课桌价格看作单位“1”,一套课桌椅的价格是课桌价格的(1+),一套课桌椅的价格÷对应分率=课桌的价格,据此列式计算。
【详解】320÷(1+)
=320÷
=320×
=200(元)
课桌的价格是200元。
故答案为:D
【点睛】关键是确定单位“1”,理解分数除法的意义。
24.A
【分析】露出来的部分一样长,可设露出的长度为1,根据分数除法的意义分别求出四根绳子的长度再比较即可。
【详解】设露出的长度为1
A.1÷=1×6=6,A选项这根长为6;
B.1÷=1×5=5,B选项这根长为5;
C.1÷=1×4=4,C选项这根长为4;
D.1÷=1×3=3,D选项这根长为3;
6>5>4>3,所以A选项这根绳子最长。
故答案为:A
【点睛】本题主要考查分数除法的应用,明确已知量÷对应分率=表示单位“1”的量是解题的关键。
25.D
【分析】根据比的基本性质:比的前项和后项同时乘或除以一个不为0的数,比值不变;用3+6,再除以3,求出比的前项扩大到原来的多少倍,进而求出后项扩大到原来的多少倍,即可解答。
【详解】(3+6)÷3
=9÷3
=3
将3∶8的前项加上6,要使比值不变,后项应该乘3。
故答案为:D
【点睛】熟练掌握比的基本性质是解答本题的关键。
26.C
【分析】把甲地到乙地的路程看作单位“1”,先分别求出货车和客车的速度,进而写出货车和客车的速度比并化简比。
【详解】货车的速度:1÷4=
客车的速度:1÷6=
货车和客车速度比:∶
=(×12)∶(×12)
=3∶2
货车和客车速度比是3∶2
故答案为:C
【点睛】此题关键是先求出货车和客车的速度,进而写出货车和客车的速度比并化简比。
27.B
【分析】甲数的4倍与乙数的4倍的和是332,则甲数与乙数的和是332÷4=83。根据甲数比乙数多3,可设甲数是x,则乙数是x-3。再根据等量关系“甲数+乙数=83”列出方程,解方程可求出甲数。
【详解】解:设甲数是x。
x+(x-3)=332÷4
x+x-3=83
2x-3=83
2x=83+3
2x=86
x=86÷2
x=43
所以甲数是43。
故答案为:B
【点睛】已知两个数的和与差,可以用字母表示数,列方程解答。
28.B
【分析】观察左边图形可知,左上角托盘两个大黑球和一个小白球等于右上角托盘一个大黑球和四个小白球,托盘两边同时减去一个大黑球和一个小白球,结果是左上角托盘一个大黑球等于右上角托盘三个小白球,观察右边图形可知,左上角托盘里有两个小白球和一个大黑球,一个大黑球等于三个小白球,由此可知,右上角托盘应该放2+3=5个白球,据此解答。
【详解】根据分析可知,根据左边的天平,想一想,要使右边的天平平衡,在方框里只放白球,要放5个小白球。
故答案为:B
【点睛】解答本题的关键是找出大黑球与小白球之间的关系。
29.A
【分析】根据题意可知,每个茶杯的价格+30元=每个水瓶的价格,根据单价×数量=总价,用水瓶的单价×水瓶的数量+茶杯的单价×茶杯的数量=220元,据此设每个茶杯x元,列方程为:(x+30)×4+6x=220,然后解出方程即可。
【详解】解:设每个茶杯x元。
(x+30)×4+6x=220
4x+120+6x=220
10x+120=220
10x+120-120=220-120
10x=100
10x÷10=100÷10
x=10
每个茶杯10元。
故答案为:A
【点睛】本题可用列方程解决问题,找到相应的关系式是解答本题的关键。
30.A
【分析】根据题意可知,8块高钙饼干的钙含量=1杯牛奶的钙含量,12块高钙饼干的钙含量+1杯牛奶的钙含量=含钙600毫克,则(12+8)块高钙饼干的钙含量=含钙600毫克,用600÷(12+8)即可求出1块高钙饼干的钙含量,再乘8即可求出1杯牛奶的钙含量。
【详解】600÷(12+8)×8
=600÷20×8
=240(毫克)
一杯牛奶的钙含量是240毫克。
故答案为:A
【点睛】根据对应的等量代换找到合适的解题方法即可。
31.B
【分析】根据图形可知,3个杯子叠在一起的总高度是一个杯子的高度与2个杯口上升高度的和,5个杯子叠在一起的总高度是一个杯子的高度与4个杯口上升高度的和;用19减去15即为两个杯口上升的高度,用除法计算,即可求出一个杯口上升的高度,进而求出一个杯子的高度;根据总高度=一个杯口上升的高度×(杯子个数-1)+一个杯子的高度,用字母表示即可解答。
【详解】(19-15)÷(5-3)
=4÷2
=2(厘米)
15-2×2
=15-4
=11(厘米)
2×(a-1)+11
=2a-2+11
=9+2a(厘米)
如图,3个杯子叠起来高15厘米,5个杯子叠起来高19厘米。a个杯子叠起来的高度是9+2a厘米。
故答案为:B
【点睛】解答本题的关键是先计算出一个叠加部分的高度和最下面一个杯子的高度,最后计算出n个杯子叠加起来的高度。
32.C
【分析】先由图1可以得到一个较大圆=24克,再由图2可知,一个小圆为24×2÷3=16(克),由图3可知,最大圆为16×4=64(克),据此解答即可。
【详解】图1可以得到一个较大圆是24克
由图2可知,一个小圆是
24×2÷3
=48÷3
=16(克)
由图3可知,最大圆是
16×4=64(克)
故答案为:C
【点睛】由图1可以得到一个较大圆=24克,再求出小圆的值,是解答此题的关键。
33.C
【分析】假设都是兔,则应有35×4=140足,比实际多140-94=46足,多出的足数是将每只鸡的足数多算4-2=2足,故鸡有46÷2=23只,兔有35-23=12只;据此解答。
【详解】鸡:(35×4-94)÷(4-2)
=(140-94)÷2
=46÷2
=23(只)
兔:35-23=12(只)
故答案为:C
【点睛】本题主要考查鸡兔同笼问题,解答此类问题通常采用假设法。
34.A
【分析】由于要用替换的策略解决问题,想要求圆珠笔和钢笔的单价各是多少,已经有了钢笔和圆珠笔各自支数的总价,此时需要知道钢笔和圆珠笔的单价之间的关系,这样才可以用替换法解决,据此即可选择。
【详解】由分析可知:
一支圆珠笔比一支钢笔便宜3元,这是钢笔和圆珠笔之间的关系,其它条件不符合。
故答案为:A
【点睛】本题主要考查简单的等量代还的计算及应用,理解题意,找出数量关系。
35.C
【分析】在分数计算中,除以一个不为0的数等于乘它的倒数,这个算式可以运用乘法分配律a×c+b×c=(a+b)×c,因为+=1,方框中可以填的倒数即。
【详解】×+×=×+÷
填在算式×+÷□的方框中,这个算式就能简便计算。
故答案为:C
【点睛】本题主要考查了分数的简便运算,明确整数的运算律在分数中同样适用。
36.A
【分析】因为(a+)×3比a+×3多30,则可列方程为(a+)×3-(a+×3)=30,然后根据等式的性质解方程即可。
【详解】(a+)×3-(a+×3)=30
解:3a+×3-a-×3=30
2a=30
a=30÷2
a=15
a的值是15。
故答案为:A
【点睛】根据题意列出方程并熟练掌握分数乘法的运算定律是解答题目的关键。
37.B
【分析】把一桶油漆的重量看作单位“1”,已知用去,则剩下的重量占总重量的(1-),根据分数乘法的意义,用18×(1-)即可求出还剩多少千克。
【详解】18×(1-)
=18×
=3(千克)
还剩3千克。
故答案为:B
【点睛】本题主要考查了分数乘法的应用,明确求一个数的几分之几是多少,用乘法计算。
38.D
【分析】如果一个算式中只有加减法或者只有乘除法,要从左到右按顺序计算;如果算式中既有加减法,又有乘除法,要先算乘除法,后算加减法;如果算式中有括号,要先算括号里的;如果既有中括号又有小括号,要先算小括号里的,再算中括号里面的,据此解答。
【详解】根据运算顺序,在计算÷[+(1-)]时,先计算小括号里的减法,再计算中括号里的加法,最后计算括号外的除法,所以运算顺序是减→加→除。
故答案为:D
【点睛】熟练掌握分数四则混合运算顺序和运算法则是解答本题的关键。
39.B
【分析】可设甲绳长x米,乙绳长y米,甲绳先用去米,再用去剩下的;乙绳先用去,再用去米,可知甲剩下(x-)×(1-)米,乙剩下y×(1-)-米,因为两根绳子剩下的长度相等,即(x-)×(1-)=y×(1-)-,可通过计算,得出x与y之间的关系,进而解答。
【详解】解:设甲绳长x米,乙绳长y米,根据题意可得:
(x-)×(1-)=y×(1-)-
(x-)×=y-
x-=y-
y-x=-
y-x=-
y-x=
9y-90x=1
90(y-x)=1
y-x=1÷90
y-x=
y>x,即乙绳长>甲绳长。
有甲、乙两根绳子,甲绳先用去米,再用去剩下的;乙绳先用去,再用去米,结果两根绳子剩下的长度相等,原来两根绳子相比,乙绳长。
故答案为:B
【点睛】理解数量米和分数的不同,找出甲、乙两根绳子剩下部分的等量关系是解答本题的关键。
40.C
【分析】由题意可知:女生人数不变,先将原来的学生人数看成单位“1”,根据分数乘法的意义,用600×求出女生人数;再将现在的人数看成单位“1”,根据分数除法的意义,用女生人数÷现在的分率,求出现在的人数,最后用现在人数-原来人数求出转来男生的人数。
【详解】600×÷-600
=350÷-600
=350×-600
=840-600
=240(人)
转来男生240人。
故答案为:C
【点睛】本题考查“求一个数的几分之几”及“已知一个数的几分之几是多少求这个数”的简单运用。
41.D
【分析】设水的体积是1;把水的体积看作单位“1”,则冰的体积是水的体积的(1+),再用水的体积×(1+),求出冰的体积,再用冰与水的体积差,除以冰的体积,即可求出冰化成水后体积会减少的分率;据此解答。
【详解】设水的体积是1。
1×(1+)
=1×
=
(-1)÷
=×
=
水结成冰后体积会增加,那么冰化成水后体积会减少。
故答案为:D
【点睛】解决此题关键是找准单位“1”,水结成冰,水的体积是单位“1”;冰化成水,冰的体积是单位“1”。
42.A
【分析】求一个数的几分之几是多少用乘法;已知一个数的几分之几是多少,求这个数用除法;据此逐项分析各选项即可。
【详解】A.使用微信消费比支付宝少,是将使用支付宝消费的钱数看成单位“1”,使用微信消费比支付宝少,则使用微信消费是支付宝的1-,求使用支付宝消费的钱数,用1.8÷(1-)计算,该选项符合题意;
B.使用支付宝消费比微信少,是将使用微信消费的钱数看成单位“1”,使用支付宝消费比微信少,则使用支付宝消费是微信的1-,求使用支付宝消费的钱数,用1.8×(1-)计算,该选项不符合题意;
C.使用支付宝消费是微信的,是将微信消费钱数看成单位“1”,求使用支付宝消费钱数,用1.8×计算,该选项不符合题意;
D.使用支付宝消费比微信多,是将微信消费钱数看成单位“1”,使用支付宝消费的钱数是微信的1+,求使用支付宝消费的钱数,用1.8×(1+)计算,该选项不符合题意;
故答案为:A
【点睛】熟练掌握求比一个数多\少几分之几的数是多少及已知比一个数多/少几分之几的数是多少,求这个数的解题方法是解题的关键。
43.A
【分析】根据含盐率=盐的重量÷盐水的重量×100%,已知盐重20克,水重20克,则盐水重20+20=40克,可求出加入盐水的含盐率,再同原来盐水的含盐率进行比较,若加入盐水的含盐率高于原来的含盐率,盐水的浓度就提高了,反之就降低了。
【详解】20÷(20+20)×100%
=20÷40×100%
=0.5×100%
=50%
50%>20%
则在含盐率为20%的盐水中加入20克盐和20克水,盐水的浓度提高了。
故答案为:A
【点睛】本题考查含盐率,明确含盐率的计算方法是解题的关键。
44.C
【分析】根据题意,先用正常到校的人数加上请病假的人数,再加上迟到的人数,求出六(1)班的总人数;用正常到校人数加上迟到人数,求出六(1)班今天出勤的人数。
再根据“出勤率=出勤的人数÷总人数×100%”,代入数据计算,即可求解。
【详解】(45+3)÷(45+2+3)×100%
=48÷50×100%
=0.96×100%
=96%
六(1)班星期一这天的出勤率是96%。
故答案为:C
【点睛】本题考查百分率问题,掌握出勤率的意义及计算方法是解题的关键。
45.C
【分析】根据题意,干蘑菇的质量比鲜蘑菇的质量少85%,那么干蘑菇的质量是鲜蘑菇质量的(1-85%)。将鲜蘑菇的质量看作单位“1”,单位“1”未知,用干蘑菇质量除以(1-85%),即可求出它是由多少千克鲜蘑菇晾干成的。
【详解】求15千克干蘑菇是由多少千克鲜蘑菇晾干成的?列算式是15÷(1-85%)。
故答案为:C
【点睛】本题考查了含百分数的运算,已知比一个数少百分之几的数是多少,求这个数用除法。
46.B
【分析】根据题意,可以用300乘上10%即可算出答案。
【详解】300×10%=30(秒),只需30秒。
故答案为:B
【点睛】此题考查了百分数的应用,要求熟练掌握并灵活运用。
47.A
【分析】用6克糖除以(6+10)克糖水,求出加入部分糖水的含糖率。如果它比原来的含糖率高,则最终整杯糖水的含糖率比原来就提高了。反之则降低,据此解题。
【详解】6÷(6+10)
=6÷16
=37.5%
37.5%>20%,所以加入6克糖和10克水后,这杯糖水的含糖率比原来提高了。
故答案为:A
【点睛】本题考查了百分率问题,求一个数是另一个数的百分之几,用这个数除以另一个数。
48.A
【分析】含糖率表示糖的质量占糖水质量的百分之几,计算方法:含糖率=糖的质量÷糖水的质量×100%,由此求出加入的糖水的含糖率,与原来的含糖率相比较,得出结论。
【详解】加入的糖水的含糖率:
8÷(8+100)×100%
=8÷108×100%
≈0.074×100%
=7.4%
7.4<8%
现在糖水的含糖率变低了。
故答案为:A
【点睛】本题考查百分率问题,掌握含糖率的意义及计算方法是解题的关键。
49.B
【分析】设这台电脑的原价是1,先提价10%,是把原价看作单位“1”,则提价后的价格是原价的(1+10%),单位“1”已知,根据百分数乘法的意义求出提价后的价格;
再降价10%,是把提价后的价格看作单位“1”,则降价后的价格是提价后价格的(1-10%);单位“1”已知,用乘法求出现价,再与原价相比较,得出结论。
【详解】设这台电脑的原价是1。
1×(1+10%)×(1-10%)
=1×1.1×0.9
=0.99
0.99<1
结果两次调价后的价格比原来标价低。
故答案为:B
【点睛】本题考查百分数乘法的应用,区分两个单位“1”的不同,明确求比一个数多或少百分之几的数是多少,用乘法计算。
50.C
【分析】含糖20%的糖水,喝去半杯后,剩下的糖水并没有加水,也没有加糖,因此含糖率不变,还是20%,据此分析。
【详解】根据分析,一杯糖水的含糖率是20%,喝去半杯后,含糖率不变,还是等于20%。
故答案为:C
【点睛】关键是理解百分率的意义,掌握百分率的求法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
