数学人教A版(2019)必修第一册3.1.2函数的表示法 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.1.2函数的表示法 课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 07:25:57 | ||
图片预览






文档简介
(共20张PPT)
高中数学人教A版必修一
3.1.2 函数的表示法
1.函数三要素:定义域、对应关系和值域.
2.函数三种表示法:解析法、列表法和图象法.
回顾旧知
问题1 某“复兴号”高速列车加速到后保持匀速运行半小时.这段时间内,列车行进的路程(单位:km)与运行时间(单位:h)的关系可以表示为:
解析式
.
学习探究一:函数的表示法
用数学表达式表示两个变量之间的对应关系的方法叫做解析法.
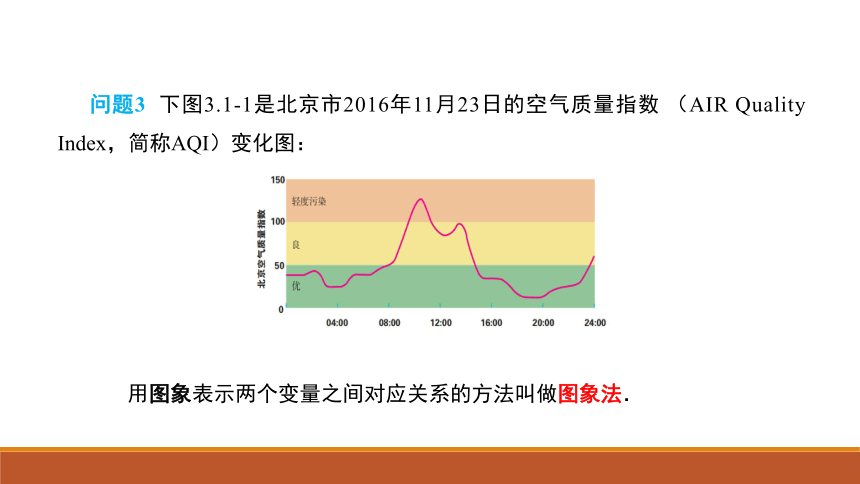
问题3 下图3.1-1是北京市2016年11月23日的空气质量指数 (AIR Quality Index,简称AQI)变化图:
用图象表示两个变量之间对应关系的方法叫做图象法.
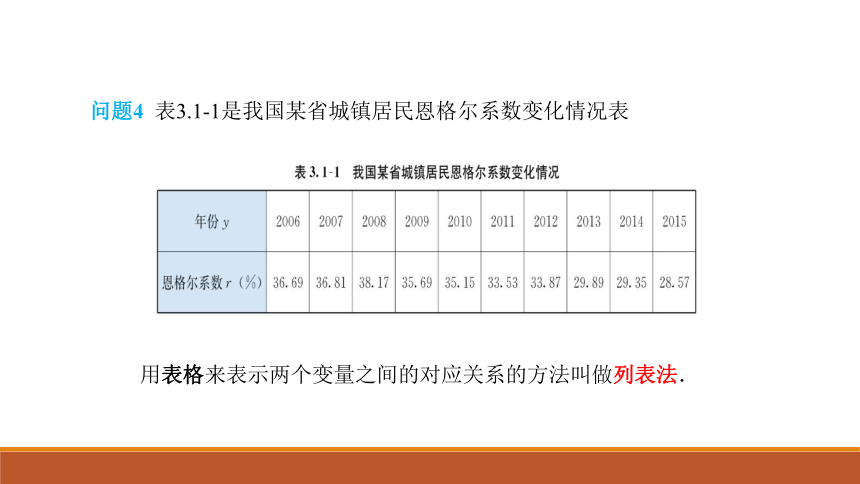
问题4 表3.1-1是我国某省城镇居民恩格尔系数变化情况表
用表格来表示两个变量之间的对应关系的方法叫做列表法.
总结:函数的三种表示法各自的特点是什么?
表示法 优点 缺点
解析法 简明、全面地概括了变量间的关系;可以通过解析式求出任意一个自变量的值所对应的函数值 不够形象直观,而且并不是所有的函数都有解析式
图象法 形象、直观地表示自变量变化情况 只能近似的求出自变量所对应的函数值,有时误差较大
列表法 直观、离散,不需要计算就可以直接看出与自变量的值对应的函数值 只能表示有限个数的自变量所对应的函数值
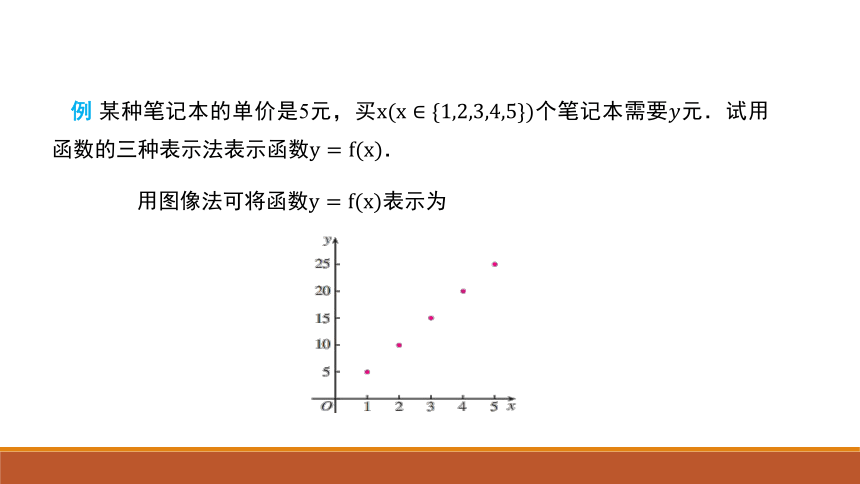
例 某种笔记本的单价是5元,买个笔记本需要元.试用函数的三种表示法表示函数.
解:这个函数的定义域是数集
用列表法可将函数表示为
用解析法可将函数表示为
.
用图像法可将函数表示为
例 某种笔记本的单价是5元,买个笔记本需要元.试用函数的三种表示法表示函数.
【思考】
(1)所有函数都能用解析法表示吗?图像法和列表法呢?
(2)函数的图像可以是哪些形状?任意图像是函数的图像吗?
例1 已知函数,分别由下表给出:
则 ;当时,= .
1 2 3
2 1 1
3 2 1
[变式] 在本例已知条件下,= ;当时,x= .
1
1
2
3
学习探究二:列表法表示函数
学习探究三:函数图像及其应用
例3 函数的图像如下图,则的定义域是 ,值域是 .
一、“看”函数图像
例2 下图中哪几个图象与下述三件事分别吻合得最好?(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;(2)我骑着车离开家后一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)我从家出发后,心情轻松,一路缓缓加速行进.
二、“用”函数图像
函数解析式 图像 一次函数
反比例函数 二次函数
图像
定义域
值域
对称轴
顶点坐标
例4 作出下列函数的简图,并根据图像写出其值域:
(1);
解: 当,图像是直线的一部分.
如图所示,
观察图像可知,函数的值域为
(2);
解: 当,图像是反比例函数的一部分.
如图所示,
观察图像可知,函数的值域为
(3)2.
解: 当,图像是抛物线的一部分.
如图所示,
观察图像可知,函数的值域为
数缺形时少直观
形少数时难入微
数形结合百般好
隔离分家万事非
——华罗庚
解 是抛物线去掉之间
的部分后剩余的曲线.
如图所示,
观察图像可知,函数的值域为
[变式] 已知函数 ,求函数 的值域.
1. 内容上:
解析法 列表法 图象法
1.简明 2.抽象 直观 1.直观形象
2.变化趋势
1.有规律 2.不直观 1.离散 2.“少” 1.不精准
2.不全面
课堂小结
2. 思想方法上:
课堂小结:
数形结合
以形化数+以数辅形.
数缺形时少直观
形少数时难入微
数形结合百般好
隔离分家万事非
——华罗庚
高中数学人教A版必修一
3.1.2 函数的表示法
1.函数三要素:定义域、对应关系和值域.
2.函数三种表示法:解析法、列表法和图象法.
回顾旧知
问题1 某“复兴号”高速列车加速到后保持匀速运行半小时.这段时间内,列车行进的路程(单位:km)与运行时间(单位:h)的关系可以表示为:
解析式
.
学习探究一:函数的表示法
用数学表达式表示两个变量之间的对应关系的方法叫做解析法.
问题3 下图3.1-1是北京市2016年11月23日的空气质量指数 (AIR Quality Index,简称AQI)变化图:
用图象表示两个变量之间对应关系的方法叫做图象法.
问题4 表3.1-1是我国某省城镇居民恩格尔系数变化情况表
用表格来表示两个变量之间的对应关系的方法叫做列表法.
总结:函数的三种表示法各自的特点是什么?
表示法 优点 缺点
解析法 简明、全面地概括了变量间的关系;可以通过解析式求出任意一个自变量的值所对应的函数值 不够形象直观,而且并不是所有的函数都有解析式
图象法 形象、直观地表示自变量变化情况 只能近似的求出自变量所对应的函数值,有时误差较大
列表法 直观、离散,不需要计算就可以直接看出与自变量的值对应的函数值 只能表示有限个数的自变量所对应的函数值
例 某种笔记本的单价是5元,买个笔记本需要元.试用函数的三种表示法表示函数.
解:这个函数的定义域是数集
用列表法可将函数表示为
用解析法可将函数表示为
.
用图像法可将函数表示为
例 某种笔记本的单价是5元,买个笔记本需要元.试用函数的三种表示法表示函数.
【思考】
(1)所有函数都能用解析法表示吗?图像法和列表法呢?
(2)函数的图像可以是哪些形状?任意图像是函数的图像吗?
例1 已知函数,分别由下表给出:
则 ;当时,= .
1 2 3
2 1 1
3 2 1
[变式] 在本例已知条件下,= ;当时,x= .
1
1
2
3
学习探究二:列表法表示函数
学习探究三:函数图像及其应用
例3 函数的图像如下图,则的定义域是 ,值域是 .
一、“看”函数图像
例2 下图中哪几个图象与下述三件事分别吻合得最好?(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;(2)我骑着车离开家后一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)我从家出发后,心情轻松,一路缓缓加速行进.
二、“用”函数图像
函数解析式 图像 一次函数
反比例函数 二次函数
图像
定义域
值域
对称轴
顶点坐标
例4 作出下列函数的简图,并根据图像写出其值域:
(1);
解: 当,图像是直线的一部分.
如图所示,
观察图像可知,函数的值域为
(2);
解: 当,图像是反比例函数的一部分.
如图所示,
观察图像可知,函数的值域为
(3)2.
解: 当,图像是抛物线的一部分.
如图所示,
观察图像可知,函数的值域为
数缺形时少直观
形少数时难入微
数形结合百般好
隔离分家万事非
——华罗庚
解 是抛物线去掉之间
的部分后剩余的曲线.
如图所示,
观察图像可知,函数的值域为
[变式] 已知函数 ,求函数 的值域.
1. 内容上:
解析法 列表法 图象法
1.简明 2.抽象 直观 1.直观形象
2.变化趋势
1.有规律 2.不直观 1.离散 2.“少” 1.不精准
2.不全面
课堂小结
2. 思想方法上:
课堂小结:
数形结合
以形化数+以数辅形.
数缺形时少直观
形少数时难入微
数形结合百般好
隔离分家万事非
——华罗庚
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
