1.3专题:找圆心定半径,求角度求时间课件 (共32张PPT) 高二下学期物理人教版(2019)选择性必修第二册
文档属性
| 名称 | 1.3专题:找圆心定半径,求角度求时间课件 (共32张PPT) 高二下学期物理人教版(2019)选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-26 22:00:14 | ||
图片预览




文档简介
(共32张PPT)
1.3 带电粒子在匀强磁场中的运动
第2课时 圆周运动圆心、半径、时间的确定
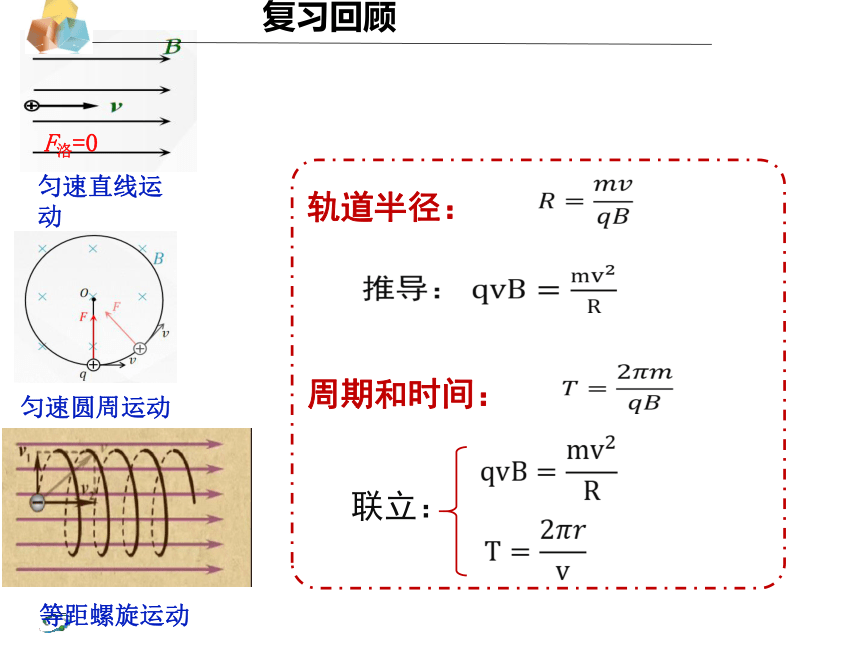
匀速圆周运动
F洛=0
匀速直线运动
等距螺旋运动
复习回顾
复习回顾
轨道半径:
周期和时间:
推导:
联立:
V0
P
M
O
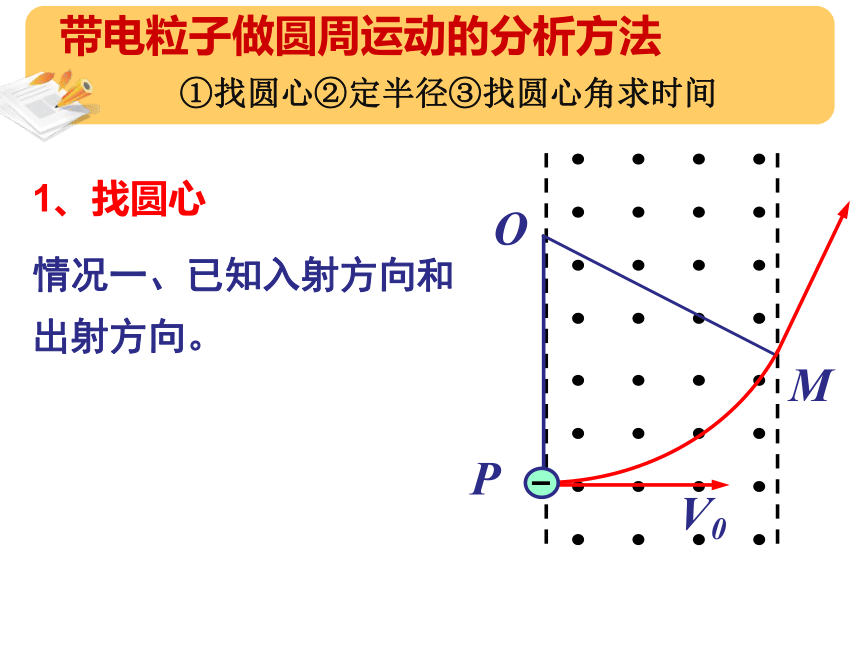
情况一、已知入射方向和出射方向。
1、找圆心
带电粒子做圆周运动的分析方法
-圆心的确定
带电粒子做圆周运动的分析方法
①找圆心②定半径③找圆心角求时间
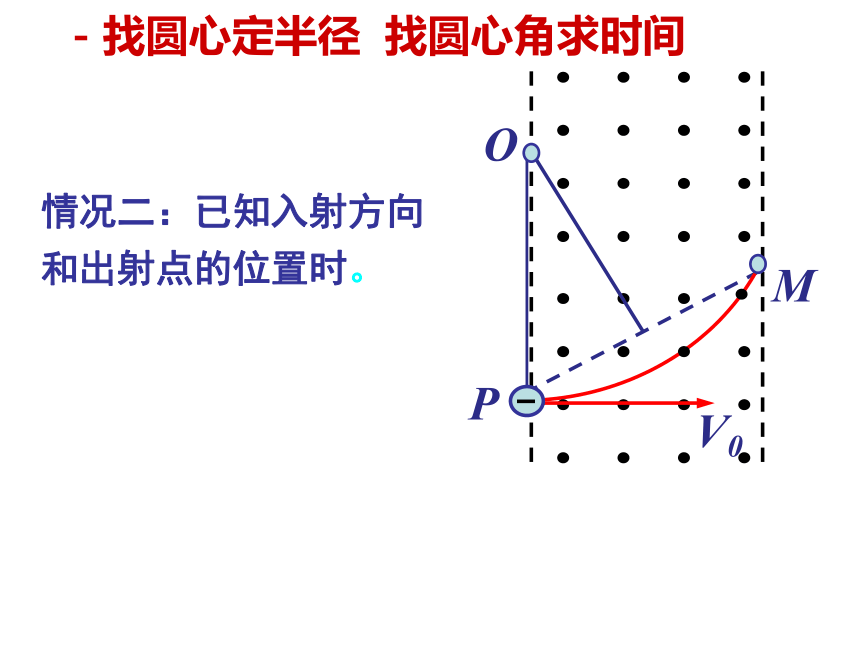
情况二:已知入射方向和出射点的位置时。
P
M
V0
O
-找圆心定半径 找圆心角求时间
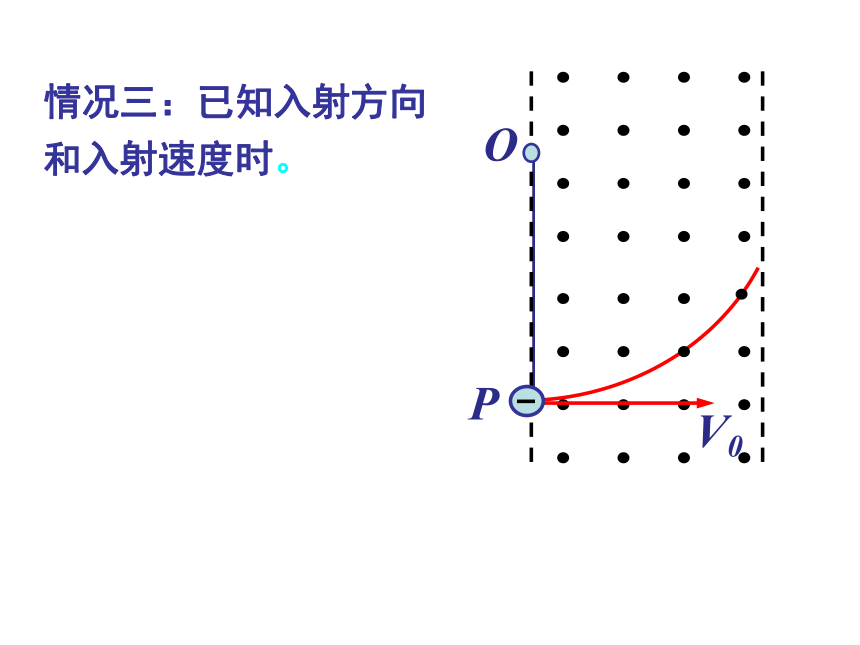
情况三:已知入射方向和入射速度时。
P
V0
O
情况四:圆周上3个点时。
③已知圆周上3个点的位置
●
●
●
A
B
C
(1)公式法:
(2)几何方法:
2、定半径
带电粒子做圆周运动的分析方法
-圆心的确定
二、带电粒子做圆周运动的分析方法
-找圆心定半径
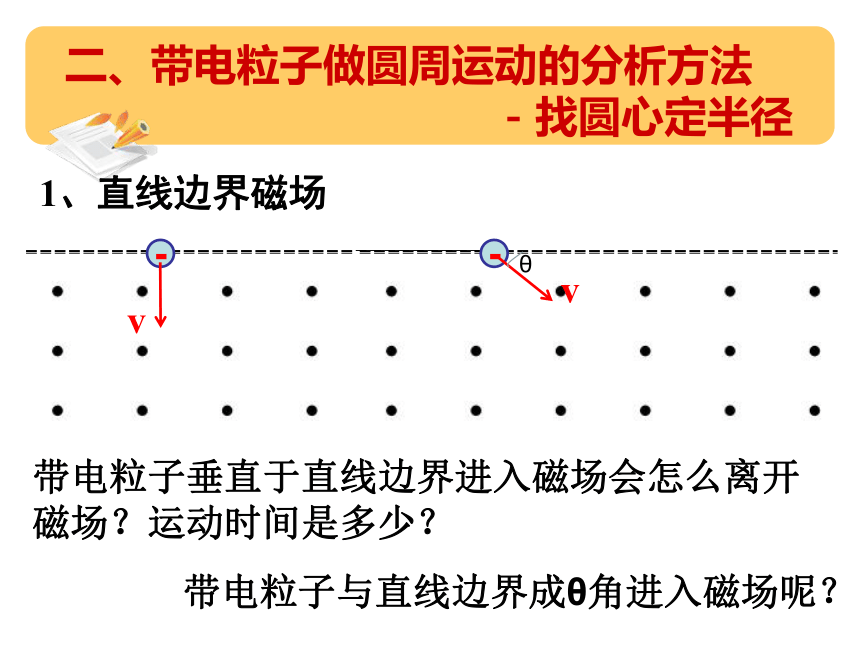
1、直线边界磁场
-
v
带电粒子垂直于直线边界进入磁场会怎么离开磁场?运动时间是多少?
-
v
θ
带电粒子与直线边界成θ角进入磁场呢?
当带电粒子从同一边界入射出射时速度与边界夹角相同
——对称性
常见的几种情形
[多少度进多少度出]
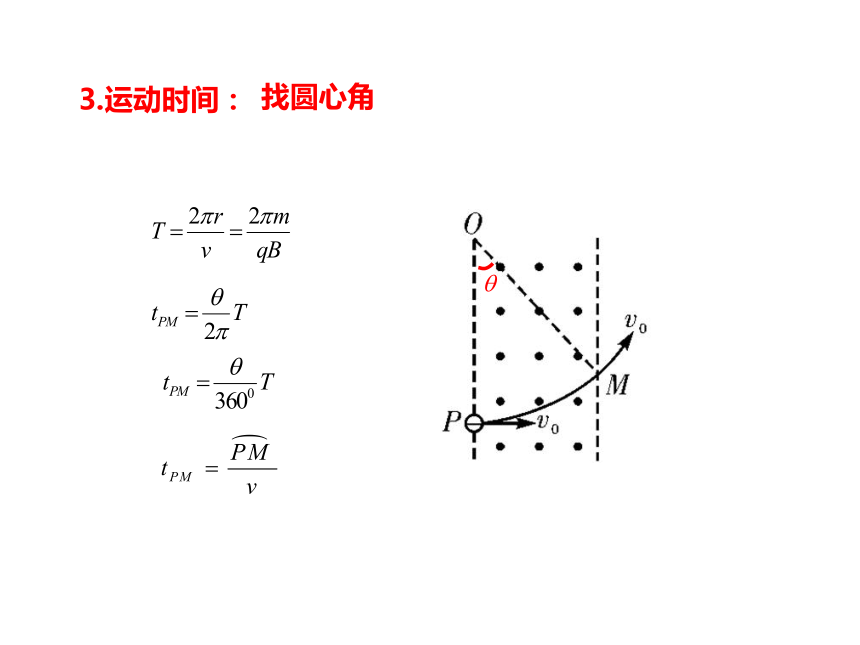
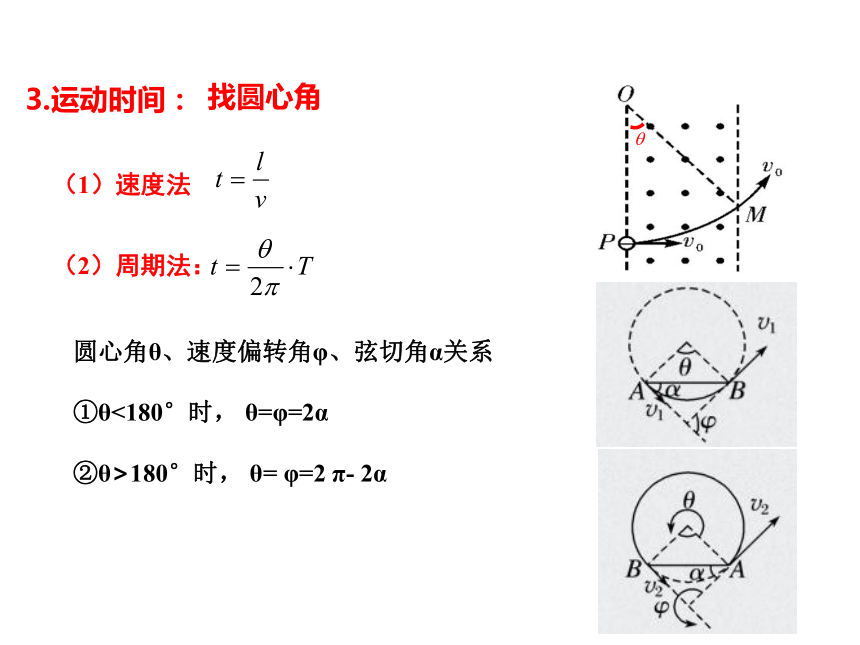
3.运动时间:
找圆心角
(2)周期法:
(1)速度法
圆心角θ、速度偏转角φ、弦切角α关系
①θ<180°时, θ=φ=2α
②θ>180°时, θ= φ=2 π- 2α
3.运动时间:
找圆心角
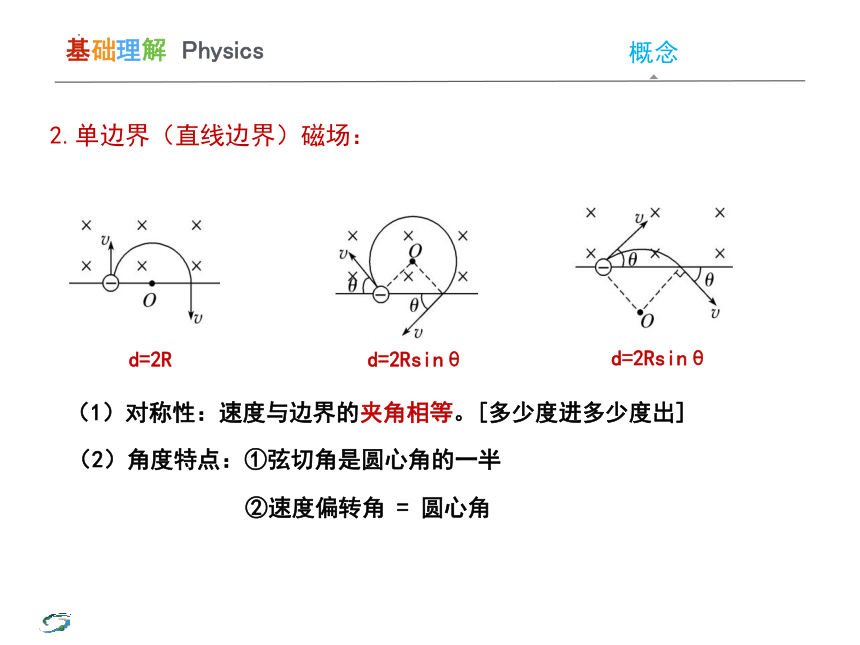
2.单边界(直线边界)磁场:
(1)对称性:速度与边界的夹角相等。[多少度进多少度出]
d=2R
d=2Rsinθ
d=2Rsinθ
(2)角度特点:①弦切角是圆心角的一半
②速度偏转角 = 圆心角
二、带电粒子在有界磁场中的运动
1、直线边界磁场(进出磁场具有对称性)
2、平行边界
V0
P
(存在临界条件)
v0小?v0大?
+
4.平行边界(双边有界):存在临界条件
d=R1(1-cosθ)
或 d=2R2
d=R(1+cosθ)
d=R(1-cosθ)
一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?
先确定圆心在虚线上,分别画出半径逐渐增大的轨迹图
图1
图2
图3
图4
图5
①图1至图3 ,v增大,r增大,图1至图3均从左边界飞出,但图3速度恰好与右边界相切,是临界状态。
②v继续增大,r增大,如图5,粒子从右边界飞出。
关键:找出临界状态:速度方向与右边界相切
二、带电粒子在有界磁场中的运动
1、直线边界磁场(进出磁场具有对称性)
2、平行边界
(存在临界条件)
3、圆形边界磁场(沿径向射入
+
v
必沿径向射出)
(2)若沿各方向射入时,
①最大半径:
②最大速率:
(1)若沿区域圆半径方向射入时,
①最大半径:
②最大速率:
(径向射入环形匀强磁场中,恰好不能从磁场中出射时)
环形边界磁场:
8.如图所示,两匀强磁场的方向相同,以虚线MN为理想边界,磁感应强度大小分别为B1、B2,一质量为m、电荷量为e的电子从MN上的P点沿垂直于磁场方向射入匀强磁场B1中,其运动轨迹为如图虚线所示的“心”形图线.则以下说法正确的是 ( )
【答案】B
例: 质量为m,电荷量为q的粒子,以初速度v0垂直进入磁感应强度为B、宽度为L的匀强磁场区域,如图所示。求
(1)带电粒子的运动轨迹及运动性质
(2)带电粒子运动的轨道半径
(3)带电粒子离开磁场时的速率
(4)带电粒子离开磁场时的偏转角θ
(5)带电粒子在磁场中的运动时间 t
d
B
e
θ
v
如图所示,一束电子(电量为e)以速度v垂直射入磁感应强度为B、宽度为d的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角为300。求 :
(1)求轨道半径
(2) 电子的质量m=
(3) 电子在磁场中的运动时间t=
解:(1)由题意得电子的运动轨迹,如图所示
由几何关系得:
B
(3)因圆心角是30°,所以穿过磁场的时间为
(2)由洛沦兹力提供向心力得:
解得:
v
d
e
θ
v
θ
练习1. 如图,水平导线中有电流I通过,导线正下方的电子初速度的方向与电
流I的方向相同,则电子将( )
A. 沿路径a运动,轨迹是圆
B. 沿路径a运动,轨迹半径越来越大
C. 沿路径a运动,轨迹半径越来越小
D. 沿路径b运动,轨迹半径越来越大
v
a
b
I
B
x
y
o
p
θ
v
θ
θ
v
θ
如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸面外,磁感应强度为B。一带正电的粒子以速度v0从O点射入磁场,入射方向在x0y平面内,与x轴正向的夹角为θ。若粒子射出磁场的位置与O点的距离为L,求该粒子的比荷q/m。
·
解:
由牛顿第二定律得
由几何知识得,
由上两式可得粒子的荷质比:
设P点为出射点,作出粒子运动轨迹如图,
如图所示,长为L的水平极板间,有垂直纸面向里的匀强磁场,磁感应强度为B,板间距离也为L,板不带电,现有质量为m、电量为q的带正电粒子(不计重力)从左边极板间中点处垂直磁感线以速度v水平射入磁场,为使粒子能够打在极板上,则粒子的速度应满足什么关系?
L
a
b
解:经分析得,粒子打在b点时有最大速度vmax,打在
a点时有最小速度vmin。
当粒子打在b点时,设对应的半径为R,则由几何知识可得:
如图所示作辅助线。
解得:
所以
a
b
o
R
R-L/2
L
当粒子打在a点时,设对应的半径为r
则由几何知识可得
所以最小速度为
故粒子的速度应满足
a
b
o
R
R-L/2
L
两个质量和电荷量都相同的带电粒子a、b,以不同的
速率对准圆心O沿着AO方向射入圆形匀强磁场区域,
其运动轨迹如图.若不计粒子的重力,则下列说法正
确的是( )(多选)
A.粒子都带负电
B.b粒子速率较大
C.b粒子在磁场中运动时间较长
D.它们做圆周运动的周期Ta=Tb
O
a
b
Ob
Oa
θb
θa
A
BD
轨道半径r跟运动速率成正比,
周期T与半径和速率无关
运动时间t由圆心角决定
如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力。求:
(1)电子在磁场中运动轨迹的半径R;
(2)电子在磁场中运动的时间t;
(3)圆形磁场区域的半径r。
B
O
v
v
θ
r
解:
(1)由牛顿第二定律和洛伦兹力公式得
解得:
(2)设电子做匀速圆周运动的周期为T,
则
由如图所示的几何关系得
所以
(3)由如图所示几何关系可知,
O1
v
B
R
O
v
θ
r
r
R
1.3 带电粒子在匀强磁场中的运动
第2课时 圆周运动圆心、半径、时间的确定
匀速圆周运动
F洛=0
匀速直线运动
等距螺旋运动
复习回顾
复习回顾
轨道半径:
周期和时间:
推导:
联立:
V0
P
M
O
情况一、已知入射方向和出射方向。
1、找圆心
带电粒子做圆周运动的分析方法
-圆心的确定
带电粒子做圆周运动的分析方法
①找圆心②定半径③找圆心角求时间
情况二:已知入射方向和出射点的位置时。
P
M
V0
O
-找圆心定半径 找圆心角求时间
情况三:已知入射方向和入射速度时。
P
V0
O
情况四:圆周上3个点时。
③已知圆周上3个点的位置
●
●
●
A
B
C
(1)公式法:
(2)几何方法:
2、定半径
带电粒子做圆周运动的分析方法
-圆心的确定
二、带电粒子做圆周运动的分析方法
-找圆心定半径
1、直线边界磁场
-
v
带电粒子垂直于直线边界进入磁场会怎么离开磁场?运动时间是多少?
-
v
θ
带电粒子与直线边界成θ角进入磁场呢?
当带电粒子从同一边界入射出射时速度与边界夹角相同
——对称性
常见的几种情形
[多少度进多少度出]
3.运动时间:
找圆心角
(2)周期法:
(1)速度法
圆心角θ、速度偏转角φ、弦切角α关系
①θ<180°时, θ=φ=2α
②θ>180°时, θ= φ=2 π- 2α
3.运动时间:
找圆心角
2.单边界(直线边界)磁场:
(1)对称性:速度与边界的夹角相等。[多少度进多少度出]
d=2R
d=2Rsinθ
d=2Rsinθ
(2)角度特点:①弦切角是圆心角的一半
②速度偏转角 = 圆心角
二、带电粒子在有界磁场中的运动
1、直线边界磁场(进出磁场具有对称性)
2、平行边界
V0
P
(存在临界条件)
v0小?v0大?
+
4.平行边界(双边有界):存在临界条件
d=R1(1-cosθ)
或 d=2R2
d=R(1+cosθ)
d=R(1-cosθ)
一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?
先确定圆心在虚线上,分别画出半径逐渐增大的轨迹图
图1
图2
图3
图4
图5
①图1至图3 ,v增大,r增大,图1至图3均从左边界飞出,但图3速度恰好与右边界相切,是临界状态。
②v继续增大,r增大,如图5,粒子从右边界飞出。
关键:找出临界状态:速度方向与右边界相切
二、带电粒子在有界磁场中的运动
1、直线边界磁场(进出磁场具有对称性)
2、平行边界
(存在临界条件)
3、圆形边界磁场(沿径向射入
+
v
必沿径向射出)
(2)若沿各方向射入时,
①最大半径:
②最大速率:
(1)若沿区域圆半径方向射入时,
①最大半径:
②最大速率:
(径向射入环形匀强磁场中,恰好不能从磁场中出射时)
环形边界磁场:
8.如图所示,两匀强磁场的方向相同,以虚线MN为理想边界,磁感应强度大小分别为B1、B2,一质量为m、电荷量为e的电子从MN上的P点沿垂直于磁场方向射入匀强磁场B1中,其运动轨迹为如图虚线所示的“心”形图线.则以下说法正确的是 ( )
【答案】B
例: 质量为m,电荷量为q的粒子,以初速度v0垂直进入磁感应强度为B、宽度为L的匀强磁场区域,如图所示。求
(1)带电粒子的运动轨迹及运动性质
(2)带电粒子运动的轨道半径
(3)带电粒子离开磁场时的速率
(4)带电粒子离开磁场时的偏转角θ
(5)带电粒子在磁场中的运动时间 t
d
B
e
θ
v
如图所示,一束电子(电量为e)以速度v垂直射入磁感应强度为B、宽度为d的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角为300。求 :
(1)求轨道半径
(2) 电子的质量m=
(3) 电子在磁场中的运动时间t=
解:(1)由题意得电子的运动轨迹,如图所示
由几何关系得:
B
(3)因圆心角是30°,所以穿过磁场的时间为
(2)由洛沦兹力提供向心力得:
解得:
v
d
e
θ
v
θ
练习1. 如图,水平导线中有电流I通过,导线正下方的电子初速度的方向与电
流I的方向相同,则电子将( )
A. 沿路径a运动,轨迹是圆
B. 沿路径a运动,轨迹半径越来越大
C. 沿路径a运动,轨迹半径越来越小
D. 沿路径b运动,轨迹半径越来越大
v
a
b
I
B
x
y
o
p
θ
v
θ
θ
v
θ
如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸面外,磁感应强度为B。一带正电的粒子以速度v0从O点射入磁场,入射方向在x0y平面内,与x轴正向的夹角为θ。若粒子射出磁场的位置与O点的距离为L,求该粒子的比荷q/m。
·
解:
由牛顿第二定律得
由几何知识得,
由上两式可得粒子的荷质比:
设P点为出射点,作出粒子运动轨迹如图,
如图所示,长为L的水平极板间,有垂直纸面向里的匀强磁场,磁感应强度为B,板间距离也为L,板不带电,现有质量为m、电量为q的带正电粒子(不计重力)从左边极板间中点处垂直磁感线以速度v水平射入磁场,为使粒子能够打在极板上,则粒子的速度应满足什么关系?
L
a
b
解:经分析得,粒子打在b点时有最大速度vmax,打在
a点时有最小速度vmin。
当粒子打在b点时,设对应的半径为R,则由几何知识可得:
如图所示作辅助线。
解得:
所以
a
b
o
R
R-L/2
L
当粒子打在a点时,设对应的半径为r
则由几何知识可得
所以最小速度为
故粒子的速度应满足
a
b
o
R
R-L/2
L
两个质量和电荷量都相同的带电粒子a、b,以不同的
速率对准圆心O沿着AO方向射入圆形匀强磁场区域,
其运动轨迹如图.若不计粒子的重力,则下列说法正
确的是( )(多选)
A.粒子都带负电
B.b粒子速率较大
C.b粒子在磁场中运动时间较长
D.它们做圆周运动的周期Ta=Tb
O
a
b
Ob
Oa
θb
θa
A
BD
轨道半径r跟运动速率成正比,
周期T与半径和速率无关
运动时间t由圆心角决定
如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力。求:
(1)电子在磁场中运动轨迹的半径R;
(2)电子在磁场中运动的时间t;
(3)圆形磁场区域的半径r。
B
O
v
v
θ
r
解:
(1)由牛顿第二定律和洛伦兹力公式得
解得:
(2)设电子做匀速圆周运动的周期为T,
则
由如图所示的几何关系得
所以
(3)由如图所示几何关系可知,
O1
v
B
R
O
v
θ
r
r
R
