第四章锐角三角形单元测试卷(含解析)

中小学教育资源及组卷应用平台
2023-2024学年 湘教版（2012）九年级上册 第四章 锐角三角形 单元测试卷
学校:___________姓名：___________班级：___________考号：___________
评卷人得分
一、单选题
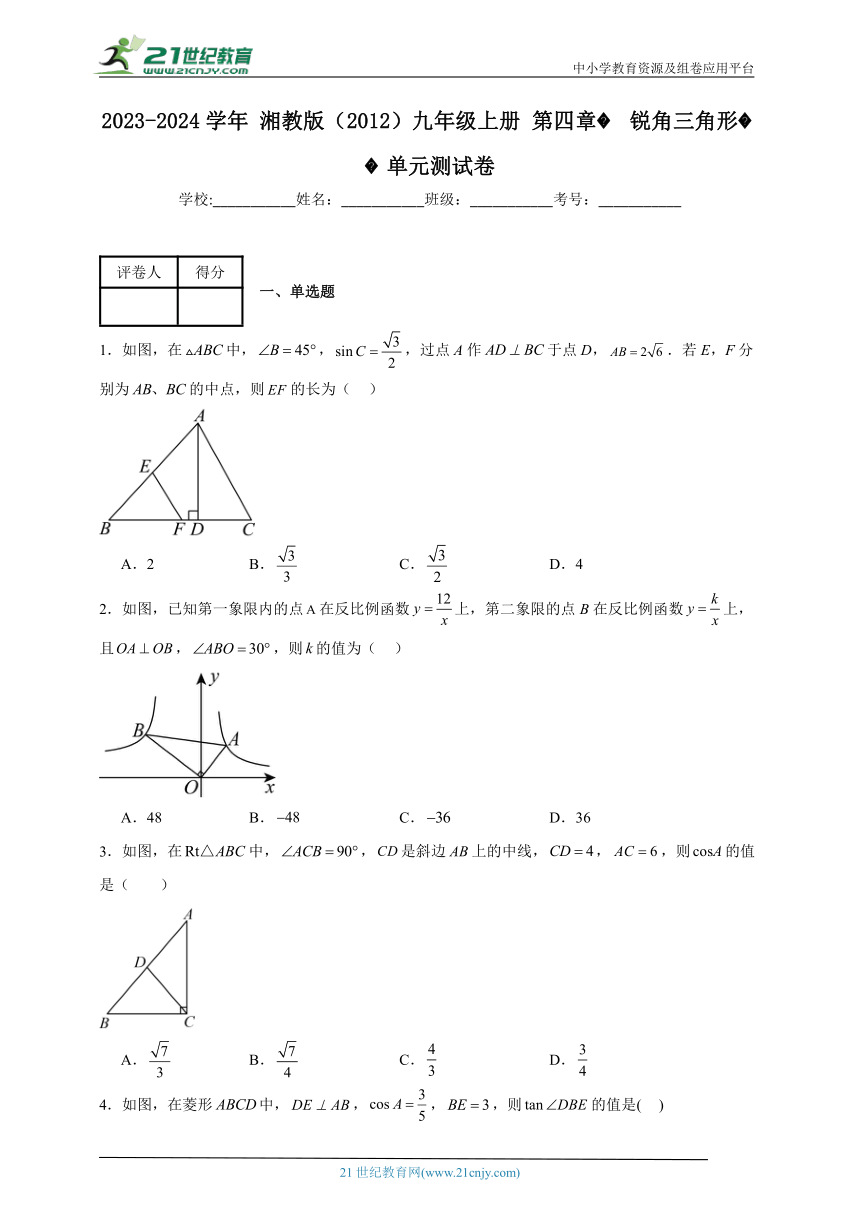
1．如图，在中，，，过点A作于点D，．若E，F分别为的中点，则的长为（ ）
A．2 B． C． D．4
2．如图，已知第一象限内的点在反比例函数上，第二象限的点B在反比例函数上，且，，则的值为（ ）

A．48 B． C． D．36
3．如图，在中，，是斜边上的中线，，，则的值是（　　）
A． B． C． D．
4．如图，在菱形中，，，，则的值是( )
A． B．2 C． D．
5．将正方体的一种展开图按如图方式放置在直角三角形纸片上，则的值等于（ ）

A． B． C． D．
6．在中，，，则，则（ ）
A．24 B．20 C．16 D．15
7．如图，在中，，的垂直平分线交于点D，交于点E，，则（ ）

A． B． C． D．
8．如图，菱形的边长为4，且于点为上一点，且的周长最小，则的周长的最小值为（ ）
A． B． C． D．
9．如图，在中，，，是上一点，若，则的长为（ ）．
A． B． C． D．
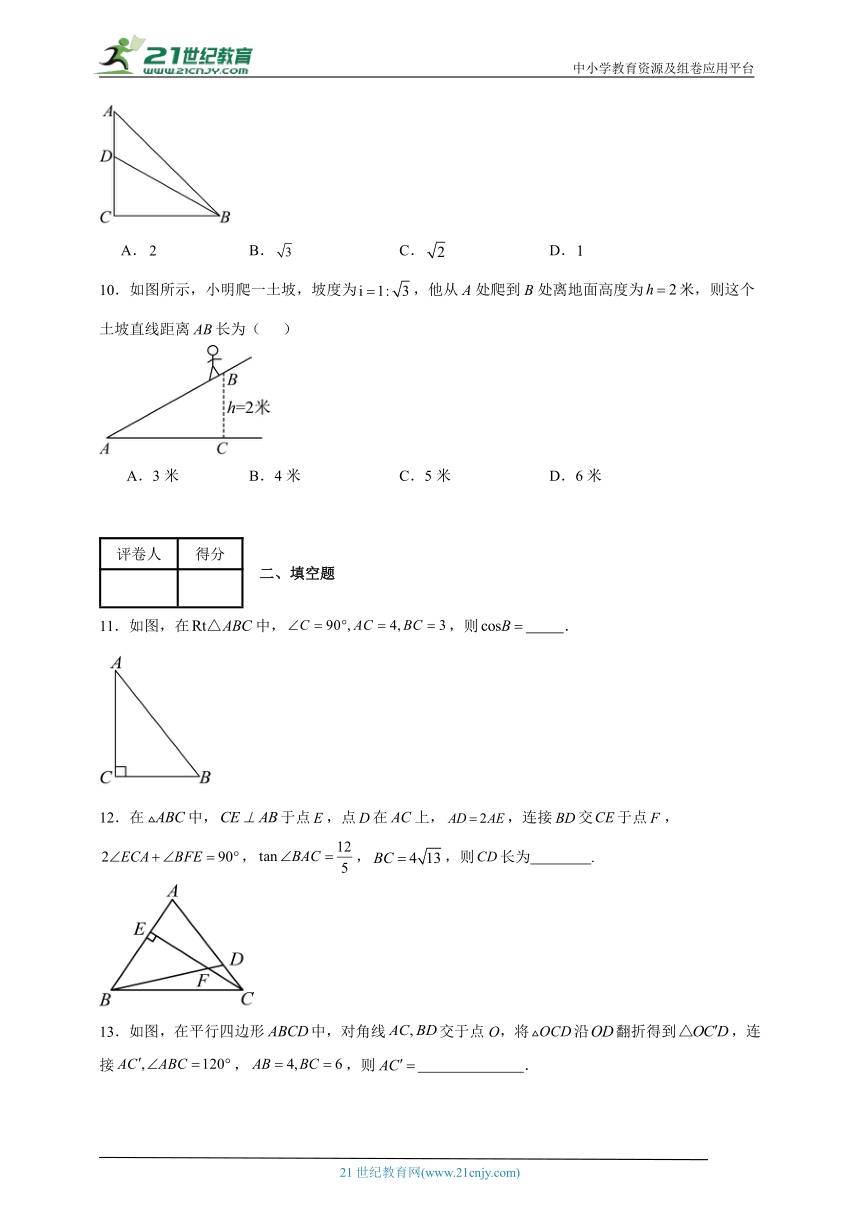
10．如图所示，小明爬一土坡，坡度为，他从A处爬到B处离地面高度为米，则这个土坡直线距离长为（ ）
A．3米 B．4米 C．5米 D．6米
评卷人得分
二、填空题
11．如图，在中，，则 ．
12．在中，于点，点在上，，连接交于点，，，，则长为 .
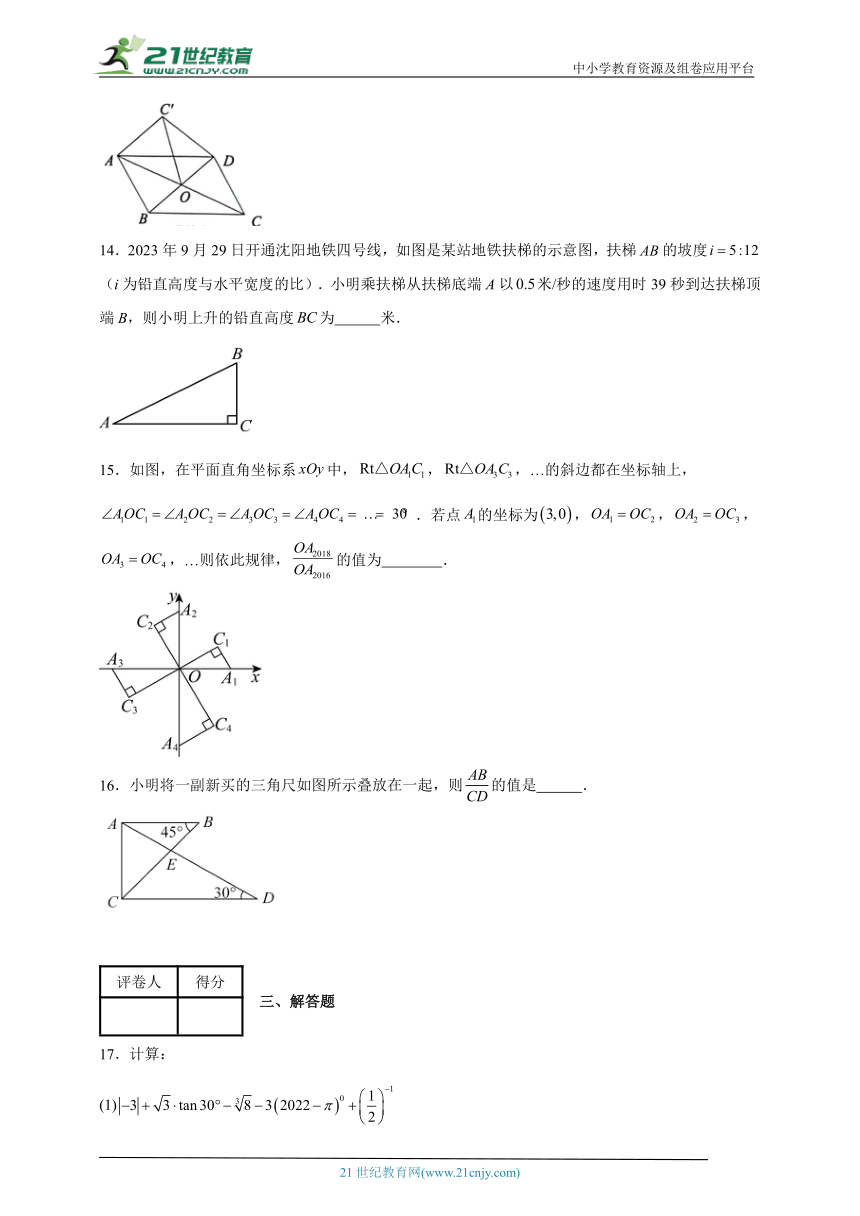
13．如图，在平行四边形中，对角线交于点O，将沿翻折得到，连接，，则 ．
14．2023年9月29日开通沈阳地铁四号线，如图是某站地铁扶梯的示意图，扶梯的坡度（i为铅直高度与水平宽度的比）．小明乘扶梯从扶梯底端A以米/秒的速度用时39秒到达扶梯顶端B，则小明上升的铅直高度为 米．
15．如图，在平面直角坐标系中，，，…的斜边都在坐标轴上，．若点的坐标为，，，，…则依此规律，的值为 ．
16．小明将一副新买的三角尺如图所示叠放在一起，则的值是 ．
评卷人得分
三、解答题
17．计算：
(1)
(2)解方程：．
(3)先化简，再求值：，其．
18．计算：
(1)；
(2)．
参考答案：
1．A
【分析】本题考查解直角三角形，三角形中位线定理，由等腰直角三角形的性质求出，由锐角的正弦求出，由三角形中位线定理求出．
【详解】解：，
是等腰直角三角形，
∴，
∵，
∴，
∵E，F分别为的中点，
∴是的中位线，
∴．
故选：A．
2．C
【分析】本题考查了反比例函数图象上点的坐标特征：反比例函数（k为常数，）的图象是双曲线，图象上的点的横纵坐标的积是定值k,即。也考查了相似三角形的判定与性质及特殊角的三角函数值．
作轴于点C，作轴于点D，如图，证明，利用相似三角形的性质得到，利用反比例函数k的几何意义得到，从而解绝对值方程得到满足条件的k的值．
【详解】解：作轴于点C，作轴于点D.
则，
则，
∵，
∴，
∴，
∴，
∴.
又∵，
∴，
∴.

3．D
【分析】此题考查了求锐角的余弦值以及直角三角形斜边上的中线性质，利用直角三角形斜边上的中线等于斜边的一半求出斜边长，然后求出的值即可．熟练掌握锐角三角函数值的求法是解本题的关键．
【详解】解：在中，，是斜边上的中线，
，
，
，
，
，
故选：D．
4．B
【分析】本题考查了解直角三角形中三角函数的应用，欲求的值，只需通过解直角三角形求得的值即可．
【详解】解：设菱形边长为，
，
，
，
，
，
，
，
，
．
故选：B．
5．D
【分析】本题考查的是求解锐角的正弦，本题先利用平行线的性质把转化到已知直角三角形中，从而可得答案．
【详解】解：如图，

∵，
∴，
在中，
设，
，
，
．
故选：D．
6．D
【分析】本题主要考查了正弦的性质，利用正弦的性质求值即可．理解正弦的性质是解题的关键．
【详解】在中，，
即，
解得：．
故选：D．
7．C
【分析】本题考查求角的正切值，线段垂直平分线的性质，根据中垂线的性质，得到，根据，设，则，勾股定理求出的长，再利用，进行求解即可．
【详解】解：∵的垂直平分线交于点D，
∴，
∵，
∴设，则，
∵，
∴，
∴；
故选C
8．B
【分析】首先确定出的周长的最小值就是的最小值，然后利用将军饮马问题的模型构造出的周长的最小值，再利用勾股定理求出，进而解决问题．
【详解】解：连接交于点，连接，，
四边形是菱形，
对角线所在直线是其一条对称轴，点，点关于直线对称，与是等边三角形，
，
，
是的中点，
，
的周长，
要求的周长的最小值可先求出的最小值即可，
而的最小值就是的长，
过点作，交的延长线于点，
四边形是菱形，
，
，
在中，
，，
在中，
，，
，
的周长的最小值为，
故选：B．
【点睛】本题考查轴对称最短路线问题，菱形的性质，勾股定理，特殊值的三角函数，掌握相关图形的性质和构造出最短路线是解题的关键．
9．A
【分析】本题考查了解直角三角形，在直角三角形中，由已知元素求未知元素的过程就是解直角三角形，也考查了等腰直角三角形的性质，作于，由，得，根据等腰直角三角形的性质得到 ，设则，，在中，利用的正切得到，然后由可计算出 ，再利用 ，进行计算即可，解题的关键是添加辅助线构造直角三角形，再利用三角函数求边长．
【详解】作于，如图，
∵，
∴，
∵，
∴，
∴，是等腰直角三角形，
∴，
在中，设，则，
则，
在中，，
∴，
∴，解得：，
∴，
故选：．
10．B
【分析】本题考查了坡度的定义与相关计算，属于基础题型，熟知概念是关键．设斜坡的水平宽度为x米，根据坡度的定义可求出x，再根据勾股定理求解即可．
【详解】解：设斜坡的水平宽度为x米，
根据题意，得，
解得，
∴米，
故选：B．
11．/0.6
【分析】本题考查了求余弦，勾股定理，先根据勾股定理求出的长，再根据锐角三角函数的定义解答，掌握三角函数的定义是解题的关键．
【详解】解：∵在中，，
∴，
∴，
故答案为：．
12．3
【分析】本题考查了全等三角形的性质与判定，勾股定理，已知正切求边长．在上截取，延长至，使得，连接，设，，则，根据，得出，证明，得出，，，进而证明得出，根据已知条件得出，证明得出，在中，勾股定理得出，进而得出，即可求解．
【详解】解：如图所示，在上截取，延长至，使得，连接，
∵，
∴设，，则，
∵，
∴，，
∵，
在和中，
，
∴，
∴，，，
∴，，
又∵，
∴，
∴，
∵，，
∴，
又∵，
∴，
∴，
即，
在和中，
，
∴，
∴，
∴，
在中，，
∴
∴
故答案为：3．
13．
【分析】连接，过点作交的延长线于点，设，交于点，过点作于点，根据题意求得的长，进而等面积法求得的长，解，进而根据，利用正弦相等，列出方程，解方程，即可求解．
【详解】解：如图所示，连接，过点作交的延长线于点，设，交于点，过点作于点，
∵在平行四边形中，对角线交于点O，
∴
∵将沿翻折得到，
∴，
∴是直角三角形；
∵，
∴
∴，
∴，
∴
∵平行四边形的面积
∴
∴
∴,
∴
∵
∴
∴
∴
即
解得：，
故答案为：．
【点睛】本题考查了平行四边形的性质，折叠的性质，勾股定理，解直角三角形，熟练掌握以上知识是解题的关键．
14．
【分析】本题考查坡度和勾股定理，由可得，设，，根据勾股定理求出，再根据长度求出k值，即可求解．
【详解】解：由题意知（米），
扶梯的坡度，
，
设，，
则，
，
（米），
故答案为：．
15．/
【分析】本题考查了规律型，点的坐标，坐标与图形性质，含30度的直角三角形三边的关系及三角函数．根据含30度的直角三角形三边的关系即可得到结论．
【详解】解：，
；
；
，
…，
，
∴．
故答案为 ：．
16．/
【分析】设，解，得出，解，得出，代入，计算即可求得答案．
本题考查了解直角三角形，锐角三角函数的定义，设，用含k的代数式表示出与是解题的关键．
【详解】解：设，
∵在中，，，
∴，
∵在中，，，
∴，
∴．
故答案为．
17．(1)1
(2)，
(3)，
【分析】本题考查解一元二次方程，二次根式的混合运算，分式的化简求值，掌握分式的混合运算法则，二次根式混合运算的法则及一元二次方程的求解方法是解题关键．
（1）根据绝对值的性质、二次根式的化简、特殊角的三角函数值、负整数次幂的意义进行计算即可；
（2）利用因式分解法求解即可；
（3）根据分式的混合运算法则把原式化简，，得，代入计算得到答案．
【详解】（1）解：原式
；
（2），
，
，，
，；
（3）
，
由，得，
原式．
18．(1)
(2)
【分析】本题考查了特殊角的三角函数值的混合运算、零次幂、负整数指数幂及绝对值：
（1）利用特殊角的三角函数值的混合运算法则即可求解；
（2）利用特殊角的三角函数值的混合运算、零次幂、负整数指数幂及绝对值的运算法则即可求解；
熟练掌握其运算法则是解题的关键．
【详解】（1）解：原式
．
（2）原式
．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)