角角边定理
图片预览



文档简介
课件19张PPT。三角形全等的判定
(角角边定理的应用)2007.04学习目标:
1.了解角角边定理的来源,明白它的特点,记住此定理,并会准确判断和运用.
2.会区别角边角定理,角角边定理(它们的最大特点是都是已知两角和一边)学习指导:
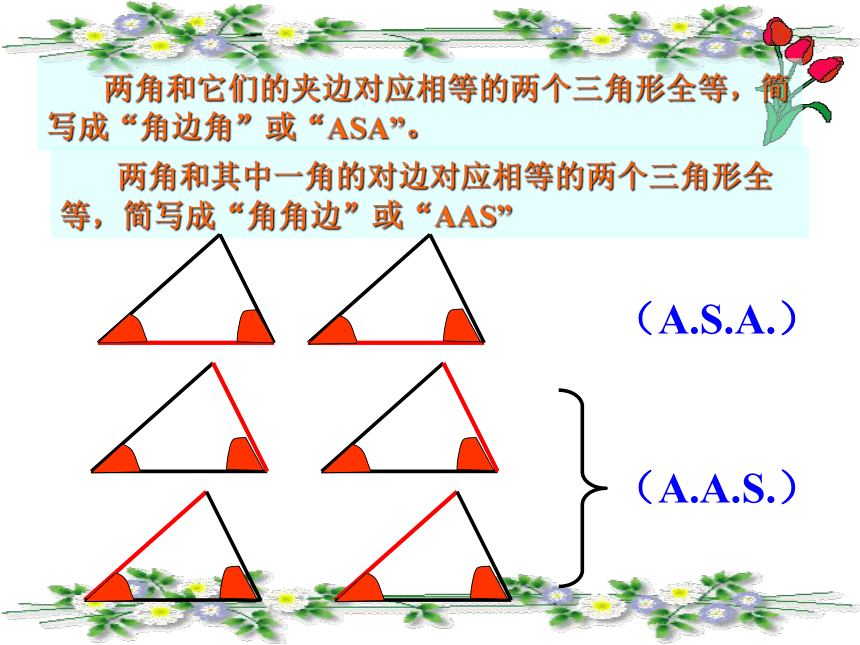
学习书本P73下思考与分析及P74上内容,了解角角边定理的来源和推理过程,并记住角角边定理,会区别它与角边角定理. 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”(A.S.A.)1、如图,已知AB=DE, ∠A =∠D, ,∠B=∠E,则
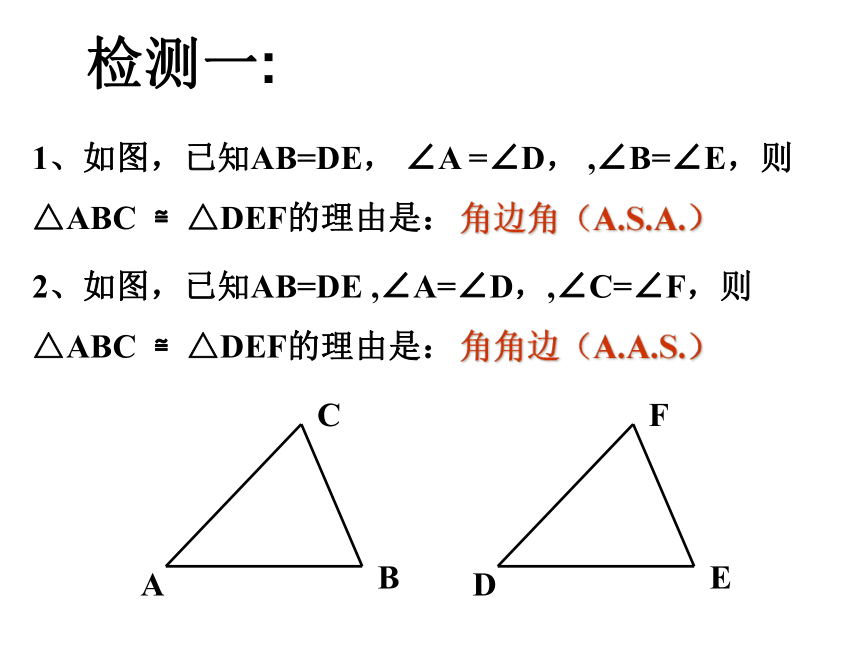
△ABC ≌△DEF的理由是:2、如图,已知AB=DE ,∠A=∠D,,∠C=∠F,则
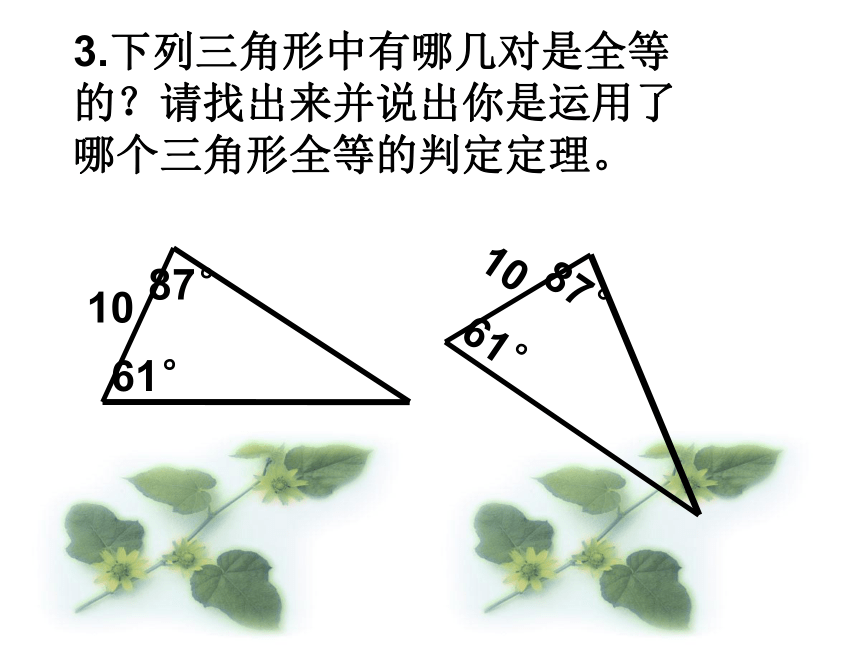
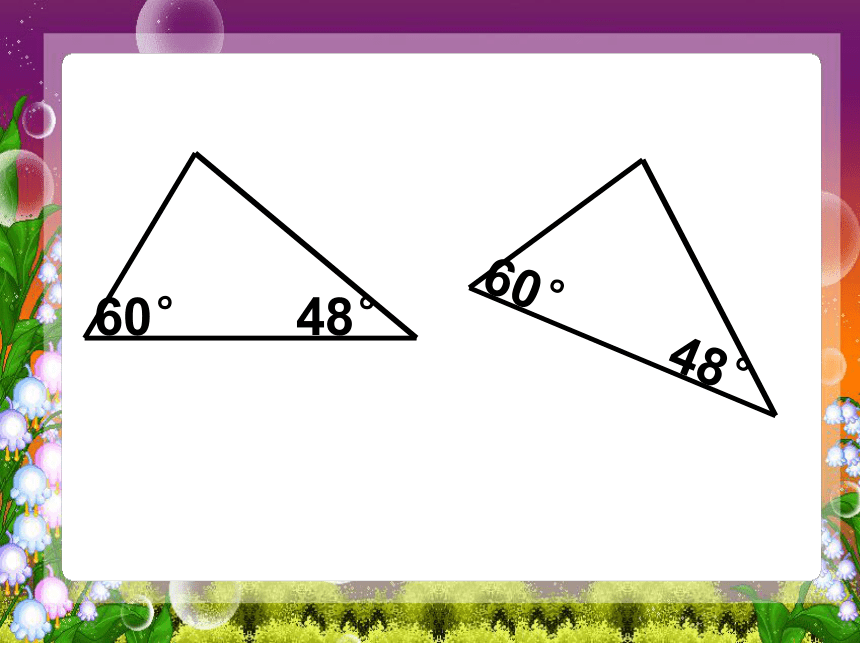
△ABC ≌△DEF的理由是:角边角(A.S.A.)角角边(A.A.S.)检测一:3.下列三角形中有哪几对是全等的?请找出来并说出你是运用了哪个三角形全等的判定定理。 4.已知:∠ACB= ∠DFE,BC=EF,那么
需要补充一个直接条件( )
才能使△ABC≌ △DEF (吉林省考)1、如图 ,AB=AC,∠B=∠C,那么△ABE 和△ACD全等吗?为什么?检测二:2、如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?3、如图,在△ABC 中 ,∠B=∠C,AD是∠BAC的
角平分线,那么AB=AC吗?为什么?检测三:
议一议 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?利用“角边角”可知,带B块去,可以配到一个与原来全等的三角形玻璃。AB议一议 今天我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另两个条件,它们分别是: 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“A.S.A.”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“A.A.S.”回顾总结:布置作业:P79 .5
P96 .6.
P97 .11如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?检测五: 思考题
(角角边定理的应用)2007.04学习目标:
1.了解角角边定理的来源,明白它的特点,记住此定理,并会准确判断和运用.
2.会区别角边角定理,角角边定理(它们的最大特点是都是已知两角和一边)学习指导:
学习书本P73下思考与分析及P74上内容,了解角角边定理的来源和推理过程,并记住角角边定理,会区别它与角边角定理. 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”(A.S.A.)1、如图,已知AB=DE, ∠A =∠D, ,∠B=∠E,则
△ABC ≌△DEF的理由是:2、如图,已知AB=DE ,∠A=∠D,,∠C=∠F,则
△ABC ≌△DEF的理由是:角边角(A.S.A.)角角边(A.A.S.)检测一:3.下列三角形中有哪几对是全等的?请找出来并说出你是运用了哪个三角形全等的判定定理。 4.已知:∠ACB= ∠DFE,BC=EF,那么
需要补充一个直接条件( )
才能使△ABC≌ △DEF (吉林省考)1、如图 ,AB=AC,∠B=∠C,那么△ABE 和△ACD全等吗?为什么?检测二:2、如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?3、如图,在△ABC 中 ,∠B=∠C,AD是∠BAC的
角平分线,那么AB=AC吗?为什么?检测三:
议一议 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?利用“角边角”可知,带B块去,可以配到一个与原来全等的三角形玻璃。AB议一议 今天我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另两个条件,它们分别是: 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“A.S.A.”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“A.A.S.”回顾总结:布置作业:P79 .5
P96 .6.
P97 .11如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?检测五: 思考题
