利用等式性质解一元一次方程

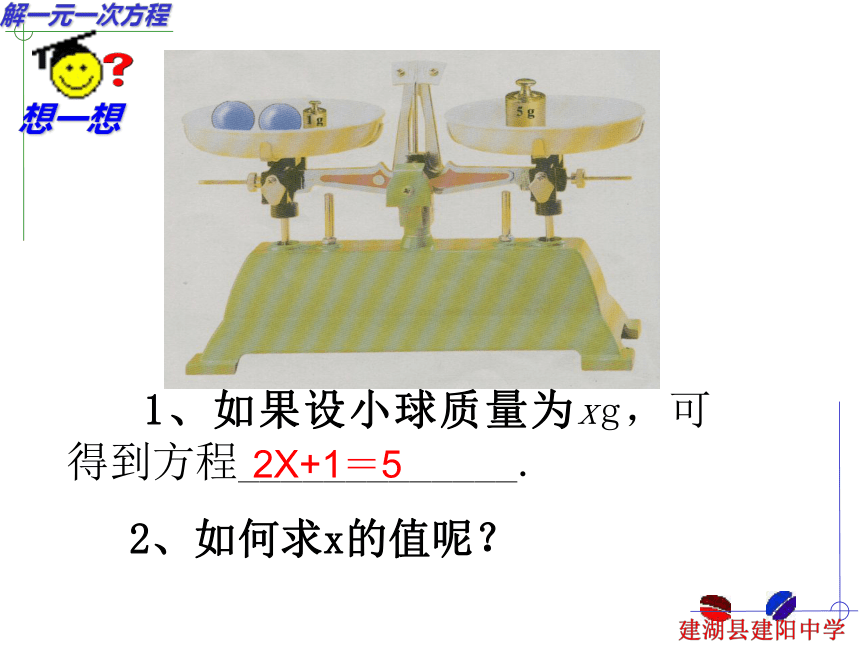
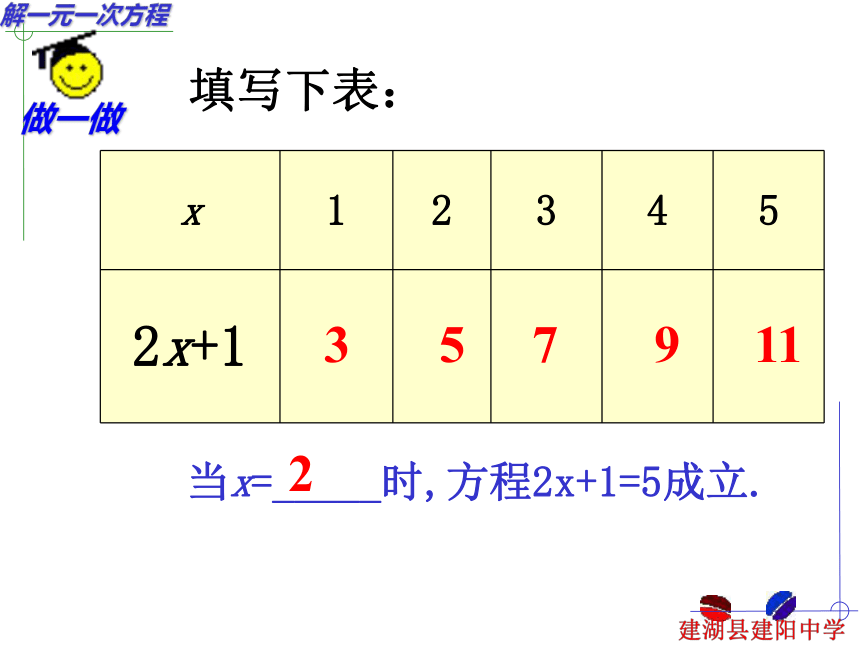
课件18张PPT。苏科版七年级数学4.2解一元一次方程 1、如果设小球质量为xg，可得到方程_____________.2X+1＝5 2、如何求x的值呢？填写下表：357911 当x=_____时,方程2x+1=5成立.2试一试 分别把0、1、2、3、4代入下列 方程，哪个值能使方程成立：
（1）2 x – 1 = 5
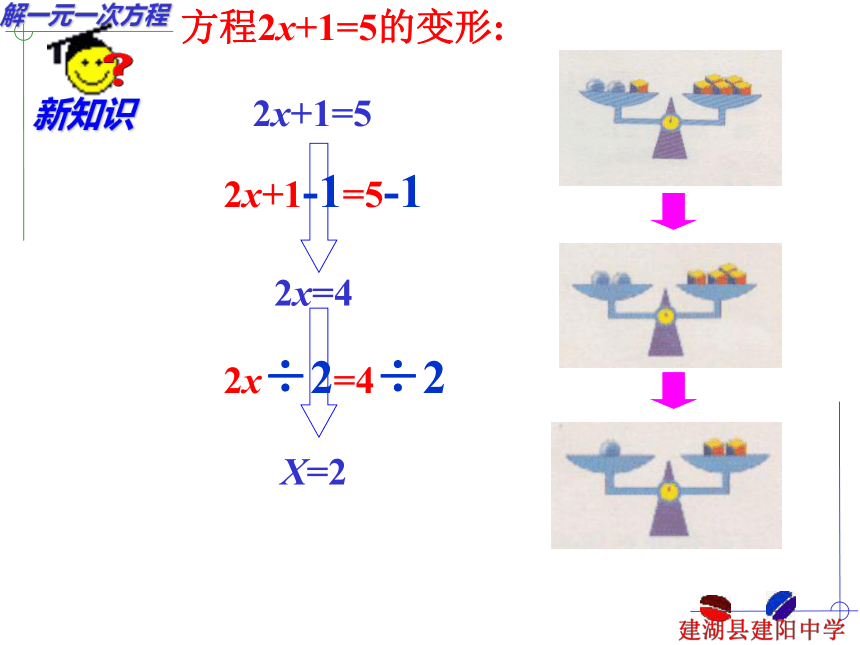
（2）3 x – 2 = 4 x – 331 能使方程左右两边相等的未知数的值叫方程的解. 求方程解的过程叫解方程.这两个概念的区别：方程的解 是使方程成立的未知数的值；而解方程是确定方程解的过程，是一个变形过程。方程2x+1=5的变形:2x+1=52x=42x+1-1=5-1X=22x÷2=4÷23x=3+2xx=33x-2x=3+2x-2x 等式两边都加上或减去同一个数或同一个整式，所得结果仍是等式。(等式性质1)
等式两边都乘或除以同一个不等于零的数，所得结果仍是等式。 (等式性质2)例1：解下列方程(1) x+5=2两边都减去5,得X+5-5=2-5合并同类项,得X=-3(等式性质1)解:(2) -2x=4解:两边都除以-2,得(等式性质2)即X=-2求方程解就是将方程变形为x=a解下列方程(1) x+2=-6(2) -3x=3-4x(4) -6x=2例2 ：解下列方程 4 x = –1 + 3 x并检验方程的解是否正确！解:(1)两边都减去3x，得
4x-3x=-1+3x-3x
合并同类项，得
x=-1
检验：
把x=-1代入方程4x=-1+3x中，
左边＝4×(-1)=-4，右边＝-1+3×(-1)=-4
因为左边＝右边，所以x=-1是方程的解。解 题 后 的 反 思1.你是怎么解的？每一步的依据是什么？还有其他解法吗？
2.怎样才叫做“方程解完了”？
3.使用等式的两个性质对方程两边进行“同加减”、“同乘除”的目的是什么？求方程的解就是将方程变形为x = a的形式 小 结：问题一：能这样解方程吗？下面的解法错在哪里？
解方程 4x = 2x
解: 方程两边都除以x , 得 4＝2
问题二：你能利用等式性质把“－1＝ x”变形为
“x ＝ －1 ”吗？练一练：1.用适当的数或整式填空，使所得结果仍为等式，并说明依据是什么？
（1）如果2＝5＋x , 那么x＝————
（2）如果6x＝5x－3 ，那么6x－ ＝ －3
（3）如果1/2y ＝ 4 , 那么y ＝ ————
12-35x8练一练：2.判断下列变形是否正确？
（1）由 x＋5 = y＋5 ，得 x = y （ ）
（2）由2x－1 = 4 ，得 2x = 5 （ ）
（3）由2x = 1 ，得 x = 2 （ ）
（4）由3x = 2x ，得 3= 2 （ ） √√××收获： 等式两边都加上或减去同一个数或同一个等式，所得结果仍是等式。(等式性质1） 等式两边都乘或除以同一个不等于零的数，所得结果仍是等式。 (等式性质2) 1：这节课我们利用天平原理得出了等式的两个性质，并初步学习了用等式的两个性质解一元一次方程。2：等式的性质：3.方程的解与解方程概念的区别：方程的解 是使方程成立的未知数的值；而解方程是确定方程解的过程，是一个变形过程。
4.所谓“一元一次方程解完了”，意味着经过对原方程的一系列变形(两边同加减、乘除)，最终把方程化为最简的形式： x = a
（即方程左边只一个未知数项，右边只有一个常数，且未知数项的系数是 1 。）
课后作业：
补充习题62—63第一课时做完!